Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems (Based on Quadratic Equations) Ex 6E
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6E.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6D
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6E
Question 1.
The distance by road between two towns A and B is 216 km., and by rail it is 208 km. A car travels at a speed of x km/hr. and the train travels at a speed which is 16 km/hr faster than the car. Calculate:
(i) the time taken by the car to reach town B from A, in terms of x ;
(ii) the time taken by the train, to reach town B from A, in terms of x.
(iii) If the train takes 2 hours less than the car, to reach town B, obtain an equation in x, and solve it.
(iv) Hence, find the speed of the train. [1998]
Solution:
Distance between two stations by road = 216 km and by rail = 208 km.
Speed of car = x km/hr.
and speed of train = (x + 16) km/ hr.
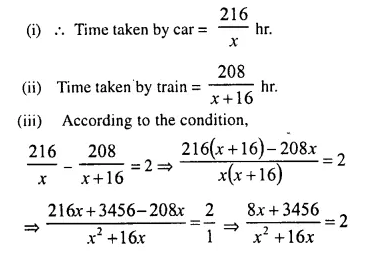
⇒ 8x + 3456 = 2×2 + 32x
⇒ 2x² + 32x – 8x – 3456 = 0
⇒ 2x² + 24x – 3456 = 0
⇒ x² + 12x – 1728 = 0 (Dividing by 2)
⇒ x² + 48x – 36x – 1728 = 0
⇒ x (x + 48) – 36 (x + 48) = 0
⇒ (x + 48 ) (x – 36) = 0
Either x + 48 =0, then x = – 48 which is not possible.
or x – 36 = 0, then x = 36
(iv) Speed of train = x + 16 = 36 + 16 = 52 km/hr.
Question 2.
A trader buys x articles for a total cost of Rs. 600.
(i) Write down the cost of one article in terms of x. If the cost per article were Rs. 5 more, the number of articles that can be bought for Rs. 600 would be four less.
(ii) Write down the equation in x for the above situation and solve it for x. [1999]
Solution:
C.P. of x articles = Rs. 600
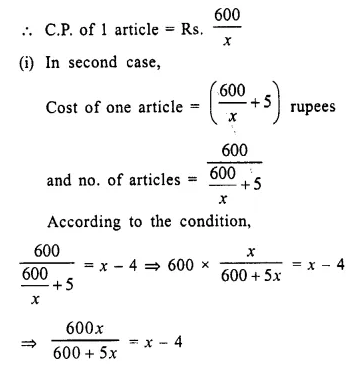
⇒ 600x = (x – 4) (600 + 5x) (By cross multiplication)
⇒ 600x = 600x + 5x² – 2400 – 20x
⇒ 5x² – 20x – 2400 = 0
(ii) x² – 4x – 480 = 0
⇒ x² – 24x + 20x – 480 = 0
⇒ x (x – 24) + 20 (x – 24) = 0
⇒ (x – 24) (x + 20) = 0 (Zero Product Rule)
Either x – 24 = 0, then x = 24
or x + 20 = 0, then x = -20 Which is not possible.
Hence no. of articles = 24
Question 3.
A hotel bill for a number of people for overnight stay is Rs. 4,800. If there were 4 people more, the bill each person had to pay would have reduced by Rs. 200. Find the number of people staying overnight. [2000]
Solution:
Amount of the bill = Rs. 4800
Let the number of persons staying overnight = x
Then amount to be paid by each person

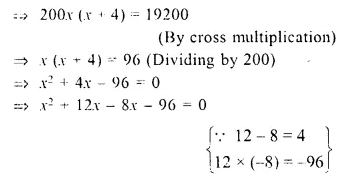
⇒ x (x + 12) – 8 (x + 12) = 0
⇒ (x + 12) (x – 8) = 0 (Zero Product Rule)
Either x + 12 = 0, then x = -12 which is not possible being negative
or x – 8 = 0, then x = 8
Hence no. of persons staying overnight = 8
Question 4.
An aeroplane travelled a distance of 400 km at an average speed of x km/hr. On the return journey, the speed was increased by 40 km/hr. Write down an expression lor the time taken for :
(i) the omvard journey;
(ii) the return journey.
If the return journey took 30 minutes less than the on ward journey, write down an equation in x and find its value. |2002]
Solution:
Distance between A and B = 400 km.
Speed of aeroplane onward journey = x km/hr.
and Speed of aeroplane on return journey = (x + 40) km/hr.
Now time taken for onward journey = \(\frac { 400 }{ x }\) hrs.
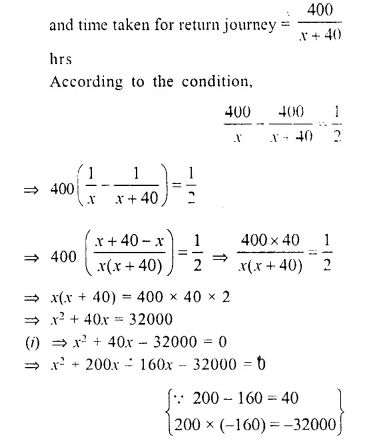
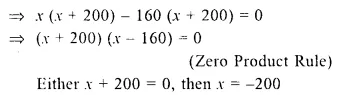
Which is not possible being negative
or x – 160 = 0, then x = 160
x = 160
Question 5.
Rs. 6,500 were divided equally among a certain number of persons. Had there been 15 persons more, each would have got Rs. 30 less. Find the original number of persons.
Solution:
Let original number of persons = x
Amount = Rs. 6,500

⇒ 30x² + 450x – 97500 = 0 (Dividing by 30)
⇒ x² + 15x – 3250 = 0
⇒ x² + 65x – 50x – 3250 = 0
⇒ x (x + 65) – 50 (x + 65) = 0
⇒ (x + 65) (x – 50) = 0
Either x + 65 = 0, then x = -65 which is not possible.
or x – 50 = 0, then x = 50
Original number of persons = 50
Question 6.
A plane left 30 minutes later than the scheduled time and in order to reach its destination 1500 km. away in time, it has to increase its speed by 250 km./hr. from its usual speed. Find its usual speed.
Solution:
Let the usual speed of plane = x km/hr.
Distance = 1500 km.
Increased speed = (x + 250) km./hr.
Now, according to the condition,
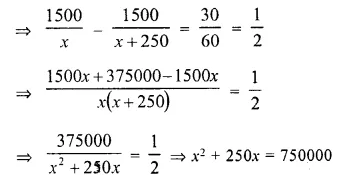
⇒ x² + 250x – 750000 = 0
⇒ x² + 1000x – 750x – 750000 = 0
⇒ x (x + 1000) – 750 (x + 1000) = 0
⇒ (x + 1000) (x – 750) = 0
Either x + 1000 = 0, then x = – 1000 But it is not possible.
or x – 750 = 0, then x = 750
Usual speed of plane = 750 km/hr
Question 7.
Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels 5 km/hr faster than the second train. If after 2 hours, they are 50 km apart, find the average speed of each train.
Solution:
Let the speed of first train = x km/hr.
Then speed of second train = (x – 5) km/ hr.
In 2 hours, first train will travel = 2x km.
and second train will travel = 2 (x – 5) km.
According to the condition,
2x + 2 (x – 5) = 50
⇒ 2x + 2x – 10 = 50
⇒ 4x = 50 + 10 = 60
x = 15 km/hr.
and speed of second train = 15 – 5 = 10 km/hr.
Question 8.
The sum S of first n even natural numbers is given by the relation S = n (n + 1). Find n if the sum is 420.
Solution:
S = n (n + 1) and x = 420
⇒ n (n + 1) = 420
⇒ n² + n – 420 = 0
⇒ n² + 21n – 20n – 420 = 0
⇒ n (n + 21) – 20 (n + 21) = 0
⇒ (n + 21) (n – 20) = 0
Either n + 21 =0, then n = -21 which is not possible as it is negative
or n – 20 = 0 then n = 20
Question 9.
The Sum of the ages of a father and his son is 45 years. Five year ago, the product of their ages (in years) was 124. Determine their present ages.
Solution:
Let age of father = x years
Then age of his son = (45 – x) years (sum = 45 years)
5 years ago,
The age of father = (x – 5) years
and age of son = 45 – x – 5 = (40 – x) years
According to the condition,
(x – 5) (40 – x) = 124
⇒ 40x – x² – 200 + 5x = 124
⇒ -x² + 45x – 200 – 124 = 0
⇒ -x² + 45x – 324 = 0
⇒ x² – 45x + 324 = 0
⇒ x² – 36x – 9x + 324 = 0
⇒ x (x – 36) – 9 (x – 36) = 0
⇒ (x – 36) (x – 9) = 0
Either x – 36 = 0, then x = 36
or x – 9 = 0, then x = 9, but it is not possible as age of father cannot be less than his son.
Age of father = 36 years
and age of son = 45 – 36 = 9 years
Question 10.
In an auditorium, seats were arranged in rows and columns. The number of rows w as equal to the number of seats in each row. When the number of rows was doubled and the number of seats in each row was reduced by 10, the total number of seats increased by 300. Find :
(i) the number of rows in the original arrangement.
(ii) the number of seats in the auditorium after re-arrangement. [2003]
Solution:
Let the number of rows in the auditorium = x
No. of seats in each row = x
and no. of total seats in the auditorium =
x x x = x²
In second case,
No. of rows = 2x
and no. of seats in each row = x – 10
Then the total seats will = x² + 300
Now, according to the condition,
2x (x – 10) = x² + 300
⇒ 2x² – 20x = x² + 300
⇒ 2x² – x² – 20x – 300 = 0
⇒ x² – 30x + 10x – 300 = 0
⇒ x (x – 30) + 10 (x – 30) = 0
⇒ (x – 30) (x + 10) = 0 (Zero Product Rule)
Either x – 30 = 0, then x = 30
or x + 10 = 0, then x = -10 Which not possible.
(i) No. of rows in original arrangement = 30
(ii) and no. of seats after re-arrangements = x² + 300 = (30)2 + 300 = 900 + 300 = 1200
Question 11.
Mohan takes 16 days less than Manoj to do a piece of work. If both working together can do it in 15 days, how many days will Mohan alone complete the work?
Solution:
Let time taken by Mohan = x days
Time taken by Manoj = (x + 16) days
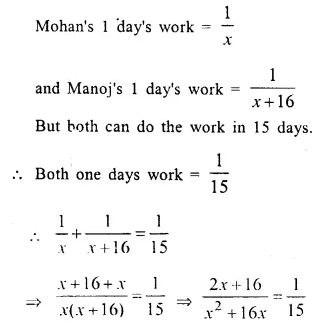
⇒ 30x + 240 = x² + 16x
⇒ x² + 16x – 30x – 240 = 0
⇒ x² – 14x – 240 = 0
⇒ x² – 24x + 10x – 240 = 0
⇒ x (x – 24) + 10 (x – 24) = 0
⇒ (x + 10) (x – 24) = 0
Either x + 10 = 0, then .x = -10 But it is not possible
or x – 24 = 0, then x = 24
Mohan can do the work in = 24 days
Question 12.
Two years ago. a man’s age was three times the square of his son’s age. In three years time, his age will be four times his son’s age. Find their present ages.
Solution:
2 years ago,
let son’s age = x
Man’s age = 3x
Son’s present age = x + 2
and man’s age = 3x² + 2
and 3 years after,
Son’s age = x + 2 + 3 = x + 5
Man’s age 3x² + 2 + 3 = 3x² + 5
According to condition,
3x² + 5 = 4 (x + 5)
⇒ 3x² + 5 = 4x + 20
⇒ 3x² – 4x + 5 – 20 = 0
⇒ 3x² – 4x – 15 = 0
⇒ 3x² – 9x + 5x – 15 = 0
⇒ 3x (x – 3) + 5 (x – 3) = 0
⇒ (x – 3) (3x + 5) = 0
Either x – 3 = 0, then x = 3
or 3x + 5 = 0, then 3x = -5 ⇒ x = \(\frac { -5 }{ 3 }\)
But it is not possible.
x = 3
Son’s present age = x + 2 = 3 + 2 = 5 years
and man’s present age = 3x² + 2 = 3(3)² + 2 = 27 + 2 = 29 years
Question 13.
In a certain positive fraction, the denominator is greater than the numerator by 3. If 1 is subtracted from the numerator and the denominator both. the fraction reduces by \(\frac { 1 }{ 14 }\) Find the fraction.
Solution:
In first case.
Let numerator of a fraction = x
then, its denominator = x + 3
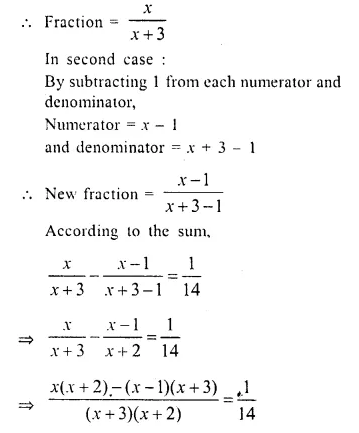
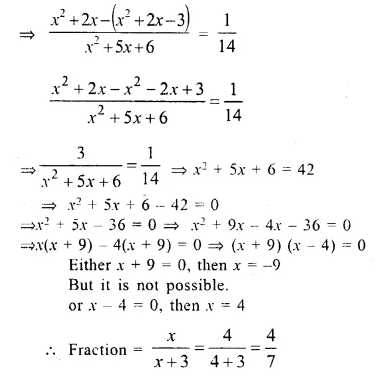
Question 14.
In a two digit number, the ten’s digit is bigger. The product of the digits is 27 and the difference between two digits is 6. Find the number.
Solution:
Difference of digits = 6
Let one’s digit = x
Then ten’s digit = x + 6
and number = x + 10 (x + 6) = x + 10x + 60 = 11x + 60
But product of digits = 27
x (x + 6) = 27
⇒ x² + 6x – 27 = 0
⇒ x² + 9x – 3x – 27 = 0
⇒ x (x + 9) – 3 (x + 9) = 0
⇒ (x + 9) (x – 3) = 0
Either x + 9 = 0, then x = – 9 But it is not possible
or x – 3 = 0, then x = 3
Number = 11x + 60 = 11 x 3 + 60 = 33 + 60 = 93
Question 15.
Some school children on an excursion by a bus to a picnic spot at a distance of 300 km. While returning, it was raining and the bus had to reduce its speed by 5 km/ hr and it took two hours longer for returning. Find the time taken to return.
Solution:
Distance = 300 km.
Let speed of the bus = x km/hr.
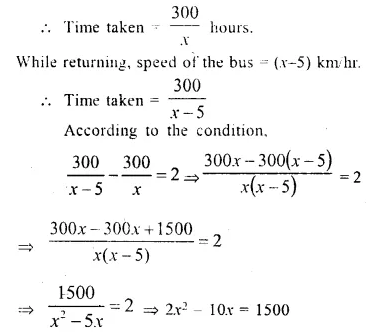
⇒ x² – 5x = 750
⇒ x² – 5x – 750 = 0
⇒ x² – 30x + 25x – 750 = 0
⇒ x (x – 30) + 25 (x – 30) = 0
⇒ (x – 30) (x + 25) = 0
Either x – 30 = 0, then x = 30
or x + 25 = 0, then x = -25, but it is not possible as it is negative
Speed of the bus = 30 km/hr
and time taken while returning = \(\frac { 300 }{ x }\) = \(\frac { 300 }{ 25 }\) = 12 hours
Question 16.
Rs. 480 is divided equally among ‘x’ children. If the number of children were 20 more then each would have got Rs. 12 less. Find ‘x’.
Solution:
Total amount = Rs. 480
Number of children = x
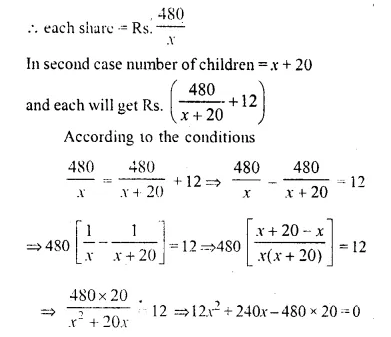
⇒ x² + 20x – 800 = 0
⇒ x² + 40x – 20x – 800 – 0
⇒ x (x + 40) – 20 (x + 40) = 0
⇒ (x + 40) (x – 20) = 0
Either x + 40 = 0, then x = – 40 which is not possible being negative
or x – 20 = 0 then x = 20
Number of children = 20
Question 17.
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain its speed gets reduced by 10 km/h and as such it takes two hrs longer to covers the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate ‘x’ (2016)
Solution:
Let the original speed be x km/hr
Time taken by the bus with moving at speed x km/h = \(\frac { 240 }{ x }\)
Time taken by the bus with moving at speed (x – 10) km/h = \(\frac { 240 }{ x – 10 }\)
According to the given condition,
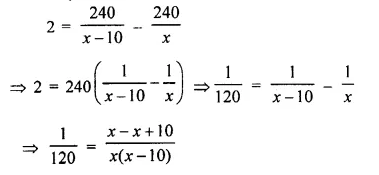
⇒ x (x – 10) = 10 x 120
⇒ x² – 10x = 1200
⇒ x² – 10x – 1200 = 0
⇒ x² – 40x + 30x – 1200 = 0
⇒ x (x – 40) + 30 (x – 40) = 0
⇒ (x – 40) (x + 30) = 0
⇒ x – 40 = 0 or x + 30 = 0
⇒ x = 40 or x = -30
Since, the speed cannot be negative, the uniform speed is 40 km/h
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 6 Solving Problems Ex 6E are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.