Surface Areas and Volumes Class 10 Notes Maths Chapter 13

On this page, you will find Surface Areas and Volumes Class 10 Notes Maths Chapter 13 Pdf free download. CBSE NCERT Class 10 Maths Notes Chapter 13 Surface Areas and Volumes will seemingly help them to revise the important concepts in less time.

CBSE Class 10 Maths Chapter 13 Notes Surface Areas and Volumes

Surface Areas and Volumes Class 10 Notes Understanding the Lesson

Surface area: Surface area of an object is the measure of the total area that the surface of an object occupies.

Volume: Volume of an object is the measure of space occupied by the object.

Basic Solids: In standard X, we have studied the surface area and volume of solids. Here we will study more about them.

1. Cuboid
(i) Surface area of cuboid = 2(lb + bh + lh) sq.unit
where l is the length
b is the breadth
h is the height

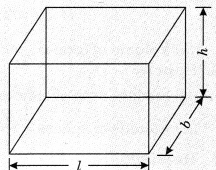
(ii) Area of four walls of cuboid
= 2(l + b) x h
= [Perimeter of floor x Height] sq. unit

(iii) Surface area of cuboid without roof or lid
= lb + 2 [bh + Ih] sq. unit

(iv) Volume of cuboid = l x b x h unit

(v) Diagonal of cuboid or length of longest rod kept =\(\sqrt{l^{2}+b^{2}+h^{2}}\)unit

2. Cube
Let each edge of a cube be of length a unit. Then
(i) Surface area of cube = 6 side² = 6a² unit

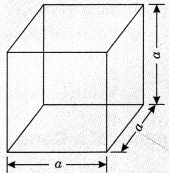
(ii) Surface area of four walls of cube = 4 side²
= 4a² sq. unit

(iii) Surface area of a cube without lid (or rod) of a cube
= 5a² sq. unit.

(iv) Length of longest diagonal (or rod) of a cube
\(=\sqrt{a^{2}+a^{2}+a^{2}}=\sqrt{3}\) aunit

(v) Volume of cube = a³ unit

3. Cylinder

(i) Curved surface area of cylinder = 2πr x h
= Perimeter of base x height sq. unit

(ii) Total surface area of cylinder
= CSA + Area of 2 circular ends of cylinder
= 2πrh + 2πr² = 2πr (r + h)

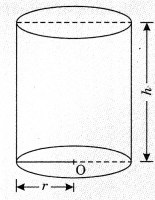
(iii) Volume of cylinder =πr²h

(iv) Volume of material in hollow pipe = Exterior volume – Interior volume
= πR²h – πr²h = πh [R² – r²]

(v) Total surface area of hollow cylinder
= CSA of outer and inner cylinder + 2(area of base ring)
= 2πRh + 2πrh + 2(πR² – πr²)
= 2π(R + r)h + 2π(R² – r²) = 2π(R + r) (h + R – r)

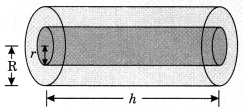
Note:

• Two ends of cylinder are circles having each area = πr²
• Mass of cylinder = Volume of cylinder x Density
  M = V x ρ

4. Cone

h – OA = height of cone
r = OB = radius of cone
l = AB = slant height of cone

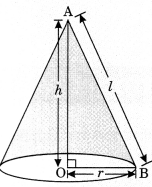
(i) \(l=\sqrt{r^{2}+h^{2}}\) units

(ii) Curved surface area of cone or lateral
surface area of cone = πrl sq. unit

(iii) Total surface area of cone = CSA + Area of circular base
= πrl + πr² – πr(r + l) sq. unit

(iv) Volume of cone =\( \frac{1}{3}\) πr²h cu.unit

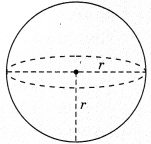
5. Sphere

• Surface area of sphere = 4πr² unit
• Volume of sphere = \( \frac{4}{3}\)cu.unit

6. Hemisphere

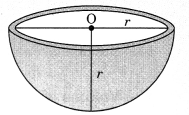
• Curved surface area of hemisphere = 4πr² sq unit
• Volume of hemisphere = \( \frac{2}{3}\) πr² cu unit
• Total surface area of hemisphere = 2πr² + πr² = 3πr² sq. unit

7. Spherical shell

(i) Total surface area of spherical shell = 4πR² + 4πr²
= 4πr(R² + r²) sq. unit

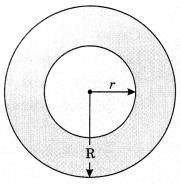
(ii) Volume of spherical shell = \( \frac{4}{3}\)π(R³– r³) cu . unit

Shapes of Frustum

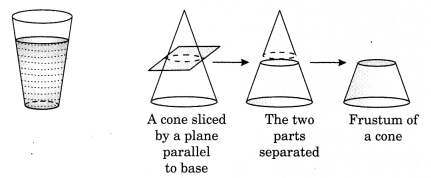
(i) Slant height of frustum = \(\sqrt{(\mathrm{R}-r)^{2}+h^{2}}\) unit
(ii) Curved surface area of frustum = π(R + r)l sq. unit
(iii) Total surface area of frustum of cone
= πl (R + r) + πR² + πr² sq. unit

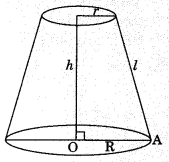
(iv) Volume of frustum of cone = \(\frac{1}{3}\)πh (R² + r² + Rr) sq. unit

Volume of Combination Solids

The volume of the solid formed by joining two basic solids will actually be the sum of the volumes of the two basic solids.

Conversion of Solid from One Shape to Another

If we melt the candle in the shape of cylinder and pour it into a conical vessel, then it changes into the conical shape. Thus, volume of cylindrical candle = Volume of conical solid.