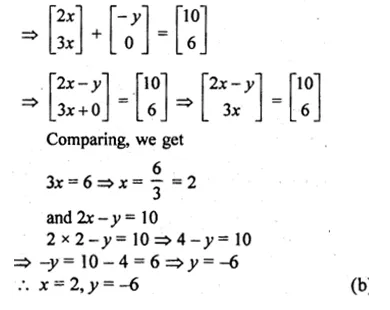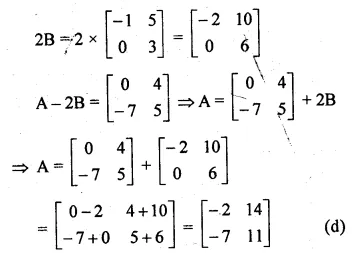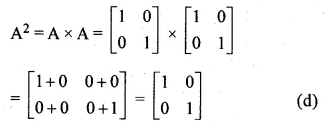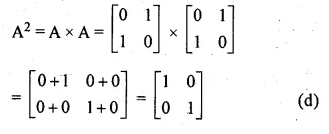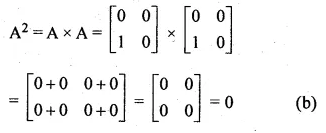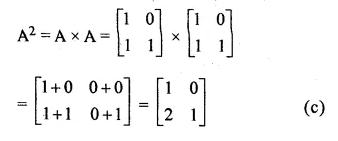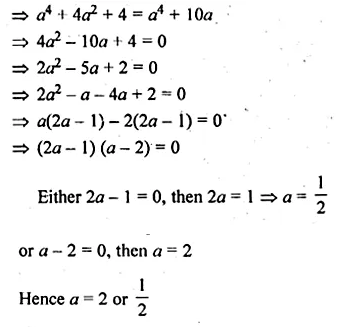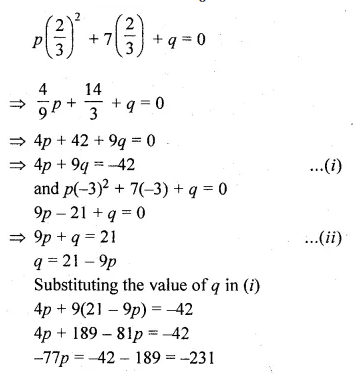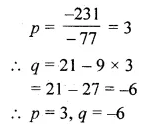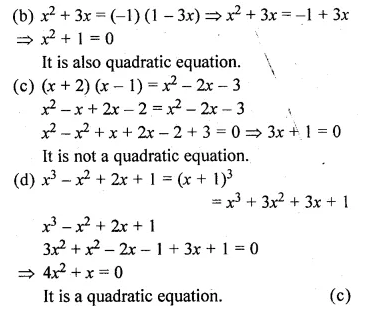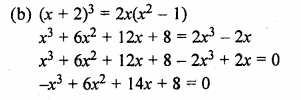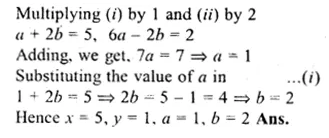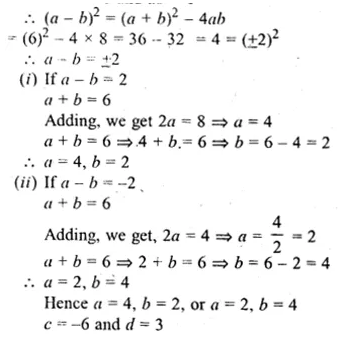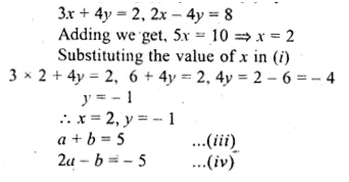Tag: APC Maths Class 10 Solutions ICSE

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Question 1.
Find the values of a and below
\(\begin{bmatrix} a+3 & { b }^{ 2 }+2 \\ 0 & -6 \end{bmatrix}=\begin{bmatrix} 2a+1 & 3b \\ 0 & { b }^{ 2 }-5b \end{bmatrix}\)
Solution:
\(\begin{bmatrix} a+3 & { b }^{ 2 }+2 \\ 0 & -6 \end{bmatrix}=\begin{bmatrix} 2a+1 & 3b \\ 0 & { b }^{ 2 }-5b \end{bmatrix}\)
comparing the corresponding elements
a + 3 = 2a + 1
⇒ 2a – a =3 – 1
⇒ a = 2
b² + 2 = 3b
⇒ b² – 3b + 2 = 0
⇒ b² – b – 2b + 2 = 0
⇒ b (b – 1) – 2 (b – 1) = 0
⇒ (b – 1) (b – 2) = 0.
Either b – 1 = 0, then b = 1
or b – 2 = 0, then b = 2
Hence a = 2, b = 2 or 1

Question 2.
Find a, b, c and d if \(3\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 4 & a+b \\ c+d & 3 \end{bmatrix}+\begin{bmatrix} a & 6 \\ -1 & 2d \end{bmatrix}\)
Solution:
Given
\(3\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 4 & a+b \\ c+d & 3 \end{bmatrix}+\begin{bmatrix} a & 6 \\ -1 & 2d \end{bmatrix}\)

Question 3.
Find X if Y = \(\begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix} \) and 2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \)
Solution:
Given
2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \)
⇒ 2X = 2X + Y = \(\begin{bmatrix} 1 & 0 \\ -3 & 2 \end{bmatrix} \) – Y

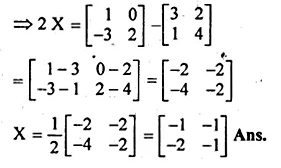
Question 4.
Determine the matrices A and B when
A + 2B = \(\begin{bmatrix} 1 & 2 \\ 6 & -3 \end{bmatrix} \) and 2A – B = \(\begin{bmatrix} 2 & -1 \\ 2 & -1 \end{bmatrix} \)
Solution:
A + 2B = \(\begin{bmatrix} 1 & 2 \\ 6 & -3 \end{bmatrix} \) …..(i)
2A – B = \(\begin{bmatrix} 2 & -1 \\ 2 & -1 \end{bmatrix} \) …….(ii)
Multiplying (i) by 1 and (ii) by 2

Question 5.
(i) Find the matrix B if A = \(\begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} \) and A² = A + 2B
(ii) If A = \(\begin{bmatrix} 1 & 2 \\ -3 & 4 \end{bmatrix} \), B = \(\begin{bmatrix} 0 & 1 \\ -2 & 5 \end{bmatrix} \)
and C = \(\begin{bmatrix} -2 & 0 \\ -1 & 1 \end{bmatrix} \) find A(4B – 3C)
Solution:
A = \(\begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} \)
let B = \(\begin{bmatrix} a & b \\ c & d \end{bmatrix} \)

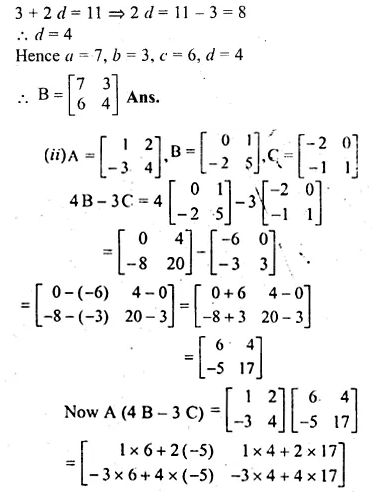
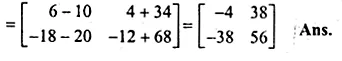
Question 6.
If A = \(\begin{bmatrix} 1 & 4 \\ 1 & 0 \end{bmatrix} \), B = \(\begin{bmatrix} 2 & 1 \\ 3 & -1 \end{bmatrix} \) and C = \(\begin{bmatrix} 2 & 3 \\ 0 & 5 \end{bmatrix} \) compute (AB)C = (CB)A ?
Solution:
Given
A = \(\begin{bmatrix} 1 & 4 \\ 1 & 0 \end{bmatrix} \),
B = \(\begin{bmatrix} 2 & 1 \\ 3 & -1 \end{bmatrix} \) and
C = \(\begin{bmatrix} 2 & 3 \\ 0 & 5 \end{bmatrix} \)

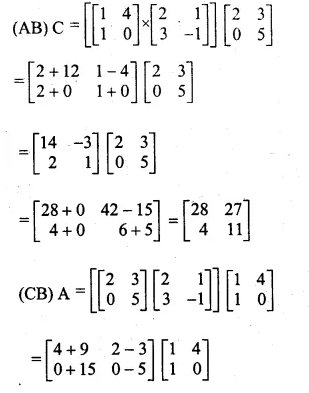
Question 7.
If A = \(\begin{bmatrix} 3 & 2 \\ 0 & 5 \end{bmatrix} \) and B = \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \) find the each of the following and state it they are equal:
(i) (A + B)(A – B)
(ii)A² – B²
Solution:
Given
A = \(\begin{bmatrix} 3 & 2 \\ 0 & 5 \end{bmatrix} \) and
B = \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \)

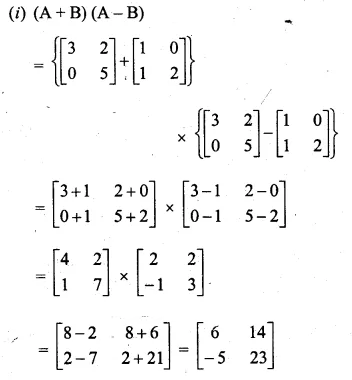
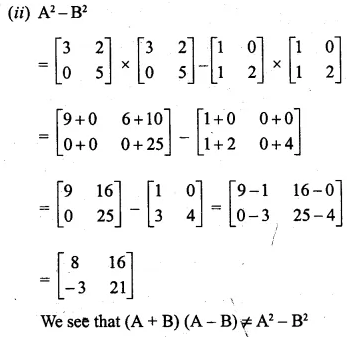
Question 8.
If A = \(\begin{bmatrix} 3 & -5 \\ -4 & 2 \end{bmatrix} \) find A² – 5A – 14I
Where I is unit matrix of order 2 x 2
Solution:
Given
A = \(\begin{bmatrix} 3 & -5 \\ -4 & 2 \end{bmatrix} \)

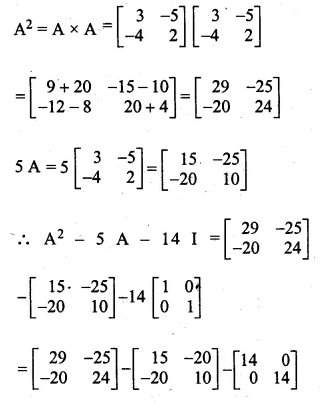
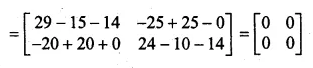
Question 9.
If A = \(\begin{bmatrix} 3 & 3 \\ p & q \end{bmatrix} \) and A² = 0 find p and q
Solution:
Given
A = \(\begin{bmatrix} 3 & 3 \\ p & q \end{bmatrix} \)

Question 10.
If A = \(\begin{bmatrix} \frac { 3 }{ 5 } & \frac { 2 }{ 5 } \\ x & y \end{bmatrix} \) and A² = I, find x,y
Solution:
Given
A = \(\begin{bmatrix} \frac { 3 }{ 5 } & \frac { 2 }{ 5 } \\ x & y \end{bmatrix} \)

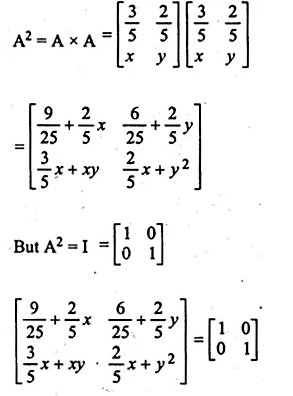
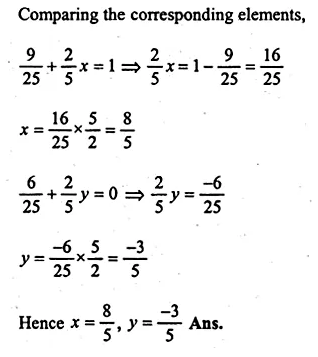
Question 11.
If \(\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \) find a,b,c and d
Solution:
Given
\(\begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix}\begin{bmatrix} a & b \\ c & d \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \)

Question 12.
Find a and b if
\(\begin{bmatrix} a-b & b-4 \\ b+4 & a-2 \end{bmatrix}\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}=\begin{bmatrix} -2 & -2 \\ 14 & 0 \end{bmatrix} \)
Solution:
Given
\(\begin{bmatrix} a-b & b-4 \\ b+4 & a-2 \end{bmatrix}\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}=\begin{bmatrix} -2 & -2 \\ 14 & 0 \end{bmatrix} \)

Question 13.
If A = \(\begin{bmatrix} { sec60 }^{ o } & { cos90 }^{ o } \\ { -3tan45 }^{ o } & { sin90 }^{ o } \end{bmatrix} \) and B = \(\begin{bmatrix} 0 & { cos45 }^{ o } \\ -2 & { 3sin90 }^{ o } \end{bmatrix} \)
Find (i) 2A – 3B (ii) A² (iii) BA
Solution:
Given
A = \(\begin{bmatrix} { sec60 }^{ o } & { cos90 }^{ o } \\ { -3tan45 }^{ o } & { sin90 }^{ o } \end{bmatrix} \) and
B = \(\begin{bmatrix} 0 & { cos45 }^{ o } \\ -2 & { 3sin90 }^{ o } \end{bmatrix} \)

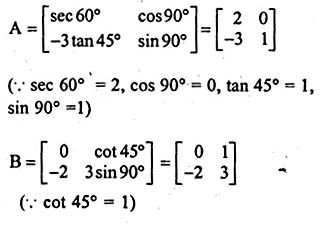
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Find the sum of:
(i) 20 terms of the series 2 + 6 + 18 + …
(ii) 10 terms of series 1 + √3 + 3 + …
(iii) 6 terms of the GP. 1, \(– \frac { 2 }{ 3 } \) , \(\\ \frac { 4 }{ 9 } \), …
(iv) 20 terms of the GP. 0.15, 0.015, 0.0015,…
(v) 100 terms of the series 0.7 + 0.07 + 0.007 +…
(vi) 5 terms and n terms of the series \(1+\frac { 2 }{ 3 } +\frac { 4 }{ 9 } +…\)
(vii) n terms of the G.P. √7, √21, 3√7, …
(viii)n terms of the G.P. 1, – a, a², – a³, … (a ≠ – 1)
(ix) n terms of the G.P. x³, x⁵ , x⁷, … (x ≠ ±1).
Solution:
(i) 2 + 6 + 18 + … 20 terms
Here, a = 2, r = 3, n = 20, r > 1

Question 2.
Find the sum of the first 10 terms of the geometric series
√2 + √6 + √18 + ….
Solution:
√2 + √6 + √18 + ….
Here, a = √2 , r = √3, r > 1

Question 3.
Find the sum of the series 81 – 27 + 9….\(– \frac { 1 }{ 27 } \)
Solution:
Given
81 – 27 + 9….\(– \frac { 1 }{ 27 } \)

Question 4.
The nth term of a G.P. is 128 and the sum of its n terms is 255. If its common ratio is 2, then find its first term.
Solution:
In a G.P.
T_n =128
S_n = 255
r = 2,
Let a be the first term, then

Question 5.
If the sum of first six terms of any G.P. is equal to 9 times the sum of the first three terms, then find the common ratio of the G.P.
Solution:
Sum of first 6 terms of a G.P. = 9 x The of first 3 terms
Let a be the first term and r be the common ratio

Question 6.
A G.P. consists of an even number of terms. If the sum of all the terms is 3 times the sum of the odd terms, then find its common ratio.
Solution:
Let the G.P. be a, ar, ar², … ar^{2n – 1}
These are 2n in number, which is an even number
A.T.Q.

Question 7.
(i) How many terms of the G.P. 3, 3², 3³, … are needed to give the sum 120?
(ii) How many terms of the G.P. 1, 4, 16, … must be taken to have their sum equal to 341?
Solution:
In G.P.
(i) 3, 3², 3³, …
Sum = 120, Here, a = 3, r = \(\frac { { 3 }^{ 2 } }{ 3 } \) = 3, r > 1

Question 8.
How many terms of the GP. 1, √2 > 2, 2 √2 , … are required to give a sum of 1023( √2 + 1)?
Solution:
GP. 1, √2 > 2, 2 √2 , …
Sum = 1023 (√2 + 1)
Here, a = 1, r = √2 . r > 1
Let number of terms be n, then

Question 9.
How many terms of the \(\frac { 2 }{ 9 } -\frac { 1 }{ 3 } +\frac { 1 }{ 2 } +…\) will make the sum \(\\ \frac { 55 }{ 72 } \) ?
Solution:
G.P. is \(\frac { 2 }{ 9 } -\frac { 1 }{ 3 } +\frac { 1 }{ 2 } +…\)
sum \(\\ \frac { 55 }{ 72 } \)

Question 10.
The 2nd and 5th terms of a geometric series are \(– \frac { 1 }{ 2 } \) and sum \(\\ \frac { 1 }{ 16 } \) respectively. Find the sum of the series upto 8 terms.
Solution:
In a G.P.
a₂ = \(– \frac { 1 }{ 2 } \) and a₅ = \(\\ \frac { 1 }{ 16 } \)
Let a be the first term and r be the common ratio

Question 11.
The first term of a G.P. is 27 and 8th term is \(\\ \frac { 1 }{ 81 } \) . Find the sum of its first 10 terms.
Solution:
In a G.P.
First term (a) = 27
a₈ = 81
Let r be the common ratio, then

Question 12.
Find the first term of the G.P. whose common ratio is 3, last term is 486 and the sum of whose terms is 728
Solution:
Common ratio of a G.P. = 3
and last term = 486
and sum of terms = 728

Question 13.
In a G.P. the first term is 7, the last term is 448, and the sum is 889. Find the common ratio.
Solution:
In a GP.
First term (a) = 7, last term (l) = 448
and sum = 889
Let r be the common ratio, then

Question 14.
Find the third term of a G.P. whose common ratio is 3 and the sum of whose first seven terms is 2186.
Solution:
In a G.P.
Common ratio = 3

Question 15.
If the first term of a G.P. is 5 and the sum of first three terms is \(\\ \frac { 31 }{ 5 } \), find the common ratio.
Solution:
In a G.P.
First term (a) = 5

Question 16.
The sum of first three terms of a GP. is to the sum of first six terms as 125 : 152. Find the common ratio of the GP.
Solution:
S₃ ÷ S₆ = 125 : 152
Let r be the common ratio and a be the first number, then

Question 17.
Find the sum of the products of the corresponding terms of the geometric progression 2, 4, 8, 16, 32 and 128, 32, 8, 2, \(\\ \frac { 1 }{ 2 } \)
Solution:
Sum of the product of corresponding terms of the G.M.s

Question 18.
Evaluate \(\sum _{ n=1 }^{ 50 }{ \left( { 2 }^{ n }-1 \right) } \)
Solution:
\(\sum _{ n=1 }^{ 50 }{ \left( { 2 }^{ n }-1 \right) } \)
Here n = 1, 2, 3,….,50

Question 19.
Find the sum of n terms of a series whose mth term is 2^m + 2m.
Solution:
a_m = 2^m + 2m
a₁ = 2¹ + 2 x 1 = 2 + 2

Question 20.
Sum the series
x(x + y) + x² (x² + y²) + x³ (x³ + y³) … to n terms.
Solution:
Given
S_n = x(x + y) + x² (x² + y²) + x³ (x³ + y³) … n terms

Question 21.
Find the sum of the series
1 + (1 + x) + (1 + x + x²) + … to n terms, x ≠ 1.
Solution:
1 + (1 + x) + (1 + x + x²) +… n terms, x ≠ 1
Multiply and divide by (1 – x)

Question 22.
Find the sum of the following series to n terms:
(i) 7 + 77 + 777 + …
(ii) 8 + 88 + 888 + …
(iii) 0.5 + 0.55 + 0.555 + …
Solution:
(i) 7 + 77 + 777 + … n terms
= 7[1 + 11 + 111 + … n terms]

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test.

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

Question 1.
The point P (4, – 7) on reflection in x-axis is mapped onto P’. Then P’ on reflection in the y-axis is mapped onto P”. Find the co-ordinates of P’ and P”. Write down a single transformation that maps P onto P”.
Solution:
P’ is the image of P (4, -7) reflected in x-axis
∴ Co-ordinates of P’ are (4, 7)
Again P” is the image of P’ reflected in y-axis
∴ Co-ordinates of P” are (-4, 7)
∴ Single transformation that maps P and P” is in the origin.

Question 2.
The point P (a, b) is first reflected in the origin and then reflected in the y-axis to P’. If P’ has co-ordinates (3, – 4), evaluate a, b
Solution:
The co-ordinates of image of P(a, b) reflected in origin are (-a, -b).
Again the co-ordinates of P’, image of the above point (-a, -b)
reflected in the y-axis are (a, -b).
But co-ordinates of P’ are (3, -4)
∴a = 3 and -b = -4
b = 4 Hence a = 3, b = 4.

Question 3.
A point P (a, b) becomes ( – 2, c) after reflection in the x-axis, and P becomes (d, 5) after reflection in the origin. Find the values of a, b, c and d.
Solution:
If the image of P (a, b) after reflected in the x-axis be (a, -b) but it Is given (-2, c).
a = -2, c = -b
If P is reflected in the origin, then its co-ordinates will be (-a, -b), but it is given (d, 5)
∴ -b = 5 ⇒ b = -5
d = -a = -(-2) = 2, c = -b = -(-5) = 5
Hence a = -2, b = -5, c = 5, d = 2

Question 4.
A (4, – 1), B (0, 7) and C ( – 2, 5) are the vertices of a triangle. ∆ ABC is reflected in the y-axis and then reflected in the origin. Find the co-ordinates of the final images of the vertices.
Solution:
A (4, -1), B (0, 7) and C (-2, 5) are the vertices of ∆ABC.
After reflecting in y-axis, the co-ordinates of points will be
A’ (-4, -1), B’ (0, 7), C’ (2, 5). Again reflecting in origin,
the co-ordinates of the images of the vertices will be
A” (4, 1), B” (0, -7), C” (-2, -5)

Question 5.
The points A (4, – 11), B (5, 3), C (2, 15), and D (1, 1) are the vertices of a parallelogram. If the parallelogram is reflected in the y-axis and then in the origin, find the co-ordinates of the final images. Check whether it remains a parallelogram. Write down a single transformation that brings the above change.
Solution:
The points A (4, -11), B (5, 3), C (2, 15) and D (1, 1) are the vertices of a parallelogram.
After reflecting in/-axis, the images of these points will be
A’ ( -4, 11), B’ (-5, 3), C (-2, 15) and D’ (-1, 1).
Again reflecting these points in origin, the image of these points will be
A” (4, -11), B” (5, -3), C” (2, -15), D” (0, -1)
Yes, the reflection of a single transformation is in the x-axis.

Question 6.
Use a graph paper for this question (take 2 cm = 1 unit on both x and y axes).
(i) Plot the following points:
A (0, 4), B (2, 3), C (1, 1) and D (2, 0).
(ii) Reflect points B, C, D on 7-axis and write down their coordinates. Name the images as B’, C’, D’ respectively.
(iii) Join points A, B, C, D, D’, C’, B’ and A in order, so as to form a closed figure. Write down the equation of line of symmetry of the figure formed. (2017)
Solution:
(i) On graph A (0, 4), B (2, 3), C (1, 1) and D (2, 0)
(ii) B’ = (-2, 3), C’ = (-1, 1), D’ = (-2, 0)

The equation of the line of symmetry is x = 0

Question 7.
The triangle OAB is reflected in the origin O to triangle OA’B’. A’ and B’ have coordinates ( – 3, – 4) and (0, – 5) respectively.
(i) Find the co-ordinates of A and B.
(ii) Draw a diagram to represent the given information.
(iii) What kind of figure is the quadrilateral ABA’B’?
(iv) Find the coordinates of A”, the reflection of A in the origin followed by reflection in the y-axis.
(v) Find the co-ordinates of B”, the reflection of B in the x-axis followed by reflection in the origin.
Solution:
∆ OAB is reflected in the origin O to ∆ OA’B’,
Co-ordinates of A’ = (-3, -4), B’ (0, -5).
.’. Co-ordinates of A will be (3, 4) and of B will be (0, 5).
(ii) The diagram representing the given information has been drawn here.
(iii) The figure in the diagram is a rectangle.
(iv) The co-ordinates of B’, the reflection of B is the x-axis is (0, -5)
and co-ordinates of B”, the reflection in origin of the point (0, -5) will be (0, 5).
(v) The co-ordinates of the points, the reflection of A in the origin are (-3, -4)
and coordinates of A”, the reflected in y-axis of the point (-3, – 4) are (3, -4)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Choose the correct answer from the given four options (1 to 14) :

Question 1.
If A = [a_ij]_2×2 where a_ij = i + j, then A is equal to
(a) \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \)
(b) \(\begin{bmatrix} 2 & 3 \\ 3 & 4 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 2 \\ 1 & 2 \end{bmatrix} \)
(d) \(\begin{bmatrix} 1 & 1 \\ 2 & 2 \end{bmatrix} \)
Solution:
A = [a_ij]_2×2 where a_ij = i + j, then A is equal to
\(\begin{bmatrix} 2 & 3 \\ 3 & 4 \end{bmatrix} \) (b)

Question 2.
If \(\begin{bmatrix} x+3 & 4 \\ y-4 & x+y \end{bmatrix}=\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \) then the values of x and y are
(a) x = 2, y = 7
(b) x = 7, y = 2
(c) x = 3, y = 6
(d) x = – 2, y = 7
Solution:
\(\begin{bmatrix} x+3 & 4 \\ y-4 & x+y \end{bmatrix}=\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \)
Comparing we get
x + 3 = 5
⇒ x = 5 – 3 = 2
and y – 4 = 3
⇒ y = 3 + 4 = 7
x = 2, y = 7 (a)

Question 3.
If \(\begin{bmatrix} x+2y & -y \\ 3x & 7 \end{bmatrix}=\begin{bmatrix} -4 & 3 \\ 6 & 4 \end{bmatrix} \) then the values of x and y are
(a) x = 2, y = 3
(b) x = 2, y = – 3
(c) x = – 2, y = 3
(d) x = 3, y = 2
Solution:
\(\begin{bmatrix} x+2y & -y \\ 3x & 7 \end{bmatrix}=\begin{bmatrix} -4 & 3 \\ 6 & 4 \end{bmatrix} \)
Comparing, we get
3x = 6
⇒ \(x= \frac { 6 }{ 3 } \) = 2
⇒ -y = 3
⇒ y = – 3
x = 2, y = -3 (b)

Question 4.
If \(\begin{bmatrix} x-2y & 5 \\ 3 & y \end{bmatrix}=\begin{bmatrix} 6 & 5 \\ 3 & -2 \end{bmatrix} \) then the value of x is
(a) – 2
(b) 0
(c) 1
(d) 2
Solution:
\(\begin{bmatrix} x-2y & 5 \\ 3 & y \end{bmatrix}=\begin{bmatrix} 6 & 5 \\ 3 & -2 \end{bmatrix} \)
Comparing, we get
y = -2
and x – 2y = 6
⇒ x – 2 x (-2) = 6
⇒ x + 4 = 6
⇒ x = 6 – 4 = 2 (d)

Question 5.
If \(\begin{bmatrix} x+2y & 3y \\ 4x & 2 \end{bmatrix}=\begin{bmatrix} 0 & -3 \\ 8 & 2 \end{bmatrix} \) then the value of x – y is
(a) – 3
(b) 1
(c) 3
(d) 5
Solution:
\(\begin{bmatrix} x+2y & 3y \\ 4x & 2 \end{bmatrix}=\begin{bmatrix} 0 & -3 \\ 8 & 2 \end{bmatrix} \)
Comparing, we get
3y = -3
⇒ \(y= \frac { -3 }{ 3 } \) = -1
4x = 8
⇒ \(x= \frac { 8 }{ 4 } \) = 2
x – y = 2 – (-1) = 2 + 1 = 3 (c)

Question 6.
If \(x\left[ \begin{matrix} 2 \\ 3 \end{matrix} \right] +y\left[ \begin{matrix} -1 \\ 0 \end{matrix} \right] =\left[ \begin{matrix} 10 \\ 6 \end{matrix} \right] \) then the values of x and y are
(a) x = 2, y = 6
(b) x = 2, y = – 6
(c) x = 3, y = – 4
(d) x = 3, y = – 6
Solution:
Given
\(x\left[ \begin{matrix} 2 \\ 3 \end{matrix} \right] +y\left[ \begin{matrix} -1 \\ 0 \end{matrix} \right] =\left[ \begin{matrix} 10 \\ 6 \end{matrix} \right] \)

Question 7.
If B = \(\begin{bmatrix} -1 & 5 \\ 0 & 3 \end{bmatrix} \) and A – 2B = \(\begin{bmatrix} 0 & 4 \\ -7 & 5 \end{bmatrix} \)
then the matrix A is equal to
(a) \(\begin{bmatrix} 2 & 14 \\ -7 & 11 \end{bmatrix} \)
(b) \(\begin{bmatrix} -2 & 14 \\ 7 & 11 \end{bmatrix} \)
(c) \(\begin{bmatrix} 2 & -14 \\ 7 & 11 \end{bmatrix} \)
(d) \(\begin{bmatrix} -2 & 14 \\ -7 & 11 \end{bmatrix} \)
Solution:
Given
B = \(\begin{bmatrix} -1 & 5 \\ 0 & 3 \end{bmatrix} \) and
A – 2B = \(\begin{bmatrix} 0 & 4 \\ -7 & 5 \end{bmatrix} \)

Question 8.
If A + B = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \) and A – 2B = \(\begin{bmatrix} -1 & 1 \\ 0 & -1 \end{bmatrix} \)
then A is equal to
(a) \(\frac { 1 }{ 3 } \begin{bmatrix} 1 & 1 \\ 2 & 1 \end{bmatrix} \)
(b) \(\frac { 1 }{ 3 } \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 1 \\ 2 & 1 \end{bmatrix} \)
(d) \(\begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \)
Solution:
A + B = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \) and
A – 2B = \(\begin{bmatrix} -1 & 1 \\ 0 & -1 \end{bmatrix} \)

Question 9.
A = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \) then A² =
(a) \(\begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix} \)
(b) \(\begin{bmatrix} 0 & 0 \\ 1 & 1 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)
(d) \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)
Solution:
Given
A = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)

Question 10.
If A = \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \) , then A² =
(a) \(\begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix} \)
(b) \(\begin{bmatrix} 0 & 0 \\ 1 & 1 \end{bmatrix} \)
(c) \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)
(d) \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)
Solution:
Given
A = \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)

Question 11.
If A = \(\begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} \) , then A² =
(a) A
(b) O
(c) I
(d) 2A
Solution:
Given
A = \(\begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} \)

Question 12.
If A = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \) , then A² =
(a) \(\begin{bmatrix} 2 & 0 \\ 1 & 1 \end{bmatrix} \)
(b) \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 0 \\ 2 & 1 \end{bmatrix} \)
(d) none of these
Solution:
Given
A = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \)

Question 13.
If A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \) , then A² =
(a) \(\begin{bmatrix} 8 & 5 \\ -5 & 3 \end{bmatrix} \)
(b) \(\begin{bmatrix} 8 & -5 \\ 5 & 3 \end{bmatrix} \)
(c) \(\begin{bmatrix} 8 & -5 \\ -5 & -3 \end{bmatrix} \)
(d) \(\begin{bmatrix} 8 & -5 \\ -5 & 3 \end{bmatrix} \)
Solution:
A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \)
A² = A x A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \)\(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \)

Question 14.
If A = \(\begin{bmatrix} 2 & -2 \\ -2 & 2 \end{bmatrix} \) , then A² = pA, then the value of p is
(a) 2
(b) 4
(c) – 2
(d) – 4
Solution:
A = \(\begin{bmatrix} 2 & -2 \\ -2 & 2 \end{bmatrix} \)
and A² = pA

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

Choose the correct answer from the given four options (1 to 7) :

Question 1.
The reflection of the point P ( – 2, 3) in the x-axis is
(a) (2, 3)
(b) (2, – 3)
(c) ( – 2, – 3)
(d) ( – 2, 3)
Solution:
Reflection of the point P (-2, 3) in x-axis is (-2, -3) (c)

Question 2.
The reflection of the point P ( – 2, 3) in the y- axis is
(a) (2, 3)
(b) (2, – 3)
(c) ( – 2, – 3)
(d) (0, 3)
Solution:
The reflection of the point P (-2, 3) under reflection in y-axis (2, 3) (a)

Question 3.
If the image of the point P under reflection in the x-axis is ( – 3, 2), then the coordinates of the point P are
(a) (3, 2)
(b) ( – 3, – 2)
(c) (3, – 2)
(d) ( – 3, 0)
Solution:
The image of the point P under reflection in the x-axis is (-3, 2),
then the co-ordinates of the point P will be (-3, -2) (b)

Question 4.
The reflection of the point P (1, – 2) in the line y = – 1 is
(a) ( – 3, – 2)
(b) (1, – 4)
(c) (1 , 4)
(d) (1, 0)
Solution:
The reflection of the point P (1, -2) in the line y = -1 is (1, 0) (d)

Question 5.
The reflection of the point A (4, -1) in the line x = 2 is
(a) (0, – 1)
(b) (8, – 1)
(c) (0, 1)
(d) none of these
Solution:
The reflection of A (4, -1) in the line x = 2 will be A’ (0, -1) (a)

Question 6.
The reflection of the point ( – 3, 0) in the origin is the point
(a) (0, – 3)
(b) (0, 3)
(c) (3, 0)
(d) none of these
Solution:
Reflection of the point (-3, 0) in origin will be (3, 0) (c)

Question 7.
Which of the following points is invariant with respect to the line y = – 2 ?
(a) (3, 2)
(b) (3, – 2)
(c) (2, 3)
(d) ( – 2, 3)
Solution:
The variant points are (3, -2) (b)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Can 0 be a term of a geometric progression?
Solution:
No, 0 is not a term of geometric progression.

Question 2.
(i) Find the next term of the list of numbers \(\frac { 1 }{ 6 } ,\frac { 1 }{ 3 } ,\frac { 2 }{ 3 } ,… \)
(ii) Find the next term of the list of numbers \(\frac { 3 }{ 16 } ,-\frac { 3 }{ 8 } ,\frac { 3 }{ 4 } ,-\frac { 3 }{ 2 } ,…\)
(iii) Find the 15th term of the series \(\sqrt { 3 } +\frac { 1 }{ \sqrt { 3 } } +\frac { 1 }{ 3\sqrt { 3 } } +…\)
(iv) Find the nth term of the list of numbers \(\frac { 1 }{ \sqrt { 2 } } ,-2,4\sqrt { 2 } ,-16,…\)
(v) Find the 10th and nth terms of the list of numbers 5, 25, 125, …
(vi) Find the 6th and the nth terms of the list of numbers \(\frac { 3 }{ 2 } ,\frac { 3 }{ 4 } ,\frac { 3 }{ 8 } ,…\)
(vii) Find the 6th term from the end of the list of numbers 3, – 6, 12, – 24, …, 12288.
Solution:
(i) Given
⇒ \(\frac { 1 }{ 6 } ,\frac { 1 }{ 3 } ,\frac { 2 }{ 3 } ,… \)

Question 3.
Which term of the G.P.
(i) 2, 2√2, 4, … is 128?
(ii) \(1,\frac { 1 }{ 3 } ,\frac { 1 }{ 9 } ,…is\quad \frac { 1 }{ 243 } ?\)
(iii) \(\frac { 1 }{ 3 } ,\frac { 1 }{ 9 } ,\frac { 1 }{ 27 } ,…is\quad \frac { 1 }{ 19683 } ? \)
Solution:
Given
(i) 2, 2√2, 4, … is 128?
Here a = 2, \(r=\frac { 2\sqrt { 2 } }{ 2 } =\sqrt { 2 } \), l = 128

Question 4.
Which term of the G.P. 3, – 3√3, 9, – 9√3, … is 729 ?
Solution:
G.P. 3, -3√3, 9, – 9√3, … is 729 ?
Here a = 3, \(r=\frac { -3\sqrt { 3 } }{ 3 } =\sqrt { -3 } \), l = 729

Question 5.
Determine the 12th term of a G.P. whose 8th term is 192 and common ratio is 2.
Solution:
In a G.P.
a₈ = 192 and r = 2
Let a be the first term and r be the common ratio then.

∴ a₁₂ = 3072

Question 6.
In a GP., the third term is 24 and 6th term is 192. Find the 10th term
Solution:
In a GP.
a₃ = 24 and a₆ = 192, a₁₀ = ?
Let a be the first term and r be the common ratio, therefore

Question 7.
Find the number of terms of a G.P. whose first term is \(\\ \frac { 3 }{ 4 } \), common ratio is 2 and the last term is 384.
Solution:
First term of a G.P. (a) = \(\\ \frac { 3 }{ 4 } \)
and common ratio (r) = 2
Last term = 384
Let number of terms is n

Question 8.
Find the value of x such that
(i) \(-\frac { 2 }{ 7 } ,x,-\frac { 7 }{ 2 } \) are three consecutive terms of a G.P.
(ii) x + 9, x – 6 and 4 are three consecutive terms of a G.P.
(iii) x, x + 3, x + 9 are first three terms of a G.P. Sol. Find the value of x
Solution:
Find the value of x
(i) \(-\frac { 2 }{ 7 } ,x,-\frac { 7 }{ 2 } \) are three consecutive terms of a G.P.

Question 9.
If the fourth, seventh and tenth terms of a G.P. are x, y, z respectively, prove that x, y, z are in G.P.
Solution:
In a G.P.
a₄ = x, a₇ = y, a₁₀ = z
To prove : x, y, z are in G.P.
Let a be the first term and r be the common

Question 10.
The 5th, 8th and 11th terms of a G.P. are p, q and s respectively. Show that q² = ps.
Solution:
In a G.P.
a₅ = p, a₈ = q and a₁₁ = s
To show that q² = px
Let a be the first term and r be the common

Question 11.
If a, b, c are in G.P., then show that a², b², c² are also in G.P.
Solution:
a, b, c are in G.P.
Show that a², b², c² are also in G.P
∵ a, b, c are in G.P., then
b² = ac …(i)
a², b², c² will be in G.P.
if (b²)² = a² x c²
⇒ (ac)² = a²c² [From (i)]
⇒ a²c² = a²c² which is true.
Hence proved.

Question 12.
If a, b, c are in A.P., then show that 3^a, 3^b, 3^c are in G.P.
Solution:
a, b and c are in A.P.
Then, 2b = a + c
Now, 3^a, 3^b, 3^c will be in G.P.
if (3^b)² = 3^a.3^c
if 3^2b = 3^a+c
Comparing, we get
if 2b = a + c
Which are in A.P. is given

Question 13.
If a, b, c are in A.P., then show that 10^{ax + 10}, 10^{bx + 10}, 10^{cx + 10}, x ≠ 0, are in G.P.
Solution:
a, b, c are in A.P.
To show that are in G.P.10^{ax + 10}, 10^{bx + 10}, 10^{cx + 10}, x ≠ 0
∵ a, b, c are in A.P.

Question 14.
If a, a²+ 2 and a³ + 10 are in G.P., then find the values(s) of a.
Solution:
a, a² + 2 and a³ + 10 are in G.P.
∵ (a² + 2)² = a(a³ + 10)

Question 15.
If k, 2k + 2, 3k + 3, … are in G.P., then find the common ratio of the G.P.
Solution:
k, 2k + 2, 3k + 3, … are in G.P.
then, (2k + 2)² = k(3k + 3)
⇒ 4k² + 8k + 4 = 3k² + 3k
⇒ 4k² + 8k + 4 – 3k² – 3k = 0

Question 16.
The first and the second terms of a GP. are x^-4 and x^m . If its 8th term is x⁵², then find the value of m.
Solution:
In a G.P.,
First term (a₁) = x^-4 …(i)
Second term (a₂) = x^m
Eighth term (a₈) = x⁵²

Question 17.
Find the geometric progression whose 4th term is 54 and the 7th Term is 1458.
Solution:
In a G.P.,
4th term (a₄) = 54

Question 18.
The fourth term of a GP. is the square of its second term and the first term is – 3. Determine its seventh term.
Solution:
In a GP.
a_n is square of a₂ i.e. an = (a₂)²
a₁ = – 3

Question 19.
The sum of first three terms of a G.P. is \(\\ \frac { 39 }{ 10 } \) and their product is 1. Find the common ratio and the terms.
Solution:
Sum of first three terms of G.P. = \(\\ \frac { 39 }{ 10 } \)
and their product = 1

Question 20.
Three numbers are in A.P. and their sum is 15. If 1, 4 and 19 are added to these numbers respectively, the resulting numbers are in G.P. Find the numbers.
Solution:
Given: Three numbers are in A.P. and their sum = 15
Let a – d, a, a + d be the three number in A.P.

Question 21.
Three numbers form an increasing G.P. If the middle term is doubled, then the new numbers are in A.P. Find the common ratio of the G.P.
Solution:
Three numbers form an increasing G.P.
Let \(\\ \frac { a }{ r } \) ,a,ar be three numbers in G.P.
Double the middle term, we get

Question 22.
Three numbers whose sum is 70 are in GP. If each of the extremes is multiplied by 4 and the mean by 5, the numbers will be in A.P. Find the numbers.
Solution:
Three numbers are in G.P.
Let numbers be
\(\\ \frac { r }{ a } \), a, ar

Question 23.
There are four numbers such that first three of them form an A.P. and the last three form a GP. The sum of the first and third number is 2 and that of second and fourth is 26. What are these numbers?
Solution:
There are 4 numbers, such that
First 3 numbers are in A.P. and
last 3 numbers are in GP.
Sum of first and third numbers = 2
and sum of 2nd and 4th = 26

Question 24.
(i) If a, b, c are in A.P. as well in G.P., prove that a = b = c.
(ii) If a, b, c are in A.P as well as in G.P., then find the value of a^b-c + b^c-a + c^a-b
Solution:
(i) a, b, c are in A.P. as well as in GP.
To prove: a = b = c
a, b, c are in A.P.

Question 25.
The terms of a G.P. with first term a and common ratio r are squared. Prove that resulting numbers form a G.P. Find its first term, common ratio and the nth term.
Solution:
In a G.P.,
The first term = a
and common ratio = r
GP. is a, ar, ar²
Squaring we get

Question 26.
Show that the products of the corresponding terms of two G.P.’s a, ar, ar², …, ar^n-1 and A, AR, AR², …, AR^n-1 form a G.P. and find the common ratio.
Solution:
It has to be proved that the sequence
aA, arAR, ar²AR², …, ar^n-1AR^n-1 and forms a G.P.

Question 27.
(i) If a, b, c are in G.P. show that \(\frac { 1 }{ a } ,\frac { 1 }{ b } ,\frac { 1 }{ c } \) are also in G.P.
(ii) If K is any positive real number and K^a, K^b K^c are three consecutive terms of a G.P., prove that a, b, c are three consecutive terms of an A.P.
(iii) If p, q, r are in A.P., show that pth, qth and rth terms of any G.P. are themselves in GP.
Solution:
(i) a, b, c are in G.P.
∴ b² = ac
\(\frac { 1 }{ a } ,\frac { 1 }{ b } ,\frac { 1 }{ c } \) will be in G.P.

Question 28.
If a, b, c are in GP., prove that the following are also in G.P.
(i) a³, b³, c³
(ii) a² + b², ab + bc, b² + c².
Solution:
(i) a, b, c are in G.P.
∴ b² = ac
a³, b³, c³ are in G.P.

Question 29.
If a, b, c, d are in G.P., show that
(i) a² + b², b² + c², c² + d² are in G.P.
(ii) (b – c)² + (c – a)² + (d – b)² = (a – d)².
Solution:
a, b, c, d are in G.P.
Let r be the common ratio, then a = a
b = ar, c = ar², d = ar³

Question 30.
The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour?
Solution:
Bacteria in the beginning = 30 = a
After every hours, it doubles itself
After 1 hour it becomes = 30 x 2 = 60 = ar
After 2 hours it will becomes = 60 x 2 = 120 = a²
After 3 hours, it will becomes = 120 x 2 = 240 = a³
After 4 hours it will becomes = 240 x 2 = 480 = a⁴
∴ After n hour, it will become = arⁿ

Question 31.
The length of the sides of a triangle form a G.P. If the perimeter of the triangle is 37 cm and the shortest side is of length 9 cm, find the lengths of the other two sides.
Solution:
Lengths of a triangle are in GP. and its sum is 37 cm
Let sides be a, ar, ar²
a + ar + ar² = 37
a = 9

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

Question 1.
Find the co-ordinates of the images of the following points under reflection in the x- axis:
(i) (2, -5)
(ii) \(-\frac { 3 }{ 2 } ,-\frac { 1 }{ 2 } \)
(iii) ( – 7, 0)
Solution:
Co-ordinates of the images of the points
under reflection in the x-axis will be
(i) Image of (2, -5) will be (2, 5)
(ii) Image of \(-\frac { 3 }{ 2 } ,-\frac { 1 }{ 2 } \) will be \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of ( -7, 0) will be (-7, 0)

Question 2.
Find the co-ordinates of the images of the following points under reflection in the y-axis:
(i) (2, – 5)
(ii) \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) (0, – 7)
Solution:
Co-ordinates of the image of the points under reflection in the y-axis
(i) Image of (2, -5) will be ( -2, -5)
(ii) Image of \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \) will be \(\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of (0, -7) will be (0, -7)

Question 3.
Find the co-ordinates of the images of the following points under reflection in the origin:
(i) (2, – 5)
(ii) \(\frac { -3 }{ 2 } ,\frac { -1 }{ 2 } \)
(iii) (0, 0)
Solution:
Co-ordinates of the image of the points under reflection in the y-axis
(i) Image of (2, -5) will be (-2, 5)
(ii) Image of \(\frac { -3 }{ 2 } ,\frac { -1 }{ 2 } \) will be \(\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of (0, 0) will be (0, 0)

Question 4.
The image of a point P under reflection in the x-axis is (5, – 2). Write down the co-ordinates of P.
Solution:
As the image of a point (5, -2) under x – axis is P
∴ Co-ordinates of P will be (5, 2)

Question 5.
A point P is reflected in the x-axis. Co-ordinates of its image are (8, – 6).
(i) Find the co-ordinates of P.
(ii) Find the co-ordinates of the image of P under reflection in the y-axis.
Solution:
The co-ordinates of image of P which is reflected in x-axis are (8, – 6), then
(0 Co-ordinates of P will be (8, 6)
(ii) Co-ordinates of image of P under reflection in the y-axis will be ( – 8, 6)

Question 6.
A point P is reflected in the origin. Co-ordinates of its image are (2, – 5). Find
(i) the co-ordinates of P.
(ii) the co-ordinates of the image of P in the x-axis.
Solution:
The co-ordinates of image of a point P which is reflected in origin are (2, – 5), then
(i) Co-ordinates of P will be ( – 2, 5)
(ii) Co-ordinates of the image of P in the x- axis will be ( – 2, – 5)

Question 7.
(i) The point P (2, 3) is reflected in the line x = 4 to the point P’. Find the co-ordinates of the point P’.
(ii) Find the image of the point P (1, – 2) in the line x = – 1.
Solution:
(i) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit
(b) Plot point P (2, 3) on it.
(c) Draw a line x = 4 which is parallel to y-axis.
(d) From P, draw a perpendicular on x = 4, which intersects x = 4 at Q.
(e) Produce PQ to P’, such that QP’ = QP.
∴ P’ is the reflection of P in the line x = 4
Co-ordinates of P’ are (6, 3)

(ii) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot the point P (1, -2) on it.
(c) Draw a line x = -1 which is parallel toy-axis.
(d) From P, draw a perpendicular on the line x = -1, which meets it at Q.
(e) Produce PQ to P’ such that PQ = QP’
P’ is the image or reflection of P in the line x = -1
Co-ordinates of P’ are (-3, -2)
Co-ordinates of P’ are (-3, -2)

Question 8.
(i) The point P (2, 4) on reflection in the line y = 1 is mapped onto P’ Find the co-ordinates of P’.
(ii) Find the image of the point P ( – 3, – 5) in the line y = – 2.
Solution:
(i) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot point P (2, 4) on it.
(c) Draw a line y = 1, which is parallel to x-axis.
(d) From P, draw a perpendicular on y = 1 meeting it at Q.
(e) Produce PQ to P’ such that QP’ = PQ.
P’ is the reflection of P whose co-ordinates are (2, -2)

(ii) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot point P (-3, -5) on it.
(c) Draw a line y = -2 which is parallel to the x-axis.
(d) From P, draw a perpendicular on y = -2 which meets it at Q.
(e) Produce PQ to P’ such that QP’ = PQ.
Then P’ is the image of P, whose co-ordinates are (-3, 1).

Question 9.
The point P ( – 4, – 5) on reflection in y-axis is mapped on P’. The point P’ on reflection in the origin is mapped on P”. Find the co-ordinates of P’ and P”. Write down a single transformation that maps P onto P”.
Solution:
P’ is the image of point P (-4, -5) in y-axis
∴Co-ordinates of P’ will be (4, -5)
Again P” is the image of P’ under reflection in origin will be (-4, 5).
The single transformation that maps P onto P” is the x-axis

Question 10.
Write down the co-ordinates of the image of the point (3, – 2) when :
(i) reflected in the x-axis
(ii) reflected in the y-axis
(iii) reflected in the x-axis followed by reflection in the y-axis
(iv) reflected in the origin. (2000)
Solution:
Co-ordinates of the given points are (3, -2).
(i) Co-ordinates of the image reflected in x- axis will be (3, 2)
(ii) Co-ordinates of the image reflected in y- axis will be (-3, -2)
(iii) Co-ordinates of the point reflected in x- axis followed by reflection in the y-axis will be (-3, 2)
(iv) Co-ordinates of the point reflected in the origin will be (-3, 2)

Question 11.
Find the co-ordinates of the image of (3, 1) under reflection in x-axis followed by a reflection in the line x = 1.
Solution:
(i) Draw axis XOX’ and YOY’ taking 1 cm = 1 unit.
(ii) Plot a point P (3, 1).
(iii) Draw a line x = 1, which is parallel to y-axis.
(iv) From P, draw a perpendicular on x-axis meeting it at Q.
(v) Produce PQ to P’ such that QP’ = PQ, then
P’ is the image of P is x-axis. Then co-ordinates of P’ will be (3, -1)
(vi) From P’, draw a perpendicular on x = 1 meeting it at R.
(vii) Produce P’R to P” such that RP” = P’R
∴P” is the image of P’ in the line x = 1
Co-ordinates of P” are (-1, -1)

Question 12.
If P’ ( – 4, – 3) is the image of a point P under reflection in the origin, find
(i) the co-ordinates of P.
(ii) the co-ordinates of the image of P under reflection in the line y = – 2.
Solution:
(i) Reflection of P is P’ (-4, -3) in the origin
∴ Co-ordinates of P will be (4, 3)
Draw a line y = -2, which is parallel to x-axis
(ii) From P, draw a perpendicular on y = -2 meetings it at Q
Produce PQ to P” such that QP” = PQ
∴P” will the image of P in the line y = -2
∴Co-ordinates of P” will be (4, -7)

Question 13.
A Point P (a, b) is reflected in the x-axis to P’ (2, – 3), write down the values of a and b. P” is the image of P, when reflected in the y-axis. Write down the co-ordinates of P”. Find the co-ordinates of P”’, when P is reflected in the line parallel to y-axis such that x = 4. (1998)
Solution:
P’ (2, -3) is the reflection of P (a, b) in the x-axis
∴Co-ordinates of P’ will be P’ (a, – b) but P’ is (2, -3)
Comparing a = 2, b = 3

∴Co-ordinates of P will be (2, 3)
P” is the image of P when reflected in y-axis
∴Co-ordinate of P” will be ( – 2, 3)
Draw a line x = 4, which is parallel to y-axis
and P'” is the image of P when it is reflected in the line x = 4,
then P'” is its reflection Co-ordinates of P”‘ will be (6, 3).

Question 14.
(i) Point P (a, b) is reflected in the x-axis to P’ (5, – 2). Write down the values of a and b.
(ii) P” is the image of P when reflected in the y-axis. Write down the co-ordinates of P”.
(iii) Name a single transformation that maps P’ to P”. (1997)
Solution:
(i) Image of P (a, b) reflected in the x-axis to P’ (5, -2)
∴ a = 5 and b = 2
(ii) P” is the image of P when reflected in the y-axis
∴ its co-ordinates will be (-5, -2).
(iii) The single transformation that maps P’ to P” is the origin.

Question 15.
Points A and B have co-ordinates (2, 5) and (0, 3). Find
(i) the image A’ of A under reflection in the x-axis.
(ii) the image B’ of B under reflection in the line AA’.
Solution:
Co-ordinates of A are (2, 5) and of B are (0, 3)

(i) Co-ordinates of A’, the image of A reflected in the x-axis will be (2, -5)
(ii) Co-ordinates of B’, the image of B under reflection in the line AA’ will be (4, 3).

Question 16.
Plot the points A (2, – 3), B ( – 1, 2) and C (0, – 2) on the graph paper. Draw the triangle formed by reflecting these points in the x-axis. Are the two triangles congruent?

Solution:
The points A (2, -3), B (-1, 2) and C(0, -2) has been plotted on the graph paper as shown and are joined to form a triangle ABC. The co-ordinates of the images of A, B and C reflected in x-axis will be A’ (2, 3), B’ (-1, -2), C’ (0, 2) respectively and are joined to from another ∆ A’B’C’
Yes, these two triangles are congruent.

Question 17.
The points (6, 2), (3, – 1) and ( – 2, 4) are the vertices of a right angled triangle. Check whether it remains a right angled triangle after reflection in the y-axis.
Solution:
Let A (6, 2), B (3, -1) and C (-2, 4) be the points of a right-angled triangle
then the co-ordinates of the images of A, B, C reflected in y-axis be
A’ (-6, 2), B’ (-3, -1) and C’ (2, 4).

By joining these points, we find that ∆A’B’C’ is also a right angled triangle.

Question 18.
The triangle ABC where A (1, 2), B (4, 8), C (6, 8) is reflected in the x-axis to triangle A’ B’ C’. The triangle A’ B’ C’ is then reflected in.the origin to triangle A”B”C” Write down the co-ordinates of A”, B”, C”. Write down a single transformation that maps ABC onto A” B” C”.
Solution:
The co-ordinates of ∆ ABC are A (1, 2) B (4, 8), C (6, 8)
which are reflected in x- axis as A’, B’ and C’.
∴ The co-ordinates of A’ (1, -2), B (4, -8) and C (6, -8).
A’, B’ and C’ are again reflected in origins to form an ∆A”B”C”.
∴ The co-ordinates of A” will be (-1, 2), B” (-4, 8) and C” (-6, 8)
The single transformation that maps ABC onto A” B” C” is y-axis.

Question 19.
The image of a point P on reflection in a line l is point P’. Describe the location of the line l.
Solution:
The line will be the right bisector of the line segment joining P and P’.

Question 20.
Given two points P and Q, and that (1) the image of P on reflection in y-axis is the point Q and (2) the mid point of PQ is invariant on reflection in x-axis. Locate
(i) the x-axis
(ii) the y-axis and
(iii) the origin.
Solution:
Q is the image of P on reflection in y-axis
and mid point of PQ is invariant on reflection in x-axis

(i) x-axis will be the line joining the points P and Q.
(ii) The line perpendicular bisector of line segment PQ is the y-axis.
(iii) The origin will be the mid point of line segment PQ.

Question 21.
The point ( – 3, 0) on reflection in a line is mapped as (3, 0) and the point (2, – 3) on reflection in the same line is mapped as ( – 2, – 3).
(i) Name the mirror line.
(ii) Write the co-ordinates of the image of ( – 3, – 4) in the mirror line.
Solution:
The point (-3,0) is the image of point (3, 0)
and point (2, -3) is image of point (-2, -3) reflected on the same line.
(i) It is clear that the mirror line will be y-axis.
(ii) The co-ordinates of the image of the point (-3, -4)
reflected in the same line i.e. y-axis will be (3, -4).

Question 22.
A ( – 2, 4) and B ( – 4, 2) are reflected in the y-axis. If A’ and B’ are images of A and B respectively, find

(i) the co-ordinates of A’ and B’.
(ii) Assign special name to quad. AA’B’B.
(iii) State whether AB’ = BA’.
Solution:
A (-2, 4) and B (-4, 2) are reflected in y- axis as A’ and B’.

(i) Co-ordinates of A’ are (2, 4) and of B are (4, 2).
(ii) The quadrilateral AA’ B’ B is an isosceles trapezium.
(iii) yes, AB’ = BA’

Question 23.
Use graph paper for this question.
(i) The point P (2, – 4) is reflected about the line x = 0 to get the image Q. Find the co-ordinates of Q.
(ii) Point Q is reflected about the line y = 0 to get the image R. Find the co-ordinates of R.
(iii) Name the figure PQR.
(iv) Find the area of figure PQR. (2007)
Solution:
(i) Since the point Q is the reflection of the point P (2, -4) in the line x = 0,
the co-ordinates of Q are (2, 4).
(ii) Since R is the reflection of Q (2, 4) about the line y = 0,
the co-ordinates of R are ( – 2, 4).
(iii) Figure PQR is the right angled triangle PQR.

(iv) Area of ∆ PQR = \(\\ \frac { 1 }{ 2 } \) x QR x PQ
= \(\\ \frac { 1 }{ 2 } \) x 4 x 8
= 16 sq. units.

Question 24.
Use graph paper for this question. The point P (5, 3) was reflected in the origin to get the image P’.
(i) Write down the co-ordinates of P’.
(ii) If M is the foot of perpendicular from P to the x-axis, find the co-ordinates of M.
(iii) If N is the foot of the perpendicular from P’ to the x-axis, find the co-ordinates of N.
(iv) Name the figure PMP’N.
(v) Find the area of the figure PMP’N. (2001)
Solution:
P’ is the image of point P (5, 3) reflected in the origin.

(i) Co-ordinates of P’ will be (-5, -3).
(ii) M is the foot of the perpendicular from P to the x-axis.
Co-ordinates of M will be (5, 0)
(iii) N is the foot of the perpendicular from P’ to x-axis.
Co-ordinates of N will be (-5, 0).
(iv) By joining the points, the figure PMP’N is a parallelogram.
(v) Area of the parallelogram = 2 x area of ∆ MPN
= 2 x \(\\ \frac { 1 }{ 2 } \) x MN x PM = MN x PM
= 10 x 3 = 30 sq. units. Ans.

Question 25.
Using a graph paper, plot the points A (6, 4) and B (0, 4).
(i) Reflect A and B in the origin to get the images A’ and B’.
(ii) Write the co-ordinates of A’ and B’.
(iii) State the geometrical name for the figure ABA’B’.
(iv) Find its perimeter.
Solution:
(i) A (6, 4), B (0, 4)

Perimeter = Sum of all sides = 6 + 10 + 6 + 10 = 32 units

Question 26.
Use graph paper to answer this question
(i) Plot the points A (4, 6) and B (1, 2).
(ii) If A’ is the image of A when reflected in x-axis, write the co-ordinates of A’.
(iii) If B’ is the image of B when B is reflected in the line AA’, write the co-ordinates of B’.
(iv) Give the geometrical name for the figure ABA’B’. (2009)
Solution:
(i) Plotting the points A (4, 6) and B (1, 2) on the given graph.
(ii) A’ = (4, -6)
(iii) B’ = (7, 2)
(iv) In the quadrilateral ABA’B’, we have AB = AB’ and A’B = A’B’
Hence, ABA’B’ is a kite.

Question 27.
The points A (2, 3), B (4, 5) and C (7, 2) are the vertices’s of ∆ABC. (2006)
(i) Write down the co-ordinates of A1, B1, C1 if ∆ A1B1C1 is the image of ∆ ABC when reflected in the origin.
(ii) Write down the co-ordinates of A2, B2, C2 if ∆ A2B2C2 is the image of ∆ ABC when reflected in the x-axis.
(iii) Assign the special name to the quadrilateral BCC2B2 and find its area.


Solution:
Points A (2, 3), B (4, 5) and C (7, 2) are the vertices’s of ∆ ABC.
A1, B1 and C1 are the images of A, B and C reflected in the origin.
(i) Co-ordinates of A1 = (-2, -3) of B1 (-4, -5) and of C1 (-7, -2).
(ii) Co-ordinates of A2, B2 and C2 the images of A, B and C
when reflected in x-axis are A2 (2, – 3), B2 (4, – 5), C2 (7, – 2)
(iii) The quadrilateral formed by joining the points,
BCC2B2 is an isosceles trapezium and its area

Question 28.
The point P (3, 4) is reflected to P’ in the x-axis and O’ is the image of O (origin) in the line PP’. Find :
(i) the co-ordinates of P’ and O’,
(ii) the length of segments PP’ and OO’.
(iii) the perimeter of the quadrilateral POP’O’.
Solution:
P’ is the image of P (3, 4) reflected in x- axis
and O’ is the image of O the origin in the line P’P.
(i) Co-ordinates of P’ are (3, -4)
and co-ordinates of O’ reflected in PP’ are (6, 0)
(ii) Length of PP’ = 8 units and OO’ = 6 units
(iii) Perimeter of POP’O’ is

Question 29.
Use a graph paper for this question. (Take 10 small divisions = 1 unit on both axes). P and Q have co-ordinates (0, 5) and ( – 2, 4).
(i) P is invariant when reflected in an axis. Name the axis.
(ii) Find the image of Q on reflection in the axis found in (i).
(iii) (0, k) on reflection in the origin is invariant. Write the value of k.
(iv) Write the co-ordinates of the image of Q, obtained by reflecting it in the origin followed by reflection in x-axis. (2005)
Solution:

(i) Two points P (0, 5) and Q (-2, 4) are given As the abscissa of P is 0.
It is invariant when is reflected in y-axis.
(ii) Let Q’ be the image of Q on reflection in y-axis.
Co-ordinate of Q’ will be (2, 4)
(iii) (0, k) on reflection in the origin is invariant.
co-ordinates of image will be (0, 0). k = 0
(iv) The reflection of Q in the origin is the point Q”
and its co-ordinates will be (2, – 4)
and reflection of Q” (2, – 4) in x-axis is (2, 4) which is the point Q’

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test

Question 1.
Check whether the following are quadratic equations:
(i)\(\sqrt { 3 } { x }^{ 2 }-2x+\frac { 3 }{ 5 } =0\)
(ii)(2x + 1) (3x – 2) = 6(x + 1) (x – 2)
(iii)\({ (x-3) }^{ 3 }+5={ x }^{ 3 }+7{ x }^{ 2 }-1\)
(iv)\(x-\frac { 3 }{ x } =2,x\neq 0\)
(v)\(x+\frac { 2 }{ x } ={ x }^{ 2 },x\neq 0\)
(vi)\({ x }^{ 2 }+\frac { 1 }{ { x }^{ 2 } } =3,x\neq 0 \)
Solution:
(i) \(\sqrt { 3 } { x }^{ 2 }-2x+\frac { 3 }{ 5 } =0\)
It is a quadratic equation as it is power of 2.
(ii) (2x + 1) (3x – 2) = 6(x + 1) (x – 2)
6x² – 4x + 3x – 2 = 6(x² – 2x + x – 2)
6x² – x – 2 = 6x² – 12x + 6x – 12

Question 2.
In each of the following, determine whether the given numbers are roots of the given equations or not;
(i) x² – x + 1 = 0; 1, – 1
(ii) x² – 5x + 6 = 0; 2, – 3
(iii) 3x² – 13x – 10 = 0; 5,\(\\ \frac { -2 }{ 3 } \)
(iv) 6x² – x – 2 = 0;\(\\ \frac { -1 }{ 2 } \), \(\\ \frac { 2 }{ 3 } \)
Solution:
(i) x² – x + 1 = 0; 1, -1
Where x = 1, then
(1)² – 1 + 1 = 1 – 1 + 1 = 1 ≠ 0
∴ x = 1 does not satisfy it

Question 3.
In each of the following, determine whether the given numbers are solutions of the given equation or not:
(i) x² – 3√3x + 6 = 0; √3, – 2√3
(ii) x² – √2x – 4 = 0, x = – √2, 2√2
Solution:
(i) x² – 3√3x + 6 = 0; √3, -2√3
(a) Substituting the value of x = √3

Question 4.
(i) If \(– \frac { 1 }{ 2 } \) is a solution of the equation 3x² + 2kx – 3 = 0, find the value of k.
(ii) If \(\\ \frac { 2 }{ 3 } \) is a solution of the equation 7x² + kx – 3 = 0, find the value of k.
Solution:
(i) x = \(– \frac { 1 }{ 2 } \) is a solution of the
3x² + 2kx – 3 = 0,
Substituting the value of x in the given equation

Question 5.
(i) If √2 is a root of the equation kx² + √2 – 4 = 0, find the value of k.
(ii) If a is a root of the equation x² – (a + b)x + k = 0, find the value of k.
Solution:
(i) kx² + √2 – 4 = 0, x = √2
x = √2 is its solution

Question 6.
If \(\\ \frac { 2 }{ 3 } \) and – 3 are the roots of the equation px² + 7x + q = 0, find the values of p and q.
Solution:
\(\\ \frac { 2 }{ 3 } \) and – 3 are the roots of the equation px² + 7x + q = 0
Substituting the value of x = \(\\ \frac { 2 }{ 3 } \) and – 3 respectively, we get

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test

Choose the correct answer from the given four options (1 to 15) :

Question 1.
Which of the following is not a quadratic equation ?
(a) (x + 2)² = 2(x + 3)
(b) x² + 3x = ( – 1) (1 – 3x)
(c) (x + 2) (x – 1) = x² – 2x – 3
(d) x³ – x² + 2x + 1 = (x + 1)³
Solution:
(a) (x + 2)² = 2(x + 3)
⇒ x² + 4x + 4 = 2x + 6
⇒ x² + 4x – 2x + 4 – 6 = 0
⇒ x² + 2x – 2
It is a quadratic equation.

Question 2.
Which of the following is a quadratic equation ?
(a) (x – 2) (x + 1) = (x – 1) (x – 3)
(b) (x + 2)³ = 2x(x² – 1)
(c) x² + 3x + 1 = (x – 2)²
(d) 8(x – 2)³ = (2x – 1)³ + 3
Solution:
(a) (x – 2) (x + 1) = (x – 1) (x – 3)
⇒ x² + x – 2x – 2 = x² – 3x – x + 3
⇒ 3x + x – 2x + x = 3 + 2
⇒ 3x = 5
It is not a quadratic equation.

Question 3.
Which of the following equations has 2 as a root ?
(a) x² – 4x + 5 = 0
(b) x² + 3x – 12 = 0
(c) 2x² – 7x + 6 = 0
(d) 3x² – 6x – 2 = 0
Solution:
(a) x² – 4x + 5 = 0
⇒ (2)² – 4x² + 5 = 0
⇒ 4 – 8 + 5 = 0
⇒ 9 – 8 ≠ 0
2 is not its root.

Question 4.
If \(\\ \frac { 1 }{ 2 } \) is a root of the equation x² + kx – \(\\ \frac { 5 }{ 4 } \) = 0, then the value of k is
(a) 2
(b) – 2
(c) \(\\ \frac { 1 }{ 4 } \)
(d) \(\\ \frac { 1 }{ 2 } \)
Solution:
\(\\ \frac { 1 }{ 2 } \) is a root of the equation
x² + kx – \(\\ \frac { 5 }{ 4 } \) = 0
Substituting the value of x = \(\\ \frac { 1 }{ 2 } \) in the

Question 5.
If \(\\ \frac { 1 }{ 2 } \) is a root of the quadratic equation 4x² – 4kx + k + 5 = 0, then the value of k is
(a) – 6
(b) – 3
(c) 3
(d) 6
Solution:
\(\\ \frac { 1 }{ 2 } \) is a root of the equation
4x² – 4kx + k + 5 = 0

Question 6.
The roots of the equation x² – 3x – 10 = 0 are
(a) 2,- 5
(b) – 2, 5
(c) 2, 5
(d) – 2, – 5
Solution:
x² – 3x – 10 = 0

x = 5, – 2 or – 2, 5 (b)

Question 7.
If one root of a quadratic equation with rational coefficients is \(\frac { 3-\sqrt { 5 } }{ 2 } \), then the other
(a)\(\frac { -3-\sqrt { 5 } }{ 2 } \)
(b)\(\frac { -3+\sqrt { 5 } }{ 2 } \)
(c)\(\frac { 3+\sqrt { 5 } }{ 2 } \)
(d)\(\frac { \sqrt { 3 } +5 }{ 2 } \)
Solution:
One root of a quadratic equation is \(\frac { 3-\sqrt { 5 } }{ 2 } \)
then other root will be \(\frac { 3+\sqrt { 5 } }{ 2 } \) (c)

Question 8.
If the equation 2x² – 5x + (k + 3) = 0 has equal roots then the value of k is
(a)\(\\ \frac { 9 }{ 8 } \)
(b)\(– \frac { 9 }{ 8 } \)
(c)\(\\ \frac { 1 }{ 8 } \)
(d)\(– \frac { 1 }{ 8 } \)
Solution:
2x² – 5x + (k + 3) = 0
a = 2, b = -5, c = k + 3

Question 9.
The value(s) of k for which the quadratic equation 2x² – kx + k = 0 has equal roots is (are)
(a) 0 only
(b) 4
(c) 8 only
(d) 0, 8
Solution:
2x² – kx + k = 0
a = 2, b = -k, c = k

Question 10.
If the equation 3x² – kx + 2k =0 roots, then the the value(s) of k is (are)
(a) 6
(b) 0 Only
(c) 24 only
(d) 0
Solution:
3x² – kx + 2k = 0
Here, a = 3, b = -k, c = 2k

Question 11.
If the equation {k + 1)x² – 2(k – 1)x + 1 = 0 has equal roots, then the values of k are
(a) 1, 3
(b) 0, 3
(c) 0, 1
(d) 0, 1
Solution:
(k + 1)x² – 2(k – 1)x + 1 = 0
Here, a = k + 1, b = -2(k – 1), c = 1

k = 0, 3 (b)

Question 12.
If the equation 2x² – 6x + p = 0 has real and different roots, then the values ofp are given by
(a)p < \(\\ \frac { 9 }{ 2 } \)
(b)p ≤ \(\\ \frac { 9 }{ 2 } \)
(c)p > \(\\ \frac { 9 }{ 2 } \)
(d)p ≥ \(\\ \frac { 9 }{ 2 } \)
Solution:
2x² – 6x + p = 0
Here, a = 2, b = -6, c = p

Question 13.
The quadratic equation 2x² – √5x + 1 = 0 has
(a) two distinct real roots
(b) two equal real roots
(c) no real roots
(d) more than two real roots
Solution:
2x² – √5x + 1 = 0
Here, a = 2, b = -√5, c = 1

Question 14.
Which of the following equations has two distinct real roots ?
(a) 2x² – 3√2x + \(\\ \frac { 9 }{ 4 } \) = 0
(b) x² + x – 5 = 0
(c) x² + 3x + 2√2 = 0
(d) 5x² – 3x + 1 = 0
Solution:
(a) 2x² – 3√2x + \(\\ \frac { 9 }{ 4 } \) = 0
b² – 4ac = ( -3√2)² – 4 x 2 x \(\\ \frac { 9 }{ 4 } \) = 18 – 18 = 0
.’. Roots are real and equal.

Question 15.
Which of the following equations has no real roots ?
(a) x² – 4x + 3√2 = 0
(b) x² + 4x – 3√2 = 0
(c) x² – 4x – 3√2 = 0
(d) 3x² + 4√3x + 4 = 0
Solution:
(a) x² – 4x + 3√2 = 0
b² – 4ac = ( -4)² – 4 × 1 × 3√2
= 16 – 12√2
= 16 – 12(1.4)
= 16 – 16.8
= -0.8
b² – 4ac < 0
Roots are not real. (a)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Chapter Test

Question 1.
Find the value of x in the following proportions :
(i) 10 : 35 = x : 42
(ii) 3 : x = 24 : 2
(iii) 2.5 : 1.5 = x : 3
(iv) x : 50 :: 3 : 2
Solution:
(i) 10 : 35 = x : 42
⇒ 35 × x = 10 × 42

Question 2.
Find the fourth proportional to
(i) 3, 12, 15
(ii) \(\frac { 1 }{ 3 } ,\frac { 1 }{ 4 } ,\frac { 1 }{ 5 } \)
(iii) 1.5, 2.5, 4.5
(iv) 9.6 kg, 7.2 kg, 28.8 kg
Solution:
(i) Let fourth proportional to
3, 12, 15 be x.
then 3 : 12 :: 15 : x

Question 3.
Find the third proportional to
(i) 5, 10
(ii) 0.24, 0.6
(iii) Rs. 3, Rs. 12
(iv) \(5 \frac { 1 }{ 4 } \) and 7.
Solution:
(i) Let x be the third proportional to 5, 10,
then 5 : 10 :: 10 : x

Question 4.
Find the mean proportion of:
(i) 5 and 80
(ii) \(\\ \frac { 1 }{ 12 } \) and \(\\ \frac { 1 }{ 75 } \)
(iii) 8.1 and 2.5
(iv) (a – b) and (a³ – a²b), a> b
Solution:
(i) Let x be the mean proportion of 5 and 80 ,
then 5 : x : : x : 80
x² = 5 x 80
⇒ x = \(\sqrt { 5\times 80 } =\sqrt { 400 } \) = 20
x = 20

Question 5.
If a, 12, 16 and b are in continued proportion find a and b.
Solution:
∵ a, 12, 16, b are in continued proportion, then

Question 6.
What number must be added to each of the numbers 5, 11, 19 and 37 so that they are in proportion ? (2009)
Solution:
Let x be added to 5, 11, 19 and 37 to make them in proportion.
5 + x : 11 + x : : 19 + x : 37 + x

Question 7.
What number should be subtracted from each of the numbers 23, 30, 57 and 78 so that the remainders are in proportion ? (2004)
Solution:
Let x be subtracted from each term, then
23 – x, 30 – x, 57 – x and 78 – x are proportional
23 – x : 30 – x : : 57 – x : 78 – x

Question 8.
If 2x – 1, 5x – 6, 6x + 2 and 15x – 9 are in proportion, find the value of x.
Solution:
∵ 2x – 1, 5x – 6, 6x + 2 and 15x – 9 are in proportion.
then (2x – 1) (15x – 9) = (5x – 6) (6x + 2)

Question 9.
If x + 5 is the mean proportion between x + 2 and x + 9, find the value of x.
Solution:
∵ x + 5 is the mean proportion between x + 2 and x + 9, then
(x + 5)² = (x + 2) (x + 9)
⇒ x² + 10x + 25 = x² + 11x + 18
⇒ x² + 10x – x² – 11x = 18 – 25
⇒ – x = – 7
∵ x = 7 Ans.

Question 10.
What number must be added to each of the numbers 16, 26 and 40 so that the resulting numbers may be in continued proportion?
Solution:
Let x be added to each number then
16 + x, 26 + x and 40 + x
are in continued proportion.

Question 11.
Find two numbers such that the mean proportional between them is 28 and the third proportional to them is 224.
Solution:
Let the two numbers are a and b.
∵ 28 is the mean proportional
∵ a : 28 : : 28 : b

Question 12.
If b is the mean proportional between a and c, prove that a, c, a² + b², and b² + c² are proportional.
Solution:
∵ b is the mean proportional between a and c, then,
b² = a × c ⇒ b² = ac …(i)

Question 13.
If b is the mean proportional between a and c, prove that (ab + bc) is the mean proportional between (a² + b²) and (b² + c²).
Solution:
b is the mean proportional between a and c then
b² = ac …(i)
Now if (ab + bc) is the mean proportional

Question 14.
If y is mean proportional between x and z, prove that
xyz (x + y + z)³ = (xy + yz + zx)³.
Solution:
∵ y is the mean proportional between
x and z, then
y² = xz …(i)

Question 15.
If a + c = mb and \(\frac { 1 }{ b } +\frac { 1 }{ d } =\frac { m }{ c } \), prove that a, b, c and d are in proportion.
Solution:
a + c = mb and \(\frac { 1 }{ b } +\frac { 1 }{ d } =\frac { m }{ c } \)
a + c = mb

Question 16.
If \(\frac { x }{ a } =\frac { y }{ b } =\frac { z }{ c } \), prove that
(i)\(\frac { { x }^{ 3 } }{ { a }^{ 2 } } +\frac { { y }^{ 3 } }{ { b }^{ 2 } } +\frac { { z }^{ 3 } }{ { c }^{ 2 } } =\frac { { \left( x+y+z \right) }^{ 3 } }{ { \left( a+b+c \right) }^{ 2 } } \)

Solution:
\(\frac { x }{ a } =\frac { y }{ b } =\frac { z }{ c } \)
∴ x = ak, y = bk, z = ck

Question 17.
If \(\frac { a }{ b } =\frac { c }{ d } =\frac { e }{ f } \) prove that :
(i) (b² + d² + f²) (a² + c² + e²) = (ab + cd + ef)²

Solution:
\(\frac { a }{ b } =\frac { c }{ d } =\frac { e }{ f } \) = k(say)
∴ a = bk, c = dk, e =fk

Question 18.
If ax = by = cz; prove that
\(\frac { { x }^{ 2 } }{ yz } +\frac { { y }^{ 2 } }{ zx } +\frac { { z }^{ 2 } }{ xy } \) = \(\frac { bc }{ { a }^{ 2 } } +\frac { ca }{ { b }^{ 2 } } +\frac { ab }{ { c }^{ 2 } } \)
Solution:
Let ax = by = cz = k

Question 19.
If a, b, c and d are in proportion, prove that:
(i) (5a + 7b) (2c – 3d) = (5c + 7d) (2a – 3b)
(ii) (ma + nb) : b = (mc + nd) : d
(iii) (a⁴ + c⁴) : (b⁴ + d⁴) = a² c² : b² d².

Solution:
∵ a, b, c, d are in proportion
\(\\ \frac { a }{ b } \) = \(\\ \frac { c }{ d } \) = k(say)

Question 20.
If x, y, z are in continued proportion, prove that:\(\frac { { \left( x+y \right) }^{ 2 } }{ { \left( y+z \right) }^{ 2 } } =\frac { x }{ z } \). (2010)
Solution:
x, y, z are in continued proportion
Let \(\\ \frac { x }{ y } \) = \(\\ \frac { y }{ z } \) = k

Question 21.
If a, b, c are in continued proportion, prove that:
\(\frac { { pa }^{ 2 }+qab+{ rb }^{ 2 } }{ { pb }^{ 2 }+qbc+{ rc }^{ 2 } } =\frac { a }{ c } \)
Solution:
Given a, b, c are in continued proportion
\(\frac { { pa }^{ 2 }+qab+{ rb }^{ 2 } }{ { pb }^{ 2 }+qbc+{ rc }^{ 2 } } =\frac { a }{ c } \)
Let \(\\ \frac { a }{ b } \) = \(\\ \frac { b }{ c } \) = k

Question 22.
If a, b, c are in continued proportion, prove that:
(i) \(\frac { a+b }{ b+c } =\frac { { a }^{ 2 }(b-c) }{ { b }^{ 2 }(a-b) } \)

Solution:
As a, b, c, are in continued proportion
Let \(\\ \frac { a }{ b } \) = \(\\ \frac { b }{ c } \) = k

Question 23.
If a, b, c, d are in continued proportion, prove that:
(i) \(\frac { { a }^{ 3 }+{ b }^{ 3 }+{ c }^{ 3 } }{ { b }^{ 3 }+{ c }^{ 3 }+{ d }^{ 3 } } =\frac { a }{ d } \)

Solution:
a, b, c, d are in continued proportion
∴ \(\frac { a }{ b } =\frac { b }{ c } =\frac { c }{ d } =k(say)\)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Question 1.
(i)\(\begin{bmatrix} 2 & -1 \\ 5 & 1 \end{bmatrix}\)
(ii)[2 3 – 7]
(iii)\(\left[ \begin{matrix} 3 \\ 0 \\ -1 \end{matrix} \right] \)
(iv)\(\left[ \begin{matrix} \begin{matrix} 2 \\ 0 \\ 1 \end{matrix} & \begin{matrix} -4 \\ 0 \\ 7 \end{matrix} \end{matrix} \right] \)
(v)\(\left[ \begin{matrix} \begin{matrix} 2 & 7 & 8 \end{matrix} \\ \begin{matrix} -1 & \sqrt { 2 } & 0 \end{matrix} \end{matrix} \right] \)
(vi)\(\left[ \begin{matrix} \begin{matrix} 0 & 0 & 0 \end{matrix} \\ \begin{matrix} 0 & 0 & 0 \end{matrix} \end{matrix} \right] \)
Solution:
(i) It is square matrix of order 2
(ii) It is row matrix of order 1 × 3
(iii) It is column matrix of order 3 × 1
(iv) It is matrix of order 3 × 2
(v) It is matrix of order 2 × 3
(vi) It is zero matrix of order 2 × 3

Question 2.
(i) If a matrix has 4 elements, what are the possible order it can have ?
(ii) If a matrix has 8 elements, what are the possible order it can have ?
Solution:
(i) It can have 1 × 4, 4 × 1 or 2 × 2 order
(ii) It can have 1 × 8, 8 × 1,2 × 4 or 4 × 2 order

Question 3.
Construct a 2 x 2 matrix whose elements a_ij are given by
(i) a_ij = 2i – j
(ii) a_ij = i.j
Solution:
(i) It can be \(\begin{bmatrix} 1 & 0 \\ 3 & 2 \end{bmatrix}\)
(ii) It can be \(\begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}\)

Question 4.
Find the values of x and y if : \(\left[ \begin{matrix} 2x+y \\ 3x-2y \end{matrix} \right] =\left[ \begin{matrix} 5 \\ 4 \end{matrix} \right] \)
Solution:
Comparing corresponding elements,
2x + y = 5 …(i)
3x – 2y = 4 …(ii)
Multiply (i) by 2 and (ii) by ‘1’ we get
4x + 2y = 10, 3x – 2y = 4
Adding we get, 7x = 14 ⇒ x = 2
Substituting the value of x in (i)
2 x 2 + y = 5 ⇒ 4 + y = 5
y = 5 – 4 = 1
Hence x = 2, y = 1

Question 5.
Find the value of x if \(\left[ \begin{matrix} \begin{matrix} 3x+y & \quad -y \end{matrix} \\ \begin{matrix} 2y-x & \quad \quad 3 \end{matrix} \end{matrix} \right] =\begin{bmatrix} 1 & 2 \\ -5 & 3 \end{bmatrix} \)
Solution:
\(\left[ \begin{matrix} \begin{matrix} 3x+y & \quad -y \end{matrix} \\ \begin{matrix} 2y-x & \quad \quad 3 \end{matrix} \end{matrix} \right] =\begin{bmatrix} 1 & 2 \\ -5 & 3 \end{bmatrix} \)
Comparing the corresponding terms, we get.
-y = 2
⇒ y = -2

Question 6.
If \(\left[ \begin{matrix} \begin{matrix} x+3 & \quad \quad 4 \end{matrix} \\ \begin{matrix} y-4 & \quad \quad x+y \end{matrix} \end{matrix} \right] =\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \) ,find values of x and y
Solution:
\(\left[ \begin{matrix} \begin{matrix} x+3 & \quad \quad 4 \end{matrix} \\ \begin{matrix} y-4 & \quad \quad x+y \end{matrix} \end{matrix} \right] =\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \)
Comparing the corresponding terms, we get.
x + 3 = 5
⇒ x = 5 – 3 = 2
⇒ y – 4 = 3
⇒ y = 3 + 4 = 7
x = 2, y = 7

Question 7.
Find the values of x, y and z if
\(\left[ \begin{matrix} \begin{matrix} x+2 & \quad \quad 6 \end{matrix} \\ \begin{matrix} 3 & \quad \quad \quad 5z \end{matrix} \end{matrix} \right] =\begin{bmatrix} -5 & \quad { y }^{ 2 }+y \\ 3 & -20 \end{bmatrix}\)
Solution:
Comparing the corresponding elements of equal determinents,
x + 2 = -5
⇒ x = -5 – 2 = -7

Question 8.
Find the values of x, y, a and b if
\(\begin{bmatrix} x-2 & y \\ a+2b & 3a-b \end{bmatrix}=\begin{bmatrix} 3 & 1 \\ 5 & 1 \end{bmatrix}\)
Solution:
Comparing corresponding elements
x – 2 = 3, y = 1
x = 3 + 2 = 5
a + 2b = 5 ……(i)
3a – b = 1 ……..(ii)

Question 9.
Find the values of a, b, c and d if
\(\begin{bmatrix} a+b & 3 \\ 5+c & ab \end{bmatrix}=\begin{bmatrix} 6 & d \\ -1 & 8 \end{bmatrix} \)
Solution:
\(\begin{bmatrix} a+b & 3 \\ 5+c & ab \end{bmatrix}=\begin{bmatrix} 6 & d \\ -1 & 8 \end{bmatrix} \)
Comparing the corresponding terms, we get.
3 = d ⇒ d = 3
⇒ 5 + c = – 1
⇒ c = -1 – 5
⇒ c = -6
a + b = 6 and ab = 8

Question 10.
Find the values of x, y, a and b, if
\(\left[ \begin{matrix} \begin{matrix} 3x+4y & 2 & x-2y \end{matrix} \\ \begin{matrix} a+b & 2a-b & -1 \end{matrix} \end{matrix} \right] =\left[ \begin{matrix} \begin{matrix} 2 & \quad 2\quad & 4 \end{matrix} \\ \begin{matrix} 5 & -5 & -1 \end{matrix} \end{matrix} \right] \)
Solution:
Comparing the corresponding terms, we get.
3x + 4y = 2 ……(i)
x – 2y = 4 …….(ii)
Multiplying (i) by 1 and (ii) by 2

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.