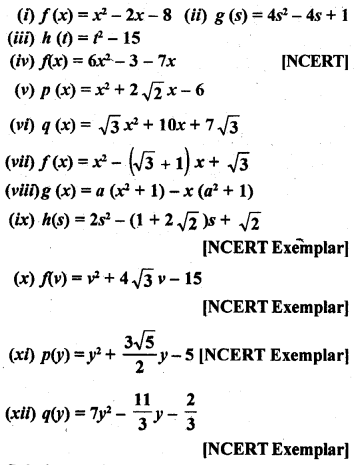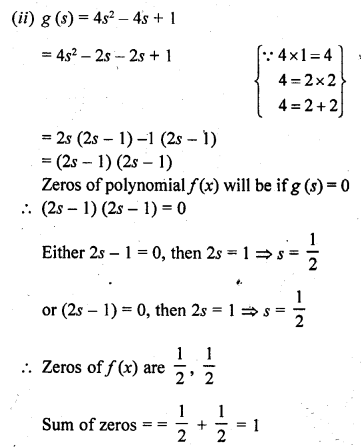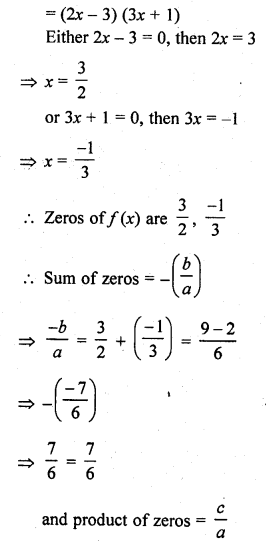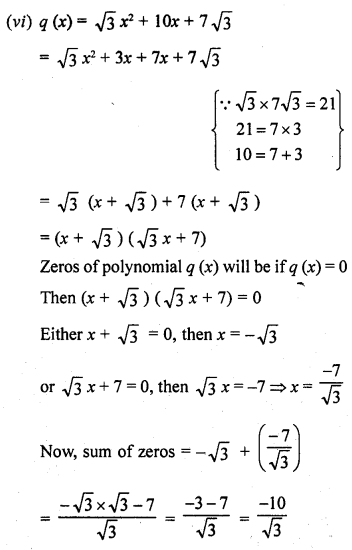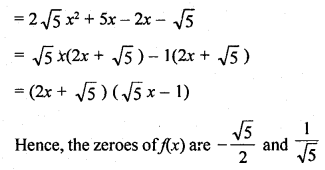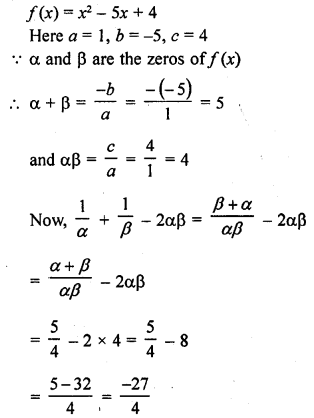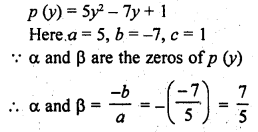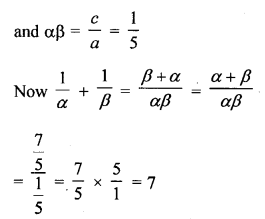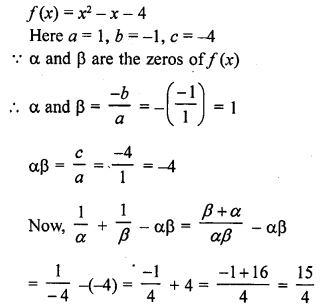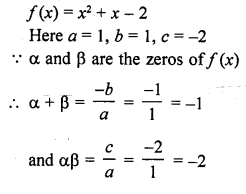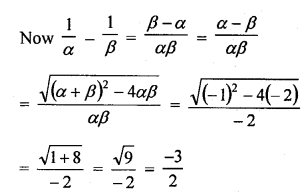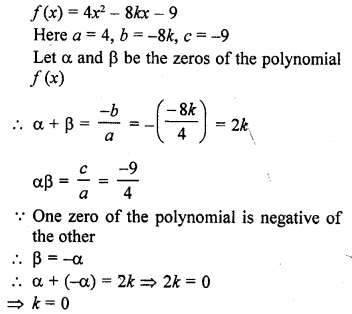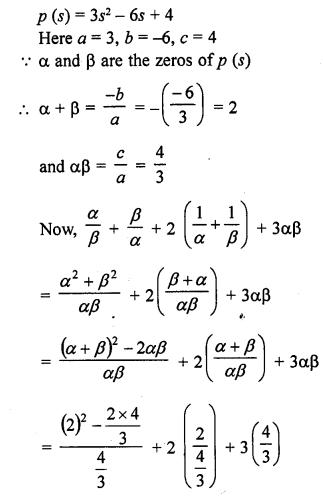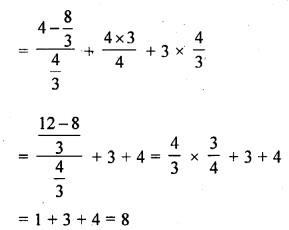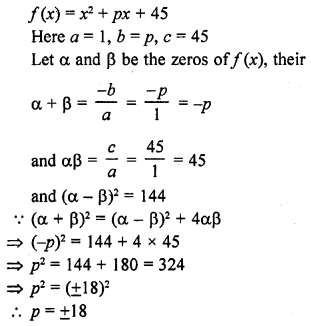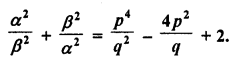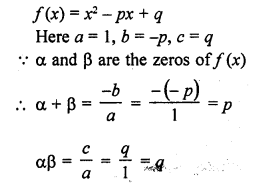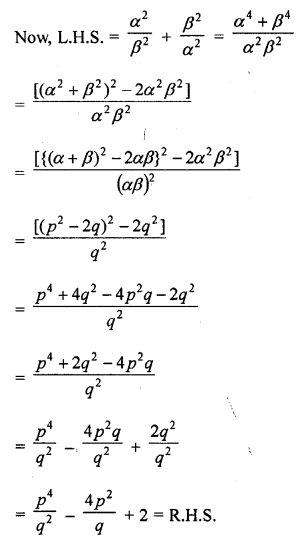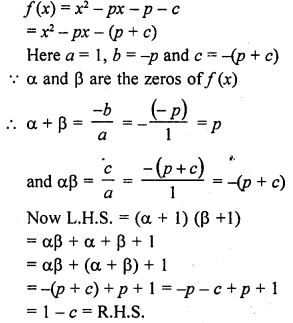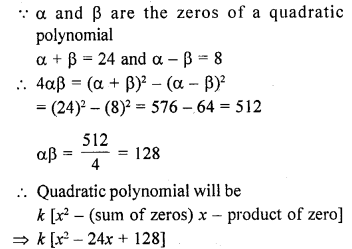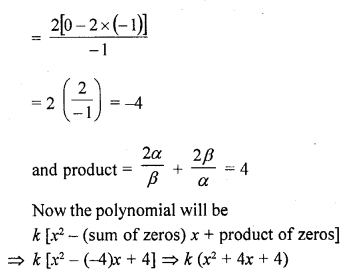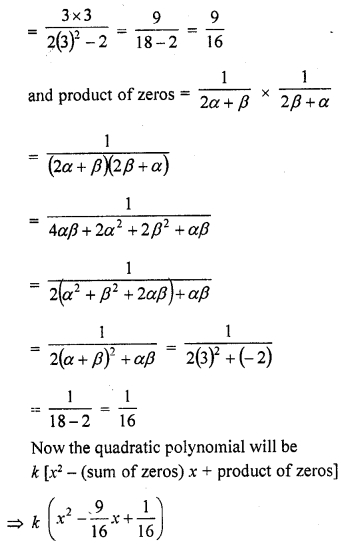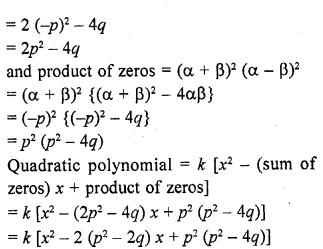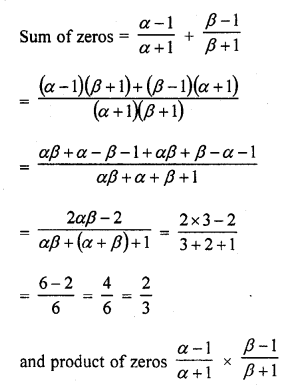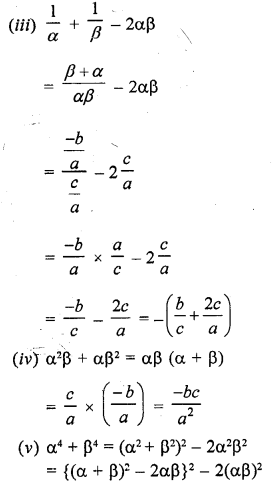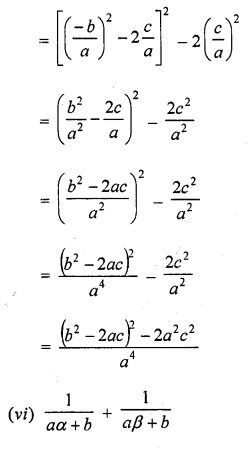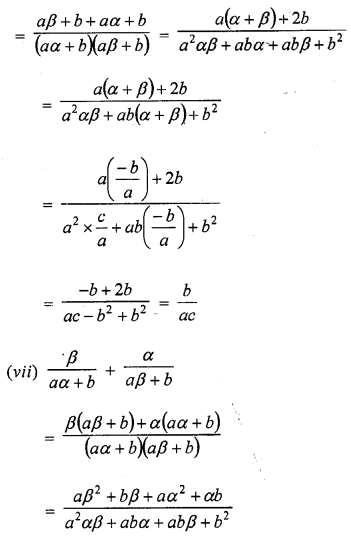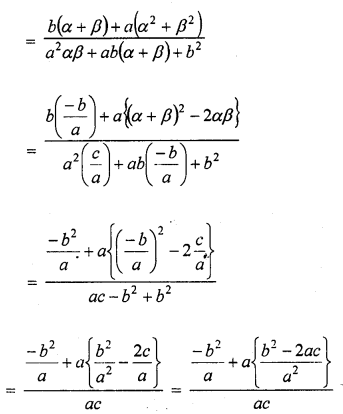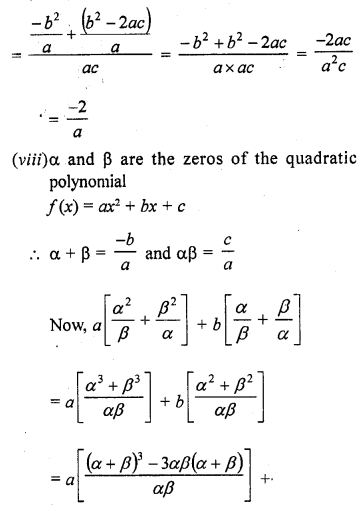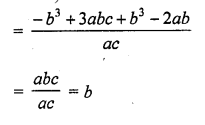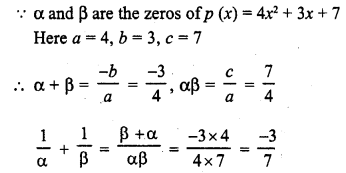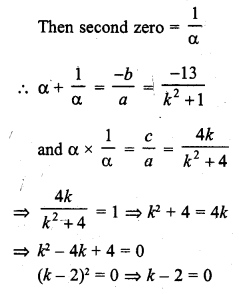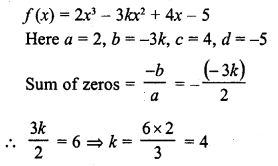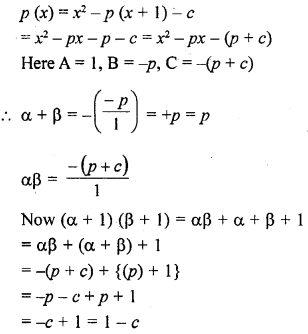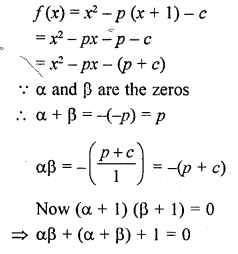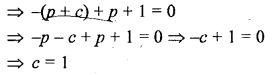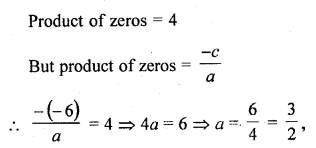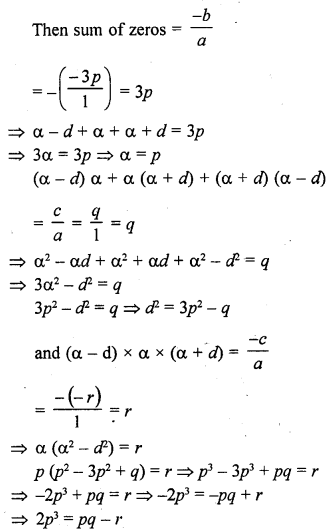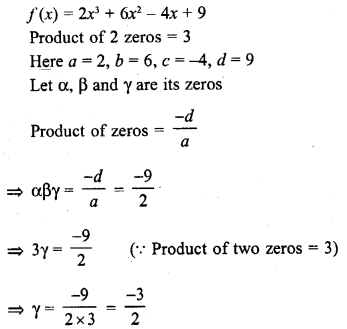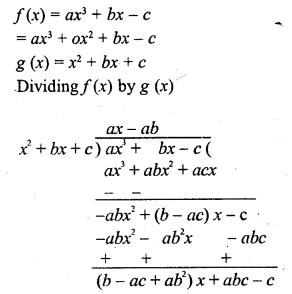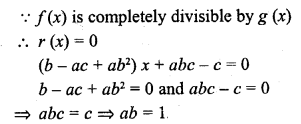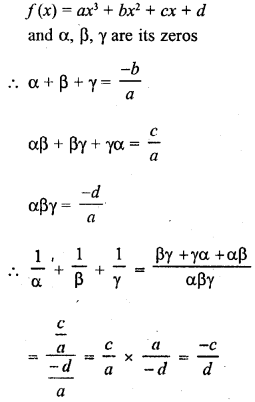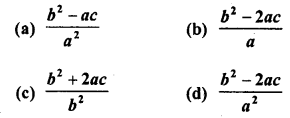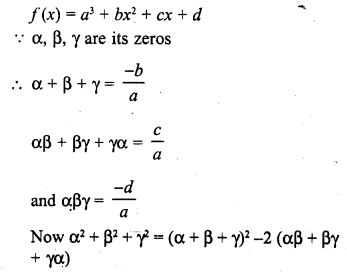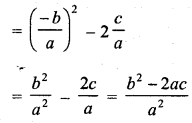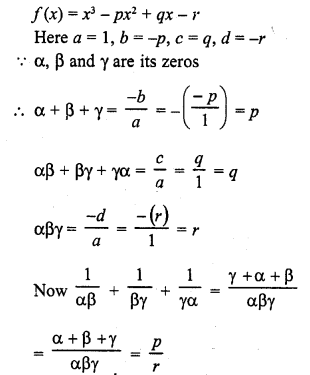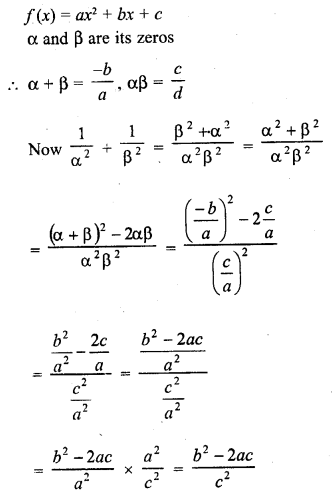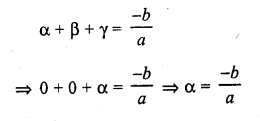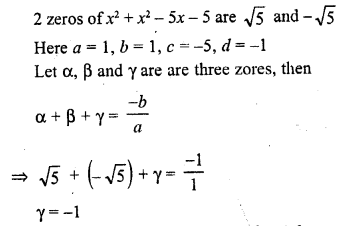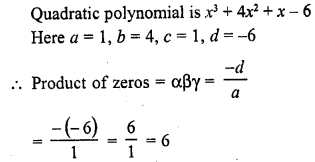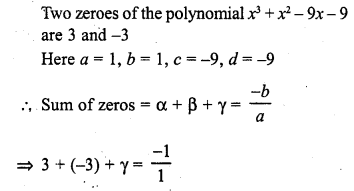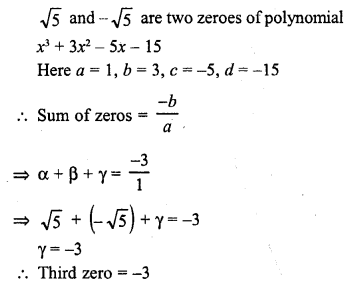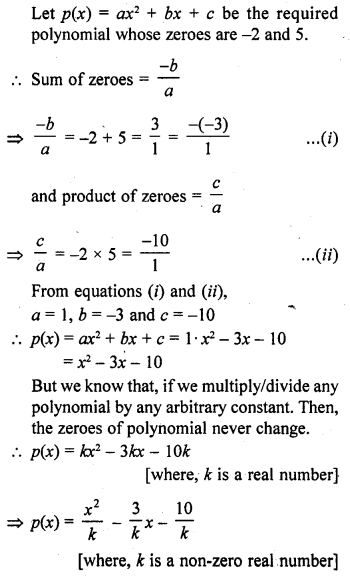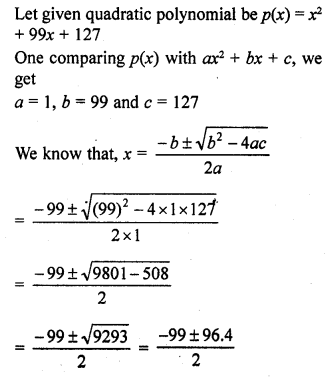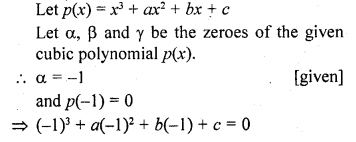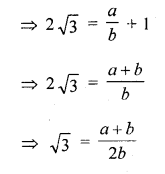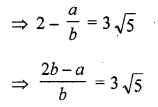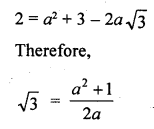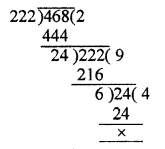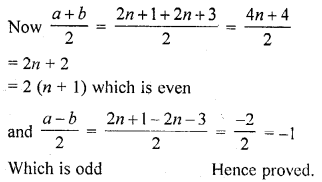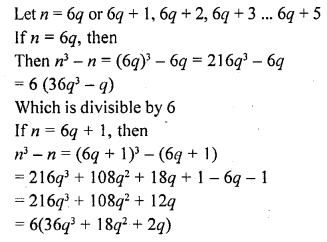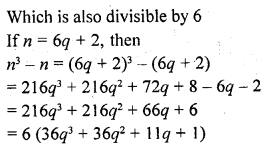RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2
Other Exercises
- RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1
- RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2
- RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.3
- RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS
- RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS
Question 1.
Verify that numbers given along side of the cubic polynomials below are their zeros. Also, verify the relationship between the zeros and coefficients in each case :
(i) f(x) = 2x3 – x2 – 5x + 2 ; \(\frac { 1 }{ 2 }\) , 1, -2
(ii) g(x) = x3 – 4x2 + 5x – 2 ; 2, 1, 1
Solution:
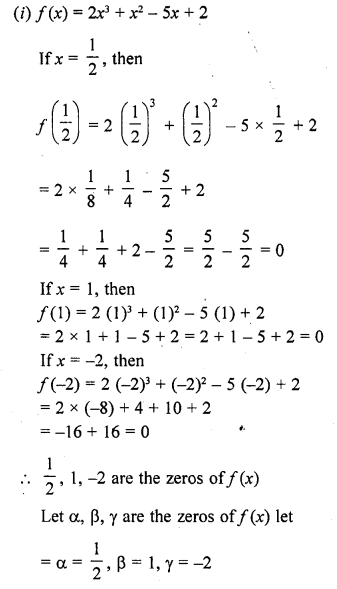


Question 2.
Find a cubic polynomial with the sum, sum of product of its zeros taken two at a time and product of its zeros as 3, -1 and -3 respectively.
Solution:
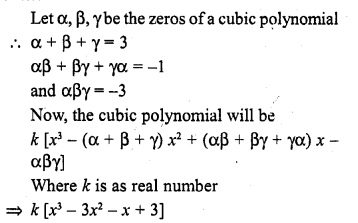
Question 3.
If the zeros of the polynomial f(x) = 2x3 – 15x2 + 37x – 30 are in AP. Find them.
Solution:
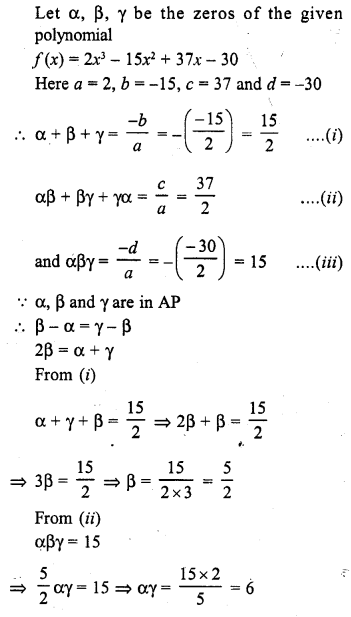
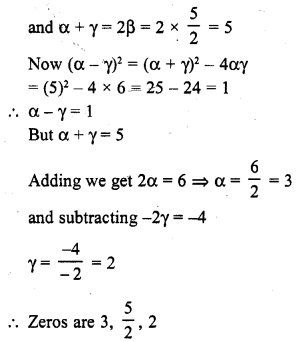
Question 4.
Find the condition that the zeros of the polynomial f(x) = x3 + 3px2 + 3qx + r may be in AP.
Solution:
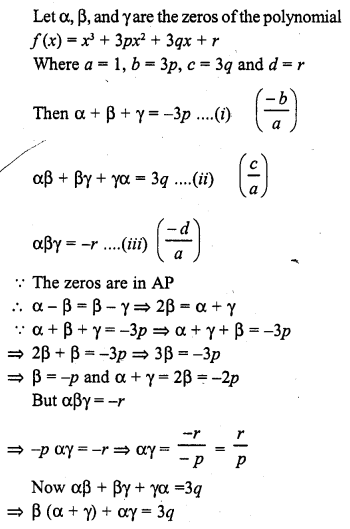
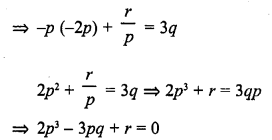
Question 5.
If the zeros of the polynomial f(x) = ax3 + 3bx2 + 3cx + d are in A.P., prove that 2b3 – 3abc + a2d = 0.
Solution:
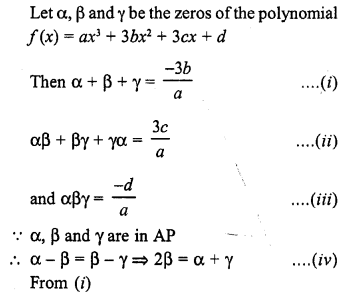
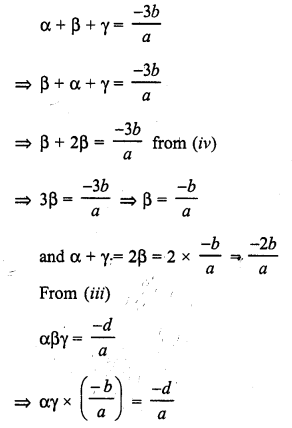
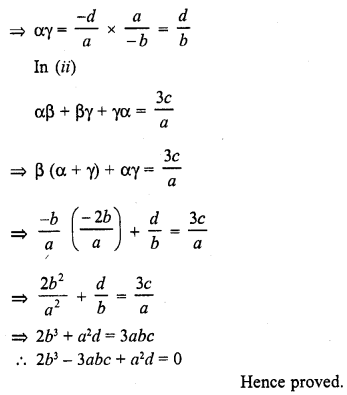
Question 6.
If the zeros of the polynomial f(x) = x3 – 12x2 + 39x + k are in AP, find the value of k.
Solution:
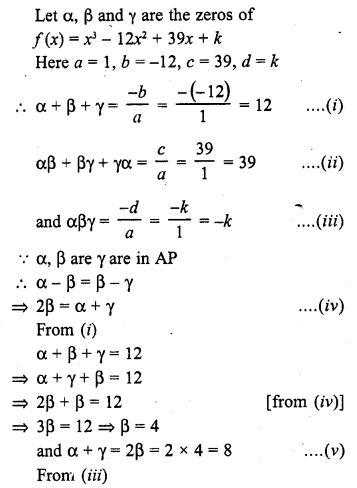
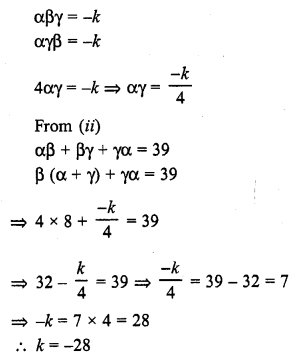
Hope given RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.