Tag: Maths Class 8 RS Aggarwal Solutions

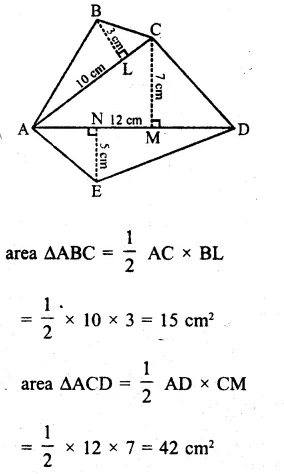
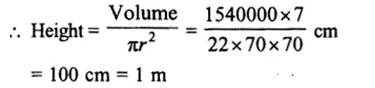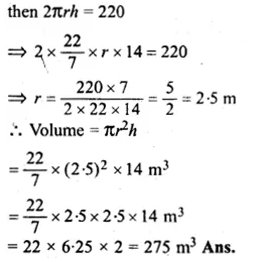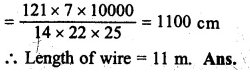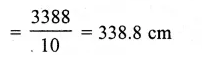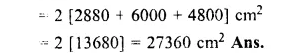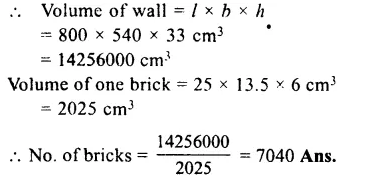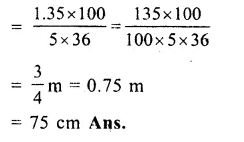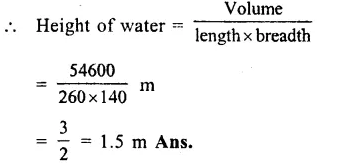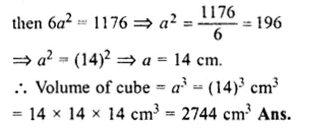RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20C

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20C.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20A
• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20B
• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20C

Tick the correct answer in each of the following:

Question 1.
Solution:
Answer = (b)
Length (l) = 12 cm
Breadth (b) = 9cm
height (h) = 8 cm

Question 2.
Solution:
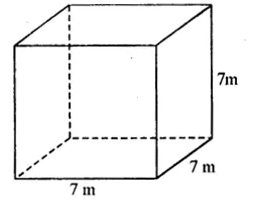
Total surface area of cube = 150 cm²
Side = \( \sqrt { \frac { 150 }{ 6 } } \)
= √25
= 5 cm
Volume = (side)³
= (5)³
= 125 cm³ (b)

Question 3.
Solution:
Volume of cube = 343 cm²
Side = \( \sqrt [ 3 ]{ 343 } =\sqrt [ 3 ]{ 7\times 7\times 7 } \)
= 7 cm
Total surface area = 6 (side)²
= 6 x (7)²
= 6 x 49 cm²
= 294 cm² (c)

Question 4.
Solution:
Rate of painting = 10 paise per cm²
Total cost = Rs. 264.60

Question 5.
Solution:
Answer = (c)
Length of wall (l) = 8m = 800 cm
Breadth (b) = 22.5 cm
Height (h) = 6 m
= 600 cm

Question 6.
Solution:
Answer = (c)
Edge of cube = 10 cm
Volume = a³ = (10)³ = 1000 cm³
Edge of box = 1 m = 100 cm

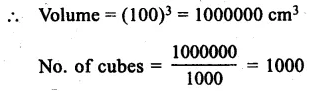
Question 7.
Solution:
Answer = (a)
Ratio in sides of a cuboid = 1 : 2 : 3
Surface area = 88 cm²

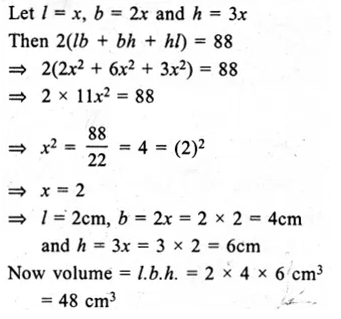
Question 8.
Solution:
Ratio in the two volumes = 1 : 27
Let volume of first volume = x³
and volume of second volume = 27x³
Side of first cube = x

Question 9.
Solution:
Surface area of a brick of measure 10 cm x 4 cm x 3 cm
= 2 (l x b + b x h + h x l)
= 2 [10 x 4 + 4 x 3 + 3 x 10] cm²
= 2 [40 + 12 + 30]
= 82 x 2
= 164 cm² (c)

Question 10.
Solution:
Length of beam (l) = 9 m

Question 11.
Solution:
Water in rectangular reservoir = 42000
Volume = \(\\ \frac { 42000 }{ 1000 } \) = 42 m³
Length (l) = 6 m
Breadth (b) = 3.5 m
Depth = \(\\ \frac { volume }{ l\times b } \)
= \(\\ \frac { 42 }{ 6\times 3.5 } \)
= 2 m (c)

Question 12.
Solution:
Dimensions of a room are 10 m, 8 m, 3.3 m
Volume of air in it = lbh
= 10 x 8 x 3.3 = 264 m³
Air required for one man = 3 m³
No. of men = \(\\ \frac { 264 }{ 3 } \)
= 88 (b)

Question 13.
Solution:
Length of water tank (l) = 3 m
Width (b) = 2 m
and height (h) = 5 m
Volume = lbh = 3 x 2 x 5 = 30 m³
Water in it = 30 x 1000
= 30000 (a)

Question 14.
Solution:
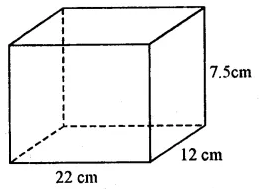
Size of box = 25 cm, 15 cm, 8 cm
Surface area = (lb + bh + hl)
= 2 ( 25 x 15 + 15 x 8 + 8 x 25) cm²
= 2 (375 + 120 + 200) cm²
= 2(695)
= 1390 cm² (b)

Question 15.
Solution:
Diagonal of cube = 4√3
Side = \( \frac { 4\sqrt { 3 } }{ \sqrt { 3 } } \)
= 4 cm
Volume = a³ = (4)³
= 64 cm³ (d)

Question 16.
Solution:
Diagonal of cube = 9√3 cm
Side = \( \frac { 9\sqrt { 3 } }{ \sqrt { 3 } } \)
= 9 cm
Surface area = 6a²
= 6 (9)² = 6 x 81 cm²
= 486 cm² (b)

Question 17.
Solution:
Let side of cube in first case = a
Then volume = a³
If side of cube is doubled, then side = 2a
Volume (2a)³ = 8a³
Becomes 8 times (d)

Question 18.
Solution:
Let side of cube in first case = a
Then surface area = 6a²
and side of second cube = 2a
Surface area = 6 (2a)² = 6 x 4a² = 24a²
Ratio = \(\frac { { 24a }^{ 2 } }{ { 6a }^{ 2 } } \) = 4
Becomes 4 times (b)

Question 19.
Solution:
Sides (edges) of 3 cubes are 6 cm, 8 cm, and 10 cm respectively
Volume of first cube = (6)³ = 216 cm³
Volume of second cube = (8)³ = 512 cm³
and volume of third cube
= (10)³ = 1000 cm³
Sum of volumes of 3 cubes = 216 + 512 + 1000
= 1728 cm³
Volume of new single cube = 1728 cm³
Edge = \(\sqrt [ 3 ]{ 1728 } \)
\(\sqrt [ 3 ]{ { \left( 12 \right) }^{ 3 } } \)
= 12 cm (a)

Question 20.
Solution:
Each edge of 5 cubes = 5 cm
Placing than adjacent to each other
Length of new cuboid (l)
= 5 x 5 = 25 cm
Breadth (b) = 5 cm
and height (h) = 5 cm
Volume of new cuboid = lbh
= 25 x 5 x 5 cm³
= 625 cm³ (d)

Question 21.
Solution:
Diameter of circular well = 2n
Radius = \(\\ \frac { 2 }{ 2 } \) = 1 m
Depth(h) = 14 m
Volume of earth dug out = πr²h
= \(\\ \frac { 22 }{ 7 } \) x 1 x 1 x 14
= 44 m (d)

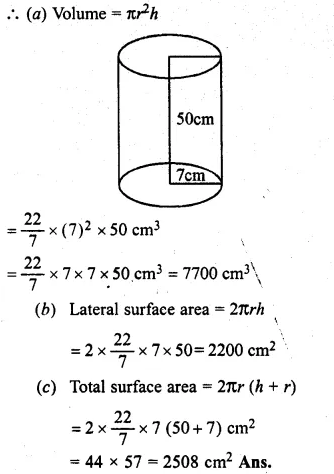
Question 22.
Solution:
Capacity of cylindrical tank = 1848 m³
Diameter = 14 m

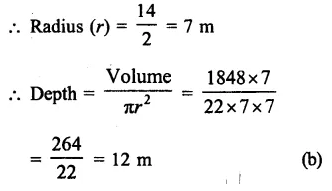
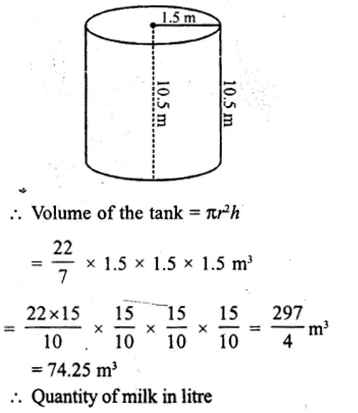
Question 23.
Solution:
Radius of a cylinder (r) = 20 cm
and height (h) = 60 cm

Question 24.
Solution:
Radius of each coin (r) = 0.75 cm
and thickness (h) = 0.2 cm

Question 25.
Solution:
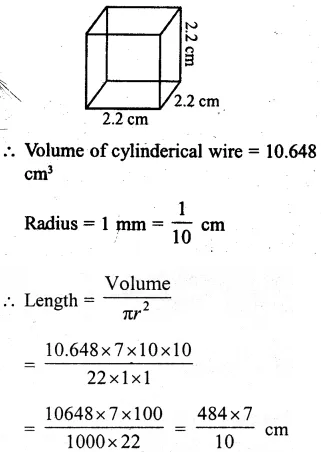
Volume of silver = 66 cm³
Diameter of wire = 1 mm = \(\\ \frac { 1 }{ 10 } \)

Question 26.
Solution:
Diameter of cylinder = 10 cm
Radius (r) = \(\\ \frac { 10 }{ 2 } \) = 5 cm

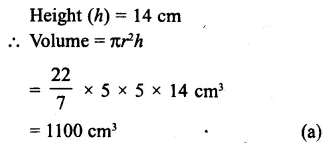
Question 27.
Solution:
Diameter of cylinder = 7 cm
Radius (r) = \(\\ \frac { 7 }{ 2 } \) cm

Question 28.
Solution:
Curved surface area of a cylinder = 264 cm³
Height (h) = 14 cm

Question 29.
Solution:
Diameter of cylinder = 14 cm
Radius (r) = 7 cm
Curved surface area = 220 cm²

Question 30.
Solution:
Ratio in radii of two cylinder = 2 : 3
and ratio in their height = 5 : 3
Let radii of two cylinder = 2x and 3x
and corresponding heights = 5y, 3y

Hope given RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20B.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20A
• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20B
• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20C

Question 1.
Solution:
(i) Radius of the base of the cylinder (r) = 7 cm.
Height (h) = 50 cm.

Question 2.
Solution:
Radius of cylindrical tank (r) = 1.5 m
and height (h) = 10.5 m

= 74.25 x 1000l
= 74250 l

Question 3.
Solution:
Radius of the base of pole (r)
= 10 dm
= \(\\ \frac { 10 }{ 100 } \) m
= \(\\ \frac { 1 }{ 10 } \) m

Question 4.
Solution:
Volume of cylinder = 1.54 m³
= 1540000 cm³
Diameter of its base = 140 cm
Radius (r) = 70 cm

Question 5.
Solution:
Volume of cylindrical rod = 3850 cm³
Length of rod (h) = 1 m = 100 cm
Let radius of the base of the rod = r

Question 6.
Solution:
Diameter of closed cylinder = 14 m
Radius = \(\\ \frac { 14 }{ 2 } \)
= 7 m
Height = 5

Question 7.
Solution:
Circumference of the base of cylinder = 88 cm.

Question 8.
Solution:
Lateral surface of cylinder = 220 m²
Height (h) = 14 m
Let radius of cylinder = r

Question 9.
Solution:
Volume of cylinder = 1232 cm³
height (h) = 8cm
Let r be the radius, then

Question 10.
Solution:
Ratio in radius and height of a cylinder = 7 : 2
Let radius = 7x
then height = 2x

Question 11.
Solution:
Curved surface area = 4400 cm²
circumference of base = 110 cm
Let r be the radius

Question 12.
Solution:
In first case,
Side of square base (a) = 5 cm.
and height (h) = 14 cm.
Volume = 5 x 5 x 14 = 350 cm³
In second case,
Radius of the circular base (r) = 3.5 cm.
Height (h) = 12 cm.
Volume = πr²h
= \(\\ \frac { 22 }{ 7 } \) x 3.5 x 3.5 x 12 cm³
= 462 cm²
Hence second type of circular plastic can has greater capacity.
Difference = 462 – 350
= 112 cm³

Question 13.
Solution:
Diameter of a cylindrical pillar = 48 cm.
Radius (r) = \(\\ \frac { 48 }{ 2 } \) = 24 cm.
\(\\ \frac { 24 }{ 100 } \) m

Question 14.
Solution:
Length of rectangular vessel (l) = 22 cm.
Breadth (A) = 16 cm.
and height (A) = 14 cm.

Question 15.
Solution:
Diameter of cylindrical metal = 1 cm.
Radius (r) = \(\\ \frac { 1 }{ 2 } \) cm.
Length. (A) = 11 cm.
Volume = πr²h

Question 16.
Solution:
Side of a solid cube = 2.2 cm
Volume = (side)³
= (2.2)³
= 10.648 cm³

Question 17.
Solution:
Diameter of a well = 7 m
Radius (r) = \(\\ \frac { 7 }{ 2 } \) m

Question 18.
Solution:
Inner diameter of well = 14 m
Inner radius = \(\\ \frac { 14 }{ 2 } \) = 7 m
Depth (h) = 12 m

Question 19.
Solution:
No. of revolutions = 750
Diameter of road roller = 84 cm
Length (h) = 1 m

Question 20.
Solution:
Thickness of the metal = 1.5 cm.
External diameter = 12 cm.

Question 21.
Solution:
Inner diameter of tube = 12 cm.
Inner radius (r) = \(\\ \frac { 12 }{ 2 } \) = 6 cm.
Thickness of metal = 1 m.

Hope given RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 20 Volume and Surface Area of Solids Ex 20A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20A.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20A
• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20B
• RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20C

Question 1.
Solution:
(i)

Length of cuboid (l) = 22 cm.
Breadth (b) = 12 cm
and height (h) = 7.5 cm.

Question 2.
Solution:
Length of water tank (l) = 2 m
75cm = 2.75 m
breadth (b) = 1 m 80cm = 1.80 m
and height (h) = 1 m 40 cm = 1.40 m
Volume of water filled in it = l.b.h = 2.75 x 1.80 x 1.40 m³
= 6.93 m³
Water in litres = 6.93 x 1000
= 6930 litres (1 m³ = 1000 litres) Ans.

Question 3.
Solution:
Length of iron (l) = 1.05 m
= 105 cm
breadth (b) = 70 cm and height (h) = 1.5 cm
volume of iron = l x b x h = 105 x 70 x 1.5 cm³
= 11025 cm³
weight of 1cm³ iron = 8 gram
Total weight = 11025 x g = 88200 g
= \(\\ \frac { 88200 }{ 1000 } \) kg
= 88.2 kg Ans.

Question 4.
Solution:
Area of courtyard = 3750 m²
Height of gravel = 1 cm.
Volume of gravel = 3750 x \(\\ \frac { 1 }{ 100 } \) m³
= 37.50 m³
Cost of 1 m³ gravel = Rs. 6.40
Total cost = Rs. 6.40 x 37.50
= Rs. 240 Ans.

Question 5.
Solution:
Length of hall (l) = 16 m
Breadth (b) = 12.5 m
height (h) = 4.5 m
Volume of air in it = l x b x h
= 16 x 12.5 x 4.5 m3
= 900 m³
Air for one person is required = 3.6 m³
Number of person which can be accommodated in the hall = 900 ÷ 3.6
= \(\\ \frac { 900\times 10 }{ 36 } \)
= 250

Question 6.
Solution:
Length of cardboard box (l)
= 1.2 m = 120 cm.
breadth (b) = 72 cm.
Height (h) = 54 cm.
Volume of box = l x b x h
= 120 x 72 x 54 cm³
= 466560 cm³
Volume of one soap bar = 6 x 4.5 x 4 cm³
= 108 cm³
No. of bars to be kept in it = \(\\ \frac { 466560 }{ 108 } \)
= 4320 Ans.

Question 7.
Solution:
Volume of one match box = 4 x 2.5 x 1.5 cm³ = 15 cm³
Volume of 144 matchboxes = 15 x 144 cm³
or volume of one packet = 2160 cm³
Length of carton (l) = 1.5 m = 150 cm
Breadth (b) = 84 cm
and height (h) = 60 cm.
Volume of one carton = l x b x h
= 150 x 84 x 60 cm³
= 756000 cm³
No. of packets = 756000 ÷ 2160
= 350 Ans.

Question 8.
Solution:
Length of one plank = 2m
= 200 cm
Breadth (b) = 25 cm

Question 9.
Solution:
Length of wall (l) = 8m = 800 cm
Height (h) = 5.4 m = 540 cm
Width (b) = 33 cm

Question 10.
Solution:
Length of wall (l) = 15 m
Width (b) = 30 cm = 0.3 m
Height (h) = 4 m

Question 11.
Solution:
Length of rectangular cistern (l) = 11.2 m
Breadth (b) = 6 m
Height (h) = 5.8 m

Question 12.
Solution:
Volume of block of gold = 0.5 m³
= 0.5 x 1000000 cm³
= 500000 cm³

Question 13.
Solution:
Area of field = 2 hectare
= 20000 m²
Rainfall = 5 cm. = 0.05 m
Volume of water of rainfall
= Area of field x height of rainfall water
= 20000 x 0.05 m³
= 1000 m³ Ans.

Question 14.
Solution:
Speed of water = 3 km/h
Length of water flow in 1 minute
= \(\\ \frac { 3km }{ 60m } \)
= \(\\ \frac { 3000 }{ 60 } \)
= 50 m
Width of river = 45 m
Depth of river = 2 m
Volume of water in 1 minute
= 45 x 2 x 50 m³
= 4500 m³ Ans.

Question 15.
Solution:
Length of pit (l) = 5m
Width (b) = 3.5 m
Let depth of pit = h
then volume of earth dug out
= l.b.h = 5 x 3.5 x h = 17.5 h m³
But volume of earth = 14 m³
17.5 h = 14
h = \(\\ \frac { 14 }{ 17.5 } \) = \(\\ \frac { 140 }{ 175 } \)
=> h = \(\\ \frac { 4 }{ 5 } \) m
= \(\\ \frac { 4 }{ 5 } \) x 100
= 80 cm Ans.

Question 16.
Solution:
Width of tank = 90 cm = \(\\ \frac { 90 }{ 100 } \) m
Depth = 40 cm = \(\\ \frac { 40 }{ 100 } \) m
Water = 576 litre

Question 17.
Solution:
Volume of wood = 1.35 m³
Length of beam = 5m
Thickness = 36 cm = \(\\ \frac { 36 }{ 100 } \) m.
Width = \(\\ \frac { Volume }{ length\times thickness } \)

Question 18.
Solution:
Volume of a room = 378 m³
Area of its floor = 84 m²
Height = \(\\ \frac { Volume }{ Area } \)
= \(\\ \frac { 378 }{ 84 } \) m
= 4.5 m Ans.

Question 19.
Solution:
Length of pool = 260 m
and width = 140 m.
Volume of water = 54600 m³

Question 20.
Solution:
Outer length of wooden box (L) = 60 cm
Width (B) = 45 cm
and height (H) = 32 cm.
Thickness of wood used = 2.5 cm.
Inner length (l) = 60 – 2 x 2.5
= 60 – 5
= 55 cm

Question 21.
Solution:
Outer length of open box = 36 cm
breadth = 25 cm
and height = 16.5 cm
thickness of iron = 1.5 cm.
∴ Inner length = 36 – 2 x 1.5
= 36 – 3
= 33 cm
breadth = 25 – 2 x 1.5
= 25 – 3
= 22 cm
and height = 16.5 – 1.5
= 15 cm .
∴ Volume of iron used in it = Outer volume – Inner volume
= 36 x 25 x 16.5 cm3 – 33 x 22 x 15 cm³
= 14850 – 10890
= 3960 cm³
weight of 1 cm³ = 8.5 gram
∴ Total weight = 3960 x 8.5 g
= 33660 g
= 33.660 kg
= 33.66 kg Ans.

Question 22.
Solution:
Outer length of the box = 56 cm
Width = 39 cm
and height = 30 cm
Volume = 56 x 39 x 30
= 65520 cm³
Thickness of wood used = 3cm.
∴ Inner length = 56 – 2 x 3
= 56 – 6
= 50 cm
Width = 39 – 2 x 3
= 39 – 6
= 33 cm
and height = 30 – 2 x 3
= 30 – 6
= 24 cm
∴ Inner volume of the box = 50 x 33 x 24 cm³
= 39600 cm³
and volume of wood used = Outer volume – Inner volume
= (65520 – 39600)cm³
= 25920 cm³ Ans.

Question 23.
Solution:
Outer length of box = 62 cm.
Outer width = 30 cm.
Outer height = 18 cm.
Thickness of wood = 2 cm.
∴ Internal length = 62 – 2 x 2
= 58 cm.
Internal width = 30 – 2 x 2
= 26 cm.
Internal height =18 – 2 x 2
= 14 cm.
Capacity of the box = lbh
= 58 x 26 x 14 cm³
= 21112 cm³ Ans.

Question 24.
Solution:
Outer length = 80 cm.
Outer width = 65 cm.
Outer height = 45 cm.
Total volume = 80 x 65 x 45 cm³
= 234000 cm³
Thickness of wood = 2.5 cm.
∴ Inner length = 80 – 2 x 2.5 = 75 cm.
Inner width = 65 – 2 x 2.5 = 60 cm.
Inner height = 45 – 2 x 2.5 = 40 cm.

Question 25.
Solution:
(i) Edge of cube (a) = 7 m

(a) Volume = a³ = (7)³
= 7 x 7 x 7 m³
= 343 m³ Ans.

Question 26.
Solution:
Surface area of a cube = 1176 cm²
Let edge of the cube = a

Question 27.
Solution:
Volume of a cube = 729 cm³
Let edge of cube = a
then a³ = 729 = (9)³
a = 9 cm.
Hence surface area = 6a² = 6 (9)² cm²
= 6 x 81
= 486 cm² Ans.

Question 28.
Solution:
Length of metal block (l) = 2.25 m = 225 cm
Width (b) = 1.5 m = 150 cm
and height (h) = 27 cm
Volume of block = l x b x h
= 225 x 150 x 27 cm³
= 911250 cm³
Side of each cube = 45 cm.
Volume of each cube = a³
= 45 x 45 x 45
= 94125 cm³
Number of cubes = \(\\ \frac { 911250 }{ 91125 } \)
= 10 Ans.

Question 29.
Solution:
Let edge of given cube = a
Volume = a³
and surface area = 6a²
By doubling the edge of cube3 the side of new cube = a x 2 = 2a
Volume (2a)³ = 8a³
and surface area = 6 (2a)² = 6 x 4a²
= 24a² = 4 x 6a²
It is clear from the above that
Volume is increased 8 times and surface area is 4 times. Ans.

Question 30.
Solution:
Total cost of wood = Rs. 256
Rate = Rs.,500 per m³
Volume of wood = \(\\ \frac { 256 }{ 500 } \) = 0.512 m³
= 0.512 x 100 x 100 x 100 cm³
= 512000 cm³
Let length of each side = a
then a³ = 512000 = (80)³
a = 80
Hence length of each side = 80 cm. Ans.

 

Hope given RS Aggarwal Solutions Class 8 Chapter 20 Volume and Surface Area of Solids Ex 20A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 19 Three-Dimensional Figures Ex 19B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 19 Three-Dimensional Figures Ex 19B.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 19 Three-Dimensional Figures Ex 19A
• RS Aggarwal Solutions Class 8 Chapter 19 Three-Dimensional Figures Ex 19B

Question 1.
Solution:
Euler’s Relation
= F – E + V = 2
Where F is no. of faces
E is no. of edges
V is no. of vertices

Question 2.
Solution:
Edges of
(i) Cuboid are 12
(ii) Tetrahedron are 6
(iii) Triangular prism are 9
(iv) Square pyramid are – 8

Question 3.
Solution:
Faces of
(i) Cube are 6
(ii) Pentagonal prism are 7 (5 + 2)
(iii) Tetrahedron are 4
(iv) Pentagonal pyramid are 6

Question 4.
Solution:
Vertices of
(i) Cuboid are 8
(ii) Tetrahedron are 4
(iii) Pentagonal prism are 10
(iv) Square pyramid are 5

Question 5.
Solution:
(i) A cube
F – E + V = 2
=> 6 – 12 + 8 = 2
=> 14 – 12 = 2
=> 2 = 2
(ii) A tetrahedron
F – E + V = 2
=> 4 – 6 + 4 = 2
=> 8 – 6 = 2
=> 2 = 2
(iii) A triangular prism
F – E + V = 2
=> 5 – 9 + 6 = 2
=> 11 – 9
=> 2 = 2
(iv) A square pyramid
F – E + V = 2
=> 5 – 8 + 5 = 2
=> 10 – 8 = 2
=> 2 = 2

Hope given RS Aggarwal Solutions Class 8 Chapter 19 Three-Dimensional Figures Ex 19B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 19 Three-Dimensional Figures Ex 19A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 19 Three-Dimensional Figures Ex 19A.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 19 Three-Dimensional Figures Ex 19A
• RS Aggarwal Solutions Class 8 Chapter 19 Three-Dimensional Figures Ex 19B

Question 1.
Solution:
(i) Cuboid : It has 6 faces.
(ii) Cube : It has 6 faces.
(iii) Triangular prism : It has 5 faces.
(iv) Square Pyramid : It has 5 faces.
(v) Tetrahedron : It has 4 faces. Ans.

Question 2.
Solution:
(i) Tetrahedron : It has 6 edges.
(ii) Rectangular pyramid : It has 8 edges
(iii) Cube : It is 12 edges.
(iv) Triangular prism : It has 9 edges Ans.

Question 3.
Solution:
(i) Cuboid : It has 8 vertices
(ii) Square pyramid : It has 5 vertices.
(iii) Tetrahedron : It is 4 vertices.
(iv) Triangular prism : It has 6 vertices

Question 4.
Solution:
(i) A cube has 8 vertices 12 edges and 6 faces.
(ii) The point at which three faces of a figure meet is known as vertex.
(iii) A cuboid is also known as a rectangular prism.
(iv) A triangular pyramid is called a tetrahedron.

 

Hope given RS Aggarwal Solutions Class 8 Chapter 19 Three-Dimensional Figures Ex 19A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18C

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18C.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18A
• RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18B
• RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18C

Tick the correct answer in each of the following :

Question 1.
Solution:
Parallel sides 14 cm and 18 cm
Distance between parallel sides (h) = 9cm

Question 2.
Solution:
Length of parallel sides are 19 cm and 13 cm
Area of trapezium = 128 cm²
Distance between then

Question 3.
Solution:
Ratio in parallel sides = 3:4
Perpendicular distance (h) = 12 cm
Area of trapezium = 630 cm²

Question 4.
Solution:
Area of trapezium = 180 cm²
and height (h) = 9 cm

Question 5.
Solution:
In the figure, AB || DC, DA ⊥ AB
DC = 7 cm, BC = 10 cm, AB = 13 cm
CL ⊥ AB
AD = DC = 7 cm
and LB – 13 – 7 = 6 cm

Hope given RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18B.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18A
• RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18B
• RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18C

Question 1.
Solution:
In quad. ABCD
AC = 24 cm, BL ⊥ AC and DM ⊥ AC
BL = 8 cm and DM = 7 cm

Question 2.
Solution:
In quad. ABCD, diagonal BD = 36 m
AL ⊥ BD and CM ⊥ BD
AL = 19 m and CM = 11 m

Question 3.
Solution:
In the given pentagon ABCDE,
BL ⊥ AC, DM ⊥ AC, EN ⊥ AC
AC = 18 cm, AM = 14 cm, AN = 6 cm,
BL = 4 cm, DM = 12 cm and EN = 9 cm

Question 4.
Solution:
In hexagon ABCDEF, there are triangles and trapeziums
AP = 6 cm, PL = 2 cm, LN = 8 cm,
NM = 2 cm, MD = 3 cm, FP = 8 cm,
EN = 12 cm, BL = 8 cm and CM = 6 cm

Question 5.
Solution:
In the given pentagon ABCDE,
BL ⊥ AC, CM ⊥ AD, EN ⊥ AD
AC = 10 cm, D = 12 cm, BL = 3 cm,
CM = 7 cm and EN = 5 cm

Question 6.
Solution:
In the figure, ABCF is 0 square and CDEF is a trapezium
Now area of sq. ABCF
= (side)² = (20)² = 400 cm²
area of trap. CDEF
= \(\\ \frac { 1 }{ 2 } \) (ED + FC ) x height

Question 7.
Solution:
In the right ∆ABC
AB² = BC² + AC²
=> (5)² = (4)² + AC²
25 = 16 + AC²
AC² = 25 – 16 = 9 = (3)²
AC = 3 cm

= 32 + 36
= 68 cm²

Question 8.
Solution:
AD = 23 cm, LM = 13 cm
AL = MD = \(\\ \frac { 23-13 }{ 2 } \) = \(\\ \frac { 10 }{ 2 } \) = 5 cm

Hope given RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 23 Pie Charts Ex 23A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 23 Pie Charts Ex 23A.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 23 Pie Charts Ex 23A
• RS Aggarwal Solutions Class 8 Chapter 23 Pie Charts Ex 23B

Question 1.
Solution:
Total expenditure = Rs. 4000 + 5400 + 2800 + 1800 + 400 = Rs. 14400

Construction of pie chart :
1. Draw a circle of any convenient radius.
2. Draw a horizontal radius.
3. Staring from this radius, draw sectors of central angle 100°, 135°, 70°, 45° and 10° respectively.
4. Shade these sectors with different colors or designs as shown in the figure.
This is the required pie chart.

Question 2.
Solution:
Total number of creatures 900

(i) Draw a circle with a suitable radius.
(ii) Draw a horizontal radius.
(iii) Starting from this radius, draw sectors whose central angles are 60°, 160°, 70°, 50° and 20° respectively.
(iv) Now shade each sector with different colours or designs as shown in the figure.

Question 3.
Solution:
Total number of students = 350 + 245 + 210 + 175 + 280 = 1260

(i) Draw a circle with a suitable radius.
(ii) Draw a horizontal radius.
(iii) Starting from this radius draw sectors whose central angles are 100°, 70°, 60°, 50° and 80° respectively.
(iv) Now shade each sector with different colours or designs as shown in the figure.

Question 4.
Solution:

(i) Draw a circle with a suitable radius.
(ii) Draw a horizontal radius.
(iii) Starting from this radius, draw sectors whose actual angles are 105°, 60°, 30°, 120° and 45° respectively.
(iv) Now shade each sector with different colours or design as shown in the figure.

Question 5.
Solution:
Here total number of workers = 1080

Now (i) Draw a circle with a suitable radius
(ii) Draw a horizontal radius
(iii) Starting from this radius, draw sectors whose central angle are 150°, 90°, 85°, 35° respectively.
(iv) Now shade the sectors with different colours or designs as shown in the figure.

Question 6.
Solution:
Total marks obtained by Sudhir
= 105 + 75 + 150 + 120 + 90 = 540

(i) Draw a circle with a suitable radius
(ii) Draw a horizontal radius
(iii) Starting from this radius, draw sectors whose central angles are 70°, 50°, 100°, 80° and 60° respectively
(iv) Now shade these sectors with different colours or designs as shown in the figure.

Question 7.
Solution:
Total number of fruits = 26 + 30 + 21 + 5 + 8 = 90

(i) Draw a circle with a suitable radius.
(ii) Draw a horizontal radius.
(iii) Starting from this radius, draw sectors of central angles 104°, 120°, 84°, 20° and 32° respectively.
(iv) Shade these sectors with different colours or designs as shown in the figure.

Question 8.
Solution:
Total number of million of tonnes of food grains = 57 + 76 + 38 + 19 = 190 million of tonnes

(i) Draw a circle with suitable radius.
(ii) Draw a horizontal radius.
(iii) Starting with this radius, draw sectors of central angles 108°, 144°, 72° and 366 respectively.
(iv) Shade these sectors with different colours or designs as shown in the figure.

Question 9.
Solution:
Total percentage = 25 + 45 + 20 + 10 = 100%

(i) Draw a circle with a suitable radius.
(ii) Draw a horizontal radius.
(iii) Starting from this radius, draw sectors of central angles 90°, 162°, 72° and 36° respectively.
(iv) Shade these sectors with different colours or designs as shown in the figure.

Question 10.
Solution:
Total percentage = 20 + 40 + 25 + 15 = 100%

(i) Draw a circle with a suitable radius.
(ii) Draw a horizontal radius.
(iii) Starting from this radius, draw sectors of central angles 72°, 144°, 90° and 54° respectively.
(iv) Now shade these sectors with different colours or designs as shown in the figure.

 

Hope given RS Aggarwal Solutions Class 8 Chapter 23 Pie Charts Ex 23A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 18 Area of a Trapezium and a Polygon Ex 18A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18A.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18A
• RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18B
• RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18C

Question 1.
Solution:
In trapezium ABCD,
Length of parallel sides
AB = 24 cm, DC = 20 cm
and distance between them = 15 cm

Question 2.
Solution:
Parallel sides of a trapezium ABCD are
l1 = 38.7 cm. and l2 = 22.3 cm

Question 3.
Solution:
Parallel sides of the trapezium = 1 m, 1.4 m

Question 4.
Solution:
Area of trapezium = 1080 cm²
Lengths of parallel sides are
l1 = 55 cm and l2 = 35 cm
Let h be the distance between them

Question 5.
Solution:
Area of trapezium shaped field = 1586m²
Distance between parallel sides = 26 m
Sum of the parallel sides = \(\frac { Area\times 2 }{ Altitude }\)
= \(\frac { 1586\times 2 }{ 26 } \) = 122 m
One side = 84 m
Second side = 122 – 84
= 38 m

Question 6.
Solution:
Area of trapezium = 405 cm²
Ratio in parallel sides = 4:5
and distance between them = 18 cm

Question 7.
Solution:
Area of trapezium = 180 cm²
Height (h) = 9 cm.
Let l1 and l2 be the parallel sides,

Question 8.
Solution:
Let one of parallel sides = x
Then second sides = 2x
Area = 9450 m²
Distance between them = 84 m

Question 9.
Solution:
Perimeter of trapezium ABCD = 130 m
AB ⊥ AD and BC
BC = 54 m, CD = 19 m, AD = 42 m

Question 10.
Solution:
In the given trapezium ABCD, AC is

Question 11.
Solution:
In trapezium ABCD,

Question 12.
Solution:
In trapezium ABCD,

AB || DC
AB = 25 cm DC = 1 cm
AD = 13 cm and BC = 15 cm

 

Hope given RS Aggarwal Solutions Class 8 Chapter 18 Area of a Trapezium and a Polygon Ex 18A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 17 Construction of Quadrilaterals Ex 17B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 17 Construction of Quadrilaterals Ex 17B.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 17 Construction of Quadrilaterals Ex 17A
• RS Aggarwal Solutions Class 8 Chapter 17 Construction of Quadrilaterals Ex 17B

Question 1.
Solution:
Steps of Construction :

(i) Draw a line segment AB = 5.2 cm.
(ii) With centre A and radius 7.6 cm. and with centre B and radius 4.7 cm. draw arcs which intersect each other at C.
(iii) Join AC and BC.
(iv) Again with centre A and radius 4.7 cm and with centre C and radius 5.2 cm draw arcs which intersect each other at D.
(v) Join AD and CD.
ABCD is the required parallelogram.

Question 2.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 4.3 cm.

(ii) With centre A and radius 4 cm. and with centre B and radius 6.8 cm., draw arcs which intersect each other at D.
(iii) Join AD and BD.
(iv) Again with centre B and radius 4 cm. and with centre D and radius 4.3 cm., draw arcs intersecting each other at C.
(v) Join DC and BC. ABCD is the required parallelogram.

Question 3.
Solution:
Steps of Construction :
(i) Draw a line segment PQ = 4 cm.
(ii) At Q, draw a ray making an angle of 60° and cut off QR = 6 cm.

(iii) With centre P and radius 6 cm. and with centre R and radius 4 cm draw arcs intersecting each other at S.
(iv) Join RS and PS.
PQRS is the required parallelogram. Q.

Question 4.
Solution:
Steps of Construction :
(i) Draw a line segment BC = 5 cm.

(ii) At C, draw a ray making an angle of 120° and cut off CD = 4.8 cm.
(iii) With centre B and radius 4.8 cm. with centre D and radius 5 cm, draw arcs intersecting each other at A.
(iv) Join AB and AD
ABCD is the required parallelogram.

Question 5.
Solution:
Steps of Construction :
We know that diagonals of a parallelogram bisect each other.
(i) Draw a line segment AB = 4.4 cm.
(ii) With centre A and radius \(\\ \frac { 5.6 }{ 2 } \) cm and with centre B and radius \(\\ \frac { 7 }{ 2 } \) = 3.5 cm. draw arcs
intersecting each other at O.
(iii) Join AO and BO and produce them to C and D respectively such that OC = 2.8 cm and OD = 3.5 cm.

(iv) Join AD, CD and BC
ABCD is the required parallelogram

Question 6.
Solution:
Steps of Construction :

(i) Draw a line segment AB = 6.5 cm.
(ii) At A, draw a perpendicular AX and cut off AL = 2.5 cm.
(iii) Through L, draw a line PQ parallel to AB.
(iv) From A, draw an arc of radius 3 -4 cm which intersects the line PQ at C.
(v) Join AC. BC
(vi) From PQ, cut off CD = AB.
(vii) Join AD
(viii) From C, draw a perpendicular CM to AB.
ABCD is the required parallelogram.

Question 7.
Solution:
Steps of Construction :

(i) Draw a line segment AC = 3.8 cm.
(ii) Bisect it at O.
(iii) At O, draw a ray making an angle of 60° and produce it both sides.
(iv) From O cut off OB = OD = 2.3 cm.
(v) Join AB, BC, CD and AD.
ABCD is the required parallelogram.

Question 8.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 11 cm.

(ii) At B, draw a perpendicular and cut off BC = 8.5 cm.
(iii) With centre A and radius 8.5 cm and with centre C and radius 11 cm, draw arcs intersecting each other at D.
(iv) Join AD and CD.
ABCD is the required rectangle.

Question 9.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 6.4 cm.

(ii) At A and B draw perpendiculars and
cut off AD = BC = AB = 6.4 Cm.
(iii) Join CD.
ABCD is the required square.

Question 10.
Solution:
Steps of Construction :
(i) Draw a line segment AC = 5.8 cm.

(ii) Draw its perpendicular bisector intersecting AC at O.
(iii) From O, cut off OD = OB = 2.9 cm.
\(\qquad =\left( \frac { 1 }{ 2 } BD \right) \)
(iv) Join AB, BC, CD and DA. ABCD is the required square.

Question 11.
Solution:
Steps of Construction :

(i) Draw a line segment QR = 3.6 cm.
(ii) At Q, draw a ray QX making an angle of 90°.
(iii) With centre R and radius 6 cm. draw an arc which intersects QX at P.
(iv) Join PR.
(v) With centre P and radius equal to QR and with centre R and radius equal to QP, draw arcs intersecting each other at S.
(vi) Join PS and RS.
PQRS is the required rectangle.
The length of other side PQ = 4.8 cm.

Question 12.
Solution:
Steps of Construction :

(i)Draw a line segment AC = 8 cm.
(ii)Draw its perpendicular bisector intersecting it at O.
(iii)From O, cut off OB = OD = 3 cm.
(iv)Join AB, BC, CD and DA.
ABCD is the required rhombus.

Question 13.
Solution:
Steps of Construction :
(i)Draw a line segment AC = 6.5 cm.

(ii) With centres A and C and radius equal to 4 cm., draw arcs which intersect each other on both sides of line segment AC at B and D respectively.
(iii) Join AB, BC, CD and DA.
ABCD is the required rhombus.

Question 14.
Solution:
Steps of Construction :

(i)Draw a line segmentAB = 7.2 cm.
(ii)At A draw a ray AX making an angle of 60° and cut off AD = 7.2 cm.
(iii)With centres D and B, and radius 7.2 cm., draw arcs intersecting each other at C.
(iv)Join CD and CB.
ABCD is the required rhombus.

Question 15.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 6 cm

(ii)At B, draw a ray BX making an angle of 75° and cut off BC = 4 cm.
(iii) At C, draw a ray CY making an angle of 180° – 75° = 105°
So that CY may be parallel to AB.
(iv) From CY, Cut off CD = 3.2 cm.
(v) Join DA.
ABCD is the required trapezium.

Question 16.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 7 cm.

(ii) At B, draw a ray BX making an angle of 60° and cut off BC = 5 cm.
(iii) At C, draw a ray CY making an angle of (180° – 60°) = 120° so that CY || AB.
(iv) With centre A and radius 6.5 cm. draw an arc intersecting CY at D.
(v) Join AD,
ABCD is the required trapezium.

Hope given RS Aggarwal Solutions Class 8 Chapter 17 Construction of Quadrilaterals Ex 17B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 8 Solutions Chapter 17 Construction of Quadrilaterals Ex 17A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 17 Construction of Quadrilaterals Ex 17A.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 17 Construction of Quadrilaterals Ex 17A
• RS Aggarwal Solutions Class 8 Chapter 17 Construction of Quadrilaterals Ex 17B

Question 1.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 4.2 cm.

(ii) With centre A and radius 8 cm and with centre B and radius 6 cm., draw arcs intersecting each other at C.
(iii) Join AC and BC.
(iv) Again with centre A and radius 5 cm. and with centre C, radius 5 2 cm. draw arcs intersecting each other at D.
(v) Join AD and CD. ABCD is the required quadrilateral.

Question 2.
Solution:
Steps of Construction :
(i) Draw a line segment PQ = 5.4 cm.

(ii) With Centre P and radius 4 cm. and with centre Q and radius 4.6 cm., draw arcs intersecting each other at R.
(iii) Join PR and QR.
(iv) Again with centre P and radius 3.5 cm. and with centre R and radius 4.3 cm. draw arcs intersecting each other at S.
(v) Join PS and RS. PQRS is the required quadrilateral.

Question 3.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 3.5 cm.

(ii) With centre A and radius 4.5 cm. and with centre B and radius 5.6 cm. draw arcs intersecting each other at D.
(iii) Join AD and BD.
(iv) With centre B and radius 3.8 cm. and with centre D and radius 4.5 cm., draw arcs intersecting each other at C.
(v) Join BC and DC. ABCD is the required quadrilateral.

Question 4.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 3.6 cm.
(ii) With centre A and radius 4.6 cm. and with centre B and radius 3.3 cm. draw arcs intersecting each other at C.

(iii) Join AC and BC.
(iv) Again with centre A and radius 2.7 cm. and centre B and radius 4 cm., draw arcs intersecting each other at D.
(v) Join BD, AD and CD. ABCD is the required quadrilateral.

Question 5.
Solution:
Steps of Construction :
(i) Draw a line segment RS = 5 cm.
(ii) With centre R and S, radius 6 cm. each, draw arcs intersecting each other at R
(iii) Join PR and PS.

(iv) With centre R and radius 7.5 cm. and with centre S and radius 10 cm, draw arcs intersecting each other at Q.
(v) Join RQ, SQ and PQ. PQRS is the required quadrilateral. Measuring the fourth sides PQ, it is 4.7 cm. (approx.)

Question 6.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 3.4 cm.

(ii) With centre A and radius 5.7 cm. and with centre B and radius 4 cm., draw arcs intersecting each other at D.
(iii) Join BD and AD.
(iv) Again with centre A and radius 8 cm and with centre D and radius 3 cm., draw arcs intersecting each other at C.
(v) Join AC, BC and DC. ABCD is the required quadrilateral

Question 7.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 3.5 cm.

(ii) At B, draw a ray BX making an angle of 120° using protractor and cut off BC = 3.5 cm
(iii) With centres A and C and radius 5.2 cm, draw arcs intersecting each other at D.
(iv) Join CD and AD. ABCD is the required quadrilateral.

Question 8.
Solution:
Steps of Construction :
(i) Draw a line AB = 2.9 cm.
(ii) At A, draw a ray AX making an angle of 70° with AB. Using protractor and cut off AD = 3.4 cm.

(iii) With centre B and radius 3.2 cm and with centre D and radius 2.7 cm., draw arcs intersecting each other at C.
(iv) Join BC and DC. ABCD is the required quadrilateral.

Question 9.
Solution:
Steps of Construction

(i) Draw a line segment BC = 5 cm.
(ii) At B, draw a ray BX making an angle of 125° and cut off BA = 3.5 cm.
(iii) At C, draw a ray CY making an angle of 60° and cut off CD = 4.6 cm
(iv) Join AD. ABCD is the required quadrilateral.

Question 10.
Solution:
Steps of Construction :
(i) Draw a line segment QR = 5.6 cm.

(ii) At Q, draw a ray QX making an angle of 45° and cut off QP = 6 cm.
(iii) At R, draw a ray RY making an angle of 90° and cut off RS = 2.7 cm.
(iv) Join SP PQRS is the required quadrilateral.

Question 11.
Solution:
Steps of Construction :
∠A = 50°, ∠B = 105° and ∠D = 80°
and ∠A + ∠B + ∠C + ∠D = 360°
=> 50° + 105° + ∠C + 80° = 360°
=> ∠C + 235° = 360°
=> ∠C = 360° – 235°
=> ∠C = 125°

(i) Draw a line segment AB = 5.6 cm.
(ii) At B, draw a ray BY making an angle of 105° and cut off BC = 4 cm.
(iii) At C, draw a ray CZ making an. angle of 125° and at A, a ray AX making an angle of 50° intersecting each other at D.
then ∠D = 80°
ABCD is the required quadrilateral.

Question 12.
Solution:
∠P + ∠Q + ∠R + ∠S = 360°
100° + ∠Q + 100° + 75° = 360°
=> ∠Q + 275° = 360°
=> ∠Q = 360° – 275°
∠Q = 85°
Steps of Construction :

(i) Draw a line segment PQ = 5 cm.
(it) At Q, draw a ray QX making an angle of 85° and cut off QR = 6.5 cm.
(iii) At R, draw a ray making an angle of 100° and at P, another ray making an angle of 100° which intersect each other at S. then ∠S = 75°
PQRS is the required quadrilateral.

Question 13.
Solution:
Steps of Construction :

(i) Draw a line segment AB = 4 cm.
(ii) At B, draw a ray BX making an angle of 90°.
(iii) From A, draw an arc of 5 cm. radius intersecting BX at C.
(iv) Join AC.
(v) At C, draw a ray CY making an angle of 90°.
(vi) From A, draw an arc of radius 5.5 cm. which intersects CY at D.
(vii) Join AD.
ABCD is the required quadrilateral.

 

Hope given RS Aggarwal Solutions Class 8 Chapter 17 Construction of Quadrilaterals Ex 17A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.