Tag: ML Aggarwal Maths for Class 10 ICSE Solutions Pdf Download

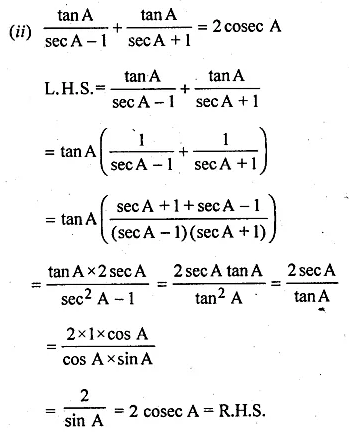
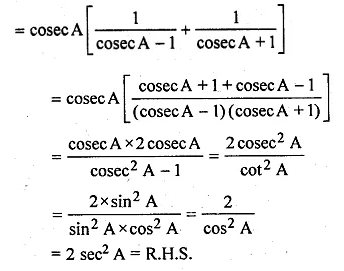
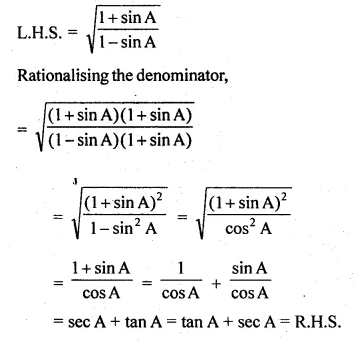
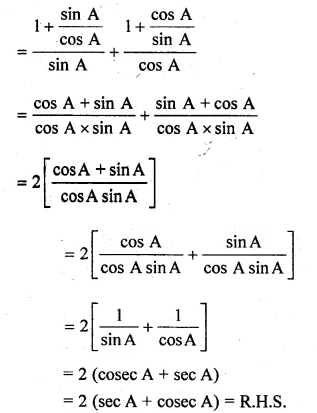
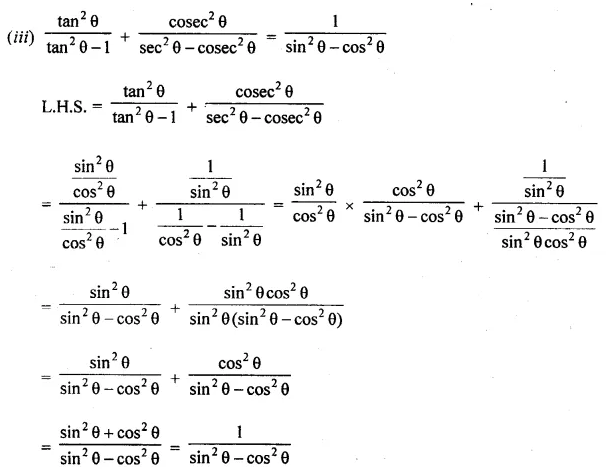
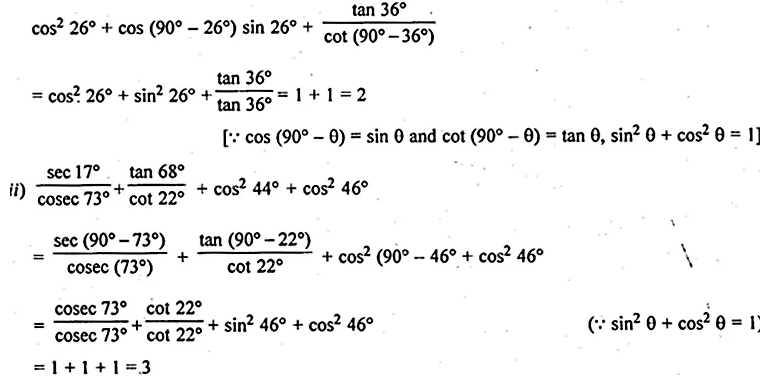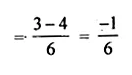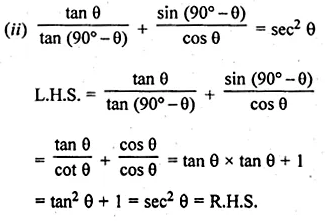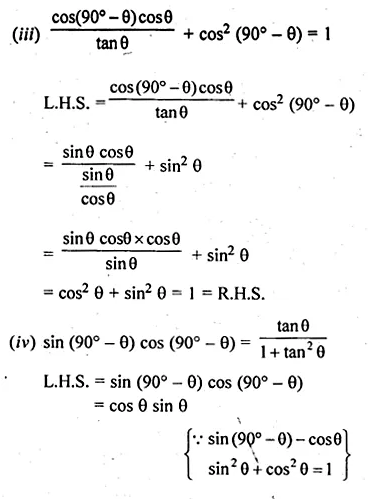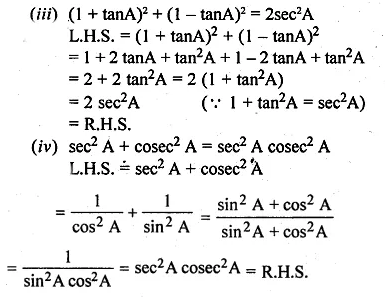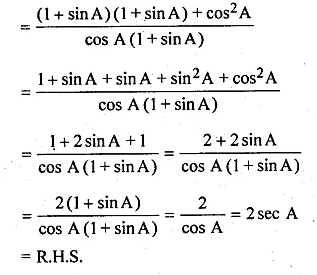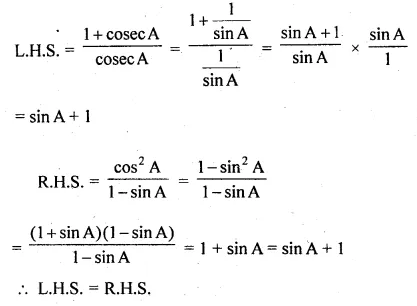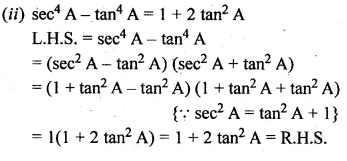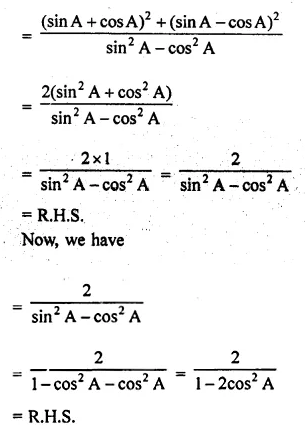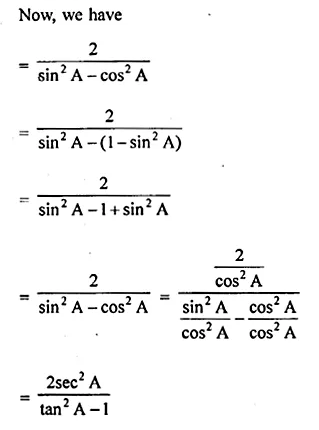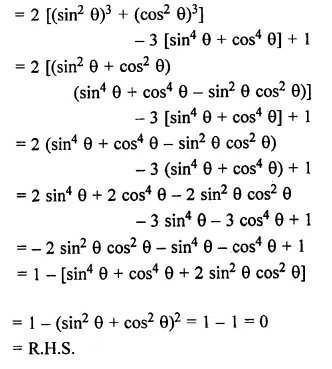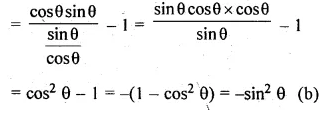ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Ex 22

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Ex 22

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Ex 22
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Chapter Test

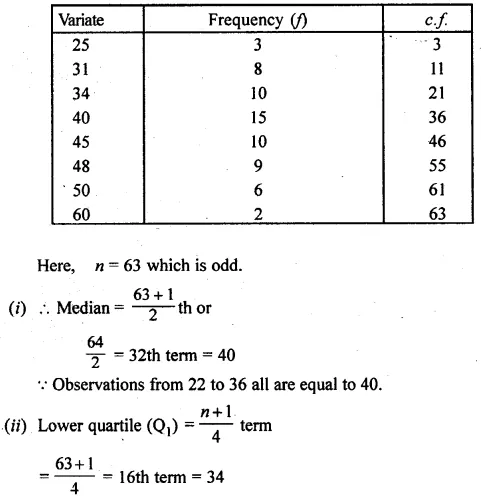
Question 1.
A bag contains a red ball, a blue ball and a yellow ball, all the balls being of the same size. Anjali takes out a ball from the bag without looking into it. What is the probability that she takes out
(i) yellow ball ?
(ii) red ball ?
(iii) blue ball ?
Solution:
Number of balls in the bag = 3.
(i) Probability of yellow ball = \(\\ \frac { 1 }{ 3 } \)
(ii) Probability of red ball = \(\\ \frac { 1 }{ 3 } \)
(iii) Probability of blue ball = \(\\ \frac { 1 }{ 3 } \)

Question 2.
A box contains 600 screws, one-tenth are rusted. One screw is taken out at random from this box. Find the probability that it is a good screw.
Solution:
Number of total screws = 600
Rusted screws = \(\\ \frac { 1 }{ 10 } \) of 600 = 60
∴ Good screws = 600 – 60 = 540
Probability of a good screw
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 540 }{ 600 } \)
= \(\\ \frac { 9 }{ 10 } \)

Question 3.
In a lottery, there are 5 prized tickets and 995 blank tickets. A person buys a lottery ticket. Find the probability of his winning a prize.
Solution:
Number of prized tickets = 5
Number of blank tickets = 995
Total number of tickets = 5 + 995 = 1000
Probability of prized ticket
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 5 }{ 1000 } \)
= \(\\ \frac { 1 }{ 200 } \)

Question 4.
12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is a good one.
Solution:
Number of defective pens = 12
Number of good pens = 132
Total number of pens =12 + 132 = 144
Probability of good pen
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 132 }{ 144 } \)
= \(\\ \frac { 11 }{ 12 } \)

Question 5.
If the probability of winning a game is \(\\ \frac { 5 }{ 11 } \), what is the probability of losing ?
Solution:
Probability of winning game = \(\\ \frac { 5 }{ 11 } \)
⇒ P(E) = \(\\ \frac { 5 }{ 11 } \)
We know that P (E) + P (\(\overline { E } \)) = 1
where P (E) is the probability of losing the game.
\(\\ \frac { 5 }{ 11 } \) + P (\(\overline { E } \)) = 1
⇒ P (\(\overline { E } \)) = \(1- \frac { 5 }{ 11 } \)
= \(\\ \frac { 11-5 }{ 11 } \)
= \(\\ \frac { 6 }{ 11 } \)

Question 6.
Two players, Sania and Sonali play a tennis match. It is known that the probability of Sania winning the match is 0.69. What is the probability of Sonali winning ?
Solution:
Probability of Sania’s winning the game = 0.69
Let P (E) be the probability of Sania’s winning the game
and P (\(\overline { E } \)) be the probability of Sania’s losing
the game or probability of Sonali, winning the game
P (E) + P (\(\overline { E } \)) = 1
⇒ 0.69 + P (\(\overline { E } \)) = 1
⇒ P(\(\overline { E } \)) = 1 – 0.69 = 0.31
Hence probability of Sonali’s winning the game = 0.31

Question 7.
A bag contains 3 red balls and 5 black balls. A ball is drawn at random’ from in bag. What is the probability that the ball drawn is .
(i) red ?
(ii) not red ?
Solution:
Number of red balls = 3
Number of black balls = 5
Total balls = 3 + 5 = 8
Let P (E) be the probability of red balls,
then P (\(\overline { E } \)) will be the probability of not red balls.
P (E) + P (\(\overline { E } \)) = 1
(i) But P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 3 }{ 8 } \)
(ii) P (\(\overline { E } \)) = 1 – P(E)
= \(1- \frac { 6 }{ 11 } \)
= \(\\ \frac { 8-3 }{ 8 } \)
= \(\\ \frac { 5 }{ 8 } \)

Question 8.
There are 40 students in Class X of a school of which 25 are girls and the.others are boys. The class teacher has to select one student as a class representative. She writes the name of each student on a separate card, the cards being identical. Then she puts cards in a bag and stirs them thoroughly. She then draws one card from the bag. What is the probability that the name written on the card is the name of
(i) a girl ?
(ii) a boy ?
Solution:
Number of total students = 40
Number of girls = 25
Number of boys = 40 – 25 = 15
(i) Probability of a girl
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 25 }{ 40 } \)
= \(\\ \frac { 5 }{ 8 } \)
(ii) Probability of a boy
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 15 }{ 40 } \)
= \(\\ \frac { 3 }{ 8 } \)

Question 9.
A letter is chosen from the word ‘TRIANGLE’. What is the probability that it is a vowel ?
Solution:
There are three vowels: I, A, E
.’. The number of letters in the word ‘TRIANGLE’ = 8.
Probability of vowel
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 3 }{ 8 } \)

Question 10.
A letter of English alphabet is chosen at random. Determine the probability that the letter is a consonant.
Solution:
No. of English alphabet = 26
No. of vowel = 5
No. of constant = 25 – 5 = 21
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 21 }{ 26 } \)

Question 11.
A bag contains 5 black, 7 red and 3 white balls. A ball is drawn at random from the bag, find the probability that the ball drawn is:
(i) red
(ii) black or white
(iii) not black.
Solution:
In a bag,
Number of black balls = 5
Number of red balls = 7
and number of white balls = 3
Total number of balls in the bag
= 5 + 7 + 3 = 15
(i) Probability of red balls
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 7 }{ 15 } \)
(ii) Probability of black or white balls
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 5+3 }{ 15 } \)
= \(\\ \frac { 8 }{ 15 } \)
(iii) Probability of not black balls
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 7+3 }{ 15 } \)
= \(\\ \frac { 10 }{ 15 } \)
= \(\\ \frac { 2 }{ 3 } \)

Question 12.
A box contains 7 blue, 8 white and 5 black marbles. If a marble is drawn at random from the box, what is the probability that it will be
(i) black?
(ii) blue or black?
(iii) not black?
(iv) green?
Solution:
Total number of marbles in the box
= 7 + 8 + 5 = 20
Since, a marble is drawn at random from the box
(i) Probability (of a black Marble)
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 5 }{ 20 } \)
= \(\\ \frac { 1 }{ 4 } \)
(ii) Probability (of a blue or black marble)
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 7+5 }{ 20 } \)
= \(\\ \frac { 12 }{ 20 } \)
= \(\\ \frac { 3 }{ 5 } \)
(iii) Probability (of not black marble)
= 1 – P (of black 1)
= \(1- \frac { 1 }{ 4 } \)
= \(\\ \frac { 4-1 }{ 4 } \)
= \(\\ \frac { 3 }{ 4 } \)
(iv) P (of a green marble) = 0
(∴ Since, a box does not contain a green marble,
so the probability of green marble will be zero)

Question 13.
A bag contains 6 red balls, 8 white balls, 5 green balls and 3 black balls. One ball is drawn at random from the bag. Find the probability that the ball is :
(i) white
(ii) red or black
(iii) not green
(iv) neither white nor black.
Solution:
In a bag,
Number of red balls = 6
Number of white balls = 8
Number of green balls = 5
and number of black balls = 3
Total number of balls in the bag
= 6 + 8 + 5 + 3 = 22
(i) Probability of white balls
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 8 }{ 22 } \)
= \(\\ \frac { 4 }{ 11 } \)
(ii) Probability of red or black balls
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6+3 }{ 22 } \)
= \(\\ \frac { 9 }{ 22 } \)
(iii) Probability of not green balls i.e. having red, white and black balls.
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6+8+3 }{ 22 } \)
= \(\\ \frac { 17 }{ 22 } \)
(iv) Probability of neither white nor black balls i.e. red and green balls
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6+5 }{ 22 } \)
= \(\\ \frac { 11 }{ 22 } \)
= \(\\ \frac { 1 }{ 2 } \)

Question 14.
A piggy bank contains hundred 50 p coins, fifty Rs 1 coins, twenty Rs 2 coins and ten Rs 5 coins. It is equally likely that one of the coins will fall down when the bank is turned upside down, what is the probability that the coin
(i) will be a 50 p coin?
(ii) will not be Rs 5 coin?
Solution:
In a piggy bank, there are
100, 50 p coin
50, Rs 1 coin
20, Rs 2 coin
10, Rs 5 coin
Total coins = 100 + 50 + 20 + 10 = 180
One coin is drawn at random Probability of
(i) 50 p coins = \(\\ \frac { 100 }{ 180 } \)
= \(\\ \frac { 5 }{ 9 } \)
(ii) Will not be Rs 5 coins
= 100 + 50 + 20 = 170
Probability = \(\\ \frac { 170 }{ 180 } \) = \(\\ \frac { 17 }{ 18 } \)

Question 15.
A carton consists of 100 shirts of which 88 are good, 8 have minor defects and 4 have major defects. Peter, a trader, will only accept the shirts which are good, but Salim, another trader, will only reject the shirts which have major defects. One shirts is drawn at random from the carton. What is the probability that
(i) it is acceptable to Peter ?
(ii) it is acceptable to Salim ?
Solution:
In a carton, there the 100 shirts.
Among these number of shirts which are good = 88
number of shirts which have minor defect = 8
number of shirt which have major defect = 4
Total number of shirts = 88 + 8 + 4 = 100
Peter accepts only good shirts i.e. 88
Salim rejects only shirts which have major defect i.e. 4
(i) Probability of good shirts which are acceptable to Peter
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 88 }{ 100 } \)
= \(\\ \frac { 22 }{ 25 } \)
(ii) Probability of shirts acceptable to Salim
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 88+8 }{ 100 } \)
= \(\\ \frac { 96 }{ 100 } \)
= \(\\ \frac { 24 }{ 25 } \)

Question 16.
A die is thrown once. What is the probability that the
(i) number is even
(ii) number is greater than 2 ?
Solution:
Dice is thrown once
Sample space = {1, 2, 3, 4, 5, 6}
(i) No. of ways in favour = 3
(∵ Even numbers are 2, 4, 6)
Total ways = 6
Probability = \(\\ \frac { 3 }{ 6 } \) = \(\\ \frac { 1 }{ 2 } \)
(ii) No. of ways in favour = 4
(Numbers greater than 2 are 3, 4, 5, 6)
Total ways = 6
Probability = \(\\ \frac { 4 }{ 6 } \) = \(\\ \frac { 2 }{ 2 } \)

Question 17.
In a single throw of a die, find the probability of getting:
(i) an odd number
(ii) a number less than 5
(iii) a number greater than 5
(iv) a prime number
(v) a number less than 8
(vi) a number divisible by 3
(vii) a number between 3 and 6
(viii) a number divisible by 2 or 3.
Solution:
A die is thrown and on its faces, numbers 1 to 6 are written.
Total numbers of possible outcomes = 6
(i) Probability of an odd number,
odd number are 1, 3 and 5
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 3 }{ 6 } \)
= \(\\ \frac { 1 }{ 2 } \)
(ii) A number less them 5 are 1, 2, 3, 4
Probability of a number less than 5 is
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 4 }{ 6 } \)
= \(\\ \frac { 2 }{ 3 } \)
(iii) A number greater than 5 is 6
Probability of a number greater than 5 is
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 1 }{ 6 } \)
(iv) Prime number is 2, 3, 5
Probability of a prime number is
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 3 }{ 6 } \)
= \(\\ \frac { 1 }{ 2 } \)
(v) Number less than 8 is nil
P (E) = 0
(vi) A number divisible by 3 is 3, 6
Probability of a number divisible by 3 is
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 2 }{ 6 } \)
= \(\\ \frac { 1 }{ 3 } \)
(vii) Numbers between 3 and 6 is 4, 5
Probability of a number between 3 and 6 is
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 2 }{ 6 } \)
= \(\\ \frac { 1 }{ 3 } \)
(viii) Numbers divisible by 2 or 3 are 2, 4 or 3,
Probability of a number between 2 or 3 is
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 2 }{ 6 } \)
= \(\\ \frac { 1 }{ 3 } \)

Question 18.
A die has 6 faces marked by the given numbers as shown below:

The die is thrown once. What is the probability of getting
(i) a positive integer.
(ii) an integer greater than – 3.
(iii) the smallest integer ?
Solution:
Total outcomes n(S)= 6
(i) a positive integer = (1, 2, 3)
No. of favourables n(E) = 3
Probability = \(\\ \frac { n(E) }{ n(S) } \)
= \(\\ \frac { 3 }{ 6 } \)
= \(\\ \frac { 1 }{ 2 } \)
(ii) Integer greater than -3
= (1, 2, 3, -1, -2)
No. of favourables n(E) = 5
Probability = \(\\ \frac { n(E) }{ n(S) } \)
= \(\\ \frac { 5 }{ 6 } \)
(iii) Smallest integer = -3
No. of favourables n(E) = 1
Probability = \(\\ \frac { n(E) }{ n(S) } \)
= \(\\ \frac { 1 }{ 6 } \)

Question 19.
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (shown in the adjoining figure) and these are equally likely outcomes. What is the probability that it will point at
(i) 8 ?
(ii) an odd number ?
(iii) a number greater than 2?
(iv) a number less than 9?

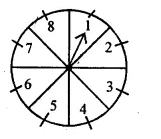
Solution:
On the face of a game, numbers 1 to 8 is shown.
Possible outcomes = 8
(i) Probability of number 8 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 1 }{ 8 } \)
(ii) Odd number are 1, 3, 5, 7
Probability of a number which is an odd will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 4 }{ 8 } \)
= \(\\ \frac { 1 }{ 2 } \)
(iii) A number greater than 2 are 3, 4, 5, 6, 7, 8 which are 6
Probability of number greater than 2 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6 }{ 8 } \)
= \(\\ \frac { 3 }{ 4 } \)
(iv) A number less than 9 is 8.
Probability of a number less than 9 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 8 }{ 8 } \)

Question 20.
Find the probability that the month of January may have 5 Mondays in
(i) a leap year
(ii) a non-leap year.
Solution:
In January, there are 31 days and in an ordinary year,
there are 365 days but in a leap year, there are 366 days.
(i) In January of an ordinary year, there are 31 days i.e. 4 weeks and 3 days.
Probability of Monday will be = \(\\ \frac { 3 }{ 7 } \)
(ii) In January of a leap year, there are 31 days i.e. 4 weeks and 3 days
Probability of Monday will be = \(\\ \frac { 3 }{ 7 } \)

Question 21.
Find the probability that the month of February may have 5 Wednesdays in
(i) a leap year
(ii) a non-leap year.
Solution:
In the month of February, there are 29 days in a leap year
while 28 days in a non-leap year,
(i) In a leap year, there are 4 complete weeks and 1 day
Probability of Wednesday = P (E) = \(\\ \frac { 1 }{ 7 } \)
(ii) and in a non leap year, there are 4 complete weeks and 0 days
Probability of Wednesday P (E) = \(\\ \frac { 0 }{ 7 } \) = 0

Question 22.
Sixteen cards are labelled as a, b, c,…, m, n, o, p. They are put in a box and shuffled. A boy is asked to draw a card from the box. What is the probability that the card drawn is:
(i) a vowel
(ii) a consonant
(iii) none of the letters of the word median.
Solution:
Here, sample space (S) = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p)
∴n(S) = 16
(i) Vowels (V) = {a, e, i, o}
∴n(V) = 4
∴P(a vowel) = \(\\ \frac { n(V) }{ n(S) } \) = \(\\ \frac { 4 }{ 16 } \) = \(\\ \frac { 1 }{ 4 } \)
(ii) Consonants (C) = {b, c, d, f, g, h, j, k, l, m, n, p}
∴n(C) = 12
∴P (a consonant) = \(\\ \frac { n(C) }{ n(S) } \) = \(\\ \frac { 12 }{ 16 } \) = \(\\ \frac { 3 }{ 4 } \)
(iii) None of the letters of the word MEDIAN (N) = {b, c, f, g, h, j, k, l, o, p)
∴n(N) = 10
∴P (N) = \(\\ \frac { n(N) }{ n(S) } \) = \(\\ \frac { 10 }{ 16 } \) = \(\\ \frac { 5 }{ 8 } \)

Question 23.
An integer is chosen between 0 and 100. What is the probability that it is
(i) divisible by 7?
(ii) not divisible by 7?
Solution:
Integers between 0 and 100 = 99
(i) Number divisible by 7 are
7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98 = 14
Probability = \(\\ \frac { 14 }{ 99 } \)
(ii) Not divisible by 7 are 99 – 14 = 85
Probability = \(\\ \frac { 85 }{ 99 } \)

Question 24.
Cards marked with numbers 1, 2, 3, 4, 20 are well shuffled and a card is drawn at random.
What is the probability that the number on the card is
(i) a prime number
(ii) divisible by 3
(iii) a perfect square ? (2010)
Solution:
Number cards is drawn from 1 to 20 = 20
One card is drawn at random
No. of total (possible) events = 20
(i) The card has a prime number
The prime number from 1 to 20 are 2, 3, 5, 7, 11, 13, 17, 19
Actual No. of events = 8
P(E) = \(\frac { Number\quad of\quad actual\quad events }{ Number\quad of\quad total\quad events } \)
= \(\\ \frac { 8 }{ 20 } \)
= \(\\ \frac { 2 }{ 5 } \)
(ii) Numbers divisible by 3 are 3, 6, 9, 12, 15, 18
No. of actual events = 6
P(E) = \(\frac { Number\quad of\quad actual\quad events }{ Number\quad of\quad total\quad events } \)
= \(\\ \frac { 6 }{ 20 } \)
= \(\\ \frac { 3 }{ 10 } \)
(iii) Numbers which are perfect squares = 1, 4, 9, 16 = 4
P(E) = \(\frac { Number\quad of\quad actual\quad events }{ Number\quad of\quad total\quad events } \)
= \(\\ \frac { 4 }{ 20 } \)
= \(\\ \frac { 1 }{ 5 } \)

Question 25.
A box contains 25 cards numbered 1 to 25. A card is drawn from the box at random. Find the probability that the number on the card is :
(i) even
(ii) prime
(iii) multiple of 6
Solution:
Number of card in a box = 25 numbered 1 to 25
(i) Even numbers are 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24
i.e. number of favourable outcomes = 12
Probability of an even number will be
P(E) = \(\\ \frac { 12 }{ 25 } \)
(ii) Prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23
i.e. number of primes = 9
Probability of primes will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 9 }{ 25 } \)
(iii) Multiples of 6 are 6, 12, 18, 24
Number of multiples = 4
Probability of multiples of 6 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 4 }{ 25 } \)

Question 26.
A box contains 15 cards numbered 1, 2, 3,…..15 which are mixed thoroughly. A card is drawn from the box at random. Find the probability that the number on the card is :
(i) Odd
(ii) prime
(iii) divisible by 3
(iv) divisible by 3 and 2 both
(v) divisible by 3 or 2
(vi) a perfect square number.
Solution:
Number of cards in a box =15 numbered 1 to 15
(i) Odd numbers are 1, 3, 5, 7, 9, 11, 13, 15
Number of odd numbers = 8
Probability of odd numbers will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 8 }{ 15 } \)
(ii) Prime number are 2, 3, 5, 7, 11, 13
Number of primes is 6
Probability of prime number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6 }{ 15 } \)
= \(\\ \frac { 2 }{ 5 } \)
(iii) Numbers divisible by 3 are 3, 6, 9, 12, 15
which are 5 in numbers
Probability of number divisible by 3 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 5 }{ 15 } \)
= \(\\ \frac { 1 }{ 3 } \)
(iv) Divisible by 3 and 2 both are 6, 12
which are 2 in numbers.
Probability of number divisible by 3 and 2
Both will be = \(\\ \frac { 2 }{ 15 } \)
(v) Numbers divisible by 3 or 2 are
2, 3, 4, 6, 8, 9, 10, 12, 14, 15 which are 10 in numbers
Probability of number divisible by 3 or 2 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 10 }{ 15 } \)
= \(\\ \frac { 2 }{ 3 } \)
(v) Perfect squares number are 1, 4, 9 i.e., 3 number
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 3 }{ 15 } \)
= \(\\ \frac { 1 }{ 5 } \)

Question 27.
A box contains 19 balls bearing numbers 1, 2, 3,…., 19. A ball is drawn at random
from the box. Find the probability that the number on the ball is :
(i) a prime number
(ii) divisible by 3 or 5
(iii) neither divisible by 5 nor by 10
(iv) an even number.
Solution:
In a box, number of balls = 19 with number 1 to 19.
A ball is drawn
Number of possible outcomes = 19
(i) Prime number = 2, 3, 5, 7, 11, 13, 17, 19
which are 8 in number
Probability of prime number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 8 }{ 19 } \)
(ii) Divisible by 3 or 5 are 3, 5, 6, 9, 10, 12, 15, 18
which are 8 in number
Probability of number divisible by 3 or 5 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 8 }{ 19 } \)
(iii) Numbers which are neither divisible by 5 nor by 10 are
1, 2, 3, 4, 6, 7, 8, 9, 11, 12,
13, 14, 16, 17, 18, 19
which are 16 in numbers
Probability of there number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 16 }{ 19 } \)
(iv) Even numbers are 2, 4, 6, 8, 10, 12, 14, 16, 18
which are 9 in numbers.
Probability of there number will be
Number of favourable outcome
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 9 }{ 19 } \)

Question 28.
Cards marked with numbers 13, 14, 15, …, 60 are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that the number on the card drawn is
(i) divisible by 5
(ii) a perfect square number.
Solution:
Number of card bearing numbers 13,14,15, … 60 = 48
One card is drawn at random.
(i) Card divisible by 5 are 15, 20, 25, 30, 35, 40, 45, 50, 55, 60 = 10
Probability = \(\\ \frac { 10 }{ 48 } \)
= \(\\ \frac { 5 }{ 24 } \)
(ii) A perfect square = 16, 25, 36, 49 = 4
Probability = \(\\ \frac { 4 }{ 48 } \)
= \(\\ \frac { 1 }{ 12 } \)

Question 29.
Tickets numbered 3, 5, 7, 9,…., 29 are placed in a box and mixed thoroughly. One ticket is drawn at random from the box. Find the probability that the number on the ticket is
(i) a prime number
(ii) a number less than 16
(iii) a number divisible by 3.
Solution:
In a box there are 14 tickets with number
3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29
Number of possible outcomes = 14
(i) Prime numbers are 3, 5, 7, 11, 13, 17, 19, 23, 29
which are 9 in number
Probability of prime will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 9 }{ 14 } \)
(ii) Number less than 16 are 3, 5, 7, 9, 11, 13, 15
which are 7 in numbers,
Probability of number less than 16 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 7 }{ 14 } \)
= \(\\ \frac { 1 }{ 2 } \)
(iii) Numbers divisible by 3 are 3, 9, 15, 21, 27
which are 5 in number
Probability of number divisible by 3 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 5 }{ 14 } \)

Question 30.
A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears
(i) a two-digit number
(ii) a perfect square number
(iii) a number divisible by 5.
Solution:
There are 90 discs in a box containing numbered from 1 to 90.
Number of possible outcomes = 90
(i) Two digit numbers are 10 to 90 which are 81 in numbers.
Probability of two digit number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 81 }{ 90 } \)
= \(\\ \frac { 9 }{ 10 } \)
(ii) Perfect squares are 1, 4, 9, 16, 25, 36,49, 64, 81
which are 9 in numbers.
Probability of square will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 9 }{ 90 } \)
= \(\\ \frac { 1 }{ 10 } \)
(iii) Number divisible by 5 are
5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90
which are 18 in numbers.
Probability of number divisible by 5 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 18 }{ 90 } \)
= \(\\ \frac { 1 }{ 5 } \)

Question 31.
Cards marked with numbers 2 to 101 are placed in a box and mixed thoroughly. One card is drawn at random from this box. Find the probability that the number on the card is
(i) an even number
(ii) a number less than 14
(iii) a number which is a perfect square
(iv) a prime number less than 30.
Solution:
Number of cards with numbered from 2 to 101 are placed in a box
Number of possible outcomes = 100 one card is drawn
(i) Even numbers are 2, 4, 6, 8, 10, 12, 14, 16,….., 96, 98, 100
which are 50 in numbers.
Probability of even number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 50 }{ 100 } \)
= \(\\ \frac { 1 }{ 2 } \)
(ii) Numbers less than 14 are 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13
which are 12 in numbers
Probability of number less than 14 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 12 }{ 100 } \)
= \(\\ \frac { 3 }{ 25 } \)
(iii) Perfect square are 4, 9, 16, 25, 36, 49, 64, 81, 100 which are 9 in numbers
Probability of perfect square number will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 9 }{ 100 } \)
(iv) Prime numbers less than 30 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
which are 10 in numbers Probability of prime numbers, less than 30 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 10 }{ 100 } \)
= \(\\ \frac { 1 }{ 10 } \)

Question 32.
A bag contains 15 balls of which some are white and others are red. If the probability of drawing a red ball is twice that of a white ball, find the number of white balls in the bag.
Solution:
In a bag, there are 15 balls.
Some are white and others are red.
Probability of red ball = 2 probability of white ball
Let number of white balls = x
Then, number of red balls = 15 – x
\(2\times \frac { 15-x }{ 15 } =\frac { x }{ 15 } \)
⇒ 2(15 – x) = x
⇒ 30 – 2x = x
⇒ 30 = x + 2x
⇒ x = \(\\ \frac { 30 }{ 3 } \) = 10
Number of red balls = 10
and Number of white balls = 15 – 10 = 5

Question 33.
A bag contains 6 red balls and some blue balls. If the probability of drawing a blue ball is twice that of a red ball, find the number of balls in the bag.
Solution:
In a bag, there are 6 red balls, and some blue balls
Probability of blue ball = 2 × probability of red ball
Let number of blue balls = x
and number of red balls = 6
Total balls = x + 6
Probability of a blue ball = 2
⇒ \(\frac { x }{ x+6 } =2\times \frac { 6 }{ x+6 } \)
⇒ \(\frac { x }{ x+6 } =\frac { 12 }{ x+6 } \)
⇒ x = 12
Number of balls = x + 6 = 12 + 6 = 18

Question 34.
A bag contains 24 balls of which x are red, 2x are white and 3x are blue. A blue is selected at random. Find the probability that it is
(i) white
(ii) not red.
Solution:
In a bag, there are 24 balls
Since, there are x balls red, 2 × balls white and 3 × balls blue
x + 2x + 3x = 24

Question 35.
A card is drawn from a well-shuffled pack of 52 cards. Find the probability of getting:
(i) ‘2’ of spades
(ii) a jack .
(iii) a king of red colour
(iv) a card of diamond
(v) a king or a queen
(vi) a non-face card
(vii) a black face card
(viii) a black card
(ix) a non-ace
(x) non-face card of black colour
(xi) neither a spade nor a jack
(xii) neither a heart nor a red king
Solution:
In a playing card, there are 52 cards
Number of possible outcome = 52
(i) Probability of‘2’ of spade will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 1 }{ 52 } \)
(ii) There are 4 jack card Probability of jack will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 4 }{ 52 } \)
= \(\\ \frac { 1 }{ 13 } \)
(iii) King of red colour are 2 in number
Probability of red colour king will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 2 }{ 52 } \)
= \(\\ \frac { 1 }{ 26 } \)
(iv) Cards of diamonds are 13 in number
Probability of diamonds card will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 13 }{ 52 } \)
= \(\\ \frac { 1 }{ 4 } \)
(v) Number of kings and queens = 4 + 4 = 8
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 8 }{ 52 } \)
= \(\\ \frac { 2 }{ 13 } \)
(vi) Non-face cards are = 52 – 3 × 4 = 52 – 12 = 40
Probability of non-face card will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 40 }{ 52 } \)
= \(\\ \frac { 10 }{ 13 } \)
(vii) Black face cards are = 2 × 3 = 6
Probability of black face card will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6 }{ 52 } \)
= \(\\ \frac { 3 }{ 26 } \)
(viii) No. of black cards = 13 x 2 = 26
Probability of black card will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 26 }{ 52 } \)
= \(\\ \frac { 1 }{ 2 } \)
(ix) Non-ace cards are 12 × 4 = 48
Probability of non-ace card will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 48 }{ 52 } \)
= \(\\ \frac { 12 }{ 13 } \)
(x) Non-face card of black colours are 10 × 2 = 20
Probability of non-face card of black colour will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 20 }{ 52 } \)
= \(\\ \frac { 5 }{ 13 } \)
(xi) Number of card which are neither a spade nor a jack
= 13 × 3 – 3 = 39 – 3 = 36
Probability of card which is neither a spade nor a jack will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 36 }{ 52 } \)
= \(\\ \frac { 9 }{ 13 } \)
(xii) Number of cards which are neither a heart nor a red king
= 3 × 13 = 39 – 1 = 38
Probability of card which is neither a heart nor a red king will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 38 }{ 52 } \)
= \(\\ \frac { 19 }{ 26 } \)

Question 36.
All the three face cards of spades are removed from a well-shuffled pack of 52 cards. A card is then drawn at random from the remaining pack. Find the probability of getting
(i) a black face card
(ii) a queen
(iii) a black card
(iv) a heart
(v) a spade
(vi) ‘9’ of black colour
Solution:
In a pack of 52 cards
All the three face cards of spade are = 3
Number of remaining cards = 52 – 3 = 49
One card is drawn at random
(i) Probability of a black face card which are = 6 – 3 = 3
Probability = \(\\ \frac { 3 }{ 49 } \)
(ii) Probability of being a queen which are 4 – 1 = 3
Probability = \(\\ \frac { 3 }{ 49 } \)
(iii) Probability of being a black card = (26 – 3 = 23)
Probability = \(\\ \frac { 23 }{ 49 } \)
(iv) Probability of being a heart = \(\\ \frac { 13 }{ 49 } \)
(v) Probability of being a spade = (13 – 3 = 10)
Probability = \(\\ \frac { 10 }{ 49 } \)
(vi) Probability of being 9 of black colour (which are 2) = \(\\ \frac { 2 }{ 49 } \)

Question 37.
From a pack of 52 cards, a blackjack, a red queen and two black kings fell down. A card was then drawn from the remaining pack at random. Find the probability that the card drawn is
(i) a black card
(ii) a king
(iii) a red queen.
Solution:
In a pack of 52 cards, a blackjack, a red queen, two black being felt down.
Then number of total out comes = 52 – (1 + 1 + 2) = 48
(i) Probability of a black card (which are 26 – 3 = 23) = \(\\ \frac { 23 }{ 48 } \)
(ii) Probability of a being (4 – 2 = 2) = \(\\ \frac { 2 }{ 48 } \) = \(\\ \frac { 1 }{ 24 } \)
(iii) Probability of a red queen = (2 – 1 = 1) = \(\\ \frac { 1 }{ 48 } \)

Question 38.
Two coins are tossed once. Find the probability of getting:
(i) 2 heads
(ii) at least one tail.
Solution:
Total possible outcomes are . HH, HT, TT, TH, i.e., 4
(i) Favourable outcomes are HH, i.e., 1
So, P(2 heads)
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 1 }{ 4 } \)
(ii) Favourable outcomes are HT, TT, TH, i.e., 3
So, P (at least one tail) = \(\\ \frac { 3 }{ 4 } \)

Question 39.
Two different coins are tossed simultaneously. Find the probability of getting :
(i) two tails
(ii) one tail
(iii) no tail
(iv) atmost one tail.
Solution:
Two different coins are tossed simultaneously
Number of possible outcomes = (2)² = 4
Number of event having two tails = 1 i.e. (T, T)
(i) Probability of two tails will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 1 }{ 4 } \)
(ii) Number of events having one tail = 2 i.e. (TH) and (HT)
Probability of one tail will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 1 }{ 4 } \)
(iii) Number of events having no tail = 1 i.e. (HH)
Probability of having no tail will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 1 }{ 4 } \)
(iv) Atmost one tail
Number Of events having at the most one tail = 3 i.e. (TH), (HT, (TT)
Probability of at the most one tail will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 3 }{ 4 } \)

Question 40.
Two different dice are thrown simultaneously. Find the probability of getting:
(i) a number greater than 3 on each dice
(ii) an odd number on both dice.
Solution:
When two different dice are thrown simultaneously,
then the sample space S of the random experiment =
{(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6) .
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)}
It consists of 36 equally likely outcomes.
(i) Let E be the event of ‘a number greater than 3 on each dice’.
E = {(4, 4), (4, 5), (4, 6), (5, 4), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)}
No. of favourable outcomes (E) = 9
P (number greater than 3 on each dice) = \(\\ \frac { 9 }{ 36 } \) = \(\\ \frac { 1 }{ 4 } \)
(ii) Let E be the event of ‘an odd number on both dice’.
E = {(1, 1), (1, 3), (1, 5), (3, 1), (3, 3), (3, 5), (5, 1), (5, 3), (5, 5)}
No. of favourable outcomes (E) = 9
∴ P (Odd on both dices) = \(\\ \frac { 9 }{ 36 } \) = \(\\ \frac { 1 }{ 4 } \)

Question 41.
Two different dice are thrown at the same time. Find the probability of getting :
(i) a doublet
(ii) a sum of 8
(iii) sum divisble by 5
(iv) sum of atleast 11.
Solution:
Two different dice are thrown at the same time
Possible outcomes will be (6)² i.e. 36
(i) Number of events which doublet = 6
i.e. (1, 1), (2, 2) (3, 3), (4, 4), (5, 5) and (6, 6)
.’. Probability of doublets will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 6 }{ 36 } \)
= \(\\ \frac { 1 }{ 6 } \)
(ii) Number of event in which the sum is 8 are
(2, 6), (3, 5), (4, 4), (5, 3), (6, 2) = 5
Probability of a sum of 8 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 5 }{ 36 } \)
(iii) Number of event when sum is divisible by
5 are (1, 4), (4, 1), (2, 3), (3, 2), (4, 6),
(5, 5) = 7 in numbers
Probability of sum divisible by 5 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 7 }{ 36 } \)
(iv) Sum of atleast 11, will be in following events
(5, 6), (6, 5), (6, 6)
Probability of sum of atleast 11 will be
P(E) = \(\frac { Number\quad of\quad favourable\quad outcome }{ Number\quad of\quad possible\quad outcome } \)
= \(\\ \frac { 3 }{ 36 } \)
= \(\\ \frac { 1 }{ 12 } \)

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Ex 22 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 22 Probability Ex 22, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test

Question 1.
If A is an acute angle and sin A = \(\\ \frac { 3 }{ 5 } \) find all other trigonometric ratios of angle A (using trigonometric identities).
Solution:
sin A = \(\\ \frac { 3 }{ 5 } \)
In ∆ABC, ∠B = 90°
AC = 5 and BC = 3

Question 2.
If A is an acute angle and sec A = \(\\ \frac { 17 }{ 8 } \), find all other trigonometric ratios of angle A (using trigonometric identities).
Solution:
sec A = \(\\ \frac { 17 }{ 8 } \) (A is an acute angle)
In right ∆ABC
sec A = \(\\ \frac { AC }{ AB } \) = \(\\ \frac { 17 }{ 8 } \)
AC = 17, AB = 8

Question 3.
Express the ratios cos A, tan A and sec A in terms of sin A.
Solution:
cos A = \(\sqrt { { 1-sin }^{ 2 }A } \)
tan A = \(\frac { SinA }{ CosA } =\frac { sinA }{ \sqrt { { 1-sin }^{ 2 }A } } \)
sec A = \(\frac { 1 }{ cosA } =\frac { 1 }{ \sqrt { { 1-sin }^{ 2 }A } } \)

Question 4.
If tan A = \(\frac { 1 }{ \sqrt { 3 } } \), find all other trigonometric ratios of angle A.
Solution:
tan A = \(\frac { 1 }{ \sqrt { 3 } } \)
In right ∆ABC,
tan A = \(\\ \frac { BC }{ AB } \) = \(\frac { 1 }{ \sqrt { 3 } } \)

Question 5.
If 12 cosec θ = 13, find the value of \(\frac { 2sin\theta -3cos\theta }{ 4sin\theta -9cos\theta } \)
Solution:
12 cosec θ = 13
⇒ cosec θ = \(\\ \frac { 13 }{ 12 } \)
In right ∆ABC,
∠A = θ
cosec θ = \(\\ \frac { AC }{ BC } \) = \(\\ \frac { 13 }{ 12 } \)

Without using trigonometric tables, evaluate the following (6 to 10) :

Question 6.
(i) cos² 26° + cos 64° sin 26° + \(\frac { tan{ 36 }^{ O } }{ { cot54 }^{ O } } \)
(ii) \(\frac { sec{ 17 }^{ O } }{ { cosec73 }^{ O } } +\frac { tan68^{ O } }{ cot22^{ O } } \) + cos² 44° + cos² 46°
Solution:
Given that
(i) cos² 26° + cos 64° sin 26° + \(\frac { tan{ 36 }^{ O } }{ { cot54 }^{ O } } \)

Question 7.
(i) \(\frac { sin65^{ O } }{ { cos25 }^{ O } } +\frac { cos32^{ O } }{ sin58^{ O } } \) – sin 28° sec 62° + cosec² 30° (2015)
(ii) \(\frac { sin29^{ O } }{ { cosec61 }^{ O } } \) + 2 cot 8° cot 17° cot 45° cot 73° cot 82° – 3(sin² 38° + sin² 52°).
Solution:
given that
(i) \(\frac { sin65^{ O } }{ { cos25 }^{ O } } +\frac { cos32^{ O } }{ sin58^{ O } } \) – sin 28° sec 62° + cosec² 30°

Question 8.
(i) \(\frac { { sin }35^{ O }{ cos55 }^{ O }+{ cos35 }^{ O }{ sin }55^{ O } }{ { cosec }^{ 2 }{ 10 }^{ O }-{ tan }^{ 2 }{ 80 }^{ O } } \)
(ii) \({ sin }^{ 2 }{ 34 }^{ O }+{ sin }^{ 2 }{ 56 }^{ O }+2tan{ 18 }^{ O }{ tan72 }^{ O }-{ cot }^{ 2 }{ 30 }^{ O }\)
Solution:
Given that
(i) \(\frac { { sin }35^{ O }{ cos55 }^{ O }+{ cos35 }^{ O }{ sin }55^{ O } }{ { cosec }^{ 2 }{ 10 }^{ O }-{ tan }^{ 2 }{ 80 }^{ O } } \)

Question 9.
(i) \({ \left( \frac { { tan25 }^{ O } }{ { cosec }65^{ O } } \right) }^{ 2 }+{ \left( \frac { { cot25 }^{ O } }{ { sec65 }^{ O } } \right) }^{ 2 }+{ 2tan18 }^{ O }{ tan }45^{ O }{ tan72 }^{ O } \)
(ii) \(\left( { cos }^{ 2 }25+{ cos }^{ 2 }65 \right) +cosec\theta sec\left( { 90 }^{ O }-\theta \right) -cot\theta tan\left( { 90 }^{ O }-\theta \right) \)
Solution:
(i) \({ \left( \frac { { tan25 }^{ O } }{ { cosec }65^{ O } } \right) }^{ 2 }+{ \left( \frac { { cot25 }^{ O } }{ { sec65 }^{ O } } \right) }^{ 2 }+{ 2tan18 }^{ O }{ tan }45^{ O }{ tan72 }^{ O } \)

Question 10.
(i) 2(sec² 35° – cot² 55°) – \(\frac { { cos28 }^{ O }cosec{ 62 }^{ O } }{ { tan18 }^{ O }tan{ 36 }^{ O }{ tan30 }^{ O }{ tan54 }^{ O }{ tan72 }^{ O } } \)
(ii) \(\frac { { cosec }^{ 2 }(90-\theta )-{ tan }^{ 2 }\theta }{ 2({ cos }^{ 2 }{ 48 }^{ O }+{ cos }^{ 2 }{ 42 }^{ O }) } -\frac { { 2tan }^{ 2 }{ 30 }^{ O }{ sec }^{ 2 }{ 52 }^{ O }{ sin }^{ 2 }{ 38 }^{ O } }{ { cosec }^{ 2 }{ 70 }^{ O }-{ tan }^{ 2 }{ 20 }^{ O } } \)
Solution:
(i) 2(sec² 35° – cot² 55°) – \(\frac { { cos28 }^{ O }cosec{ 62 }^{ O } }{ { tan18 }^{ O }tan{ 36 }^{ O }{ tan30 }^{ O }{ tan54 }^{ O }{ tan72 }^{ O } } \)

Question 11.
Prove that following:
(i) cos θ sin (90° – θ) + sin θ cos (90° – θ) = 1
(ii) \(\frac { tan\theta }{ tan({ 90 }^{ O }-\theta ) } +\frac { sin({ 90 }^{ O }-\theta ) }{ cos\theta } ={ sec }^{ 2 }\theta \)
(iii) \(\frac { cos({ 90 }^{ O }-\theta )cos\theta }{ tan\theta } +{ cos }^{ 2 }({ 90 }^{ O }-\theta )=1\)
(iv) sin (90° – θ) cos (90° – θ) = \(\frac { tan\theta }{ { 1+tan }^{ 2 }\theta } \)
Solution:
(i) cos θ sin (90° – θ) + sin θ cos (90° – θ) = 1
L.H.S. = cos θ sin (90° – θ) + sin θ cos (90° – θ)
= cos θ . cos θ + sin θ . sin θ
= cos² θ + sin² θ = 1 = R.H.S.

Prove that following (12 to 30) identities, where the angles involved are acute angles for which the trigonometric ratios as defined:

Question 12.
(i) (sec A + tan A) (1 – sin A) = cos A
(ii) (1 + tan² A) (1 – sin A) (1 + sin A) = 1.
Solution:
(i) (sec A + tan A) (1 – sin A) = cos A
L.H.S. = (sec A + tan A) (1 – sin A)

Question 13.
(i) tan A + cot A = sec A cosec A
(ii) (1 – cos A)(1 + sec A) = tan A sin A.
Solution:
(i) tan A + cot A = sec A cosec A
L.H.S. = tan A + cot A

Question 14.
(i) \(\frac { 1 }{ 1+cosA } +\frac { 1 }{ 1-cosA } =2{ cosec }^{ 2 }A\)
(ii) \(\frac { 1 }{ secA+tanA } +\frac { 1 }{ secA-tanA } =2{ sec }A\)
Solution:
(i) \(\frac { 1 }{ 1+cosA } +\frac { 1 }{ 1-cosA } =2{ cosec }^{ 2 }A\)
L.H.S = \(\frac { 1 }{ 1+cosA } +\frac { 1 }{ 1-cosA }\)

Question 15.
(i) \(\frac { sinA }{ 1+cosA } =\frac { 1-cosA }{ sinA } \)
(ii) \(\frac { 1-{ tan }^{ 2 }A }{ { cot }^{ 2 }A-1 } ={ tan }^{ 2 }A\)
(iii) \(\frac { sinA }{ 1+cosA } =cosecA-cotA\)
Solution:
(i) \(\frac { sinA }{ 1+cosA } =\frac { 1-cosA }{ sinA } \)
L.H.S = \(\frac { sinA }{ 1+cosA } \)
(multiplying and dividing by (1 – cosA))

Question 16.
(i) \(\frac { secA-1 }{ secA+1 } =\frac { 1-cosA }{ 1+cosA } \)
(ii) \(\frac { { tan }^{ 2 }\theta }{ { (sec\theta -1) }^{ 2 } } =\frac { 1+cos\theta }{ 1-cos\theta } \)
(iii) \({ (1+tanA) }^{ 2 }+{ (1-tanA) }^{ 2 }=2{ sec }^{ 2 }A\)
(iv) \({ sec }^{ 2 }A+{ cosec }^{ 2 }A={ sec }^{ 2 }A{ .cosec }^{ 2 }A\)
Solution:
(i) \(\frac { secA-1 }{ secA+1 } =\frac { 1-cosA }{ 1+cosA } \)
L.H.S = \(\frac { secA-1 }{ secA+1 } \)

Question 17.
(i) \(\frac { 1+sinA }{ cosA } +\frac { cosA }{ 1+sinA } =2secA \)
(ii) \(\frac { tanA }{ secA-1 } +\frac { tanA }{ secA+1 } =2cosecA\)
Solution:
(i) \(\frac { 1+sinA }{ cosA } +\frac { cosA }{ 1+sinA } =2secA \)
L.H.S = \(\frac { 1+sinA }{ cosA } +\frac { cosA }{ 1+sinA } \)

Question 18.
(i) \(\frac { cosecA }{ cosecA-1 } +\frac { cosecA }{ cosecA+1 } =2{ sec }^{ 2 }A\)
(ii) \(cotA-tanA=\frac { { 2cos }^{ 2 }A-1 }{ sinA-cosA } \)
(iii) \(\frac { cotA-1 }{ 2-{ sec }^{ 2 }A } =\frac { cotA }{ 1+tanA } \)
Solution:
(i) \(\frac { cosecA }{ cosecA-1 } +\frac { cosecA }{ cosecA+1 } =2{ sec }^{ 2 }A\)
L.H.S = \(\frac { cosecA }{ cosecA-1 } +\frac { cosecA }{ cosecA+1 } \)

Question 19.
(i) \({ tan }^{ 2 }\theta -{ sin }^{ 2 }\theta ={ tan }^{ 2 }\theta { sin }^{ 2 }\theta \)
(ii) \(\frac { cos\theta }{ 1-tan\theta } -\frac { { sin }^{ 2 }\theta }{ cos\theta -sin\theta } =cos\theta +sin\theta \)
Solution:
(i) \({ tan }^{ 2 }\theta -{ sin }^{ 2 }\theta ={ tan }^{ 2 }\theta { sin }^{ 2 }\theta \)
L.H.S = \({ tan }^{ 2 }\theta -{ sin }^{ 2 }\theta \)

Question 20.
(i) cosec⁴ θ – cosec² θ = cot⁴ θ + cot² θ
(ii) 2 sec² θ – sec⁴ θ – 2 cosec² θ + cosec⁴ θ = cot⁴ θ – tan⁴ θ.
Solution:
(i) cosec⁴ θ – cosec² θ = cot⁴ θ + cot² θ
L.H.S = cosec⁴ θ – cosec² θ

Question 21.
(i) \(\frac { 1+cos\theta -{ sin }^{ 2 }\theta }{ sin\theta (1+cos\theta ) } =cot\theta \)
(ii) \(\frac { { tan }^{ 3 }\theta -1 }{ tan\theta -1 } ={ sec }^{ 2 }\theta +tan\theta \)
Solution:
(i) \(\frac { 1+cos\theta -{ sin }^{ 2 }\theta }{ sin\theta (1+cos\theta ) } =cot\theta \)
L.H.S = \(\frac { 1+cos\theta -{ sin }^{ 2 }\theta }{ sin\theta (1+cos\theta ) }\)

Question 22.
(i) \(\frac { 1+cosecA }{ cosecA } =\frac { { cos }^{ 2 }A }{ 1-sinA } \)
(ii) \(\sqrt { \frac { 1-cosA }{ 1+cosA } } =\frac { sinA }{ 1+cosA } \)
Solution:
(i) \(\frac { 1+cosecA }{ cosecA } =\frac { { cos }^{ 2 }A }{ 1-sinA } \)
L.H.S = \(\frac { 1+cosecA }{ cosecA }\)

Question 23.
(i) \(\sqrt { \frac { 1+sinA }{ 1-sinA } } =tanA+secA\)
(ii) \(\sqrt { \frac { 1-cosA }{ 1+cosA } } =cosecA-cotA\)
Solution:
(i) \(\sqrt { \frac { 1+sinA }{ 1-sinA } } =tanA+secA\)
L.H.S = \(\sqrt { \frac { 1+sinA }{ 1-sinA } } \)

Question 24.
(i) \(\sqrt { \frac { secA-1 }{ secA+1 } } +\sqrt { \frac { secA+1 }{ secA-1 } } =2cosecA\)
(ii) \(\frac { cotAcotA }{ 1-sinA } =1+cosecA \)
Solution:
(i) \(\sqrt { \frac { secA-1 }{ secA+1 } } +\sqrt { \frac { secA+1 }{ secA-1 } } =2cosecA\)
L.H.S = \(\sqrt { \frac { secA-1 }{ secA+1 } } +\sqrt { \frac { secA+1 }{ secA-1 } } \)

Question 25.
(i) \(\frac { 1+tanA }{ sinA } +\frac { 1+cotA }{ cosA } =2(secA+cosecA)\)
(ii) \({ sec }^{ 4 }A-{ tan }^{ 4 }A=1+2{ tan }^{ 2 }A \)
Solution:
(i) \(\frac { 1+tanA }{ sinA } +\frac { 1+cotA }{ cosA } =2(secA+cosecA)\)
L.H.S = \(\frac { 1+tanA }{ sinA } +\frac { 1+cotA }{ cosA } \)

Question 26.
(i) cosec⁶ A – cot⁶ A = 3 cot² A cosec² A + 1
(ii) sec⁶ A – tan⁶ A = 1 + 3 tan² A + 3 tan⁴ A
Solution:
(i) cosec⁶ A – cot⁶ A = 3 cot² A cosec² A + 1
L.H.S = cosec⁶ A – cot⁶ A

Question 27.
(i) \(\frac { cot\theta -cosec\theta -1 }{ cot\theta -cosec\theta +1 } =\frac { 1+cos\theta }{ sin\theta } \)
(ii) \(\frac { sin\theta }{ cot\theta +cosec\theta } =2+\frac { sin\theta }{ cot\theta -cosec\theta } \)
Solution:
(i) \(\frac { cot\theta -cosec\theta -1 }{ cot\theta -cosec\theta +1 } =\frac { 1+cos\theta }{ sin\theta } \)
L.H.S = \(\frac { cot\theta -cosec\theta -1 }{ cot\theta -cosec\theta +1 }\)

Question 28.
(i) (sinθ + cosθ)(secθ + cosecθ) = 2 + secθ cosecθ
(ii) (cosecA – sinA)(secA – cosA) sec²A = tanA
(iii) (cosecθ – sinθ)(secθ – cosθ)(tan θ + cotθ) = 1
Solution:
(i) (sinθ + cosθ)(secθ + cosecθ) = 2 + secθ cosecθ
L.H.S = (sinθ + cosθ)(secθ + cosecθ)

Question 29.
(i) \(\frac { { sin }^{ 3 }A+{ cos }^{ 3 }A }{ sinA+cosA } +\frac { { sin }^{ 3 }A-{ cos }^{ 3 }A }{ sinA-cosA } =2\)
(ii) \(\frac { { tan }^{ 2 }A }{ { 1+tan }^{ 2 }A } +\frac { cot^{ 2 }A }{ 1+{ cot }^{ 2 }A } =1\)
Solution:
(i) \(\frac { { sin }^{ 3 }A+{ cos }^{ 3 }A }{ sinA+cosA } +\frac { { sin }^{ 3 }A-{ cos }^{ 3 }A }{ sinA-cosA } =2\)
L.H.S = \(\frac { { sin }^{ 3 }A+{ cos }^{ 3 }A }{ sinA+cosA } +\frac { { sin }^{ 3 }A-{ cos }^{ 3 }A }{ sinA-cosA } \)

Question 30.
(i) \(\frac { 1 }{ secA+tanA } -\frac { 1 }{ cosA } =\frac { 1 }{ cosA } -\frac { 1 }{ secA-tanA } \)
(ii) \({ (sinA+secA) }^{ 2 }+{ (cosA+cosecA) }^{ 2 }={ (1+secA\quad cosecA) }^{ 2 }\)
(iii) \(\frac { tanA+sinA }{ tanA-sinA } =\frac { secA+1 }{ secA-1 } \)
Solution:
(i) \(\frac { 1 }{ secA+tanA } -\frac { 1 }{ cosA } =\frac { 1 }{ cosA } -\frac { 1 }{ secA-tanA } \)
L.H.S = \(\frac { 1 }{ secA+tanA } -\frac { 1 }{ cosA } \)

Question 31.
If sin θ + cos θ = √2 sin (90° – θ), show that cot θ = √2 + 1
Solution:
sin θ + cos θ = √2 sin (90° – θ)
sin θ + cos θ = √2 cos θ
dividing by sin θ

Question 32.
If 7 sin² θ + 3 cos² θ = 4, 0° ≤ θ ≤ 90°, then find the value of θ.
Solution:
7 sin² θ + 3 cos² θ = 4, 0° ≤ θ ≤ 90°
3 sin² θ + 3 cos² θ + 4 sin² θ = 4

Question 33.
If sec θ + tan θ = m and sec θ – tan θ = n, prove that mn = 1.
Solution:
sec θ + tan θ = m and sec θ – tan θ = n
mn = (sec θ + tan θ) (sec θ – tan θ) = sec² θ – tan² θ = 1
(∴ sec² θ – tan² θ = 1)
Hence proved.

Question 34.
If x – a sec θ + b tan θ and y = a tan θ + b sec θ, prove that x² – y² = a² – b².
Solution:
x – a sec θ + b tan θ and y = a tan θ + b sec θ
To prove that x² – y² = a² – b².

Question 35.
If x = h + a cos θ and y = k + a sin θ, prove that (x – h)² + (y – k)² = a².
Solution:
x = h + a cos θ and y = k + a sin θ
To prove that (x – h)² + (y – k)² = a².

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances Ex 20

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances Ex 20

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances Ex 20
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances Chapter Test

Question 1.
An electric pole is 10 metres high. If its shadow is 10√3 metres in length, find the elevation of the sun.
Solution:
Let AB be the pole and
OB is its shadow.

Question 2.
The angle of elevation of the top of a tower from a point on the ground and at a distance of 150 m from its foot is 30°. Find the height of the tower correct to one place of decimal
Solution:
Let BC be the tower and
A is the point on the ground such that
∠A= 30° and AC = 150 m

Question 3.
A ladder is placed against a wall such that it just reaches the top of the wall. The foot of the ladder is 1.5 metres away from the wall and the ladder is inclined at an angle of 60° with the ground. Find the height of the wall.
Solution:
Let AB be the wall and AC be the ladder
whose foot C is 1.5 m away from B
Let AB = x m and angle of inclination is 60°

Question 4.
What is the angle of elevation of the sun when the length of the shadow of a vertical pole is equal to its height.
Solution:
Let AB be the pole and CB be its shadow
and θ is the angle of elevation of the sun.
Let AB = x m, then BC = x m

Question 5.
A river is 60 m wide. A tree of unknown height is on one bank. The angle of elevation of the top of the tree from the point exactly opposite to the foot of the tree on the other bank is 30°. Find the height of the tree.
Solution:
Let AB be the tree and BC is the width of the river
and C is the point exactly opposite to B on the other bank
and angle of elevation is 30°.

Question 6.
From a point P on level ground, the angle of elevation of the top of a tower is 30°. If the tower is 100 m high, how far is P from the foot of the tower ?
Solution:
Let AB be the tower and P is at a distance of x m from B, the foot of the tower.
While the height of the tower AB = 100 m
and angle of elevation = 30°

Question 7.
From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate to the nearest metre, the distance of the buoy from the foot of the cliff. (2005)
Solution:
Let AB be cliff whose height is 92 m
and C is buoy making depression angle of 20°.

Question 8.
A boy is flying a kite with a string of length 100 m. If the string is tight and the angle of elevation of the kite is 26°32′, find the height of the kite correct to one decimal place, (ignore the height of the boy).
Solution:
Let AB be the height of the kite A and AC is the string
and angle of elevation of the kite is 26°32′

Question 9.
An electric pole is 10 m high A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
Solution:
Let AB be the pole and AC be the wire
which makes an angle of 45° with the ground.
Height of the pole AB = 10 m
and let the length of wire AC = x m

Question 10.
A bridge across a river makes an angle of 45° with the river bank. If the length of the bridge across the river is 200 metres, what is the breadth of the river.

Solution:
Let AB be the width of river = xm
Length of the bridge AC = 200 m
and angle with the river bank = 45°
sin θ = \(\\ \frac { AB }{ AC } \)
⇒ sin 45° = \(\\ \frac { x }{ 200 } \)

Question 11.
A vertical tower is 20 m high. A man standing at some distance from the tower knows that the cosine of the angle of elevation of the top of the tower is 0.53. How far is he standing from the foot of the tower ? (2001)
Solution:
Let AB be the tower and
let a man C stands at a distance from the foot of the tower = x m
and cos θ = 0.53

Question 12.
The upper part of a tree broken by wind, falls to the ground without being detached. The top of the broken part touches the ground at an angle of 38°30′ at a point 6 m from the foot of the tree. Calculate.
(i) the height at which the tree is broken.
(ii) the original height of the tree correct to two decimal places.
Solution:
Let TR be the total height of the tree
and TP is the broken part which touches the ground
at the distance of 6 m from the foot of the tree
making an angle of 38°30′ with the ground.
Let PR = x and TR = x + y
PQ = PT = y
In right ∆PQR


Height of the tree = 4.7724 + 7.6665 = 12.4389 = 12.44 m
and height of the tree at which it is broken = 4.77 m

Question 13.
An observer 1.5 m tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
Solution:
In the figure, AB is tower and CD is an observer.
θ is the angle of observation from

Question 14.
From a boat 300 metres away from a vertical cliff, the angles of elevation of the top and the foot of a vertical concrete pillar at the edge of the cliff are 55°40′ and 54°20′ respectively. Find the height of the pillar correct to the nearest metre.

Solution:
Let CB be the cliff and AC be the pillar
and D be the boat which is 300 m away from
the foot of the cliff i.e. BD = 300 m.
Angles of elevation of the top and foot of the pillar
are 55°40′ and 54°20′ respectively.
Let CB = x and AC = y
In right ∆CBD,

Question 15.
From a point P on the ground, the angle of elevation of the top of a 10 m tall building and a helicopter hovering over the top of the building are 30° and 60° respectively. Find the height of the helicopter above the ground.
Solution:
let AB be the building and H is the helicopter hovering over it.
P is a point on the ground,
the angle of elevation of the top of building and helicopter are 30° and 60°

Question 16.
An aeroplane when flying at a height of 3125 m from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 30° and 60° respectively. Find the distance between the two planes at the instant.
Solution:
Let the distance between the two planes = h m
Given that, AD = 3125 m and ∠ACB = 60° and ∠ACD = 30°

Question 17.
A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60° ; when he retires 20 m from the bank, he finds the angle to be 30°. Find the height of the tree and the breadth of the river. .
Solution:
Let TR be the tree and PR be the width of the river.

Question 18.
The shadow of a vertical tower on a level ground increases by 10 m when the altitude of the sun changes from 45° to 30°. Find the height of the tower, correct to two decimal places. (2006)
Solution:
In the figure, AB is the tower,
BD and BC are the shadow of the tower in two situations.
Let BD = x m and AB = h m
In ∆ABD,

Question 19.
From the top of a hill, the angles of depression of two consecutive kilometer stones, due east are found to be 30° and 45° respectively. Find the distance of two stones from the foot of the hill.
Solution:
Let A and B be the position of two consecutive kilometre stones.
Then AB = 1 km = 1000m
Let the dIstance BC = x m
∴ Distance AC = (1000 + x) m

Question 20.
A man observes the angles of elevation of the top of a building to be 30°. He walks towards it in a horizontal line through its base. On covering 60 m the angle of elevation changes to 60°. Find the height of the building correct to the nearest me he.
Solution:
Given that
AB is a building CD = 60 m

Question 21.
At a point on level ground, the angle,of elevation of a vertical lower is found to be such that its tangent is \(\\ \frac { 5 }{ 12 } \). On walking 192 m towards the tower,the tangent of the angle is found to be \(\\ \frac { 3 }{ 4 } \). Find the height of the tower. (1990)
Solution:
Let TR be the tower and P is the point on the
ground such that tan θ = \(\\ \frac { 5 }{ 12 } \)

Question 22.
In the figure, not drawn to scale, TF is a tower. The elevation of T from A is x° where tan x = \(\\ \frac { 2 }{ 5 } \) and AF = 200 m. The elevation of T from B, where AB = 80 m, is y°. Calculate :
(i) The height of the tower TF.
(ii) The angle y, correct to the nearest degree. (1997)

Solution:
Let height of the tower TF = x
tan x = \(\\ \frac { 2 }{ 5 } \), AF = 200 m, AB = 80 m
(i) In right ∆ATF,

Question 23.
From the top of a church spire 96 m high, the angles of depression of two vehicles on a road, at the same level as the base of the spire and on the same side of it are x° and y°, where tan x° = \(\\ \frac { 1 }{ 4 } \) and tan y° = \(\\ \frac { 1 }{ 7 } \). Calculate the distance between the vehicles. (1994)
Solution:
Height of the church CH.
Let A and B are two vehicles which make the angle of depression
from C are x° and y° respectively.

Question 24.
In the adjoining figure, not drawn to the scale, AB is a tower and two objects C and D are located on the ground, on the same side of AB. When observed from the top A of the tower, their angles of depression are 45° and 60°. Find the distance between the two objects. If the height of the tower is 300 m. Give your answer to the nearest metre. (1998)

Solution:
Let CB = x and
DB = y
AB = 300 m

Question 25.
The horizontal distance between two towers is 140 m. The angle of elevation of the top of the first tower when seen from the top of the second tower is 30°. If the height of the second tower is 60 m, find the height of the first tower.
Solution:
Let the height of first tower TR = x
height of second tower PQ = 60 m
Distance between the two towers QR = 140 m

Question 26.
As observed from the top of a 80 m tall lighthouse, the angles of depression of two ships on the same side of the ,lighthouse in horizontal line with its base are 30° and 40° respectively. Find the distance between the two ships. Give your answer correct to the nearest metre.
Solution:
Let AB be the lighthouse and C and D be the two ships.

Question 27.
The angle of elevation of a pillar from a point A on the ground is 45° and from a point B diametrically opposite to A and on the other side of the pillar is 60°. Find the height of the pillar, given that the distance between A and B is 15 m.
Solution:
Let CD be the pillar and let CD = x
Angles of elevation of points A and B are 45° and 60° respectively.

Question 28.
From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places
Solution:
In ∆DBC, tan 60° = \(\\ \frac { 10 }{ BC } \)
⇒ √3= \(\\ \frac { 10 }{ BC } \)
⇒ BC = \(\frac { 10 }{ \sqrt { 3 } } \)
∆DBC ,tan 30° = \(\\ \frac { 10 }{ BC+AB } \)

Question 29.
(i) The angles of depression of two ships A and B as observed from the top of a light house 60 m high are 60° and 45° respectively. If the; two ships are on the opposite sides of the light house, find the distance between the two ships. Give your answer correct to the nearest whole number. (2017)
(ii) An aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number. (2014)
Solution:
(i) Let AD be the height of the lighthouse CD = 60 m
Let AD = x m, BD = y m

Question 30.
From a tower 126 m high, the angles of depression of two rocks which are in a horizontal line through the base of the tower are 16° and 12°20′ Find the distance between the rocks if they are on
(i) the same side of the tower
(ii) the opposite sides of the tower.
Solution:
Let CD be the tower and CD = 126 m
Let A and B be the two rocks on the same line
and angles of depression are 16° and 12°20′ respectively,

Question 31.
A man 1.8 m high stands at a distance of 3.6 m from a lamp post and casts a shadow of 5.4 m on the ground. Find the height of the lamp post.
Solution:
AB is the lamp post CD is the height of man.
BD is the distance of man from the foot of the lamp
and FD is the shadow of man.
CE || DB.

Question 32.
The angles of depression of the top and the bottom of an 8 m tall building from the top of a multi-storeyed building are 30° and 45° respectively. Find the height of tire multi-storeyed building and the distance between the two buildings, correct to two decimal places.
Solution:
Let AB be the CD be the building
The angles of depression in from A, to C
and D are 30° and 45° respectively
∠ACE = 30° and ∠ADB = 45°
CD = 8 m

Question 33.
A pole of height 5 m is fixed on the top of a tower. The angle of elevation of the top of the pole as observed from a point A on the ground is 60° and the angle of depression of the point A from the top of the tower is 45°. Find the height of the tower. (Take √3 = 1.732).
Solution:
Let QR be the tower and PQ be the pole on it
Angle of elevation from P to a point A is ∠PAR = 60°
and angle of depression from Q to A = 45°
∠QAR = 45° (alternate angle)
PQ = 5 m,

Question 34.
A vertical pole and a vertical tower are on the same level ground. From the top of the pole the angle of elevation of the top of the tower is 60° and the angle of depression of the foot of the tower is 30°. Find the height of the tower if the height of the pole is 20 m.
Solution:
Let TR is tower and
PL is the pole on the same level, ground PL = 20m
From P, draw PQ || LR
then ∠ TPQ = 60° and ∠ QPR = 30°

Question 35.
From the top of a building 20 m high, the angle of elevation of the top of a monumenti is 45° and the angle of depression of its foot is 15°. Find the height of the monument.
Solution:
Let AB be the building and AB = 20 m and
let CD be the monument and let CD = x
The distance between the building and the monument be y,

Question 36.
The angle of elevation of the top of an unfinished tower at a point distant 120 m from its base is 45°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60°?
Solution:
Let AB be the unfinished tower and AB = 120 m
and angle of elevation = 45°
Let x be higher raised so that
the angle of elevation becomes 60°

Question 37.
In the adjoining figure, the shadow of a vertical tower on the level ground increases by 10 m, when the altitude of the sun changes from 45° to 30°. Find the height of the tower and give your answer, correct to \(\\ \frac { 1 }{ 10 } \) of a metre.

[Remark. Altitude of the sun means angle of elevation of the sun.]
Solution:
Let TR be the tower and TR = h ;
Let BR = x,
AB = 10 m
Angles of elevation from the top of the tower
at A and B are 30° and 45° respectively.

Question 38.
An aircraft is flying at a constant height with a speed of 360 km/h. From a point on the ground, the angle of elevation of the aircraft at an instant was observed to be 45°. After 20 seconds, the angle of elevation was observed to be 30°. Determine the height at which the aircraft is flying (use √3 = 1.732)
Solution:
Speed of aircraft = 360 km/h
Distance covered in 20 seconds = \(\\ \frac { 360X20 }{ 60X60 } \) = 2 km
E is the fixed point on the ground
and CD is the position of AB in height of aircraft

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances Ex 20 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances Ex 20, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Ex 19
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Chapter Test

Question 1.
Using trigonometrical tables, find the values of :
(i) sin 48° 52′
(ii) cos 37° 34′
(iii) tan 18° 21′.
Solution:
Using tables, we find that
(i) sin 48° 52′ = .7524 + .0008 = .7532
(ii) cos 37° 34′ = .7934 – .0007 = .7927
(iii) tan 18° 21′ = .3307 + .0010 = .3317.

Question 2.
Use tables to find the acute angle θ, given that
(i) sin θ = 0.5766
(ii) cos θ = 0.2495
(iii) tan θ = 2.4523.
Solution:
Using table, we find that
(i) sin θ = 0.5766 = 0.5764 + 0.0002
= sin (35° 12’+ 1′)
= sin 35° 13′
θ = 35° 13′
(ii) cos θ = 0.2495 = 0.2487 + 0.0008
= cos (75° 36′ – 3′)
= cos 75° 33′
θ = 75° 33′
(iii) tan θ = 2.4523 = 2.4504 + 0.0019
= tan (67° 48′ + 1′)
= tan 67° 49′

Question 3.
If θ is acute and cos θ = 0.53, find the value of tan θ.
Solution:
From the table, we find that
cos θ = 0.53 = .5299 + .0001 = cos 58°
θ = 58°
and tan 58° = 1.6003

Question 4.
Find the value of: sin 22° 11′ + cos 57° 20′ – 2 tan 9° 9′.
Solution:
Using the tables, we find that
sin 22° 11′ = 0.3762 + 0.0014 = 0.3776
cos 57° 20′ = 0.5402 – 0.0005 = 0.5397
tan 9° 9′ = 0.1602 + 0.0009 = 0.1611
∴ sin 22° 11′ + cos 57° 20′ – 2 tan 9° 9′
= 0.3376 + 0.5397 – 0.1611 × 2
= 0.3776 + 0.5397 – 0.3222
= 0.9173 – 0.3222
= .5951.

Question 5.
If θ is acute and sin θ = 0.7547, find the value of: (i) θ (ii) cos θ (iii) 2 cos θ – 3 tan θ.
Solution:
Using the tables, we find that
(i) sin θ = 0.7547 = sin 49°
θ = 49°.
(ii) cos θ = cos 49° = 0.6561.
(iii) tan θ = tan 49° = 1.1504
2 cos θ – 3 tan θ
= 2 × θ.6561 – 3 × 1.1504
= 1.3122 – 3.4512
= – 2.1390

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Chapter Test help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Chapter Test, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Chapter Test

More Exercise

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Chapter Test

Question 1.
A cylindrical container is to be made of tin sheet. The height of the container is 1 m and its diameter is 70 cm. If the container is open at the top and the tin sheet costs Rs 300 per m², find the cost of the tin for making the container.
Solution:
Height of container opened at the top (h) = 1 m = 100 cm
and diameter = 70 cm
∴Radius (r) = \(\\ \frac { 70 }{ 2 } \) = 35 cm
∴Total surface area = 2πrh + πr²

Question 2.
A cylinder of maximum volume is cut out from a wooden cuboid of length 30 cm and cross-section of square of side 14 cm. Find the volume of the cylinder and the volume of wood wasted.
Solution:
Dimensions of the wooden cuboid = 30 cm × 14 cm × 14 cm
Volume = 30 × 14 × 14 = 5880 cm³

Question 3.
Find the volume and the total surface area of a cone having slant height 17 cm and base diameter 30 cm. Take π = 3.14.
Solution:
Slant height of a cone (l) = 17 cm
Diameter of base = 30 cm
Radius (r) = \(\\ \frac { 30 }{ 2 } \) = 15 cm

Question 4.
Find the volume of a cone given that its height is 8 cm and the area of base 156 cm².
Solution:
Height of a cone = 8 cm
Area of base = 156 cm
.’. Volume = \(\\ \frac { 1 }{ 3 } \) × area of base × height

Question 5.
The circumference of the edge of a hemispherical bowl is 132 cm. Find the capacity of the bowl.
Solution:
Circumference of the edge of bowl = 132 cm
Radius of a hemispherical bowl

Question 6.
The volume of a hemisphere is \(2425 \frac { 1 }{ 2 } \) cm². Find the curved surface area.
Solution:
Volume of a hemisphere = \(2425 \frac { 1 }{ 2 } \) cm³
= \(\\ \frac { 4851 }{ 2 } \) cm³
Let radius = r, then

Question 7.
A solid wooden toy is in the shape of a right circular cone mounted on a hemisphere. If the radius of the hemisphere is 4.2 cm and the total height of the toy is 10.2 cm, find the volume of the toy
Solution:
A wooden solid toy is of a shape of a right circular cone
mounted on a hemisphere.
Radius of hemisphere (r) = 4.2 cm
Total height = 10.2 cm

Question 8.
A medicine capsule is in the shape of a cylinder of diameter 0.5 cm with two hemispheres stuck to each of its ends. The length of the entire capsule is 2 cm. Find the capacity of the capsule.
Solution:
Diameter of cylindrical part = 0.5 cm
Total length of the capsule = 2 cm

Question 9.
A solid is in the form of a cylinder with hemispherical ends. The total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and the total surface area of the solid.
Solution:
Radius of cylinder = \(\\ \frac { 7 }{ 2 } \)cm
and height of cylinder = 19 – 2 × \(\\ \frac { 7 }{ 2 } \) cm
= 19 – 7 = 12 cm
and radius of hemisphere = \(\\ \frac { 7 }{ 2 } \) cm

Question 10.
The radius and height of a right circular cone are in the ratio 5 : 12. If its volume is 2512 cm , find its slant height. (Take π = 3.14).
Solution:
Let radius of cone (r) = 5x
then height (h) = 12x

Question 11.
A cone and a cylinder are of the same height. If diameters of their bases are in the ratio 3 : 2, find the ratio of their volumes.
Solution:
Let height of cone and cylinder = h
Diameter of the base of cone = 3x
Diameter of base of cylinder = 2x

Question 12.
A solid cone of base radius 9 cm and height 10 cm is lowered into a cylindrical jar of radius 10 cm, which contains water sufficient to submerge the cone completely. Find the rise in water level in the jar.
Solution:
Radius of the cone (r) = 9 cm
Height of the cone (h) = 10 cm
Volume of water filled in cone

Question 13.
An iron pillar has some part in the form of a right circular cylinder and the remaining in the form of a right circular cone. The radius of the base of each of cone and cylinder is 8 cm. The cylindrical part is 240 cm high and the conical part is 36 cm high. Find the weight of the pillar if one cu. cm of iron weighs 7.8 grams.
Solution:
Radius of the base of cone = 8 cm

Question 14.
A circus tent is made of canvas and is in the form of right circular cylinder and a right circular cone above it. The diameter and height of the cylindrical part of the tent are 126 m and 5 m respectively. The total height of the tent is 21 m. Find the total cost of the tent if the canvas used costs Rs 36 per square metre.
Solution:
Diameter of the cylindrical part = 126 m
Radius (r) = \(\\ \frac { 126 }{ 2 } \) = 63m

Question 15.
The entire surface of a solid cone of base radius 3 cm and height 4 cm is equal to the entire surface of a solid right circular cylinder of diameter 4 cm. Find the ratio of their
(i) curved surfaces
(ii) volumes.
Solution:
Radius of the base of a cone (r) = 3 cm
Height (h) = 4 cm


Question 16.
A cone is 8.4 cm high and the radius of its base is 2.1 cm. It is melted and recast into a sphere. Find the radius of the sphere.
Solution:
Radius of base of a cone (r) = 2. 1 cm
and height (h) = 8.4 cm

Question 17.
How many lead shots each of diameter 4.2 cm can be obtained from a solid rectangular lead piece with dimensions 66 cm, 42 cm and 21 cm.
Solution:
Dimensions of a solid rectangular lead piece
= 66 cm × 42 cm × 21 cm
.’. Volume = 66 × 42 × 21 cm³
Diameter of a lead shot = 4.2 cm

Question 18.
Find the least number of coins of diameter 2.5 cm and height 3 mm which are to be melted to form a solid cylinder of radius 3 cm and height 5 cm.
Solution:
Radius of a cylinder (r) = 3 cm
Height (h) = 5 cm

Question 19.
A hemisphere of lead of radius 8 cm is cast into a right circular cone of base radius 6 cm. Determine the height of the cone correct to 2 places of decimal.
Solution:
Radius of hemisphere = 8 cm
Volume = \(\frac { 2 }{ 3 } \pi { r }^{ 3 }{ cm }^{ 3 }\)

Question 20.
A vessel in the form of a hemispherical bowl is full of water. The contents are emptied into a cylinder. The internal radii of the bowl and cylinder are respectively 6 cm and 4 cm. Find the height of the water in the cylinder.
Solution:
Radius of hemispherical bowl = 6 cm
.’. Volume of the water in the bowl

Question 21.
The diameter of a metallic sphere is 42 cm. It is metled and drawn into a cylindrical wire of 28 cm diameter. Find the length of the wire.
Solution:
Diameter of sphere = 42 cm
Radius of sphere =\(\\ \frac { 42 }{ 2 } \) = 21 cm

Question 22.
A sphere of diameter 6 cm is dropped into a right circular cylindrical vessel partly filled with water. The diameter of the cylindrical vessel is 12 cm. If the sphere is completely submerged in water, by how much will the level of water rise in the cylindrical vessel?
Solution:
Radius of sphere = \(\\ \frac { 6 }{ 2 } \) = 3 cm

Question 23.
A solid sphere of radius 6 cm is metled into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 5 cm and its height is 32 cm, find the uniform thickness of the cylinder.
Solution:
Radius of solid sphere = 6 cm
Volume of solid sphere = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }\)

Question 24.
A solid is in the form of a right circular cone mounted on a hemisphere. The radius of the hemisphere is 3.5 cm and the height of the cone is 4 cm. The solid is placed in a cylindrical vessel, full of water, in such a Way that the whole solid is submerged in water. If the radius of the cylindrical vessel is 5 cm and its height is 10.5 cm, find the volume of water left in the cylindrical vessel.
Solution:
Radius of hemisphere (r) = 3.5 cm
Height of cone (h₁) = 4 cm

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Chapter Test help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Chapter Test, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Ex 19

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Ex 19

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Ex 19
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Chapter Test

Question 1.
Find the value of the following:
(i) sin 35° 22′
(ii) sin 71° 31′
(iii) sin 65° 20′
(iv) sin 23° 56′.
Solution:
(i) sin 35° 22′
Using the table of natural sines,
we see 35° in the horizontal line and for 18′,
in the vertical column, the value is 0.5779.
Now read 22′ – 18′ = 4′ in the difference column, the value is 10.
Adding 10 in 0.5779 + 10 = 0.5789,
we find sin 35° 22′ = 0.5789.
(ii) sin 71° 31′
Using the table of natural sines, we see 71° in the horizontal line
and for 30′ in the vertical column, the value is 0.9483 and for 31′ – 30′ = 1′,
we see in the mean difference column, the value is 1.
∴ sin 71° 31′ = 0.9483 + 1 = 0.9484.
(iii) sin 65° 20′
Using the table of natural sines, we see 65° in the horizontal line
and for 18′ in the vertical column, the value is .9085 and for 20′ – 18′ = 2′,
we see in the mean difference column. We find 2.
∴ sin 65° 20′ = 0.9085 + 2 = 0.9087 Ans.
(iv) sin 23° 56′
Using the table of natural sines, we see 23° in the horizontal line
and for 54′, we see in vertical column, the value is 0.4051
and for 56′ – 54′ = 2′ in the mean difference. It is 5.
∴ sin 23° 56′ = 0.4051 + 5 = 0.4056

Question 2.
Find the value of the following:
(i) cos 62° 27′
(ii) cos 3° 11′
(iii) cos 86° 40′
(iv) cos 45° 58′.
Solution:
(i) cos 62° 27′
From the table of natural cosines,
we see 62° in the horizontal line and 24′ in the vertical column, the value is .4633
and 27′ – 24′ = 3′ in the mean difference. Its value is 8.
∴ cos 62° 27′ = 0.4633 – 8 = 0.4625 Ans.
(ii) cos 3° 11′
From the table of natural cosines, we see 3° in the horizontal line
and 6′ in the vertical column, its value is 0.9985
and 11′ – 6′ = 5′ in the mean difference, its value is 1.
∴ cos 3° 11′ = 0.9985 – 1 = 0.9984 Ans.
(iii) cos 86° 40′
From the table of natural cosines, we see 86° in the horizontal line
and 36′ in the vertical column, its value is 0.0593
and for 40′ – 36′ = 4′ in the mean difference, it is 12.
cos 86° 40’= 0.0593 – 12 = 0 0581 Ans.
(iv) cos 45° 58′
From the table of natural cosines, we see 45° in the horizontal column
and 54′ in the vertical column, its value is 0.6959
and for 58′ – 54′ = 4′, in the mean difference, it is 8.’
cos 45° 58′ = 0.6959 – 8 = 0.6951

Question 3.
Find the value of the following :
(i) tan 15° 2′
(ii) tan 53° 14′
(iii) tan 82° 18′
(iv) tan 6° 9′.
Solution:
(i) tan 15° 2′
From the table of natural tangents, we see 15° in the horizontal line,
its value is 0.2679 and for 2′, in the mean difference, it is 6.
tan 15° 2′ = 0.2679 + 6 = 0.2685.
(ii) tan 53° 14′
From the table of natural tangents, we see 53° in the horizontal line
and 12′ in the vertical column, its value is 1.3367
and 14′ – 12′ = 2′ in the mean difference, it is 16.
∴ tan 53° 14′ = 1.3367 + 16 = 1 .3383 Ans.
(iii) tan 82° 18′
From the table of natural tangents, we see 82° in the horizontal line
and 18′ in the vertical column, its value is 7.3962.
∴ tan 82° 18’= 7.3962.
(iv) tan 6° 9′
From the table of natural tangents, we see 6° in the horizontal line
and 6′ in the vertical column, its value is .1069
and 9′ – 6′ = 3′, in the mean difference, it is 9.
tan 6°9′ = .1069 + 9 = .1078.

Question 4.
Use tables to find the acute angle θ, given that:
(i) sin θ = – 5789
(ii) sin θ = – 9484
(iii) sin θ = – 2357
(iv) sin θ = – 6371.
Solution:
(i) sin θ = – 5789
From the table of natural sines,
we look for the value (≤ 5789), which must be very close to it,
we find the value .5779 in the column 35° 18′ and in mean difference,
we see .5789 – .5779 = .0010 in the column of 4′.
θ = 35° 18’+ 4’= 35° 22′ Ans.
(ii) sin θ = . 9484
From the table of natural sines,
we look for the value (≤ 9484) which must be very close to it,
we find the value .9483 in the column 71° 30′
and in the mean differences,
we see .9484 – 9483 = 0001, in the column of 1′.
θ = 71° 30′ + 1′ = 71° 31′ Ans.
(iii) sin θ = – 2357
From the table of natural sines,
we look for the value (≤ 2357) which must be very close to it,
we find the value .2351 in the column 13° 36′ and in the mean difference,
we see .2357 – 2351 = .0006, in the column of 2′.
θ = 13° 36′ +2’= 13° 38′ Ans.
(iv) sin θ = .6371
From the table of natural sines,
we look for the value (≤ 6371) which must be very close to it,
we find the value .6361 in the column 39° 30′ and in the mean difference,
we see .6371 – .6361 = .0010 in the column of 4′.
θ = 39° 30′ + 4′ = 39° 34′

Question 5.
Use the tables to find the acute angle θ, given that:
(i) cos θ = .4625
(ii) cos θ = .9906
(iii) cos θ = .6951
(iv) cos θ = .3412.
Solution:
(i) cos θ = .4625
From the table of natural cosines,
we look for the value (≤ .4625) which must be very close to it,
we find the value .4617 in the column of 62° 30′ and in the mean difference,
we see .4625 – .4617 = .0008 which is in column of 3′.
θ = 62° 30′ – 3’= 62° 27′.
(ii) cos θ = .9906
From the table of cosines,
we look for the value (≤ .9906) which must be very close to it,
we find the value of .9905 in the column of 7° 54′ and in mean difference,
we see .9906 – 9905 = .0001 which is in column of 3′.
θ = 70 54′ – 3’= 7° 51′
(iii) cos θ = .6951
From the tables of cosines,
we look for the value (≤ 6951) which must be very close to it,
we find the value .6947 in the column of 46° and in mean difference,
.6951 – .6947 = 0.0004 which in the column of 2′.
θ = 46° – 2′ = 45° 58′ Ans.
(iv) cos θ = .3412
From the table of cosines,
we look for the value of (≤ .3412) which must be very close to it,
we find the value .3404 in the column of 70° 6′ and in the mean difference,
.3412 – 3404 = .0008 which is in the column of 3′.
θ = 70° 6′ – 3′ = 70° 3′

Question 6.
Use tables to find the acute angle θ, given that:
(i) tan θ = .2685
(ii) tan θ = 1.7451
(iii) tan θ = 3.1749
(iv) tan θ = .9347
Solution:
(i) tan θ = .2685
From the table of natural tangent,
we look for the value of (≤ .2685) which must be very close to it,
we find the value .2679 in the column of 15° and in the mean difference,
.2685 – .2679 which is in the column of 2′.
θ = 15° +2′ = 15° 2′ Ans.
(ii) tan θ = 1.7451
From the tables of natural tangents,
we look for the value of (≤ 1.7451) which must be very close to it,
we find the value 1.7391 in the column of 60°’ 6′
and in the mean difference 1.7451 + 1.7391 = 0.0060 which is in the column of 5′.
θ = 60° 6’+ 5’= 60° 11’Ans.
(iii) tan θ = 3.1749
From the tables of natural tangents,
we look for the value of (≤ 3.1749) which must be very close to it,
we find the value 3.1716 in the column of 72° 30′
and in the mean difference 3.1749 – 3.1716 = 0.0033 which is in the column of 1′.
θ = 720 30′ + 1′ = 72° 31′ Ans.
(iv) tan θ = .9347
From the tables of natural tangents,
we look for the value of (≤ .9347 which must be very close to it,
we find the value .9325 in the column of 43°
and in the mean difference .9347 – .9325 = 0.0022 which is in the column of 4′.
θ = 43° + 4′ = 43° 4′

Question 7.
Using trigonometric table, find the measure of the angle A when sin A = 0.1822.
Solution:
sin A = 0.1822
From the tables of natural sines,
we look for the value (≤ .1822) which must be very close to it,
we find the value .1822 in column 10° 30′.
A = 10° 30′

Question 8.
Using tables, find the value of 2 sin θ – cos θ when (i) θ = 35° (ii) tan θ = .2679.
Solution:
(i) θ = 35°
2 sin θ – cos θ = 2 sin 35° – cos 35°
= 2 x .5736 – .8192
(From the tables)
= 1.1472 – .8192 = 0.3280.
(ii) tan θ = .2679
From the tables of natural tangents,
we look for the value of ≤ .2679,
we find the value of the column 15°.
θ = 15°
Now, 2 sin θ – cos θ = 2 sin 15° – cos 15°
= 2 (.2588) – .9659 = 5136 – .9659
= -0.4483

Question 9.
If sin x° = 0.67, find the value of
(i) cos x°
(ii) cos x° + tan x°.
Solution:
sin x° = 0.67
From the table of natural sines,
we look for the value of (≤ 0.67) which must be very close to it,
we find the value .6691 in the column 42° and in the mean difference,
the value of 0.6700 – 0.6691 = 0.0009 which is in the column 4′.
θ = 42° + 4′ = 42° 4′
Now
(i) cos x° = cos 42° 4′ = .7431 – .0008
= 0.7423 Ans.
(ii) cos x° + tan x° = cos 42° 4′ + tan 42° 4′
= 0.7423 + .9025
= 1.6448

Question 10.
If θ is acute and cos θ = .7258, find the value of (i) θ (ii) 2 tan θ – sin θ.
Solution:
cos θ = .7258
From the table of cosines,
we look for the value of (≤ .7258) which must be very close to it,
we find the value .7254 in the column of 43° 30′
and in the mean differences the value of .7258 – .7254 = 0.0004
which in the column of 2′.
(i) θ = 43° 30′ – 2’= 43° 28′.
(ii) 2 tan θ – sin θ
= 2 tan43°28′ – sin43°28′
= 2 (.9479) – .6879
= 1.8958 – .6879
= 1.2079

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Ex 19 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 19 Trigonometric Tables Ex 19, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test

Question 1.
Draw an ogive for the following frequency distribution:

Solution:

Plot the points (160, 8), (170, 11), (180, 15), (190, 25) and (200, 27)
on the graph and join them with the free hand. We get an ogive as shown:

Question 2.
Draw an ogive for the following data:

Solution:

Plot the points (10.5, 3), (20.5, 8), (30.5, 16), (40.5, 23),
(50.5, 29), (60.5, 31) on the graph and join them with a free hand,
we get an ogive as shown:

Question 3.
Draw a cumulative frequency curve for the following data:

Solution:

Plot the points (29, 1), (34, 3), (39, 8), (44, 14), (49, 18),
(54, 21) and (59, 23) on the graph and join them
with a free hand to get an ogive as shown:

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test

Question 1.
A student scored the following marks in 11 questions of a question paper : 3, 4, 7, 2, 5, 6, 1, 8, 2, 5, 7 Find the median marks.
Solution:
Arranging in the ascending order, 1, 2, 2, 3, 4, 5, 5, 6, 7, 7, 8
Here, n = 11 i.e. odd,
The middle term = \(\\ \frac { n+1 }{ 2 } \) = \(\\ \frac { 11+1 }{ 2 } \) = \(\\ \frac { 12 }{ 2 } \) = 6th term
Median = 5

Question 2.
(a) Find the median of the following set of numbers : 9, 0, 2, 8, 5, 3, 5, 4, 1, 5, 2, 7 (1990)
(b)For the following set of numbers, find the median: 10, 75, 3, 81, 17, 27, 4, 48, 12, 47, 9, 15.
Solution:
(a) Arranging in ascending order :
0, 1, 2, 2, 3, 4, 5, 5, 5, 7, 8, 9
Here, n = 12 which is even

Question 3.
Calculate the mean and the median of the numbers : 2, 1, 0, 3, 1, 2, 3, 4, 3, 5
Solution:
Writing in ascending order 0, 1, 1, 2, 2, 3, 3, 3, 4, 5
Here, n = 10 which is even

Question 4.
The median of the observations 11, 12, 14, (x – 2), (x + 4), (x + 9), 32, 38, 47 arranged in ascending order is 24. Find the value of x and hence find the mean.
Solution:
Observation are :
11, 12, 14, (x – 2), (x + 4), (x + 9), 32, 38, 47
n = 9
Median = \(\\ \frac { 9+1 }{ 2 } \) th term
i.e, 5th term = x + 4

Question 5.
The mean of the numbers 1, 7, 5, 3, 4, 4, is m. The numbers 3, 2, 4, 2, 3, 3, p have mean m – 1 and median q. Find
(i) p
(ii) q
(iii) the mean of p and q.
Solution:
(i) Mean of 1, 7, 5, 3, 4, 4 is m.
Here n = 6

Question 6.
Find the median for the following distribution:

Solution:
Writing the distribution in cumulative frequency table:

Question 7.
Find the median for the following distribution.

Solution:
Writing the distribution in cumulative frequency table :

Question 8.
Marks obtained by 70 students are given below :

Calculate the median marks.
Solution:
Arranging the variates in ascending order and in c.f. table.

Question 9.
Calculate the mean and the median for the following distribution :

Solution:
Writing the distribution in c.f. table :

Question 10.
The daily wages (in rupees) of 19 workers are
41, 21, 38, 27, 31, 45, 23, 26, 29, 30, 28, 25, 35, 42, 47, 53, 29, 31, 35.
Find
(i) the median
(ii) lower quartile
(iii) upper quartile range,
(iv) interquartile range.
Solution:
Arranging the observations in ascending order
21, 23, 25, 26, 27, 28, 29, 29, 30, 31, 31, 35, 35, 38, 41, 42, 45, 47, 53
Here n = 19 which is odd.
(i) Median = \(\\ \frac { n+1 }{ 2 } \) th term = \(\\ \frac { 19+1 }{ 2 } \) = \(\\ \frac { 20 }{ 2 } \) = 10th term = 31

Question 11.
From the following frequency distribution, find :
(i) the median
(ii) lower quartile
(iii) upper quartile
(iv) inter quartile range

Solution:
Writing frequency distribution in c.f. table :

Question 12.
For the following frequency distribution, find :
(i) the median
(ii) lower quartile
(iii) upper quartile

Solution:
Writing the distribution in cumulative frequency (c.f.) table :

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS

More Exercise

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Chapter Test

Choose the correct answer from the given four options (1 to 32) :

Question 1.
In a cylinder, if radius is halved and height is doubled then the volume will be
(a) same
(b) doubled
(c) halved
(d) four times
Solution:
Let radius of cylinder = r
and height = h
then volume = πr²h
If the radius is halved and the height is doubled

Question 2.
In a cylinder, if the radius is doubled &nd height is halved then its curved surface area will be
(a) halved
(b) doubled
(c) same
(d) four times
Solution:
Let radius of a cylinder = r
and height = h
Then curved surface area = 2πrh
Now if radius is doubled and height is halved,
then curved surface area = 2π\(\\ \frac { r }{ 2 } \) × 2h = 2πrh
which is same (c)

Question 3.
If a well of diameter 8 m has been dug to the depth of 14 m, then the volume of the earth dug out is
(a) 352 m³
(b) 704 m³
(c) 1408 m³
(d) 2816 m³
Solution:
Diameter of a well = 8 m
Radius (r) = \(\\ \frac { 8 }{ 2 } \) = 4m
Depth (h) = 14 m
Volume of the earth dug put = πr²h
= \(\\ \frac { 22 }{ 7 } \) × 4 × 4 × 14 m³
= 704 m³ (b)

Question 4.
If two cylinders of the same lateral surface have their radii in the ratio 4 : 9, then the ratio of their heights is
(a) 2 : 3
(b) 3 : 2
(c) 4 : 9
(d) 9 : 4
Solution:
Ratio in two cylinder having same lateral surface area their radii is 4 : 9
Let r₁ be the radius of the first and r₂ be the second cylinder
and h₁, h₂ and their heights

Ratio in their heights = 9 : 4 (d)

Question 5.
The radii of two cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 3. The ratio of their volumes is
(a) 10 : 17
(b) 20 : 27
(c) 17 : 27
(d) 20 : 37
Solution:
Radii of two cylinder are in the ratio = 2 : 3
Let radius (r₁) = 2x
and radius (r₂) = 3x
Ratio in their height = 5 : 3
Let height of the first cylinder = 5y
and of second = 3y
Now, volume of the first cylinder

Question 6.
The total surface area of a cone whose radius is \(\\ \frac { r }{ 2 } \) and slant height 2l is
(a) 2πr (l + r)
(b) \(\pi r\left( l+\frac { r }{ 4 } \right) \)
(c) πr(l + r)
(d) 2πrl
Solution:
Radius of a cone = \(\\ \frac { r }{ 2 } \)
and slant height = 2l
total surface area of a cone

Question 7.
If the diameter of the base of cone is 10 cm and its height is 12 cm, then its curved surface area is
(a) 60π cm²
(b) 65π cm²
(c) 90π cm²
(d) 120π cm²
Solution:
Diameter of the base of a cone = 10 cm
Radius (r) = \(\\ \frac { 10 }{ 2 } \) = 5 cm
and height (h) = 12 cm

Question 8.
If the diameter of the base of a cone is 12 cm and height is 20 cm, then its volume is ,
(a) 240π cm³
(b) 480π cm³
(c) 720π cm³
(d) 960π cm³
Solution:
Diameter of the base of a cone = 12 cm
Radius (r) = \(\\ \frac { 12 }{ 2 } \) = 6 cm
and height (h) = 20 cm

Question 9.
If the radius of a sphere is 2r, then its volume will be
(a) \(\frac { 4 }{ 3 } \pi { r }^{ 3 } \)
(b) \(4\pi { r }^{ 3 }\)
(c) \(\frac { 8\pi { r }^{ 3 } }{ 3 } \)
(d) \(\frac { 32\pi { r }^{ 3 } }{ 3 } \)
Solution:
Radius of a sphere = 2r

Question 10.
If the diameter of a sphere is 16 cm, then its surface area is
(a) 64π cm²
(b) 256π cm²
(c) 192π cm²
(d) 256 cm²
Solution:
Diameter of a sphere = 16 cm
Radius (r) = \(\\ \frac { 16 }{ 2 } \) = 8 cm
Surface area = 4π² = 4π × 8 × 8 cm² = 256π cm² (b)

Question 11.
If the radius of a hemisphere is 5 cm, then its volume is
(a) \(\frac { 250 }{ 3 } \pi { \quad cm }^{ 3 }\)
(b) \(\frac { 500 }{ 3 } \pi { \quad cm }^{ 3 } \)
(c) \(75\pi { \quad cm }^{ 3 } \)
(d) \(\frac { 125 }{ 3 } \pi { \quad cm }^{ 3 } \)
Solution:
Radius of a hemisphere (r) = 5 cm

Question 12.
If the ratio of the diameters of the two spheres is 3 : 5, then the ratio of their surface areas is
(a) 3 : 5
(b) 5 : 3
(c) 27 : 125
(d) 9 : 25
Solution:
Ratio in the diameters of two spheres = 3 : 5
Let radius of the first sphere = 3x cm
and radius of the second sphere = 5x cm
Ratio in their surface area

Question 13.
The radius of a hemispherical balloon increases from 6 cm to 12 cm as air is being pumped into it. The ratio of the surface areas of the balloon in the two cases is
(a) 1 : 4
(b) 1 : 3
(c) 2 : 3
(d) 2 : 1
Solution:
Radius of balloon (hemispherical) in the original position = 6 cm
and in increased position = 12 cm
Ratio in their surface areas

Question 14.
The shape of a Gilli, in the game of Gilli- danda, is a combination of

(a) two cylinders
(b) a cone and a cylinders
(c) two cones and a cylinder
(d) two cylinders and a cone
Solution:
The shape of a Gilli is the combination of
two cones and a cylinder (as shown in the figure). (c)

Question 15.
If two solid hemisphere of same base radius r are joined together along with their bases, then the curved surface of this new solid is
(a) 4πr²
(b) 6πr²
(c) 3πr²
(d) 8πr²
Solution:
Radius of two solid hemispheres = r
These are joined together along with the bases
Curved surface area = 2π² × 2 = 4πr² (a)

Question 16.
During conversion of a solid from one shape to another, the volume of the new shape will
(a) increase
(b) decrease
(c) remain unaltered
(d) be doubled
Solution:
During the conversion of a solid into another,
the volume of the new shaper will be the same.
i.e. remain unaltered (c)

Question 17.
If a solid of one shape is converted to another, then the surface area of the new solid
(a) remains same
(b) increases
(c) decreases
(d) can’t say
Solution:
If a solid of one shape has conversed into another then
the surface area of the new solid will same or not same
i.e. can’t say. (d)

Question 18.
If a marble of radius 2.1 cm is put into a cylindrical cup full of water of radius 5 cm and height 6 cm, then the volume of water that flows out of the cylindrical cup is
(a) 38.8 cm³
(b) 55.4 cm³
(c) 19.4 cm³
(d) 471.4 cm³
Solution:
Radius of a marble = 2.1 cm
Volume of marble = \(\frac { 4 }{ 3 } \pi { { r }^{ 3 }\quad cm }^{ 3 }\)
= \(\\ \frac { 4 }{ 3 } \) x \(\\ \frac { 22 }{ 7 } \) × 2.1 × 2.1 × 2.1 cm³
= 38.88 cm³
= 38.8 cm³ (a)

Question 19.
The volume of the largest right circular cone that can be carved out from a cube of edge 4.2 cm is
(a) 9.7 cm³
(b) 77.6 cm³
(c) 58.2 cm³
(d) 19.4 cm³
Solution:
Edge of cube = 4.2 cm
Radius of largest cone cut out = \(\\ \frac { 42.2 }{ 2 } \) = 2.1 cm
and height = 4.2 cm
Volume = \(\frac { 1 }{ 3 } \pi { { r }^{ 2 }h } \)
= \(\\ \frac { 1 }{ 3 } \) x \(\\ \frac { 22 }{ 7 } \) × 2.1 × 2.1 × 4.2 cm³
= 19.404
= 19.4 cm³ (d)

Question 20.
The volume of the greatest sphere cut off from a circular cylindrical wood of base radius 1 cm and height 6 cm is
(a) 288 π cm³
(b) \(\frac { 4 }{ 3 } \pi \) cm³
(c) 6 π cm³
(d) 4 π cm³
Solution:
Radius of cylinder (r) = 1 cm
Height (h) = 6 cm
The largest sphere that can be cut off from the cylinder of radius 1 cm

Question 21.
The volumes of two spheres are in the ratio 64 : 27. The ratio of their surface areas is
(a) 3 : 4
(b) 4 : 3
(c) 9 : 16
(d) 16 : 9
Solution:
Ratio in volumes of two spheres = 64 : 27

Question 22.
If a cone, a hemisphere and a cylinder have equal bases and have same height, then the ratio of their volumes is
(a) 1 : 3 : 2
(b) 2 : 3 : 1
(c) 2 : 1 : 3
(d) 1 : 2 : 3
Solution:
If a cone, a hemisphere and a cylinder have equal bases = r (say)
and height = h in each case and r = h

Question 23.
If a sphere and a cube have equal surface areas, then the ratio of the diameter of the sphere to the edge of the cube is
(a) 1 : 2
(b) 2 : 1
(c) √π : √6
(d) √6 : √π
Solution:
A sphere and a cube have equal surface area
Let a be the edge of a cube and r be the radius of the sphere, then

Question 24.
A solid piece of iron in the form of a cuboid of dimensions 49 cm x 33 cm x 24 cm is moulded to form a sphere. The radius of the sphere is
(a) 21 cm
(b) 23 cm
(c) 25 cm
(d) 19 cm
Solution:
Dimension of a cuboid = 49 cm × 33 cm × 24 cm
Volume of a cuboid = 49 × 33 × 24 cm³
⇒ Volume of sphere = Volume of a cuboid
Volume of a sphere = 49 × 33 × 24 cm³

Question 25.
If a solid right circular cone of height 24 cm and base radius 6 cm is melted and recast in the shape of a sphere, then the radius of the sphere is
(a) 4 cm
(b) 6 cm
(c) 8 cm
(d) 12 cm
Solution:
Height of a circular cone (h) = 24 cm
and radius (r) = 6 cm

Question 26.
If a solid circular cylinder of iron whose diameter is 15 cm and height 10 cm is melted and recasted into a sphere, then the radius of the sphere is
(a) 15 cm
(b) 10 cm
(c) 7.5 cm
(d) 5 cm
Solution:
Diameter of a cylinder = 15 cm
Radius = \(\\ \frac { 15 }{ 2 } \) cm
and height = 10 cm

Question 27.
The number of balls of radius 1 cm that can be made from a sphere of radius 10 cm is
(a) 100
(b) 1000
(c) 10000
(d) 100000
Solution:
Radius of sphere (R) = 10 cm
Volume of sphere = \(\frac { 4 }{ 3 } \pi { R }^{ 3 }=\frac { 4 }{ 3 } \pi { (10) }^{ 3 }{ cm }^{ 3 }\)

Question 28.
A metallic spherical shell of internal and external diameters 4 cm and 8 cm, respectively is melted and recast into the form of a cone of base diameter 8 cm. The height of the cone is
(a) 12 cm
(b) 14 cm
(c) 15 cm
(d) 18 cm
Solution:
The internal diameter of the metallic shell = 4 cm
and external diameter = 8 cm

Question 29.
A cubical icecream brick of edge 22 cm is to be distributed among some children by filling icecream cones of radius 2 cm and height 7 cm upto its brim. The number of children who will get the icecream cones is
(a) 163
(b) 263
(c) 363
(d) 463
Solution:
Edge of a cubical icecream brick = 22 cm
Volume = a³ = (22)³ = 10648 cm³
Radius (r) of ice cream cone (r) = 2 cm
and height (h) = 7 cm

Question 30.
Twelve solid spheres of the same size are made by melting a solid metallic cylinder of base diameter 2 cm and height 16 cm. The diameter of each sphere is
(a) 4 cm
(b) 3 cm
(b) 2 cm
(d) 6 cm
Solution:
Diameter of cylinder = 2 cm
Radius = \(\\ \frac { 2 }{ 2 } \) = 1 cm
and height = 16 cm

Question 31.
A hollow cube of internal edge 22 cm is filled with spherical marbles of diameter 0.5 cm and it is assumed that \(\\ \frac { 1 }{ 8 } \) space of the cube remains unfilled. Then the number of marbles that the cube can accommodate is
(a) 142296
(b) 142396
(c) 142496
(d) 142596
Solution:
Internal edge of a hollow cube = 22 cm
Volume = (side)³ = (22)³ = 22 × 22 × 22 cm³ = 10648 cm³
Diameter of spherical marble = 0.5 cm = \(\\ \frac { 1 }{ 2 } \)

Question 32.
In the given figure, the bottom of the glass has a hemispherical raised portion. If the glass is filled with orange juice, the quantity of juice which a person will get is
(a) 135 π cm³
(b) 117 π cm³
(c) 99 π cm³
(d) 36 π cm³

Solution:
Radius of base of cylinder (r) = \(\\ \frac { 6 }{ 2 } \) cm = 3 cm
and height (h)= 15 cm

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test

Question 1.
(i) If θ is an acute angle and cosec θ = √5 find the value of cot θ – cos θ.
(ii) If θ is an acute angle and tan θ = \(\\ \frac { 8 }{ 15 } \), find the value of sec θ + cosec θ.
Solution:
(i) θ is an acute angle.
cosec θ = √5

Question 2.
Evaluate the following:
(i) \(2\times \left( \frac { { cos }^{ 2 }{ 20 }^{ O }+{ cos }^{ 2 }{ 70 }^{ O } }{ { sin }^{ 2 }{ 25 }^{ O }+{ sin }^{ 2 }{ 65 }^{ O } } \right) \) – tan 45° + tan 13° tan 23° tan 30° tan 67° tan 77°
(ii) \(\frac { { sec }29^{ O } }{ { cosec }61^{ O } } \) + 2 cot 8° cot 17° cot 45° cot 73°0 cot 82° – 3(sin2 38° + sin2 52°)
(iii) \(\frac { { sin }^{ 2 }{ 22 }^{ O }+{ sin }^{ 2 }{ 68 }^{ O } }{ { cos }^{ 2 }{ 22 }^{ O }+{ cos }^{ 2 }{ 68 }^{ O } } \) + sin2 63° + cos 63° sin 27°
Solution:
(i) \(2\times \left( \frac { { cos }^{ 2 }{ 20 }^{ O }+{ cos }^{ 2 }{ 70 }^{ O } }{ { sin }^{ 2 }{ 25 }^{ O }+{ sin }^{ 2 }{ 65 }^{ O } } \right) \) – tan 45° + tan 13° tan 23° tan 30° tan 67° tan 77°

Question 3.
If \(\\ \frac { 4 }{ 3 } \) (sec2 59° – cot2 31°) – \(\\ \frac { 2 }{ 2 } \) sin 90° + 3tan2 56° tan2 34° = \(\\ \frac { x }{ 2 } \), then find the value of x.
Solution:
Given
\(\\ \frac { 4 }{ 3 } \) (sec2 59° – cot2 31°) – \(\\ \frac { 2 }{ 2 } \) sin 90° + 3tan2 56° tan2 34° = \(\\ \frac { x }{ 2 } \)

Prove the following (4 to 11) identities, where the angles involved are acute angles for which the trigonometric ratios are defined:

Question 4.
(i) \(\frac { cosA }{ 1-sinA } +\frac { cosA }{ 1+sinA } =2secA \)
(ii) \(\frac { cosA }{ cosecA+1 } +\frac { cosA }{ cosecA-1 } =2tanA \)
Solution:
(i) \(\frac { cosA }{ 1-sinA } +\frac { cosA }{ 1+sinA } =2secA \)
L.H.S = \(\frac { cosA }{ 1-sinA } +\frac { cosA }{ 1+sinA } \)

Question 5.
(i) \(\frac { (cos\theta -sin\theta )(1+tan\theta ) }{ 2{ cos }^{ 2 }\theta -1 } =sec\theta \)
(ii) (cosec θ – sin θ) (sec θ – cos θ) (tan θ + cot θ) = 1.
Solution:
(i) \(\frac { (cos\theta -sin\theta )(1+tan\theta ) }{ 2{ cos }^{ 2 }\theta -1 } =sec\theta \)
L.H.S = \(\frac { (cos\theta -sin\theta )(1+tan\theta ) }{ 2{ cos }^{ 2 }\theta -1 } \)

Question 6.
(i) sin² θ + cos⁴ θ = cos² θ + sin⁴ θ
(ii) \(\frac { cot\theta }{ cosec\theta +1 } +\frac { cosec\theta +1 }{ cot\theta } =2sec\theta \)
Solution:
L.H.S. = sin² θ + cos⁴ θ
= (1 – cos² θ + cos⁴ θ
= 1 – cos² θ + cos⁴ θ
= 1 – cos² θ (1 – cos² θ)

Question 7.
(i) sec⁴ A (1 – sin⁴ A) – 2 tan² A = 1
(ii) \(\frac { 1 }{ sinA+cosA+1 } +\frac { 1 }{ sinA+cosA-1 } =secA+cosecA\)
Solution:
(i) sec⁴ A (1 – sin⁴ A) – 2 tan² A = 1
L.H.S = sec⁴ A (1 – sin⁴ A) – 2 tan² A

Question 8.
(i) \(\frac { { sin }^{ 3 }\theta +{ cos }^{ 3 }\theta }{ sin\theta cos\theta } +sin\theta cos\theta =1\)
(ii) (sec A – tan A)² (1 + sin A) = 1 – sin A.
Solution:
(i) \(\frac { { sin }^{ 3 }\theta +{ cos }^{ 3 }\theta }{ sin\theta cos\theta } +sin\theta cos\theta =1\)
L.H.S = \(\frac { { sin }^{ 3 }\theta +{ cos }^{ 3 }\theta }{ sin\theta cos\theta } +sin\theta cos\theta\)

Question 9.
(i) \(\frac { cosA }{ 1-tanA } -\frac { { sin }^{ 2 }A }{ cosA-sinA } =sinA+cosA \)
(ii) (sec A – cosec A) (1 + tan A + cot A) = tan A sec A – cot A cosec A
(iii) \(\frac { { tan }^{ 2 }\theta }{ { tan }^{ 2 }\theta -1 } -\frac { { cosec }^{ 2 }\theta }{ { sec }^{ 2 }\theta -{ cosec }^{ 2 }\theta } =\frac { 1 }{ { sin }^{ 2 }\theta -{ cos }^{ 2 }\theta } \)
Solution:
(i) \(\frac { cosA }{ 1-tanA } -\frac { { sin }^{ 2 }A }{ cosA-sinA } =sinA+cosA \)
L.H.S = \(\frac { cosA }{ 1-tanA } -\frac { { sin }^{ 2 }A }{ cosA-sinA } \)

Question 10.
\(\frac { sinA+cosA }{ sinA-cosA } +\frac { sinA-cosA }{ sinA+cosA } =\frac { 2 }{ { sin }^{ 2 }A-{ cos }^{ 2 }A } =\frac { 2 }{ 1-2{ cos }^{ 2 }A } =\frac { { 2sec }^{ 2 }A }{ { tan }^{ 2 }A-1 } \)
Solution:
\(\frac { sinA+cosA }{ sinA-cosA } +\frac { sinA-cosA }{ sinA+cosA } =\frac { 2 }{ { sin }^{ 2 }A-{ cos }^{ 2 }A } =\frac { 2 }{ 1-2{ cos }^{ 2 }A } =\frac { { 2sec }^{ 2 }A }{ { tan }^{ 2 }A-1 } \)
L.H.S = \(\frac { sinA+cosA }{ sinA-cosA } +\frac { sinA-cosA }{ sinA+cosA } \)

Question 11.
2 (sin⁶ θ + cos⁶ θ) – 3 (sin⁴ θ + cos⁴ θ) + 1 = θ
Solution:
2 (sin⁶ θ + cos⁶ θ) – 3 (sin⁴ θ + cos⁴ θ) + 1 = θ
L.H.S = 2 (sin⁶ θ + cos⁶ θ) – 3 (sin⁴ θ + cos⁴ θ) + 1

Question 12.
If cot θ + cos θ = m, cot θ – cos θ = n, then prove that (m² – n²)² = 16 run.
Solution:
cot θ + cos θ = m…..(i)
cot θ – cos θ = n……(ii)
Adding (i)&(ii) we get

Question 13.
If sec θ + tan θ = p, prove that sin θ = \(\frac { { p }^{ 2 }-1 }{ { p }^{ 2 }+1 } \)
Solution:
sec θ + tan θ = p,
prove that sin θ = \(\frac { { p }^{ 2 }-1 }{ { p }^{ 2 }+1 } \)
\(\frac { 1 }{ cos\theta } +\frac { sin\theta }{ cos\theta } =p\)

Question 14.
If tan A = n tan B and sin A = m sin B, prove that cos² A = \(\frac { { m }^{ 2 }-1 }{ { n }^{ 2 }-1 } \)
Solution:
m = \(\\ \frac { sinA }{ sinB } \)
n = \(\\ \frac { tanA }{ tanB } \)

Question 15.
If sec A = \(x+ \frac { 1 }{ 4x } \), then prove that sec A + tan A = 2x or \(\\ \frac { 1 }{ 2x } \)
Solution:
sec A = \(x+ \frac { 1 }{ 4x } \)
To prove that sec A + tan A = 2x or \(\\ \frac { 1 }{ 2x } \)

Question 16.
When 0° < θ < 90°, solve the following equations:
(i) 2 cos² θ + sin θ – 2 = 0
(ii) 3 cos θ = 2 sin² θ
(iii) sec² θ – 2 tan θ = 0
(iv) tan² θ = 3 (sec θ – 1).
Solution:
0° < θ < 90°
(i) 2 cos² θ + sin θ – 2 = 0

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Ex 18
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities Chapter Test

Choose the correct answer from the given four options (1 to 12) :

Question 1.
\({ cot }^{ 2 }\theta -\frac { 1 }{ { sin }^{ 2 }\theta } \) is equal to
(a) 1
(b) -1
(c) sin² θ
(d) sec² θ
Solution:
\({ cot }^{ 2 }\theta -\frac { 1 }{ { sin }^{ 2 }\theta } \)
= \(\frac { { cos }^{ 2 }\theta }{ { sin }^{ 2 }\theta } -\frac { 1 }{ { sin }^{ 2 }\theta } \)

Question 2.
(sec² θ – 1) (1 – cosec² θ) is equal to
(a) – 1
(b) 1
(c) 0
(d) 2
Solution:
(sec² θ – 1) (1 – cosec² θ)
= \(\left( \frac { 1 }{ { cos }^{ 2 }\theta } -1 \right) \left( 1-\frac { 1 }{ { sin }^{ 2 }\theta } \right) \)

Question 3.
\(\frac { { tan }^{ 2 }\theta }{ 1+{ tan }^{ 2 }\theta } \) is equal to
(a) 2 sin² θ
(b) 2 cos² θ
(c) sin² θ
(d) cos² θ
Solution:
\(\frac { { tan }^{ 2 }\theta }{ 1+{ tan }^{ 2 }\theta } \)

= \(=\frac { { sin }^{ 2 }\theta }{ 1 } ={ sin }^{ 2 }\theta \) (c)

Question 4.
(cos θ + sin θ)² + (cos θ – sin θ)² is equal to
(a) – 2
(b) 0
(c) 1
(d) 2
Solution:
(cos θ + sin θ)² + (cos θ – sin θ)²
= cos² θ + sin² θ + 2 sin θ cos θ + cos² θ + sin² θ – 2 sin θ cos θ
= 2(sin² θ + cos² θ)
= 2 × 1 = 2 (d)
(∵ sin² θ + cos² θ = 1)

Question 5.
(sec A + tan A) (1 – sin A) is equal to
(a) sec A
(b) sin A
(c) cosec A
(d) cos A
Solution:
(sec A + tan A) (1 – sin A)

Question 6.
\(\frac { { 1+tan }^{ 2 }A }{ { 1+cot }^{ 2 }A } \) is equal to
(a) sec² A
(b) – 1
(c) cot² A
(d) tan² A
Solution:
\(\frac { { 1+tan }^{ 2 }A }{ { 1+cot }^{ 2 }A } \)

Question 7.
If sec θ – tan θ = k, then the value of sec θ + tan θ is
(a) \(1-\frac { 1 }{ k } \)
(b) 1 – k
(c) 1 + k
(d) \(\\ \frac { 1 }{ k } \)
Solution:
sec θ – tan θ = k
\(\frac { 1 }{ cos\theta } -\frac { sin\theta }{ cos\theta } =k\)

Question 8.
Which of the following is true for all values of θ (0° < θ < 90°):
(a) cos² θ – sin² θ = 1
(b) cosec² θ – sec² θ = 1
(c) sec² θ – tan² θ = 1
(d) cot² θ – tan² θ = 1
Solution:
∴ sec² θ – tan² θ = 1 is true for all values of θ as it is an identity.
(0° < θ < 90°) (c)

Question 9.
If θ is an acute angle of a right triangle, then the value of sin θ cos (90° – θ) + cos θ sin (90° – θ) is
(a) 0
(b) 2 sin θ cos θ
(c) 1
(d) 2 sin² θ
Solution:
sin θ cos (90° – θ) + cos θ sin (90° – θ)
= sin θ sin θ + cos θ cos θ
{ ∵ sin(90° – θ) = cosθ, cos (90° – θ) = sin θ }
= sin² θ + cos² θ = 1 (c)

Question 10.
The value of cos 65° sin 25° + sin 65° cos 25° is
(a) 0
(b) 1
(b) 2
(d) 4
Solution:
cos 65° sin 25° + sin 65° cos 25°
= cos (90° – 25°) sin 25° + sin (90° – 25°) cos 25°
= sin 25° . sin 25° + cos 25° . cos 25°
= sin² 25° + cos² 25°
( ∵ sin² θ + cos² θ = 1)
= 1 (b)

Question 11.
The value of 3 tan² 26° – 3 cosec² 64° is
(a) 0
(b) 3
(c) – 3
(d) – 1
Solution:
3 tan² 26° – 3 cosec² 64°
= 3 tan² 26° – 3 cosec (90° – 26°)
= 3 tan² 26° – 3 sec² 26°

Question 12.
The value of \(\frac { sin({ 90 }^{ O }-\theta )sin\theta }{ tan\theta } -1 \) is
(a) – cot θ
(b) – sin² θ
(c) – cos² θ
(d) – cosec² θ
Solution:
\(\frac { sin({ 90 }^{ O }-\theta )sin\theta }{ tan\theta } -1 \)

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS, drop a comment below and we will get back to you at the earliest.