RS Aggarwal Class 7 Solutions Chapter 3 Decimals Ex 3A

RS Aggarwal Class 7 Solutions Chapter 3 Decimals Ex 3A

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 3 Decimals Ex 3A.

Other Exercises

Question 1.
Solution:
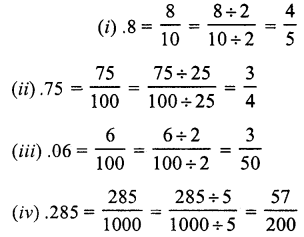
RS Aggarwal Class 7 Solutions Chapter 3 Decimals Ex 3A 1

Question 2.
Solution:
RS Aggarwal Class 7 Solutions Chapter 3 Decimals Ex 3A 2

Question 3.
Solution:
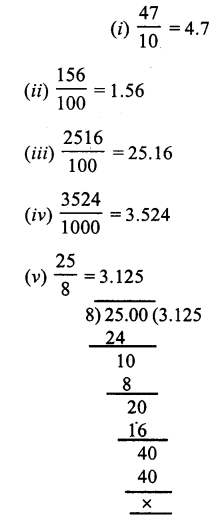
RS Aggarwal Class 7 Solutions Chapter 3 Decimals Ex 3A 3
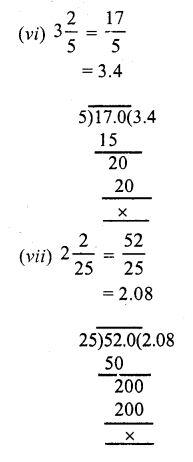
RS Aggarwal Class 7 Solutions Chapter 3 Decimals Ex 3A 4
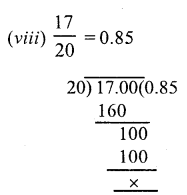
RS Aggarwal Class 7 Solutions Chapter 3 Decimals Ex 3A 5

Question 4.
Solution:
(i) 6.5, 16.03, 0.274, 119.4
In these decimals, the greatest places of decimal is 3
6.5 = 6.500
16.03 = 16.030
0. 274 = 0.274
119.4 = 119.400 are like decimals.
(ii) 3.5, 0.67, 15.6, 4
In these decimal, the greatest place of decimal is 2
3.5 = 3.50
0.67 = 0.67
15.6 = 15.60
4 = 4.00 are the like decimals

Question 5.
Solution:
(i) Among 78.23 and 69.85,
78.23 is greater than 69.85 (78 > 69)
78.23 > 69.85
(ii) Among 3.406 and 3.46,
3.406 is less than 3.46 (40 < 46)
3.406 < 3.46
(iii) Among 5.68 and 5.86,
5.68 is less than 5.86 (68 < 86)
5.68 < 5.86
(iv) Among 14.05 and 14.005
14.5 is greater than 14.005 (05 > 00)
14.5 >14.005
(v) Among 1.85 and 1.805,
1.85 is greater than 1.805 (85 > 80)
1.85 > 1.805
(vi) Among 0.98 and 1.07,
0.98 is less than 1.07 (0 < 1)
0.98 < 1.07

Question 6.
Solution:
(i) 4.6, 7.4, 4.58, 7.32, 4.06
Converting the given decimals into like decimals, we get:
4.60, 7.40, 4.58, 7.32, 4.06.
We see that 4.06 < 4.58 < 4.60 < 7.32 < 7.40.
Writing in ascending order, 4.06, 4.58, 4.6, 7.32, 7.4
(ii) 0.5, 5.5, 5.05, 0.05, 5.55
Converting the given decimals into like decimals, we get:
0. 50, 5.50, 5.05, 0.05, 5.55
We see that 0.05 < 0.50 < 5.05 < 5.50 < 5.55.
Writing in ascending order, 0.05, 0.50, 5.05, 5.5, 5.55
(iii) 6.84, 6.84, 6.8, 6.4, 6.08
Converting the given decimals into like decimals
6.84, 6.48, 6.80, 6.40, 6.08
We see that 6.08 < 6.40 < 6.48 < 6.80 < 6.84
Writing in ascending order,
6.08, 6.4, 6.48, 6.8, 6.84
(iv) 2.2, 2.202, 2.02, 22.2, 2.002
Converting them into like decimals
2.200, 2.202, 2.020, 22.200, 2.002 we see that
2.002 < 2.020 < 2.200 < 2.202 < 22.200
Now writing in ascending order,
2.002, 2.020, 2.2, 2.202, 22.2

Question 7.
Solution:
(i) 7.4, 8.34, 74.4, 7.44, 0.74
Converting them into like decimals,
7.40, 8.34, 74.40, 7.44, 0.74
we see that
74.40 > 8.34 > 7.44 > 7.40 > 0.74
Writing in descending order,
74.4, 8.34, 7.44, 7.4, 0.74
(ii) 2.6, 2.26, 2.06, 2.007, 2.3
Converting them into like decimals,
2.600, 2.260, 2.060, 2.007, 2.300
We see that
2.600 > 2.300 > 2.260 > 2.060 > 2.007
Writing in descending order,
2.6, 2.3, 2.26, 2.06, 2.007

Question 8.
Solution:
RS Aggarwal Class 7 Solutions Chapter 3 Decimals Ex 3A 6

Question 9.
Solution:
RS Aggarwal Class 7 Solutions Chapter 3 Decimals Ex 3A 7

Question 10.
Solution:
RS Aggarwal Class 7 Solutions Chapter 3 Decimals Ex 3A 8

Hope given RS Aggarwal Solutions Class 7 Chapter 3 Decimals Ex 3A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 1 Integers Ex 1A

RS Aggarwal Class 7 Solutions Chapter 1 Integers Ex 1A

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 1 Integers Ex 1A.

Other Exercises

Question 1.
Solution:
(i) 15 + (-8) =15 – 8 = 7
(ii) (-16) +9 = -7
(iii) (-7) + (-23)= -7 – 23 = -30
(iv) (-32) + 47 = -32 + 47 = 15
(v) 53 + (-26) = 53 – 26 = 27
(vi) (-48) + (-36) = -48 – 36 = -84

Question 2.
Solution:
(i) 153 and -302 = 153 + (-302) = 153 – 302 = -149
(ii) 1005 and -277 = 1005 + (-277) = 1005 – 277 = 728
(iii) -2035 and 297 = -2035 + 297 = – 1738
(iv) -489 and -324 = -489 + (-324) = -489 – 324 = -813
(v) -1000 and438 = -1000 + 438 = -562
(vi) -238 and 500 = -238 + 500 = 262

Question 3.
Solution:
Additive inverse of
(i) -83 is – (-83) = 83
(ii) 256 is -256
(iii) 0 is 0
(iv) -2001 is – (-2001) = 2001

Question 4.
Solution:
(i) 28 from – 42 = -42 – (28) = -42 – 28 = -70
(ii) – 36 from 42 = 42 – (-36) = 42 + 36 = 78
(iii) -37 from -53 = -53 – (-37) = -53 + 37= -16
(iv) -66 from -34 = -34 – (-66) = -34 + 66 = 32
(v) 318 from 0 = 0 – (318) = -318
(vi) -153 from -240= -240 – (-153) = -240 + 153 = -87
(vii) -64 from 0 = 0 – (-64) = 0 + 64 = 64
(viii) – 56 from 144 = 144 – (-56) = 144 + 56 = 200

Question 5.
Solution:
– 34 – (-1032 + 878)
= -34 – (-154) = -34 + 154 = 120

Question 6.
Solution:
38 + (-87) – 134
= (38 – 87) – 134
= -49 – 134 = -183

Question 7.
Solution:
(i) {(-13) + 27} + (-41) = (-13) + {27 + (-41)} (By Associative Law of Addition)
(ii) (-26) + {(-49) + (-83)} = {(-26) + (-49)} +(-83) (By Associative Law of Addition)
(iii) 53 + (-37) = (-37) + (53) (By Commutative Law of Addition)
(iv) (-68) + (-76) = (-76) + (-68) (By Commutative Law of Addition)
(v) (-72) + (0) = -72 (Existence of Additive identity)
(vi) -(-83) = 83
(vii) (-60) – (………) = -59 => -60 – (-1) = -59
(viii) (-31) + (……….) = -40 => -31 + (-9) = -40

Question 8.
Solution:
{-13 – (-27)} + {-25 – (-40)}
= {-13 + 27} + {-25 + 40}
= 14 + 15 = 29

Question 9.
Solution:
36 – (- 64) = 36 + 64 = 100
(-64) – 36= -64 – 36 = -100
They are not equal

Question 10.
Solution:
(a + b) + c = {-8 + (-7)} + 6 = (-8 – 7) + 6 = -15 + 6 = -9
and a + (b + c) = -8 + (-7 + 6) = -8 + (-1) = -8 – 1 = -9 Hence proved

Question 11.
Solution:
LHS = (a -b) = -9 – (-6) = -9 + 6 = -3
RHS = (b – a) = -6 – (-9) = -6 + 9 = 3
LHS ≠ RHS.
Hence (a – b) ≠ (b – a)

Question 12.
Solution:
Sum of two integers = -16
One integer = 53
Second integer = -16 – (53) = -16 – 53 = (-69)

Question 13.
Solution:
Sum of two integers = 65
One integer = -31
Second integer = 65 – (-31) = 65 + 31 = 96

Question 14.
Solution:
Difference of a and (-6) = 4
a – (-6) = 4
⇒ a + 6 = 4
⇒ a = 4 – 6
⇒ a = -2

Question 15.
Solution:
(i) We can write any two integers having opposite signs
e.g. 5, -5
Sum = 5 + (-5) = 5 – 5 = 0
(ii) The sum is a negative integer
The greater integer must be negative and smaller integer be positive
e.g. -9, 6
Sum = -9 + 6 = -3
(iii) The sum is smaller than the both integers
Both integer will be negative -4, -6
Sum = -4 + (-6) = -4 – 6 = -10
(iv) The sum is greater than the both integers
Both integers will be positive
e.g. 6, 4
(v) The sum oftwo integers is smaller than one of these integers
The greater number will be positive and smaller be negative
e.g. 6, -4
Sum = 6 + (-4) = 2

Question 16.
Solution:
(i) False: Because, all negative integers are less than zero.
(ii) False: -10 is less than -7.
(iii) Tme: Every negative integer is less than zero.
(iv) True : Sum of two negative integers is negative.
(v) False: It is not always true.

 

Hope given RS Aggarwal Solutions Class 7 Chapter 1 Integers Ex 1A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 1 Integers Ex 1C

RS Aggarwal Class 7 Solutions Chapter 1 Integers Ex 1C

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 1 Integers Ex 1C.

Other Exercises

Question 1.
Solution:
(i) 65 by -13 = 65 ÷ (-13) = -5
(ii) -84 by 12 = -84 ÷ 12 = -7
(iii) -76 by 19 = -76 ÷ 19 = -4
(iv) -132 by 12 = -132 ÷ 12 = -11
(v) -150 by 25 = -150 ÷ 25 = -6
(vi) -72 by -18= -72 ÷ (-18)
(vii) -105 by -21 = -105 ÷ (-21) = 5
(viii) -36 by -1 = -36 ÷ (-1) = 36
(ix) 0 by -31 = 0 ÷ (-31) = 0
(x) -63 by 63 = -63 ÷ 63 = -1
(xi) -23 by -23 = -23 ÷ (-23)
(xii) -8 by 1 = -8 ÷ 1 = -8

Question 2.
Solution:
(i) 72 ÷ (………) = -4
⇒ 72 ÷ (-4) = -18
72 + (-18) = -4
(ii) -36 ÷ (………) = -4
⇒ -36 ÷ (-4) = 9
-36 ÷ (9) = -4
(iii) (………) ÷ (-4) = 24
⇒ -4 x 24 = -96
(-96) ÷ (-4) = 24
(iv) (……….) ÷ 25 = 0
(…….) ÷ 25 = 0 {0 ÷ a = 0}
(v) (………) ÷ (-1) = 36
⇒ 36 x (-1) = -36
(-36) ÷ (-1) = 36
(vi) (………..) + 1 = 37
⇒ (-37) x 1 = -37
(-37) ÷ 1 = -37
(vii) 39 ÷ (……….) = -1
⇒ 39 ÷ (-1) = -39
39 ÷ (-39) = -1
(viii) 1 ÷ (………) = -1
⇒ -1 ÷ 1 = -1
1 ÷ (-1) = -1
(ix) -1 + (………) = -1
-1 ÷ (1) = -1

Question 3.
Solution:
(i) True : as zero divided by non zero integer is zero.
(ii) False : as division by zero is not meaning full
(iii) False : as (-5) ÷ (-1) = 5 (product will be positive)
(iv) True : as -a ÷ 1 = -a
(v) False : as (-1) ÷ (-1) = 1
(vi) True.

Hope given RS Aggarwal Solutions Class 7 Chapter 1 Integers Ex 1C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 7 Solutions Chapter 1 Integers Ex 1B

RS Aggarwal Class 7 Solutions Chapter 1 Integers Ex 1B

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 1 Integers Ex 1B.

Other Exercises

Question 1.
Solution:
(i) 16 by 9 = 16 x 9 = 144
(ii) 18 by -6 = 18 x (-6) = -108
(iii) -36 by -11 = 36 x (-11) = -396
(iv) -28 by 14 = -28 x 14 = -392
(v) -53 by 18 = -53 x 18 = -954
(vi) -35 by 0 = -35 x 0 = 0
(vii) 0 by -23 = 0 x (-23) = 0
(viii) -16 by -12 = (-16) x (-12) = 192
(ix) -105 by -8 = -105 x (-8) = 840
(x) -36 by -50 = (-36) x (-50) = 1800
(xi) -28 by -1 = (-28) x (-1) = 28
(xii) 25 by -11 = 25 x -11 = -275

Question 2.
Solution:
(i) 3 x 4 x (-5) = 12 x (-5) = -60 = 60
(ii) 2 x (-5) x (-6) = (-10) x (-6) = 60
(iii) (-5) x (-8) x (-3) = 40 x (-3) = -120
(iv) (-6) x 6 x (-10) = (-36) x (-10) = 360
(v) 7 x (-8) x 3 =(-56) x 3 = -168
(vi) (-7) x (-3) x 4 = 21 x 4 = 84

Question 3.
Solution:
(i) (-4) x (-5) x (-8) x (-10) = (4 x 5) x (8 x 10)
{Number of negative integers is even}
= 20 x 80 = 1600
(ii) (-6) x (-5) x (-7) x (-2) x (-3)
Here number of negative integers is odd
= (-1) [6 x 5 x 7 x 2 x 3]
= (-1) (1260) = -1260
(iii) (-60) x (-10) x (-5) x (-1)
Here number of negative integers is even
= 60 x 10 x 5 x 1
= 3000
(iv) (-30) x (-20) x (-5)
Here number of negative integers is odd
= (-1) (30 x 20 x 5) = -1 x 3000 = -3000
(v) (-3) x (-3) x (-3) x …6 times
Here number of negative integers is even
= 3 x 3 x 3 x 3 x 3 x 3 = 729
(vi) (-5) x (-5) x (-5) x …5 times
Here number of negative integers is odd
= (-1) (5 x 5 x 5 x 5 x 5)
= (-1) (3125) = – 3125
(vii) (-1) x (-1) x (-1) x …200 times
Here number of negative integers is even
= 1 x 1 x 1 x 1 x 200 times = 1
(viii) (-1) x (-1) x (-1) x …171 times
Here number of negative integers is odd
= (-1) x (1 x 1 x 1 x ……… 171 times)
= -1 x 1 = -1

Question 4.
Solution:
Number of negative integers = 90
which is positive and 9 integers are positive
The sign of the product will be positive

Question 5.
Solution:
Number of negative integers = 103 which is negative
Product will be negative

Question 6.
Solution:
(i) (- 8) x 9 + (- 8) x 7
= (-8) {9 + 7}
= -8 x 16 = -128
(ii) 9 x (-13) + 9 x (-7)
= 9 x (-13 – 7)
= 9 x (-20) = – 180
(iii) 20 x (-16) + 20 x 14 = 20 x {-16 + 14}
= 20 x (-2)= -40
(iv) (-16) x (-15) + (-16) x (-5)
= (-16) x {-15 – 5}
= (-16) x (-20) = 320
(v) (-11) x (-15)+ (-11) x (-25)
-(-11) x {-15 – 25}
= (-11) x (-40) = -440
(vi) 10 x (-12)+ 5 x (-12)
= (-12) {10 + 5} = (-12) x 15 = -180
(vii) (-16) x (-8) + (-4) x (-8)
= (-8){-16 – 4} = (-8) x (-20) = 160
(viii) (-26) x 72 + (-26) x 28
= (-26) (72 + 28) = (-26) x 100 = -2600

Question 7.
Solution:
(i) (-6) x (………) = 6 ⇒ (-6) x (-1) = 6
(ii) (-18) x (………) = (-18) ⇒ (-18) x (1) = (-18)
(iii) (-8) x (-9) = (-9) x (……….) ⇒ (-8) x (-9) = (-9) x (-8) (By Commutative Law of Multiplication)
(iv) 7 x (-3) = (-3) x (……….) ⇒ 7 x (-3) = (-3) x (7) (By Commutative Law of Multiplication)
(v) {(-5) x 3} x (-6) = (………) x {3 x (-6)} ⇒ {(-5) x 3} x (-6) = (-5) x {3 x (-6)} (By Associative Law of Multiplication)
(vi) (-5) x (……….) = 0 ⇒ (-5) x (0) = 0 (By Property of Zero)

Question 8.
Solution:
Number of questions in a test =10
Marks awarded for every correct answer = 5
and marks deducted for every wrong answer = 2 (-2 is given)
(i) Ravi gets 4 correct and 6 incorrect answers
Total marks obtained by him = 4 x 5 – 6 x 2 = 20 – 12 = 8
(ii) Reenu gets 5 correct and 5 incorrect answers
Total marks obtained by her = 5 x 5 – 5 x 2 = 25 – 10= 15
(iii) Heena gets 2 correct and 5 incorrect answers
She gets marks = 2 x 5 – 5 x 2 = 10 – 10 = 0

Question 9.
Solution:
(i) True: As product of a positive and a negative integer is negative.
(ii) False: The product of two negative integers is positive.
(iii) True.
(iv) False: As multiplication of an integer and (-1) is negative.
(v) True as a x b = b x a.
(vi) True as (a x b) x c = a x (b x c)
(vii) False: It is not possible except integer 1.

Hope given RS Aggarwal Solutions Class 7 Chapter 1 Integers Ex 1B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.