RS Aggarwal Class 10 Solutions Chapter 4 Triangles MCQS
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS.
Other Exercises
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself
Choose the correct answer in each of the following questions.
Question 1.
Solution:
(c) A man goes from O to 24 m due west at A and then 10 m due north at B.
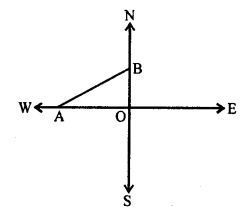
Now, AB² = OA² + OB²
= (24)² + (10)² = 576 + 100 = 676 = (26)²
AB = 26 m
Question 2.
Solution:
(b) Two poles AB and CD are standing on the plane ground 8 m apart.
AB = 13 m and CD = 7 m, CE || DB
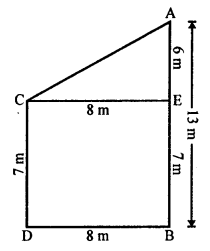
In right ∆ACE,
AC² = CE² + AE²
= (8)² + (6)² = 64 + 36 = 100 = (10)²
AC = 10 m
Distance between the tops of poles = 10 m
Question 3.
Solution:
(c) A vertical stick AB = 1.8 m
and its shadow = 45 cm = 0.45 m
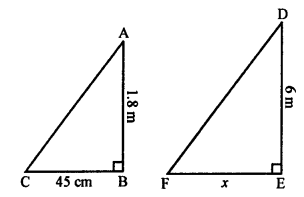
At the same time, let x cm be the shadow of 6 m long pole.
∆ABC ~ ∆DEF
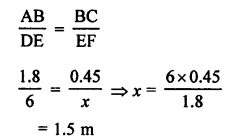
Question 4.
Solution:
(d) Shadow of a vertical pole 6 m long is 3.6 m on the ground and shadow of a tower at the same, is 18 m.
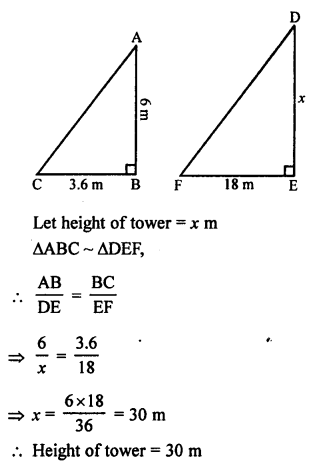
Question 5.
Solution:
(d) Shadow of 5 m long stick = 2 m
Let shadow of 12.5 m high tree at the same time = x
∆ABC ~ ∆DEF
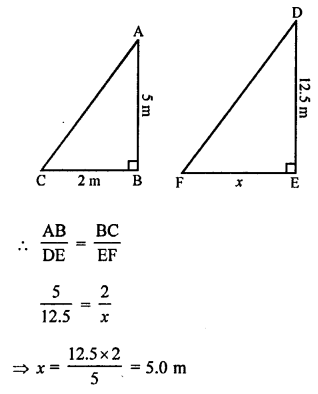
Question 6.
Solution:
(a) Length of ladder AB = 25 m .
Height above the ground = 24 m
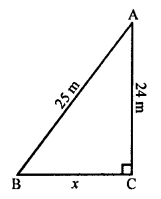
Let its foot is x m away from the foot of building.
In right ∆ABC,
AB² = AC² + BC² (Pythagoras Theorem)
(25)² = (24)² + x²
⇒ 625 = 576 + x²
⇒ x² = 625 – 576 = 49 = (7)²
x = 7
Distance = 7 m
Question 7.
Solution:
(b) O is a point inside ∆MNP such that
MOP = 90°, OM = 16 cm, OP = 12 cm.
If MN = 21 cm ∠NMP = 90°, then NP = ?
Let MP = x Now, in right ∆MOP,
∠O = 90°
MP² = OM² + OP² (Pythagoras Theorem)
= (16)² + (12)² = 256 + 144 = 400 = (20)²
MP = 20 cm
Now, in right ∆MNP, ∠M = 90°
NP² = MN² + MP²
= (21)² + (20)² = 441 + 400 = 841 = (29)²
NP = 29 cm
Question 8.
Solution:
(b) Let ∆ABC is a right angled triangle with ∠B = 90°
AC = 25 cm
Let one side AB of the other two sides = x cm
then second side BC = (x + 5) cm
According to the Pythagoras Theorem,
AC² = AB² + BC²
(25)² = x² + (x + 5)²
625 = x² + x² + 10x + 25
⇒ 2x² + 10x + 25 – 625 = 0
⇒ 2x² + 10x – 600 = 0
⇒ x² + 5x – 300 = 0
⇒ x² + 20x – 15x – 300 = 0
⇒ x (x + 20) – 15 (x + 20) = 0
⇒ (x + 20)(x – 15) = 0
Either x + 20 = 0, then x = -20 which is not possible being negative,
or x – 15 = 0, then x = 15
First side = 15 cm
and second side = 15 + 5 = 20 cm
Question 9.
Solution:
(b) Side of an equilateral triangle = 12 cm
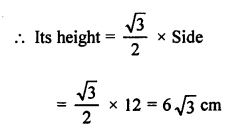
Question 10.
Solution:
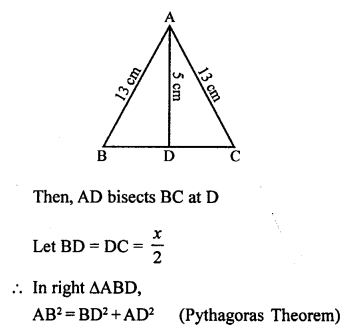
(d) In isosceles ∆ABC,
AB = AC = 13 cm
Length of altitude AB, (from A to BC) = 5 cm
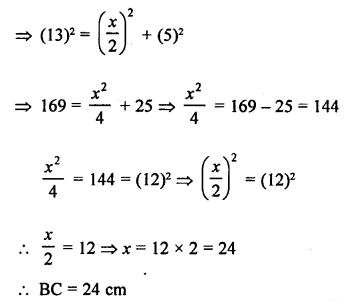
Question 11.
Solution:
(a) In the given figure,
AB = 6 cm, AC = 8 cm
AD is the bisector of ∠A which meets BC at D.
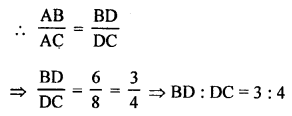
Question 12.
Solution:
(d) In the given figure,
AD is the internal bisector of ∠A
BD = 4 cm, DC = 5 cm, AB = 6 cm
Let AC = x cm
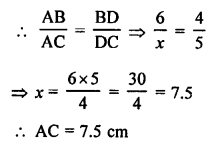
Question 13.
Solution:
(b) In the given figure,
AD is the bisector of ∠A of ∆ABC.
AB = 10 cm, AC = 14 cm and BC = 6 cm
Let CD = x cm
Then BD = (6 – x) cm
Now, AD is the bisector of ∠A
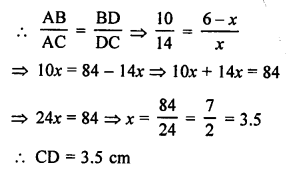
Question 14.
Solution:
(b) In a ∆ABC, AD ⊥ BC and BD = DC
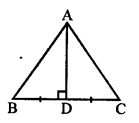
In a ∆ABC, AD = \(\frac { 1 }{ 2 }\) BC and BD = DC.
In right ∆ABD and ∆ACD
AD = AD (common)
∠ABD = ∠ADC (each 90°)
BD = DC (given)
∆ABD = ∆ACD (SAS axiom)
AB = AC
∆ABC is an isosceles triangle.
Question 15.
Solution:
(c) In equilateral ∆ABC, AD ⊥ BC
Then BD = DC = \(\frac { 1 }{ 2 }\) BC
Now, in right ∆ABD,
AB² = BD² + AD² (Pythagoras Theorem)

Question 16.
Solution:
(c) In a rhombus, each side = 10 cm and one diagonal = 12 cm
AB = BC = CD = DA = 10 cm BD = 12 cm
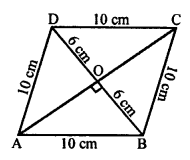
The diagonals of a rhombus bisect each other at right angles.
In ∆AOB,
AB² = AO² + BO²
⇒ (10)² = AO² + (6)²
⇒ AO² = (10)² – (6)² = 100 – 36 = 64 = 8²
AO = 8 cm
Diagonals AC = 2 x AO = 2 x 8 = 16 cm
Question 17.
Solution:
(b) Length of diagonals of a rhombus are 24 cm and 10 cm.
The diagonals of a rhombus bisect each other at right angles.
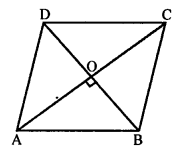
In rhombus ABCD
AO = OC, BO = OD
Let AO = OC = \(\frac { 24 }{ 2 }\) = 12 cm
BO = OD = \(\frac { 10 }{ 2 }\) = 5 cm
Now, in right ∆AOB,
AB² = AO² + BO² (Pythagoras Theorem)
= (12)² + (5)² = 144 + 25 = 169 = (13)²
AB = 13
Each side of rhombus = 13 cm
Question 18.
Solution:
(b) Diagonals of e. quadrilateral divides each other proportionally, then it is
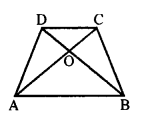
In quadrilateral ABCD, diagonals AC and BD intersect each-other at O and \(\frac { AO }{ OC }\) = \(\frac { BO }{ OD }\)
Then, quadrilateral ABCD is a trapezium.
Question 19.
Solution:
(a) In the given figure,
ABCD is a trape∠ium and its diagonals AC
and BD intersect at O.
and OA = (3x – 1) cm OB = (2x + 1) cm, OC and OD = (6x – 5) cm

Question 20.
Solution:
(a) The line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram
Question 21.
Solution:
(c) If the bisector of angle of a triangle bisects the opposite side of a triangle.
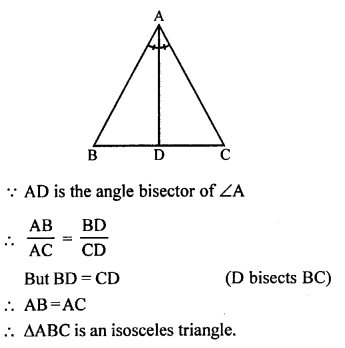
Question 22.
Solution:
(a) In ∆ABC,
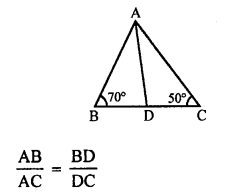
∠B = 70° and ∠C = 50°
But ∠A + ∠B + ∠C = 180° (Angles of a triangle)
∠A = 180° – (∠B + ∠C)
= 180° – (70° + 50°)
= 180° – 120° = 60°
\(\frac { AB }{ AC }\) = \(\frac { BD }{ DC }\)
AD is the bisector of ∠A
∠BAD = \(\frac { 60 }{ 2 }\) = 30°
Question 23.
Solution:
(b) In ∆ABC, DE || BC
AD = 2.4 cm, AE = 3.2 cm, EC = 4.8 cm
Let AD = x cm
DE || BC
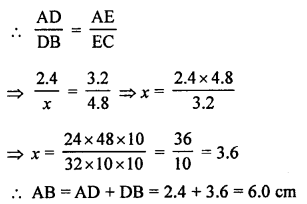
Question 24.
Solution:
(b) In ∆ABC, DE || BC
AB = 7.2 cm, AC = 6.4 cm, AD = 4.5 cm
Let AE = x cm
DE || BC
∆ADE ~ ∆ABC
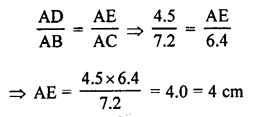
Question 25.
Solution:
(c) In ∆ABC, DE || BC
AD = (7x – 4) cm, AE = (5x – 2) cm DB = (3x + 4) cm and EC = 3x cm
In ∆ABC, DE || BC
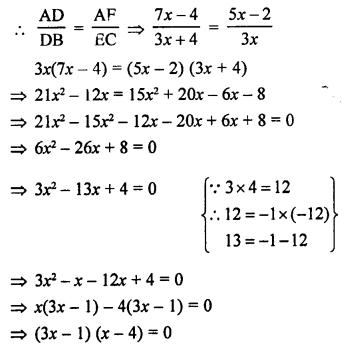
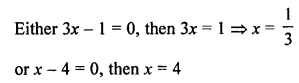
Question 26.
Solution:
(d) In ∆ABC, DE || BC
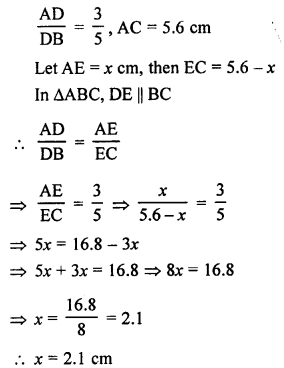
Question 27.
Solution:
(b) ∆ABC ~ ∆DEF
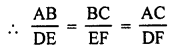

Question 28.
Solution:
(a) ∆ABC ~ ∆DEF

Question 29.
Solution:
(d) ∆DEF ~ ∆ABC

Perimeter of ∆DEF = DE + EF + DF
= 12 + 8 + 10 = 30 cm
Question 30.
Solution:
(d) ABC and BDE are two equilateral triangles such that D is the midpoint of BC.
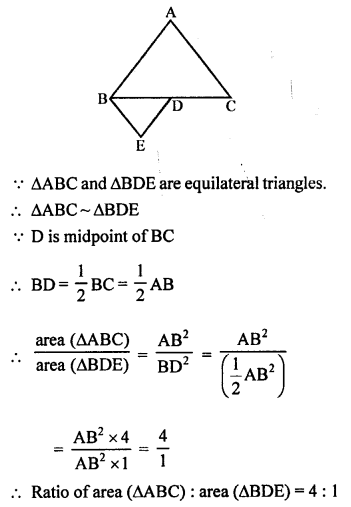
Question 31.
Solution:
(b) ∆ABC ~ ∆DFE.
∠A = 30°, ∠C = 50°, AB = 5cm, AC = 8 cm and DF = 7.5 cm
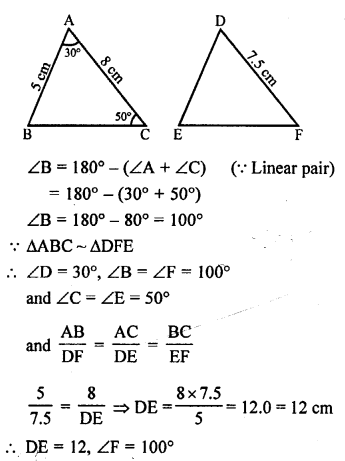
Question 32.
Solution:
(c) In ∆ABC, ∠A = 90°
AD ⊥ BC
In ∆ABD and ∆ADC

Question 33.
Solution:
(c) In ∆ABC, AB = 6 cm, AC = 12 cm and BC = 6 cm.
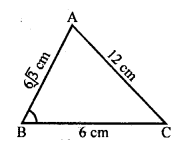
Longest side (AC)2 = (12)2 = 144
AB2 + BC2 = (6√3)2 + (6)2 = 108 + 36 = 144
AC2 = AB2 + BC2 (Converse of Pythagoras Theorem)
∠B = 90°
Question 34.
Solution:
(c) In ∆ABC and ∆DEF, \(\frac { AB }{ DE }\) = \(\frac { BC }{ FD }\)
For similarity,
Here, included angles must be equal and these
are ∠B = ∠D.
Question 35.
Solution:
(b) In ∆DEF and ∆PQR,
∠D = ∠Q and ∠R = ∠E
Question 36.
Solution:
(c) ∆ABC ~ ∆EDF
∠A = ∠E, ∠B = ∠D, ∠C = ∠F
Question 37.
Solution:
(b) In ∆ABC and ∆DEF,
∠B = ∠E, ∠F = ∠C and AB = 3DE
The triangles are similar as two angles are equal but including sides are not proportional.
Question 38.
Solution:
(a)

Question 39.
Solution:
(d) In the given figure, two line segments AC and BD intersect each other at P such that
PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°
In ∆ABP and ∆CPD,

Question 40.
Solution:
(d) Corresponding sides of two similar triangles = 4:9
The areas of there triangle will be in the ratio
Question 41.
Solution:
(d)
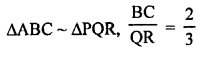
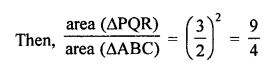
Question 42.
Solution:
(b) In the given figure,
∆ABC is an equilateral triangle.
D is midpoint of AB and E is the midpoint of AC.
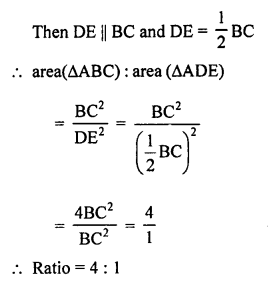
Question 43.
Solution:
(b)
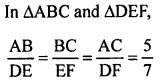
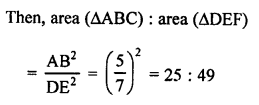
Question 44.
Solution:
(b) ∆ABC ~ ∆DEF
ar (∆ABC) = 36 cm² and ar (∆DEF) = 49 cm²
i.e. areas are in the ratio 36 : 49
Ratio in their corresponding sides = √36 : √49 = 6 : 7
Question 45.
Solution:
(c) Two isosceles triangles have their corresponding angles equal and ratio in their areas is 25 : 36.
The ratio in their corresponding altitude
(heights) = √25 : √36 = 5 : 6 (∆s are similar)
Question 46.
Solution:
(b) The line segments joining the midpoints of a triangle form 4 triangles which are similar to the given (original) triangle.
Question 47.
Solution:
(b) ∆ABC ~ ∆QRP
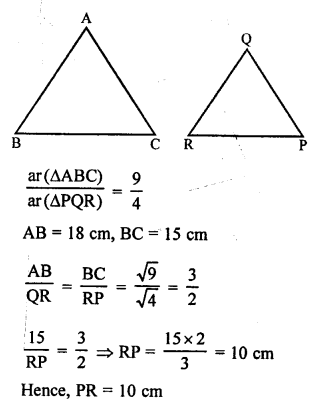
Question 48.
Solution:
(c) In the given figure, O is the point of intersection of two chords AB and CD.
OB = OD and ∠AOC = 45°
∠B = ∠D (Angles opposite to equal sides)
∠A = ∠D, ∠C = ∠B (Angles in the same segment)
and ∠AOC = ∠BOD = 45° each
∆OAC ~ ∆ODB (AAA axiom)
OA = OC (Sides opposite to equal angles)
∆OAC and ∆ODB are isosceles and similar.
Question 49.
Solution:
(d) In an isosceles ∆ABC,
AC = BC
⇒ AB² = 2 AC²
⇒ AB² = AC² + AC²
⇒ AB² = AC² + BC² (AC = BC)
Converse of the Pythagoras Theorem,
∆ABC is a right triangle and angle opposite to AB = 90°
∠C = 90°
Question 50.
Solution:
(b) In ∆ABC,
AB = 16 cm, BC = 12 cm and AC = 20 cm
(Longest side)2 = 20² = 400
Sum of square on other sides = AB² + BC²
= 162 + 122 = 256 + 144 = 400
AC² = AB² + BC²
∆ABC is a right triangle.
True/False type
Question 51.
Solution:
(c) (a) False. Not always congruent.
(b) False. Two similar figures are similar if they have same shape, not size in every case.
(c) True.
(d) False. Not in each case.
Question 52.
Solution:
(a) True
(b) False, as ratio of the areas of the two similar triangles is equal to the ratio of the square of their corresponding sides.
(c) True
(d) True
Question 53.
Matching of columns : (2 marks)
Solution:




Question 54.
Solution:


correct answer is
(a) → (r)
(b) → (q)
(c) → (p)
(d) → (s)
Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.