RS Aggarwal Class 10 Solutions Chapter 4 Triangles Test Yourself
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself.
Other Exercises
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
- RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself
MCQ
Question 1.
Solution:
(b) ∆ABC ~ ∆DEF
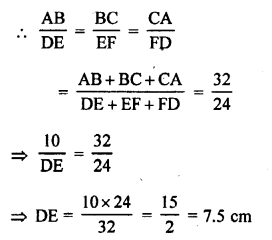
Question 2.
Solution:
(a) In the given figure,
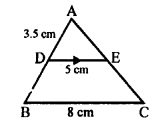

Question 3.
Solution:
(b) Length of pole AB = 6 m
and CD = 11 m
and distance between the BD = 12 m
Draw AE || BD, then
ED = AB = 6 m, AE = BD = 12 m
CE = CD – ED = 11 – 6 = 5 m
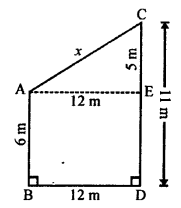
Now, in right ∆ACE,
AC² = AE² + CE² (Pythagoras Theorem)
= (12)² + (5)² = 144 + 25 = 169 = 13²
AC = 13
Distance between their tops = 13 m
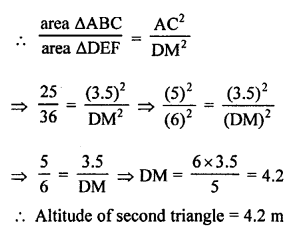
Question 4.
Solution:
(c) Area of two similar triangles ABC and DEF are 25 cm² and 36 cm².
Altitude of first ∆ABC is AL = 3.5 m.
Let DM be the altitude of second triangle.
Short-Answer Questions
Question 5.
Solution:
∆ABC ~ ∆DEF
and 2AB = DE
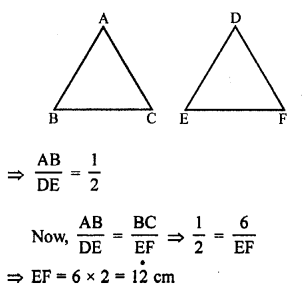
Question 6.
Solution:
In the given figure,
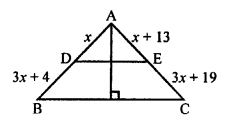
DE || BC, AL ⊥ BC
AD = x cm,
DB = (3x + 4) cm AE = (x + 3) cm, EC = (3x + 19) cm
In ∆ABC, DE || BC
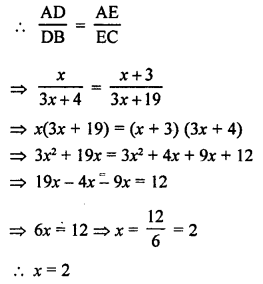
Question 7.
Solution:
Let AB be the ladder, and A is the window.
Length of ladder AB = 10 m and AC = 8 m
Distance between the foot of the ladder from the house = x m
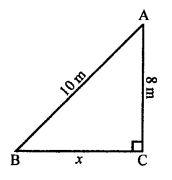
In right ∆ABC,
AB² = AC² + BC²
⇒ (10)² = (8)² + (x)²
⇒x² = (10)² – (8)²
⇒ x² = 100 – 64 = 36
⇒ x² = (6)²
⇒ x = 6
Distance between the foot of ladder and foot of the house = 6m.
Question 8.
Solution:
In ∆ABC, AB = BC = CA = 2a cm
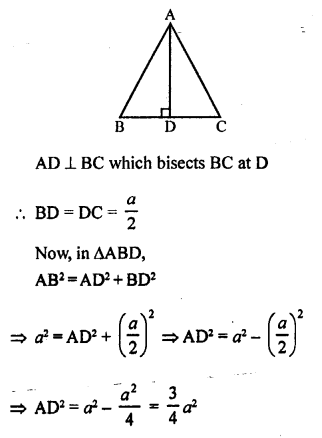
AD ⊥ BC which bisects the base BC at D
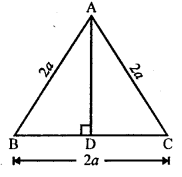
BD = DC = \(\frac { 2a }{ 2 }\) = a cm
Now, in right ∆ABD
AB² = AD² + BD²
(2a)² = AD² + a²
⇒ AD² = 4a² – a² = 3a²
AD = √3a² = √3 a
Height of altitude = √3 a cm
Question 9.
Solution:
Let EF = x cm
∆ABC ~ ∆DEF
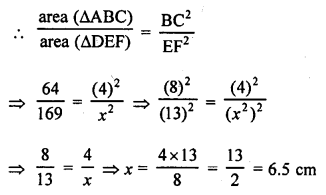
Question 10.
Solution:
ABCD is a trape∠ium in which AB || DC
AB = 2CD
Diagonals AC and BD intersect each other at O.
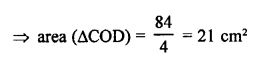
Question 11.
Solution:
Let corresponding sides of two similar triangles ABC and DEF are in the ratio 2 : 3.
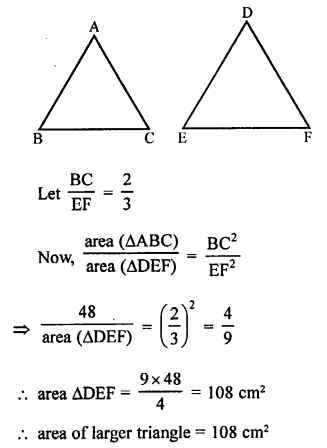
Question 12.
Solution:
In the given figure,
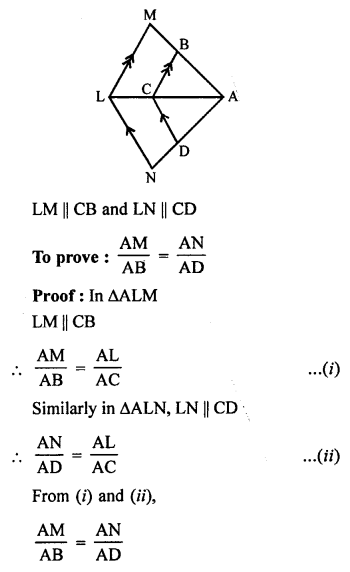
Question 13.
Solution:
Given : In ∆ABC, AD is the bisector of ∠A which meets BC at D.
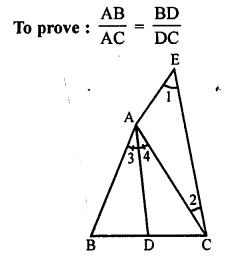
Construction : Produce BA and draw CE || DA meeting BA produced at E.
DA || CE
∠3 = ∠1 (corresponding angles)
∠4 = ∠2 (alternate angles)
But ∠3 = ∠4 (AD is the bisector of ∠A)
∠1 = ∠2
AC = AE (Sides opposite to equal angles)
Now, in ∆AEC,
AD || EC
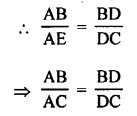
Question 14.
Solution:
Given : In ∆ABC,
AB = BC = CA = a cm
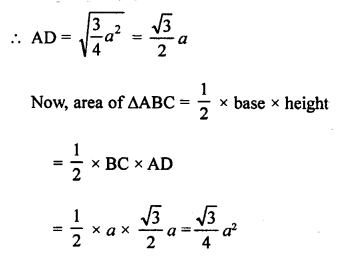
Question 15.
Solution:
In rhombus ABCD, diagonals AC = 24 cm and BD = 10 cm.
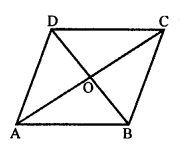
The diagonals of a rhombus bisect each other at right angles.
AO = OC = \(\frac { 24 }{ 2 }\) = 12 cm
and BO = OD = \(\frac { 10 }{ 2 }\) = 5 cm
Now, in right ∆AOB,
AB² = AO² + BO² = 12² + 5² = 144 + 25 = 169 = (13)²
AB = 13
Each side of a rhombus = 13 cm
Question 16.
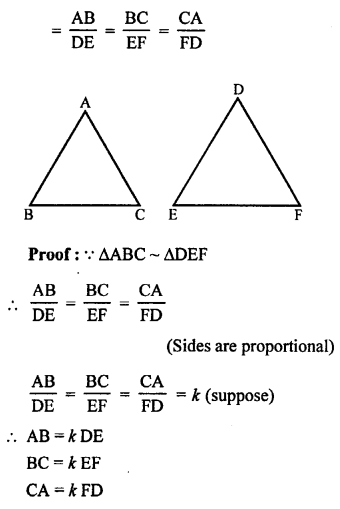
Solution:
Given : ∆ABC ~ ∆DEF

Long-Answer Questions
Question 17.
Solution:
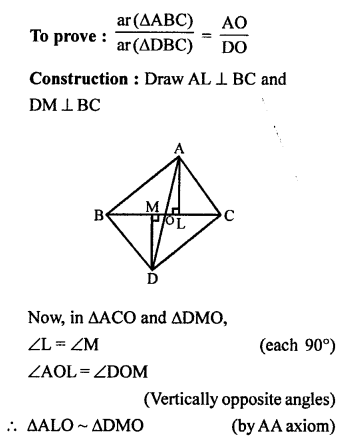
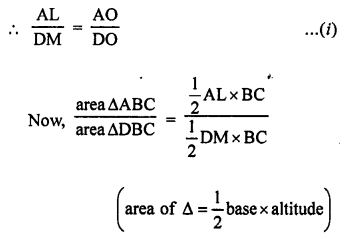
Given: In the given figure, ∆ABC and ∆DBC are on the same base BC but in opposite sides.
AD and BC intersect at O.

Question 18.
Solution:
In the given figure,
XY || AC and XY divides
∆ABC into two regions equal in area

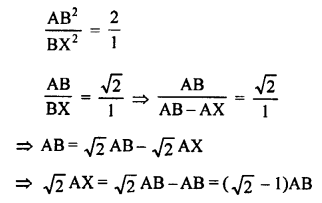
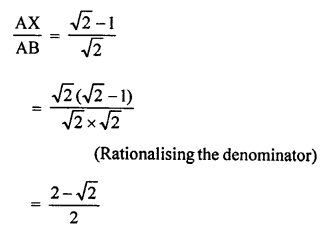
Question 19.
Solution:
In the given figure, ∆ABC is an obtuse triangle, obtuse angle at B.
AD ⊥ CB produced.
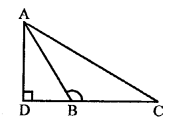
To prove : AC² = AB² + BC² + 2BC x BD
Proof: In ∆ADB, ∠D = 90°
AB² = AD² + DB² (Pythagoras Theorem)
⇒ AD² = AB² – DB² ……(i)
Similarly, in right ∆ADC,
AC² = AD² + DC²
= AB² – DB² + (DB + BC)² [From (i)]
= AB² – DB² + DB² + BC² + 2BC x BD
= AB² + BC² + 2 BC x BD
Question 20.
Solution:
In the given figure,
PA, QB and RC is perpendicular to AC.
AP = x, QB = z, RC =y, AB = a and BC = b.

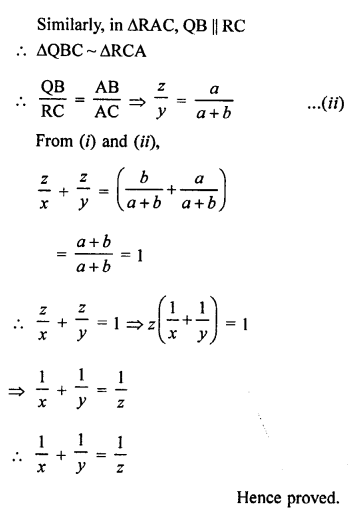
Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.