RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4A

RS Aggarwal Class 10 Solutions Chapter 4 Triangles Ex 4A

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4B
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4C
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4D
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4E
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles MCQS
• RS Aggarwal Solutions Class 10 Chapter 4 Triangles Test Yourself

Question 1.
Solution:
In ∆ABC, points D and E are on the sides AB and AC respectively such that DE || BC.



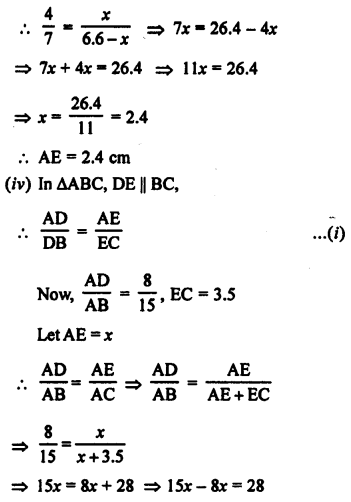
⇒ 7x = 28 ⇒ x = 4

Question 2.
Solution:
D and E are the points on the sides AB and AC of ∆ABC respectively and DE || BC,


By cross multiplication,
⇒ (7x – 4) (3x) = (5x – 2) (3x + 4)
⇒ 21x² – 12x = 15x² + 20x – 6x – 8
⇒ 21x² – 12x – 15x² – 20x + 6x = -8
⇒ 6x² – 26x + 8 = 0
⇒ 3x² – 13x + 4 = 0
⇒ 3x² – 12x – x + 4 = 0
⇒ 3x (x – 4) – 1 (x – 4) = 0
⇒ (x – 4) (3x – 1) = 0
Either x – 4 = 0, then x = 4
or 3x – 1 = 0 then 3x = 1 ⇒ x = \(\frac { 1 }{ 3 }\) which is not possible
x = 4

Question 3.
Solution:
D and E are the points on the sides AB and AC of ∆ABC
(i) AD = 5.7 cm, DB = 9.5 cm, AE = 4.8 cm and EC = 8 cm

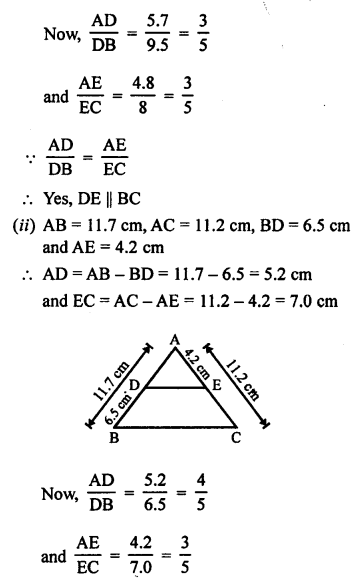
Question 4.
Solution:
In ∆ABC, AD is the bisector of ∠A

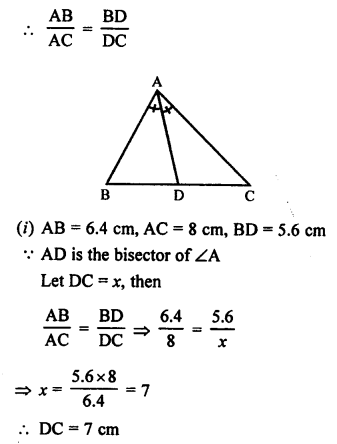
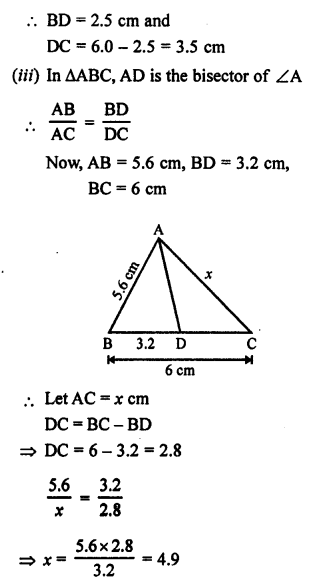
Question 5.
Solution:
Given : M is a point on the side BC of a parallelogram ABCD.
DM when produced meets AB produced at N.

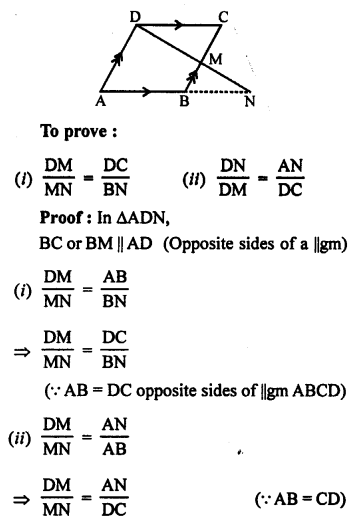
Question 6.
Solution:
Given : In trapezium AB || DC.
M and N are the mid points of sides AD and BC respectively.
MN is joined.
To prove : MN || AB or DC.
Construction: Produce AD and BC to meet at P.

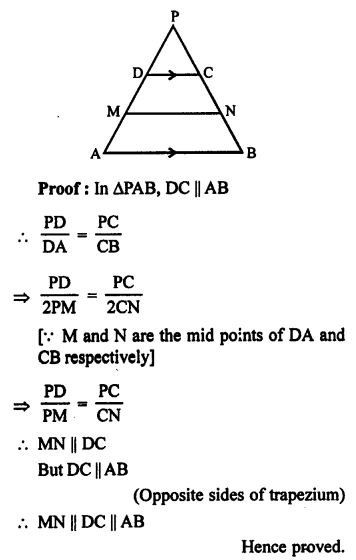
Question 7.
Solution:
ABCD is a trapezium and its diagonals AC and BD intersect each other at O.

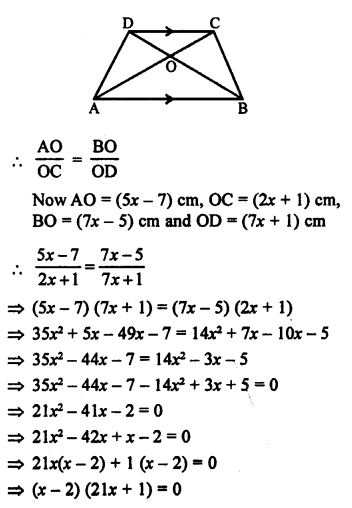
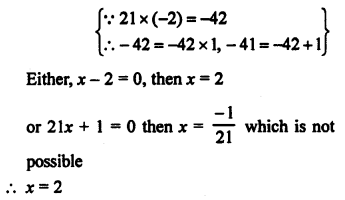
Question 8.
Solution:
Given : In ∆ABC, M and N are points on the sides AB and AC respectively such that
BM = CN and if ∠B = ∠C.

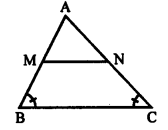
Question 9.
Solution:
Given : ∆ABC and ∆DBC are on the same side of BC.
P is any point on BC.
PQ || AB and PR || BD are drawn, which meet AC at Q and CD at R.
AD is joined.
To prove : QR || AD.
Proof:
In ∆ABC, PQ||AB


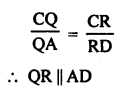
Hence proved.

Question 10.
Solution:
Given : In the given figure, D is the mid point of BC. AD is joined. O is any point on AD. BO and CO are produced to meet AC at F and AB at E respectively. AD is produced to X such that D is the mid point of OX.
To prove: AO : AX = AF : AB and EF || BC
Construction. Join BX and CX.

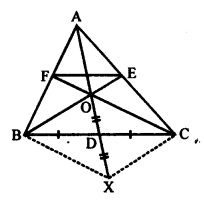
D is the midpoint of BC.
Proof: BD = DC and OD = DX. (given)
OBXC is a parallelogram. (Diagonals of a ||gm bisect each other)

Question 11.
Solution:
Given : In ||gm, ABCD, P is mid point of DC and Q is the mid point of AC. Such that
CQ = \(\frac { 1 }{ 4 }\) AC.
PQ is produced to meet BC at R.
To prove : R is the mid point of BC.
Construction : Join BD which intersects AC at O.

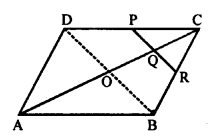
Proof: Diagonals of a parallelogram bisect each other
CO = \(\frac { 1 }{ 2 }\) AC.
But CQ = \(\frac { 1 }{ 2 }\) CO (given)
Q is the mid point of CO.
PQ || DO
⇒ PR || DB and P is mid point of CD
R is the midpoint BC.
Hence proved.

Question 12.
Solution:
Given : In ∆ABC, AB = AC
D and E are the points on AB and AC such that
AD = AE
To prove : BCED is a cyclic quadrilateral.
Proof: In ∆ABC,
AB = AC,
D and E are the mid points of AB and AC respectively.

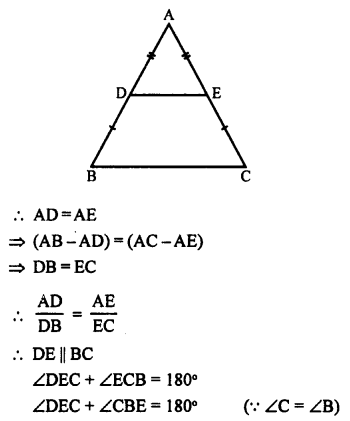
But these are opposite angles of quad. BCED
BCED is a cyclic quadrilateral
Hence, B, C, E and D are concyclic.

Question 13.
Solution:
Given : In ∆ABC, BD is the bisector of AB which meets AC at D.
A line PQ || AC which meets AB, BC, BD at P, Q, R respectively.
To prove : PR x BQ = QR x BP
Proof: In ∆ABC, PQ || AC
and BD is the bisector of ∠B

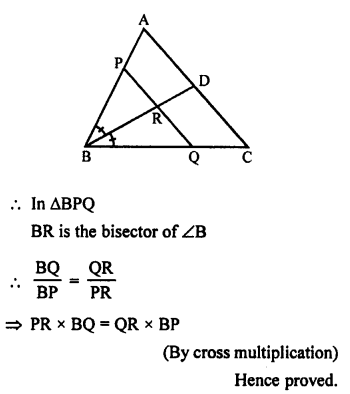
Hope given RS Aggarwal Solutions Class 10 Chapter 4 Triangles Ex 4A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.