RS Aggarwal Class 9 Solutions Chapter 13 Volume and Surface Area Ex 13C
These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Class 9 Solutions Chapter 13 Volume and Surface Area Ex 13C.
Other Exercises
- RS Aggarwal Solutions Class 9 Chapter 13 Volume and Surface Area Ex 13A
- RS Aggarwal Solutions Class 9 Chapter 13 Volume and Surface Area Ex 13B
- RS Aggarwal Solutions Class 9 Chapter 13 Volume and Surface Area Ex 13C
- RS Aggarwal Solutions Class 9 Chapter 13 Volume and Surface Area Ex 13D
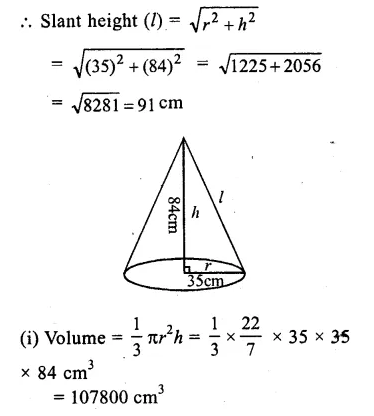
Question 1.
Solution:
Radius of base (r) = 35cm
and height (h) = 84cm.

Question 2.
Solution:
Height of cone (h) = 6cm
Slant height (l) = 10cm.
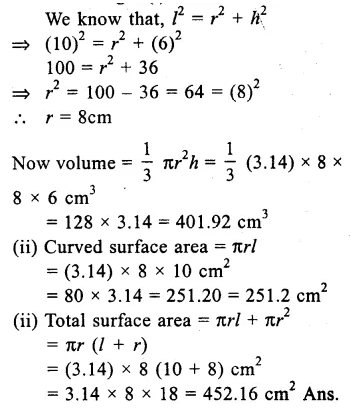
Question 3.
Solution:
Volume of right circular cone = (100 π) cm3
Height (h) = 12cm.
Let r be the radius of the cone
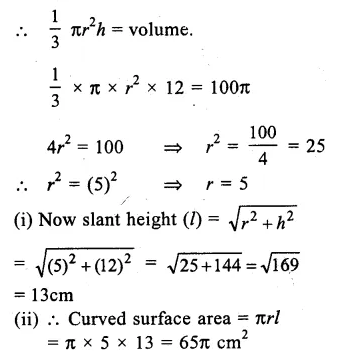
Question 4.
Solution:
Circumference of the base = 44cm

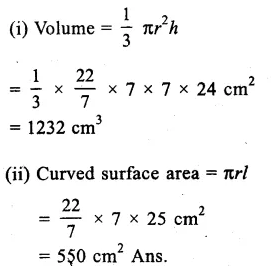
Question 5.
Solution:
Slant height of the cone (l) = 25cm
Curved surface area = 550 cm2
Let r be the radius
πrl = curved surface area
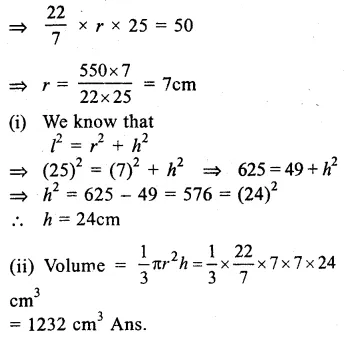
Question 6.
Solution:
Radius.of base (r) = 35cm.
Slant height (l) = 37cm.
We know that
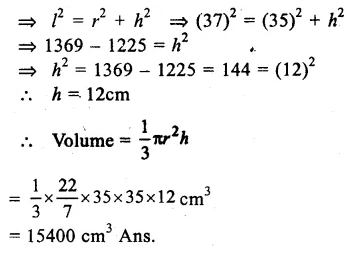
Question 7.
Solution:
Curved surface area = 4070 cm2
Diameter of the base = 70cm

Question 8.
Solution:
Radius of the conical tent = 7m
and height = 24 m.

Question 9.
Solution:
Radius of the first cone (r) = 1.6 cm.
and height (h) = 3.6 cm.

Question 10.
Solution:
Ratio in their heights =1:3
and ratio in their radii = 3:1
Let h1,h2 he their height and r1,r2 be their radii, then
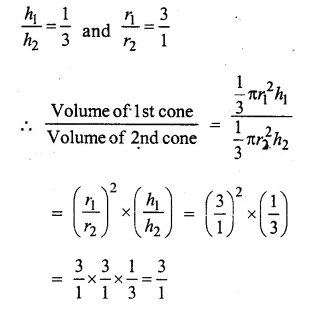
The ratio between their volumes is 3:1
hence proved
Question 11.
Solution:
Diameter of the tent = 105m
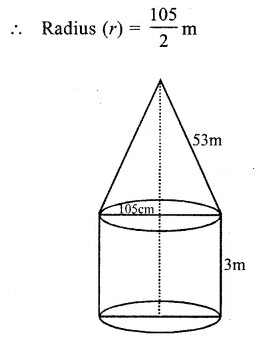

Question 12.
Solution:
No. of persons to be s accommodated =11
Area to be required for each person = 4m2
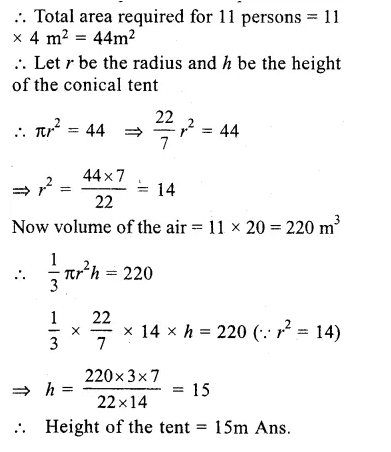
Question 13.
Solution:
Height of the cylindrical bucket (h) = 32cm
Radius (r) = 18cm
Volume of sand filled in it = πr2h
= π x 18 x 18 x 32 cm3
= 10368π cm3
Volume of conical sand = 10368 π cm3
Height of cone = 24 cm

Question 14.
Solution:
Let h be the height and r be the radius of the cylinder and cone.
Curved surface area of cylinder = 2πrh
and curved surface area of cone = πrl
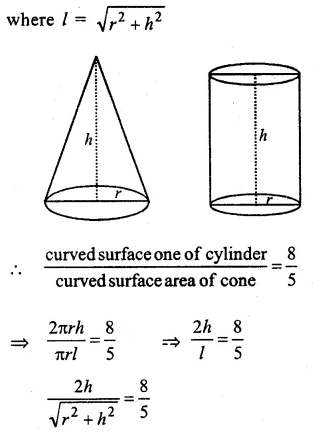

Question 15.
Solution:
Diameter of the pillar = 20cm
Radius (r) = \(\frac { 20 }{ 2 } \) = 10cm
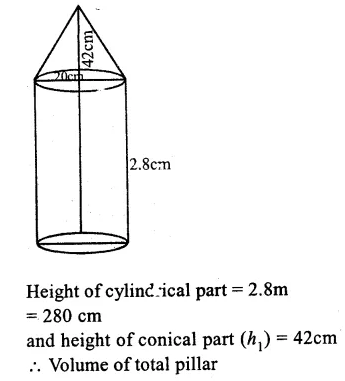
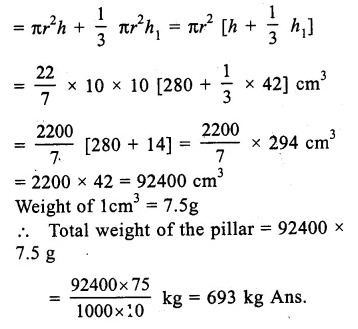
Question 16.
Solution:
Height of the bigger cone (H) = 30cm
By cutting a small cone from it, then volume of smaller cone = \(\frac { 1 }{ 27 } \) of volume of big cone
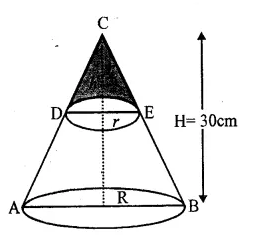
Let radius and height of the smaller cone be r and h
and radius and height of the bigger cone be R and H.
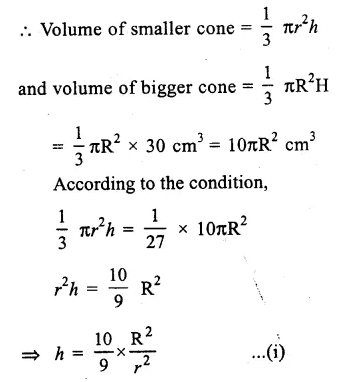
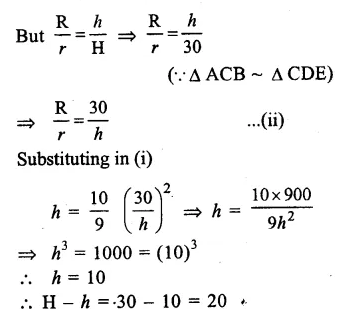
Hence at the height of 20cm from the base it was cut off. Ans.
Question 17.
Solution:
Height of the cylinder (h) = 10cm.
Radius (r) = 6cm.
Height of the cone = 10cm
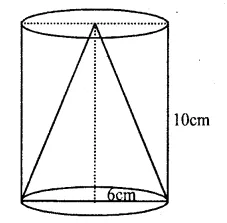
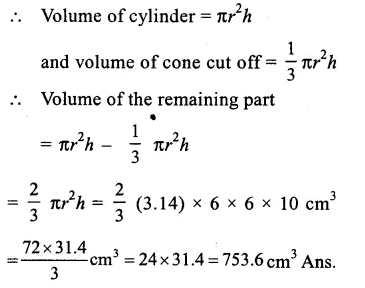
Question 18.
Solution:
Diameter of conical vessel = 40cm
Radius (r) = \(\frac { 40 }{ 2 } \) = 20cm
and depth (h) = 24cm.
.’. Volume = \(\frac { 1 }{ 3 } \) πr2h


Hope given RS Aggarwal Class 9 Solutions Chapter 13 Volume and Surface Area Ex 13C are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.