RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1C

RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1C

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1C.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1A
• RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1B
• RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1C
• RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1D
• RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1E
• RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1F
• RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1G
• RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1H

Question 1.
Solution:
(i) \(\\ \frac { -2 }{ 5 } \) + \(\\ \frac { 4 }{ 5 } \)
= \(\\ \frac { -2+4 }{ 5 } \) = \(\\ \frac { 2 }{ 5 } \)

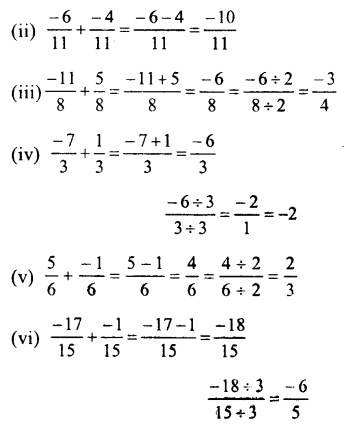
Question 2.
Solution:
(i) \(\frac { 3 }{ 4 } +\left( \frac { -3 }{ 5 } \right) \)
\(\frac { 15+\left( -12 \right) }{ 20 } =\frac { 15-12 }{ 20 } =\frac { 3 }{ 20 } \)

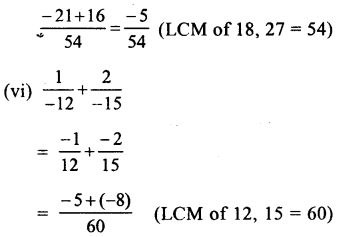
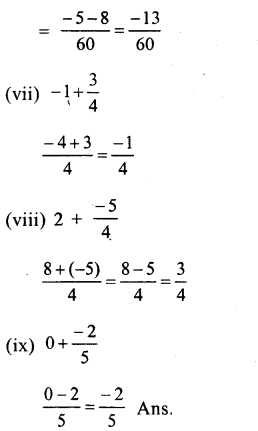
Question 3.
Solution:
(i) L.H.S = \(\\ \frac { -12 }{ 5 } \) + \(\\ \frac { 2 }{ 7 } \)
= \(\\ \frac { -84+10 }{ 35 } \) = \(\\ \frac { -74 }{ 35 } \)

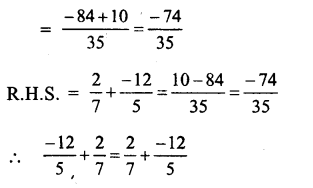
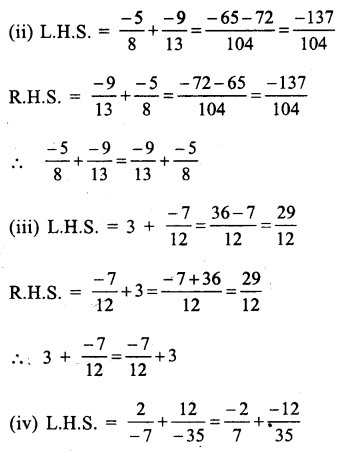
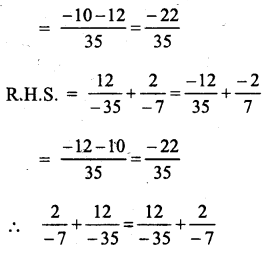
Question 4.
Solution:

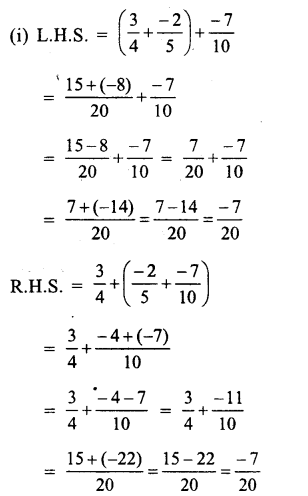
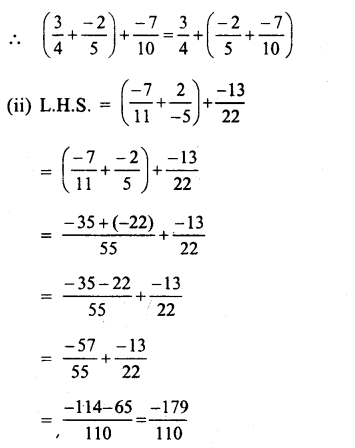
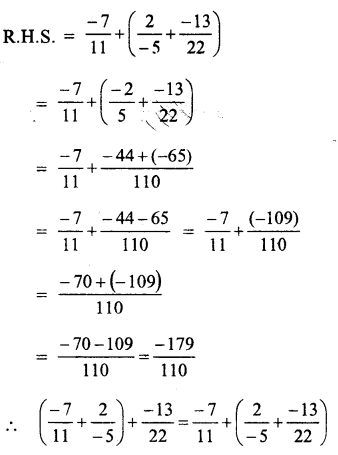
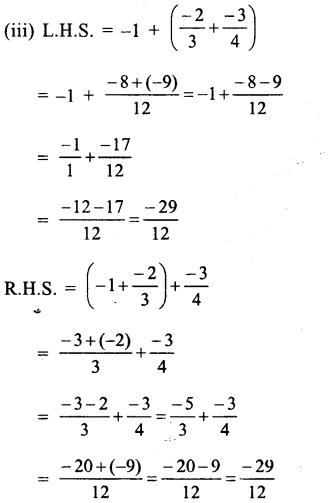
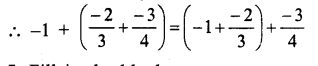
Question 5.
Solution:

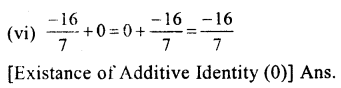
Question 6.
Solution:
We know that additive inverse of \(\\ \frac { a }{ b } \) is \(\\ \frac { -a }{ b } \) and of \(\\ \frac { -a }{ b } \) is \(\\ \frac { a }{ b } \).
Therefore Additive inverse of

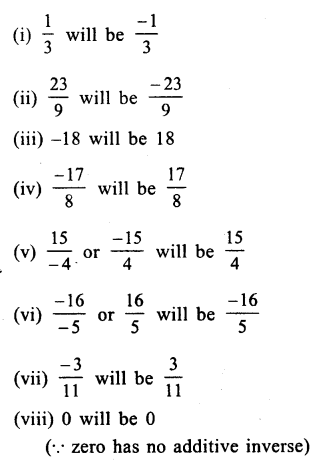
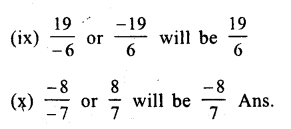
Question 7.
Solution:
(i) \(\\ \frac { 3 }{ 4 } \) from \(\\ \frac { 1 }{ 3 } \) or \(\\ \frac { 1 }{ 3 } \) – \(\\ \frac { 3 }{ 4 } \)
= \(\\ \frac { 4-9 }{ 12 } \) = \(\\ \frac { -5 }{ 12 } \)

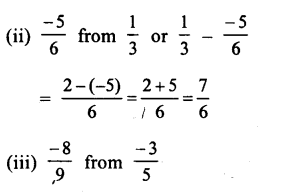
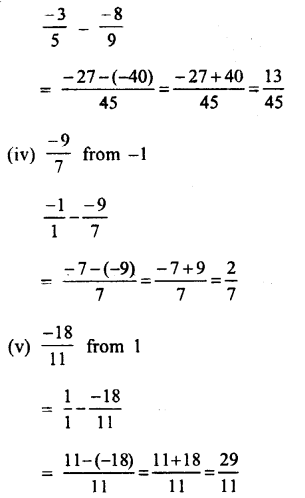
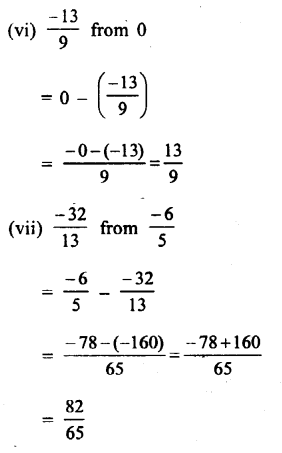
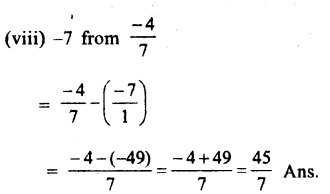
Question 8.
Solution:

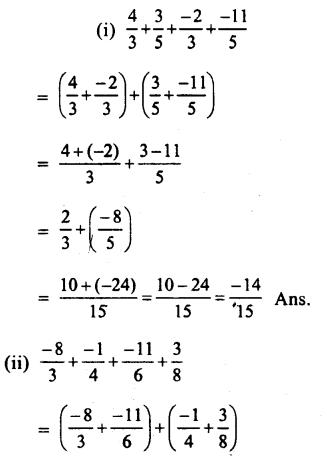
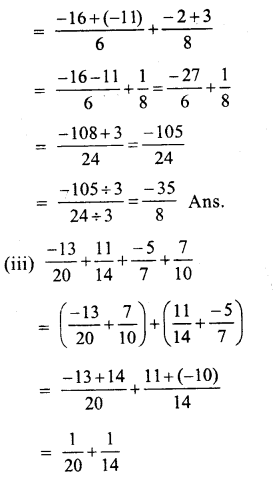
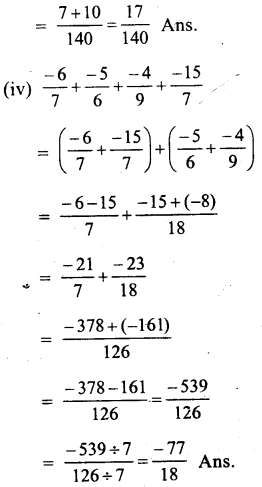
Question 9.
Solution:
Sum of two numbers = – 2
one number = \(\\ \frac { -14 }{ 5 } \)

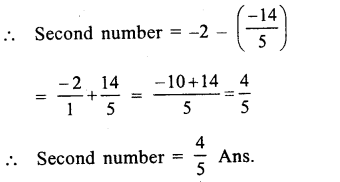
Question 10.
Solution:
Sum of two numbers = \(\\ \frac { -1 }{ 2 } \)
One number = \(\\ \frac { 5 }{ 6 } \)

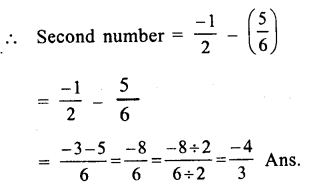
Question 11.
Solution:
Sum of two numbers = \(\\ \frac { -3 }{ 2 } \)
one number = \(\\ \frac { -5 }{ 8 } \)

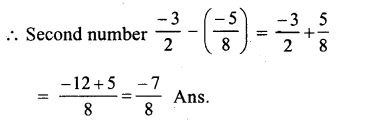
Question 12.
Solution:
Sum of two numbers = \(\\ \frac { 5 }{ 7 } \)
One number = – 1
Second number = \(\\ \frac { 5 }{ 7 } \) – ( – 1)
= \(\\ \frac { 5 }{ 7 } \) + \(\\ \frac { 1 }{ 1 } \)
\(\\ \frac { 5+7 }{ 7 } \) = \(\\ \frac { 12 }{ 7 } \)

Question 13.
Solution:
Difference of two numbers = \(\\ \frac { -1 }{ 6 } \)
One number = \(\\ \frac { -2 }{ 3 } \)

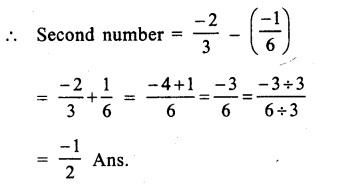
Question 14.
Solution:
(i) 0 is the rational number.
(ii) Yes, the difference of two rational numbers is also rational.
(iii) Yes, addition is commutative.
(iv) Yes, addition associative.
(v) No, subtraction is not commutative.
(vi) No, subtraction is not associative.
(vii) The number itself.

Hope given RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.