RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1A

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1A.

Other Exercises

Question 1.
Solution:
(i) 20 = 5 x 4
\(\\ \frac { -3 }{ 5 } \) = \(\\ \frac { -3X4 }{ 5X4 } \)
(multiplying numerator and denominator by 4)
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1A 1

You can also Download NCERT Solutions for Class 8 Maths to help you to revise complete Syllabus and score more marks in your examinations.

Question 2.
Solution:
98 = 7 x 14
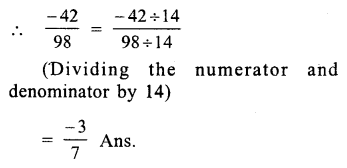
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1A 3

Question 3.
Solution:
60 = 5 x 12
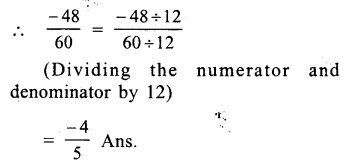
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1A 4

Question 4.
Solution:
(i) \(\\ \frac { -12 }{ 30 } \)
H.C.F of 12 and 30 = 6
Dividing the numerator and denominator
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1A 5

Question 5.
Solution:
(i) \(\\ \frac { 3 }{ 8 } \) or 0
We know that every positive rational number is greater than 0.
∴\(\\ \frac { 3 }{ 8 } \) is greater
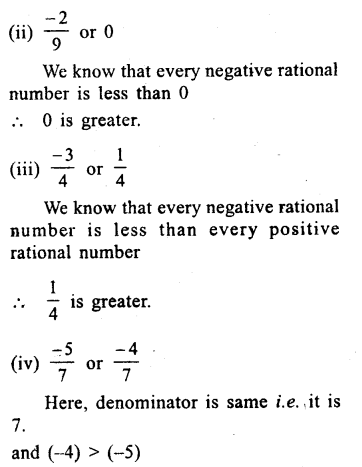
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1A 7

and clearly \(\frac{-1}{2} \) is greater. Ans.

Question 6.
Solution:
(i) \(\\ \frac { -4 }{ 3 } \) or \(\\ \frac { 8 }{ 7 } \)
Her,denominator are not same
LCM of 3 and 7 = 21
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1A 10

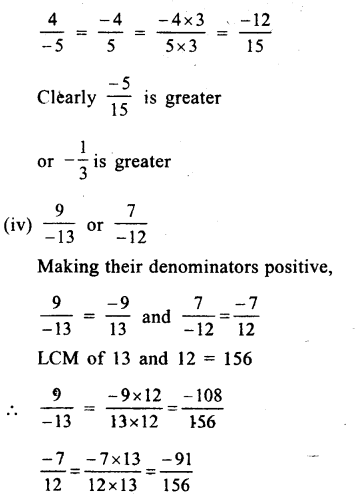
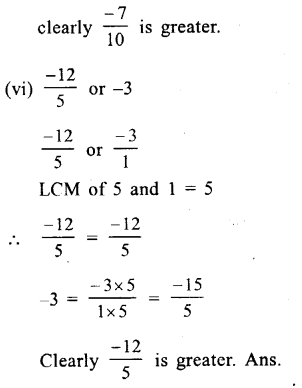
Question 7.
Solution:
(i) Between \(\\ \frac { -3 }{ 7 } \) and \(\\ \frac { 6 }{ -13 } \)
or \(\\ \frac { -3 }{ 7 } \) and \(\\ \frac { -6 }{ 13 } \)
LCM of 7 and 13 = 91
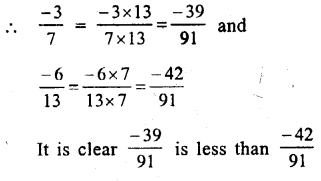
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1A 15

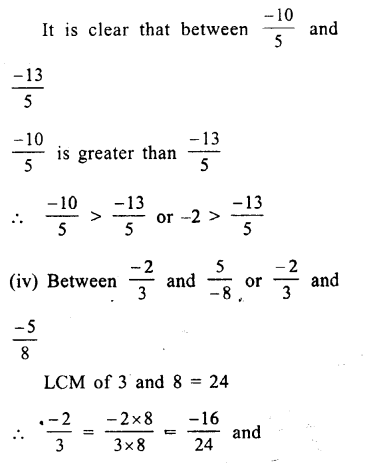
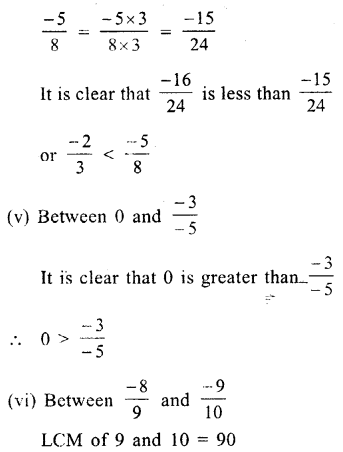
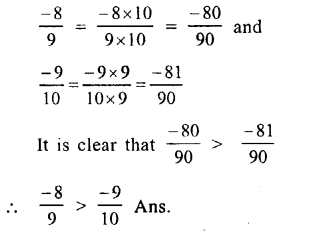
Question 8.
Solution:
Among, \(\\ \frac { 4 }{ -9 } \),\(\\ \frac { -5 }{ 12 } \),\(\\ \frac { 7 }{ -18 } \),\(\\ \frac { -2 }{ 3 } \) making their denominator positive,we get:
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1A 20

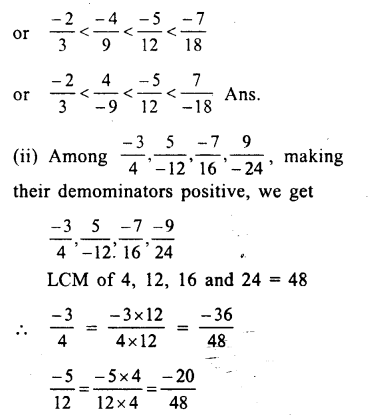
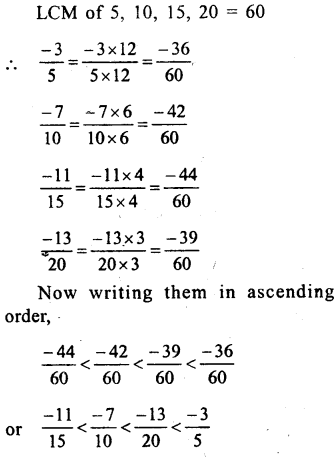
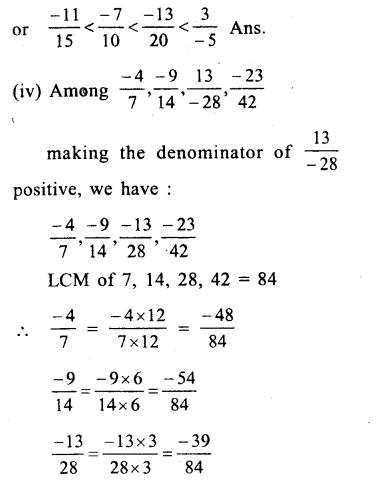
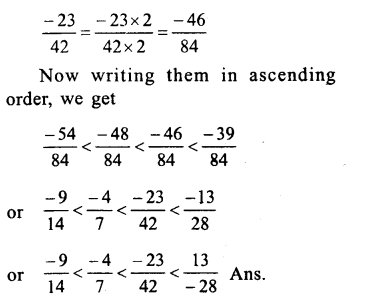
Question 9.
Solution:
(i)Among – 2,\(\\ \frac { -13 }{ 6 } \),\(\\ \frac { 8 }{ -3 } \),\(\\ \frac { 1 }{ 3 } \)
Making the denominator of \(\\ \frac { 8 }{ -3 } \) as
RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1A 26

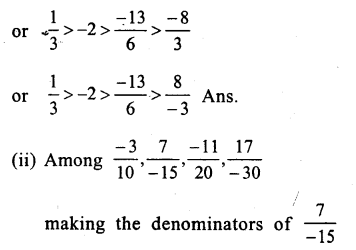
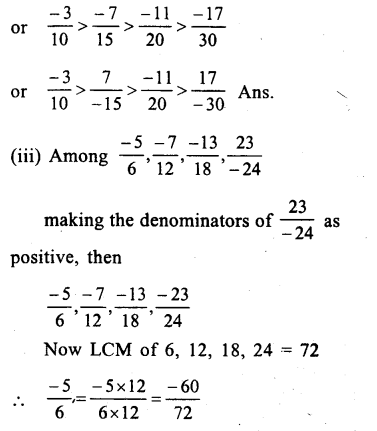
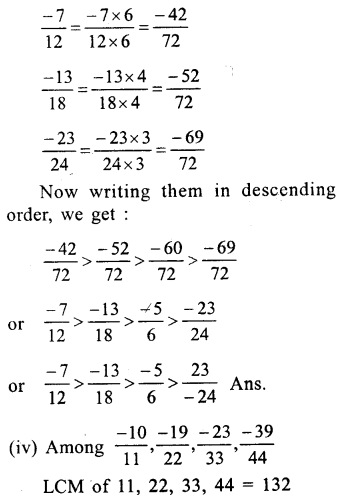
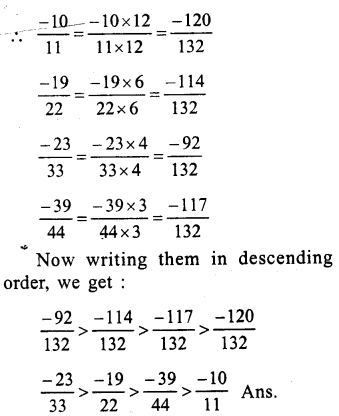
Question 10.
Solution:
(i) True, as the set of whole numbers is a subset of the set of rational numbers
(ii) True, as the set of integers is a subset of the set of rational numbers.
(iii) False, as 0 is a whole number and set of the whole number is a subset of rational numbers
∴ 0 is also a rational number.

Hope given RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.