RS Aggarwal Class 8 Solutions Chapter 1 Rational Numbers Ex 1H
These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1H.
Other Exercises
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1A
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1B
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1C
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1D
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1E
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1F
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1G
- RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1H
Objective Questions :
Tick the correct answer in each of the following :
Question 1.
Solution:
Answer = (c)
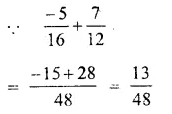
Question 2.
Solution:
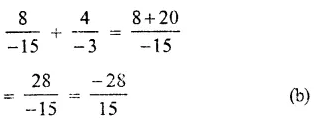
Question 3.
Solution:

Question 4.
Solution:
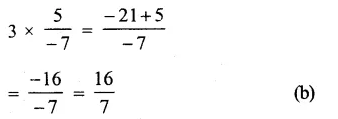
Question 5.
Solution:
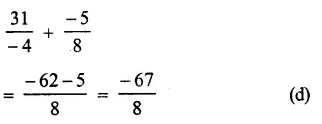
Question 6.
Solution:
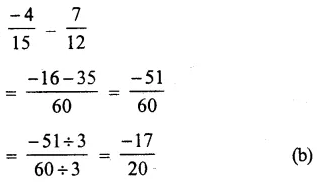
Question 7.
Solution:
Answer = (b)
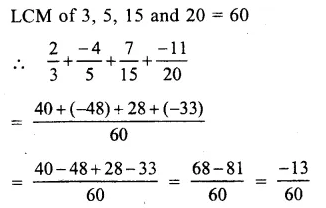
Question 8.
Solution:
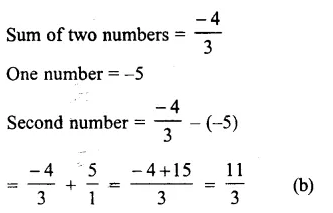
Question 9.
Solution:
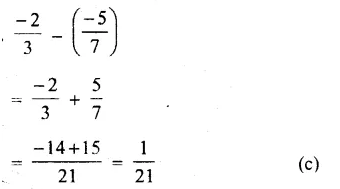
Question 10.
Solution:
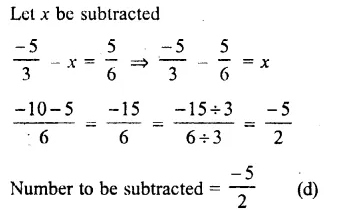
Question 11.
Solution:
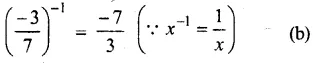
Question 12.
Solution:
Product of two numbers = \(\\ \frac { -28 }{ 81 } \)
One number = \(\\ \frac { 14 }{ 27 } \)
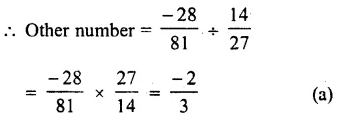
Question 13.
Solution:
Answer = (c)
Let x be the required number, then
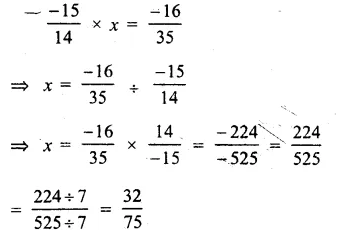
Question 14.
Solution:
Answer = (d)
Let x is to be subtracted then
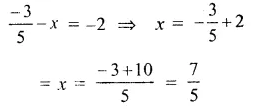
Question 15.
Solution:
Answer = (c)
sum = -3,one number = \(\\ \frac { -10 }{ 3 } \)
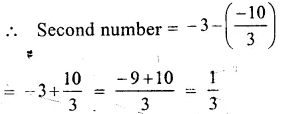
Question 16.
Solution:
Answer = (c)
We know that a number is called in standard form if the numerator and denominator has no common divisor except 1.
\(\\ \frac { -9 }{ 6 } \) is in standard form.
Question 17.
Solution:
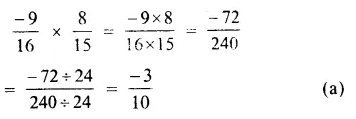
Question 18.
Solution:
Answer = (b)
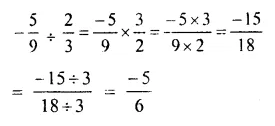
Question 19.
Solution:
Answer = (d)
Let x is required rational
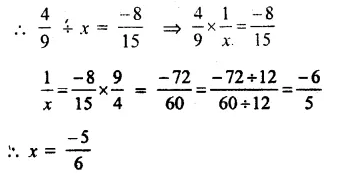
Question 20.
Solution:
Additive inverse of \(\\ \frac { -5 }{ 9 } \) is = – \(\left( \frac { -5 }{ 9 } \right) \)
Question 21.
Solution:
Reciprocal of \(\\ \frac { -3 }{ 4 } \) is \(\\ \frac { -4 }{ 3 } \)
Question 22.
Solution:
A rational number between = \(\\ \frac { -2 }{ 3 } \)
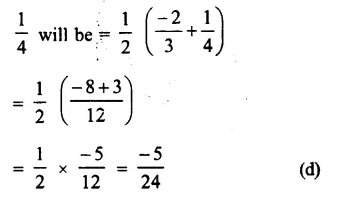
Question 23.
Solution:
Answer: (b)
The reciprocal of a negative rational
the number is also a negative rational number.
Hope given RS Aggarwal Solutions Class 8 Chapter 1 Rational Numbers Ex 1H are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.