RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A

RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12A

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 12 Circles Ex 12A.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 12 Circles Ex 12A
• RS Aggarwal Solutions Class 10 Chapter 12 Circles Ex 12B
• RS Aggarwal Solutions Class 10 Chapter 12 Circles MCQS
• RS Aggarwal Solutions Class 10 Chapter 12 Circles Test Yourself

Question 1.
Solution:
PT is the tangent to the circle with centre O and radius OT = 20 cm.
P is a point 29 cm away from O.

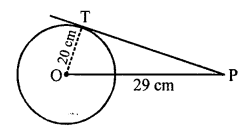
OP = 29 cm, OT = 20 cm
OT is radius and PT is the tangent
OT ⊥ PT
Now, in right ∆OPT,
OP² = OT² + PT² (Pythagoras Theorem)
⇒ (29)² = (20)² + PT²
⇒ 841 = 400 + PT²
⇒ PT² = 841 – 400
⇒ PT² = 441 = (21)²
⇒ PT = 21
Length of tangent PT = 21 cm

Question 2.
Solution:
P is a point outside the circle with centre O and OP = 25 cm
PT is the tangent to the circle and OT is the radius

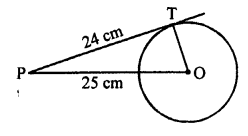
OT ⊥ PT
PT = 24 cm
Now, in right ∆OPT,
OP² = OT² + PT² (Pythagoras Theorem)
⇒ 25² = OT² + (24)²
⇒ 625 = OT² + 576
⇒ OT² = 625 – 576 = 49 = (7)²
OT = 7 cm
or radius of the circle is 7 cm.

Question 3.
Solution:
Given : Two concentric circles with centre O and radii 6.5 cm and 2.5 cm respectively.
AB is a chord of the larger circle which touches the smaller circle at C.

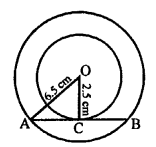
To find : The length of AB.
Join OC, OA.
AB is tangent to the smaller circle and OC is the radius.
OC ⊥ AB and OC bisects AB at C.
AC = CB
OA = 6.5 cm, OC = 2.5 cm
Now, in right ∆OAC,
OA² = OC² + AC² (Pythagoras Theorem)
6.5² = 2.5² + AC²
⇒ 42.25 = 6.25 + AC²
⇒ AC² = 42.25 – 6.25 = 36 = (6)²
⇒ AC = 6
Length of chord AB = 2 x AC = 2 x 6 = 12 cm

Question 4.
Solution:
Given : In the given figure, a circle is inscribed in a triangle ABC which touches the sides AB, BC, CA at D, E and F respectively.
AB = 12 cm, BC = 8 cm and AC = 10 cm.

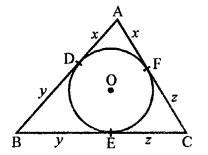
To find : Lengths of AD, BE and CF.
AD and AF are tangents to the circle from A.
AD = AF = x.
Similarly, BD and BE are tangents to the circle.
BD = BE = y
and CE and CF are tangents to the circle
CE = CF = z
x + y + 12 …(i)
y + z = 8 …(ii)
z + x = 10 …(iii)
Adding, 2(x + y + z) = 12 + 8 + 10 = 30
x + y + z = 15 …(iv)
Now, subtracting (ii), (iii) and (i) respectively from (iv)
x = 15 – 8 = 7
y = 15 – 10 = 5
z = 15 – 12 = 3
AD = 7 cm, BE = 5 cm and CF = 3 cm

Question 5.
Solution:
Given : In the given figure,
PA and PB are the tangents drawn from P to the circle with centre O.
OA and OB are joined.
To prove : A, O, B and P are concyclic.
Proof : PA is tangent and OA is the radius.
OA ⊥ PA
∠OAP = 90° …(i)
Similarly, OB is the radius and PB is the tangent
OB ⊥ PB
∠OBP = 90° …(ii)
Adding (i) and (ii)
∠OAP + ∠OBP = 90° + 90° = 180°
But these are the opposite angles of the quadrilateral AOBP
Quadrilateral AOBP is a cyclic
Hence A, O, B and P are concylic

Question 6.
Solution:
Given : In the given figure, chord AB of larger circle of the two concentric circles with centre O, touches the smaller circle at C.
To prove : AC = CB.
Construction : Join OC, OA and OB.

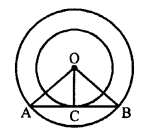
Proof: AB is tangent to the smaller circles and OC is the radius.
OC ⊥ AB.
In right ∆OAC and ∆OBC,
Hypotenuse OA = OB (radii of the same circle)
Side OC = OC (common)
∆OAC = ∆OBC (RHS axiom)
AC = CB (c.p.c.t.)

Question 7.
Solution:
Given : In the figure, from an external point P of the circle, PA and PB are tangents to the circle with centre O.
CD is a tangent at E.
PA = 14 cm.
To find : Perimeter of ∆PCD.
Proof: PA and PB are tangents from P to the circle.
PA = PB …(i)
CA and CE are tangents to the circle.
CA = CE …(ii)
Similarly,
DB = DE
Now, perimeter of ∆PCD
= PC + CD + PD
= PC + CE + ED + PD
= PC + CA + BD + PD
= PA + PB [From (i) and (ii)]
= 14 + 14 = 28 cm

Question 8.
Solution:
A circle with centre O, is inscribed in a ∆ABC touching it at P, Q, R respectively
AB = 10 cm, AR = 7 cm and CR = 5 cm

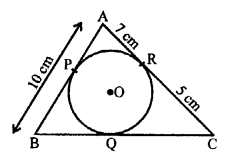
To find, the length of BC
AP and AR are the tangents to the circle
AP = AR = 7 cm
BP = AB – AP = 10 – 7 = 3 cm
BP and BQ are the tangents to the circle
BQ = BP = 3 cm
Similarly, CQ = CR = 5 cm
BC = BQ + CQ = 3 + 5 = 8 cm

Question 9.
Solution:
In the figure, a circle with centre O, touches the sides of a quadrilateral ABCD at P, Q, R and S respectively.

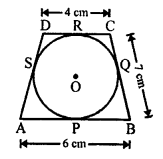
AB = 6 cm, BC = 7 cm and CD = 4 cm
To find, the length of AD.
We know that tangents from an external point to a circle are equal.
AP = AS, BP = BQ
CR = CQ and DR = DS
Now, AP + BP + CR + DR = AS + BQ + CQ + DC
⇒ (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
⇒ AD = (AB + CD) – BC = (6 + 4 – 7) = 3 cm (AB = 6 cm, CD = 4 cm and BC = 7 cm)
Hence, AD = 3 cm.

Question 10.
Solution:
In the given figure, an isosceles ∆ABC in which AB = AC, is circumscribed a circle.
The circle touches its sides BC, CA and AB at P, Q and R respectively.
To prove : P bisects the base BC.
i.e. BP = PC
Proof : AR and AQ are tangents to the circle.
AR = AQ But AB = AC
AB – AR = AC – AQ
⇒ BR = CQ …(i)
BR and BP are tangents to the circle.
BR = BP …(ii)
Similarly,
CP and CQ are tangents
CP = CQ …(iii)
BR = CQ (proved)
From (ii) and (iii),
BP = CP or BP = PC
Hence, P is midpoint of BC.

Question 11.
Solution:
In the given figure, O is the centre of two concentric circles with radii 4 cm and 6 cm respectively.
PA and PB are the tangents drawn from P, to the outer circle and inner circle respectively.
PA = 10 cm

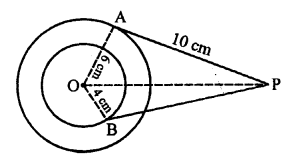
To find, the length of PB (upto one place of decimal)
OA and OB are the radii and PA and PB are two tangents to the circles respectively
OA ⊥ PA and OB ⊥ PB
In right ∆OAP,
OP² = OA² + PA² (Pythagoras Theorem)
= (6)² + (10)² = 36 + 100 = 136
Similarly, in right ∆OBP,
OP² = OB² + PB²
136 = (4)² + PB²
⇒ 136 = 16 + PB²
⇒ PB² = 136 – 16 = 120
PB = √120 cm = 2√30 cm = 2 x 5.47 = 10.94 = 10.9 cm

Question 12.
Solution:
In the given figure, ∆ABC circumscribed the circle with centre O.
Radius OD = 3 cm
BD = 6 cm, DC = 9 cm
Area of ∆ABC = 54 cm²
To find : Lengths of AB and AC.
Construction : Join OA, OB, OC, OE and OF.

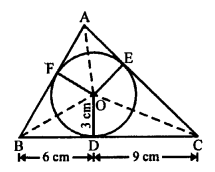
Proof : OE = OF = OD = 3 cm, radii of the same circle.
BD and BF are tangents to the circle.
BD = BF = 6 cm
Similarly, CD = CE = 9 cm and AE = AF = x (Suppose)

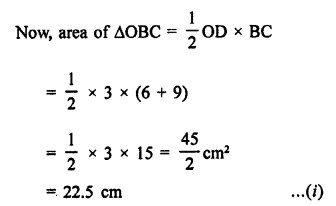
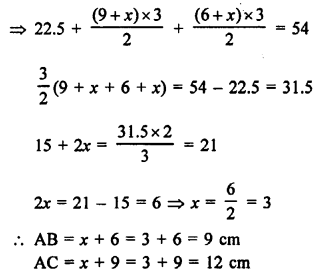
Question 13.
Solution:
In the given figure, PQ is a chord of the circle with centre O.
TP and TQ are tangents, OP and OT are joined.
Radius of the circle is 3 cm and PQ = 4.8 cm.

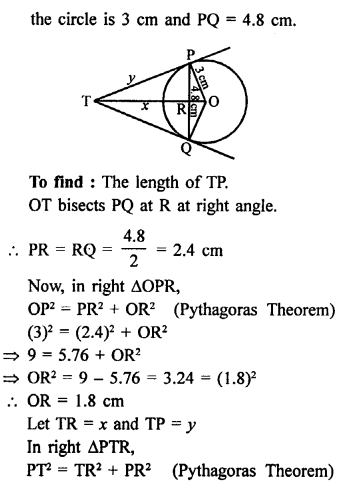
Question 14.
Solution:
PQ and RS are two parallel tangents which
touches the circle at A and B. O is the centre of the circle.
OA and OB are joined.
To prove : AB passes through the centre O of the circle.
Construction : Draw OC || PQ or RS.

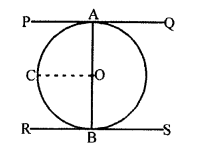
Proof : OA is radius and PQ is tangent.
OA ⊥ PQ ⇒ ∠OAP = 90°
Similarly, OB is radius and RS is the tangent
OB ⊥ RS ⇒ ∠OBR = 90°
PQ || OC
∠AOC + ∠OAP = 180° (Co-interior angles)
∠AOC + 90° = 180°
∠AOC = 180° – 90° = 90°
Similarly, ∠BOC = 90°
∠AOC + ∠BOC = 90° + 90° = 180°
AOB is a straight line.
Hence, AB passes through the centre of the circle.

Question 15.
Solution:
In the given figure, a circle with centre O, is inscribed in a quadrilateral ABCD.
The circle touches the siaes of quadrilateral at P, Q, R and S respectively.
AB = 29 cm, AD = 23 cm, ∠B = 90°
DS = 5 cm
To find : The radius of the circle.
Construction : Join OP and OQ.
Proof: Let OP = OQ = r
∠B = 90°
PBQO is a square.
DR and DS are the tangents to the circle.
DR = DS = 5 cm
AR = AD – DR = 23 – 5 = 18 cm
AR and AQ are tangents to the circle.
AQ = AR = 18 cm
QB = AB – AQ = 29 – 18 = 11 cm
PBQO is a square.
OP = OQ = BQ = 11 cm
Hence, radius of the circle (r) = 11 cm

Question 16.
Solution:
In the given figure, TP is the tangent from an external point T and ∠PBT = 30°.
To prove : BA : AT = 2 : 1
Proof: ∠APB = 90° (Angle in a semicircle)
∠PBT = 30° (given)
∠PAB = 90° – 30° = 60°
But, ∠PAT + ∠PAB = 180° (Linear pair)
⇒ ∠PAT + 60° = 180°
⇒ ∠PAT = 180° – 60° = 120°
and ∠APT = ∠PBA = 30° (Angles in the alternate segment)
In ∆PAT,
∠PTA = 180° – (120° + 30°) = 180° – 150° = 30°
PA = AT
In right ∆APB,

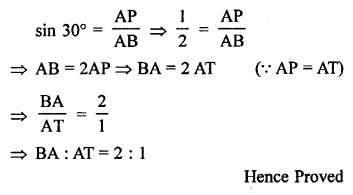
Hope given RS Aggarwal Solutions Class 10 Chapter 12 Circles Ex 12A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.