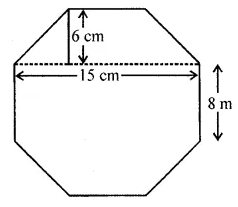
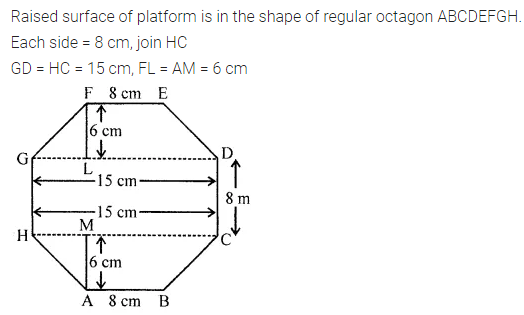
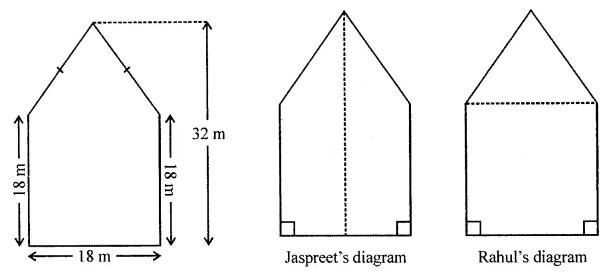
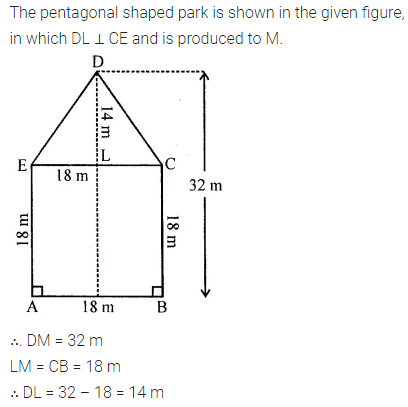
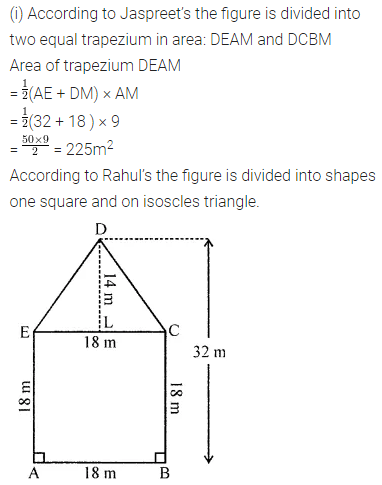
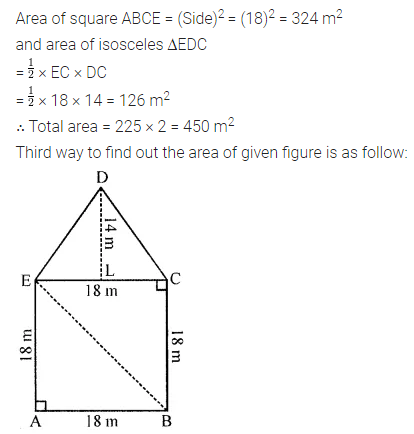
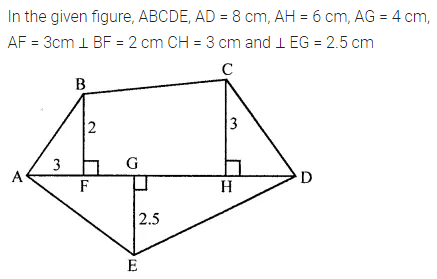
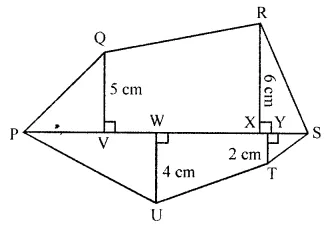
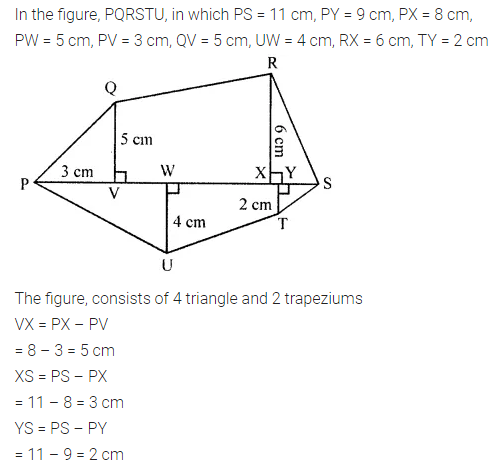
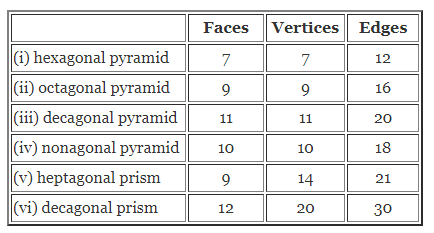
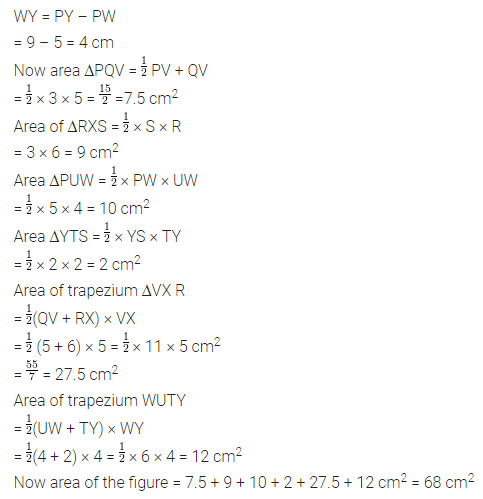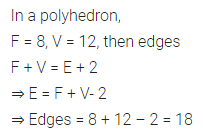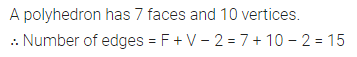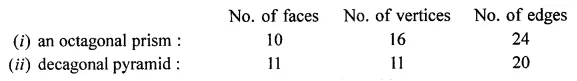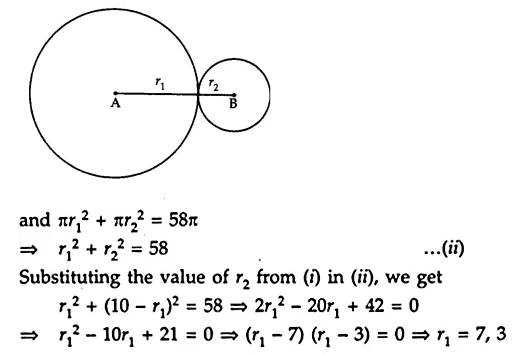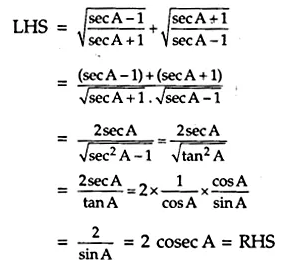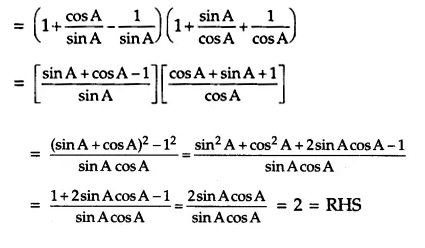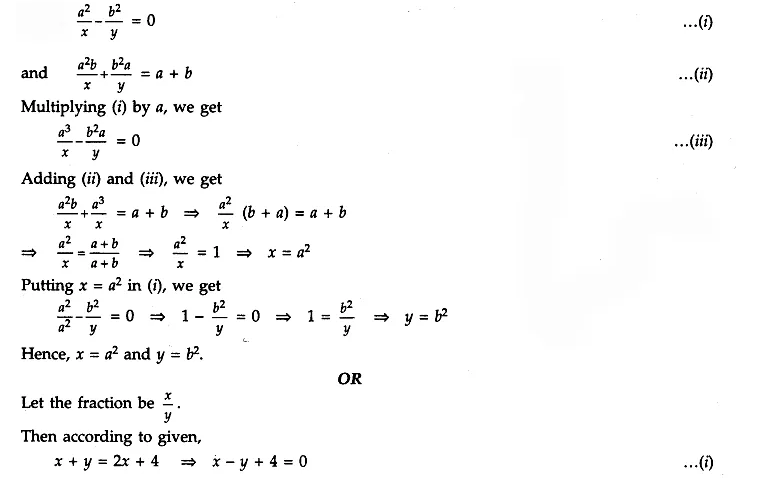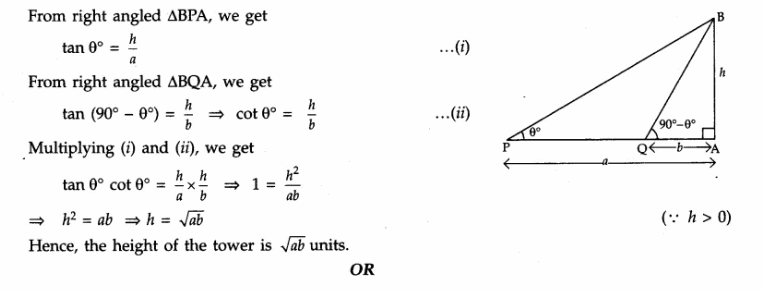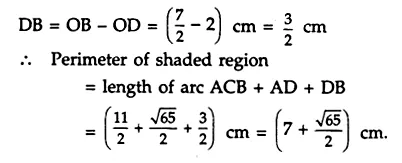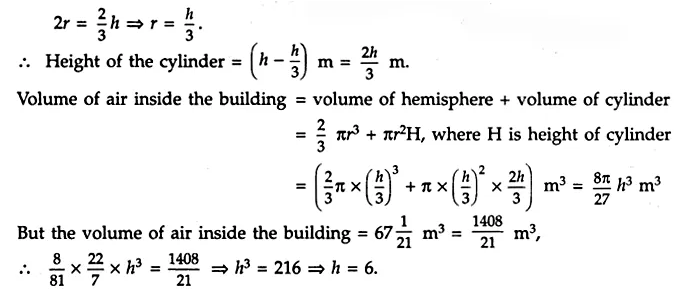ML Aggarwal Class 8 Solutions for ICSE Maths Chapter 18 Mensuration Ex 18.3
Question 1.
The volume of a cube is 343 cm3, find the length of an edge of cube.
Solution:
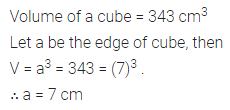
Question 2.
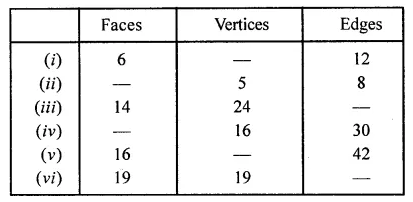
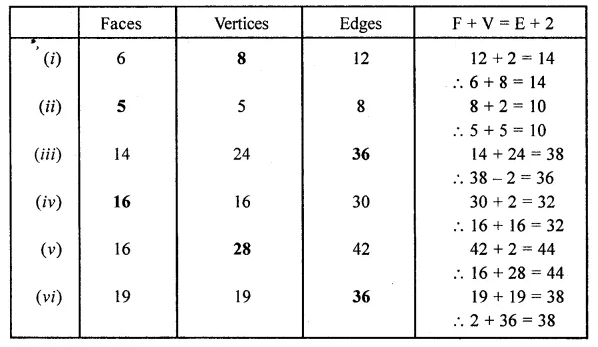
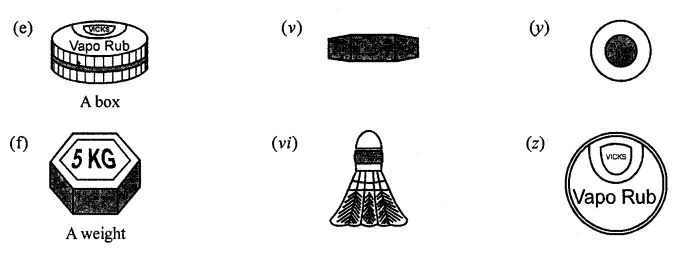
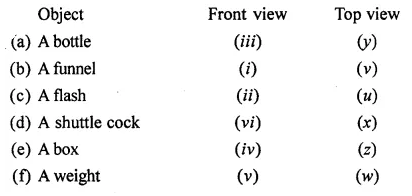
Fill in the following blanks:

Solution:

Question 3.
Find the height of a cuboid whose volume is 312 cm3 and base area is 26 cm2.
Solution:
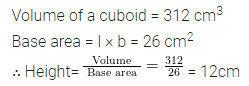
Question 4.
A godown is in the form of a cuboid of measures 55 m × 45 m × 30 m. How many cuboidal boxes can be stored in it if the volume of one box is 1.25 m3?
Solution:

Question 5.
A rectangular pit 1.4 m long, 90 cm broad and 70 cm deep was dug and 1000 bricks of base 21 cm by 10.5 cm were made from the earth dugout. Find the height of each brick.
Solution:

Question 6.
If each edge of a cube is tripled, then find how many times will its volume become?
Solution:
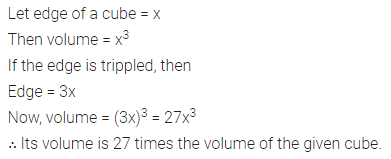
Question 7.
A milk tank is in the form of cylinder whose radius is 1.4 m and height is 8 m. Find the quantity of milk in litres that can be stored in the tank.
Solution:

Question 8.
A closed box is made of 2 cm thick wood with external dimension 84 cm × 75 cm × 64 cm. Find the volume of the wood required to make the box.
Solution:

Question 9.
Two cylindrical jars contain the same amount of milk. If their diameters are in the ratio 3 : 4, find the ratio of their heights.
Solution:
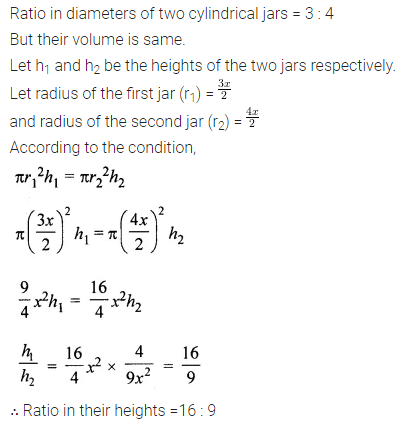
Question 10.
The radius of the base of a right circular cylinder is halved and the height is doubled. What is the ratio of the volume of the new cylinder to that of the original cylinder?
Solution:
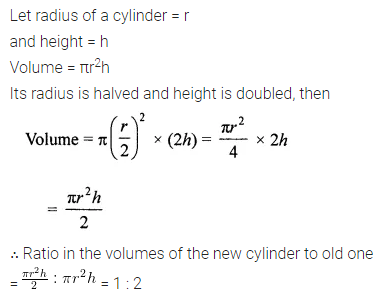
Question 11.
A rectangular piece of a tin of size 30 cm × 18 cm is rolled in two ways, once along its length (30 cm) and once along its breadth. Find the ratio of volumes of two cylinders so formed.
Solution:

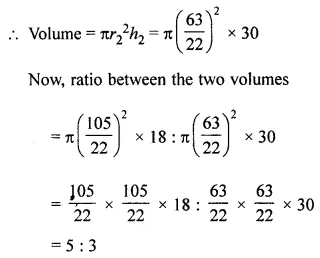
Question 12.
Water flows through a cylindrical pipe of internal diameter 7 cm at 5 m per sec. Calculate
(i) the volume in litres of water discharged by the pipe in one minute.
(ii) the time in minutes, the pipe would take to fill an empty rectangular tank of size 4 m × 3 m × 2.31 m.
Solution:

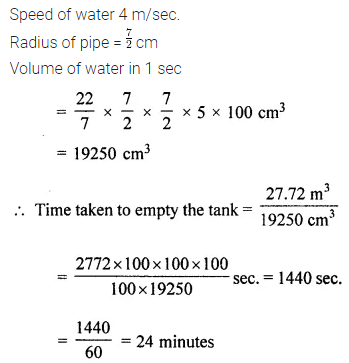
Question 13.
Two cylindrical vessels are filled with milk. The radius of one vessel is 15 cm and the height is 40 cm, and the radius of other vessel is 20 cm and the height is 45 cm. Find the radius of another cylindrical vessel of height 30 cm which may just contain the milk which is in the two given vessels.
Solution:


Question 14.
A wooden pole is 7 m high and 20 cm in diameter. Find its weight if the wood weighs 225 kg per m3 .
Solution:

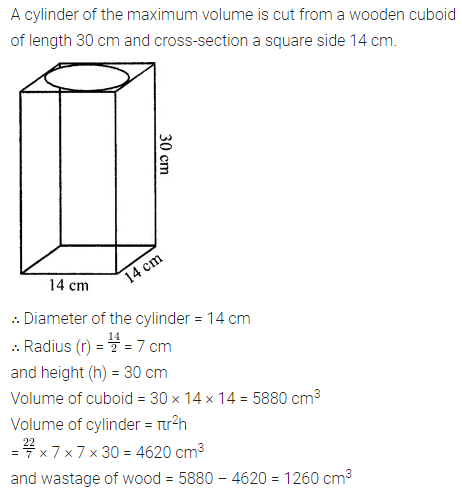
Question 15.
A cylinder of the maximum volume is cut from a wooden cuboid of length 30 cm and cross-section a square of side 14 cm. Find the volume of the cylinder and the volume of the wood wasted.
Solution: