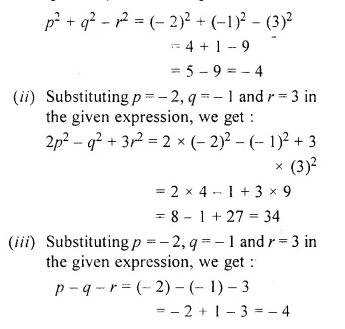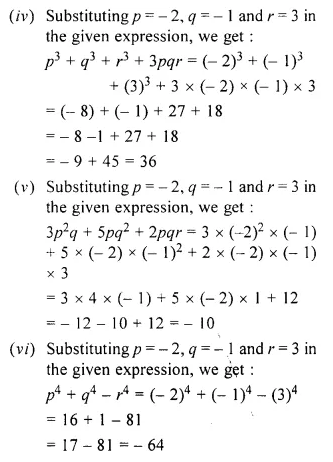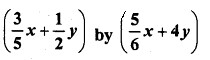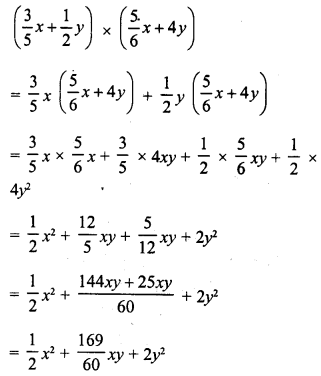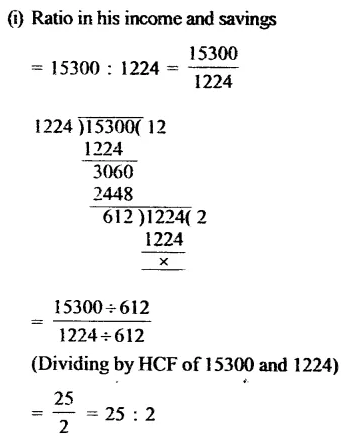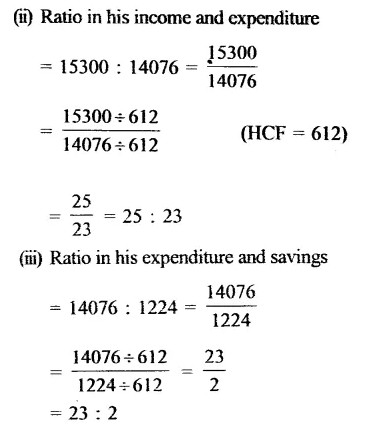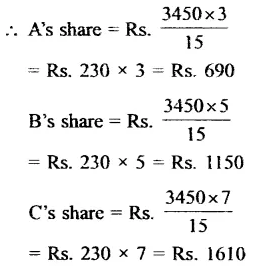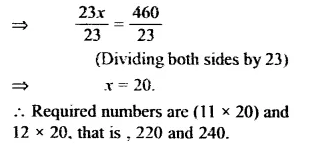CA Foundation Business Economics Study Material – Law of Variable Proportions

CA Foundation Business Economics Study Material Chapter 3 Theory of Production and Cost – Law of Variable Proportions

Law of Variable Proportions

  • The Law of Variable Proportions examines the production function i.e. the input-output relation in short run where one factor is variable and other factors of production are fixed.
  • In other words, it examines production function when the output is increased by varying the quantity of one input.
  • Thus, the law examines the effect of change in the proportions between fixed and variable factor inputs on output in three stages viz. Increasing returns, diminishing returns and negative returns.

Statement of the Law :-
“As the proportion of one factor in a combination of factors is increased, after a point first the marginal and then the average product of that factor will diminish”. (F. Benhan)

The law operates under some assumptions which are as follows:-

  1. There is only one factor which is variable. All other factors remain constant.
  2. All units of variable factor are homogeneous
  3. It is possible to change the proportions in which the various factors are combined.
  4. The state of technology is given and is constant.

The three stages of the law can be explained with the help of the following schedule and diagram.

CA Foundation Business Economics Study Material - Law of Variable Proportions

Stage I: The Law of Increasing Returns to Factor –

  • During this stage, total product (TP) increases at an increasing rate upto the point of inflexion ‘I’ and thereafter it increases at diminishing rate.
  • This is because marginal product (MP) of the variable factor increases upto point ‘M’ on MP curve and then start falling.
  • Rising MP also pulls up average product (AP), which goes on rising, in the first stage.
  • Rising AP indicates increase in the efficiency of variable factor i.e. labour.
  • Stage I ends where AP is maximum and is equal to MP as shown by point ‘C’ in the diagram.

The law of increasing returns operates because of the following two reasons:

1. Indivisibility of fixed factors

  • Due to indivisibility, the quantity of fixed factors is more than the quantity of variable factors.
  • So when the quantity of variable factors is increased to work with fixed factors, output increases speedily due to full and effective utilisation of fixed factors.
  • In other words, efficiency of fixed factors increases.

2. Efficiency of Variable Factor Increases
Due to increase in the quantity of variable factor, it becomes possible to introduce DIVISION OF LABOUR leading to SPECIALISATION. This results in more output per worker.

Stage II: The Law of Diminishing Returns to Factor –

  • In second stage, TP continues to increase at diminishing rate. It reaches the maximum at point ‘D’ in the diagram, where the second stage ends.
  • In this stage, both AP and MP of variable factor are falling- though remains positive. That is why this stage is called as the stage of diminishing returns.
  • At the end of this stage MP becomes, zero as shown by point ‘B’ in the diagram and corresponding to highest point ‘D’ on TP curve.

The law of diminishing returns operate due to the following two reasons:

1. Indivisibility of fixed factors

  • Once the optimum proportion between indivisible fixed factors and variable factors is reached (as in Stage I) with any further increase in the quantity of Variable factor, the fixed factors become inadequate and are overutilised.
  • The fine balance between fixed and variable factor gets disturbed. This causes AP and MP to diminish.

2. Imperfect Substitutability of factors

  • Variable factors are not perfect substitute of fixed factors.
  • The elasticity of substitution between factors is not infinite.

Stage III: The Law of Negative Returns to Factor –

  • In third stage, TP falls and so, TP curve slopes downward. MP becomes negative and the MP curve goes below the X-axis. AP continues to fall.
  • As the MP of variable factor becomes negative, this stage is called the stage of negative returns.
  • In this stage the efficiency of fixed and variable factors fall and factor ratio becomes highly sub-optimal.

The law of negative returns operate due to the following reasons:

  1. The quantity of the variable factor becomes too excessive compared to fixed factors. They get in each other’s way and so TP falls and MP becomes negative.
  2. Too large number of variable factors also reduce the efficiency of fixed factors.

Conclusion -Where to operate?

  1. A rational firm will not produce either in Stage I or in Stage III.
  2. In stage I, the marginal product of fixed factor is negative as its quantity is more than variable factor.
  3. In stage III, the marginal product of variable factor is negative as its quantity is too large than fixed factor.
  4. Therefore, firm would seek to produce in Stage II where both AP and MP of Variable factor are falling.
  5. At which point to produce in this stage will depend on the prices of factor inputs.

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6

Other Exercises

Question 1.
Write the following squares of bionomials as trinomials :
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 1
Solution:
Using the formulas
(a + b)2 = a2 + 2ab + b2 and (a – b)2 = a2 – 2ab + b2
(i) (a + 2)2 = (a)2 + 2 x a x 2 + (2)2
{(a + b)2 = a2 + 2ab + b2}
= a2 + 4a + 4
(ii) (8a + 3b)2 = (8a)2 + 2 x 8a * 3b + (3b)2 = 642 + 48ab + 9 b2
(iii) (2m+ 1)2 = (2m)2 + 2 x 2m x1 + (1)2
= 4m2 + 4m + 1
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 2
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 3

Question 2.
Find the product of the following binomials :
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 4
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 5
Solution:
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 6
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 7

Question 3.
Using the formula for squaring a binomial, evaluate the following :
(i) (102)2
(ii) (99)2
(iii) (1001)2
(iv) (999)2
(v) (703)2
Solution:
(i) (102)2 = (100 + 2)2
= (100)2 + 2 x 100 x 2 + (2)2
{(a + b)2 = a2 + 2ab + b2}
= 10000 + 400 + 4 = 10404
(ii) (99)2 = (100 – 1)2
= (100)2 – 2 x 100 X 1 +(1)2
{(a – b)2 = a2 – 2ab + b2}
= 10000 -200+1
= 10001 -200 =9801
(iii) (1001 )2 = (1000 + 1)2
{(a + b)2 = a2 + 2ab + b2}
= (1000)2 + 2 x 1000 x 1 + (1)2
= 1000000 + 2000 + 1 = 1002001
(iv) (999)2 = (1000 – 1)2
{(a – b)2 = a2 – 2ab + b2}
= (1000)2 – 2 x 1000 x 1 + (1)2
= 1000000 – 2000 + 1
= 1000001 -2000 = 998001

Question 4.
Simplify the following using the formula:
(a – b) (a + b) = a2 – b2 :
(i) (82)2 (18)2
(ii) (467)2 (33)2
(iii) (79)2 (69)2
(iv) 197 x 203
(v) 113 x 87
(vi) 95 x 105
(vii) 1.8 x 2.2
(viii) 9.8 x 10.2
Solution:
(i) (82)2 – (18)2 = (82 + 18) (82 – 18)
{(a + b)(a- b) = a2 – b2} = 100 x 64 = 6400
(ii) (467)2 – (33)2 = (467 + 33) (467 – 33)
= 500 x 434 = 217000
(ii) (79)2 – (69)2 = (79 + 69) (79 – 69)
148 x 10= 1480
(iv) 197 x 203 = (200 – 3) (200 + 3)
= (200)2 – (3)2
= 40000-9 = 39991
(v) 113 x 87 = (100 + 13) (100- 13)
= (100)2 – (13)2
= 10000- 169 = 9831
(vi) 95 x 105 = (100 – 5) (100 + 5)
= (100)2 – (5)2
= 10000 – 25 = 9975
(vii) 8 x 2.2 = (2.0 – 0.2) (2.0 + 0.2)
= (2.0)2 – (0.2)2
= 4.00 – 0.04 = 3.96
(viii)9.8 x 10.2 = (10.0 – 0.2) (10.0 + 0.2)
(10.0)2 – (0.2)2
= 100.00 – 0.04 = 99.96

Question 5.
Simplify the following using the identities :
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 8
Solution:
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 9
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 10

Question 6.
Find the value of x, if
(i)  4x = (52)2 – (48)2
(ii) 14x = (47)2 – (33)2
(iii)  5x = (50)2 – (40)2
Solution:
(i) 4x = (52)2 – (48)2
⇒ 4x = (52 + 48) (52 – 48)
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 11

Question 7.
If x + \(\frac { 1 }{ x }\)= 20, find the value of x2+ \(\frac { 1 }{ { x }^{ 2 } }\)

Solution:
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 12

Question 8.
If x – \(\frac { 1 }{ x }\) = 3, find the values of x2 + \(\frac { 1 }{ { x }^{ 2 } }\) and x4 + \(\frac { 1 }{ { x }^{ 4 } }\)

Solution:
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 13

Question 9.
If x2 – \(\frac { 1 }{ { x }^{ 2 } }\)= 18, find the values of x+ \(\frac { 1 }{ x }\)  and x– \(\frac { 1 }{ x }\)
Solution:
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 14

Question 10.
Ifx+y = 4 and xy = 2, find the value of x2+y2.
Solution:
x + y = 4
Squaring on both sides,
(x + y)2 = (4)2
⇒ x2 +y2 + 2xy = 16
⇒ x2+y2 + 2 x 2 = 16                       (∵ xy = 2)
⇒ x2 + y2 + 4 = 16
⇒ x2+y2 = 16 – 4= 12           ‘
∴ x2+y2 = 12

Question 11.
If x-y = 7 and xy = 9, find the value of x2+y2.
Solution:
x-y = 7
Squaring on both sides,
(x-y)2 = (7)2
⇒ x2+y2-2xy = 49
⇒ x2 + y2 – 2 x 9 = 49                    (∵ xy = 9)
⇒ x2 +y2 – 18 = 49
⇒ x2 + y2 = 49 + 18 = 67
∴ x2+y2 = 67

Question 12.
If 3x + 5y = 11 and xy = 2, find the value of 9x2 + 25y2
Solution:
3 x + 5y = 11, xy = 2
Squaring on both sides,
(3x + 5y)2 = (11)2
⇒ (3x)2 + (5y)2 + 2 x 3x x 5y = 121
⇒ 9x2 + 25y2 + 30 x 7 = 121
⇒ 9x2 + 25y2+ 30 x 2 = 121           (∵ xy = 2)
⇒ 9x2 + 25y2 + 60 = 121
⇒ 9x2 + 25y2 = 121 – 60 = 61
∴ 9x2 + 25y2 = 61

Question 13.
Find the values of the following expressions :
(i)16x2 + 24x + 9, when X’ = \(\frac { 7 }{ 45 }\)
(ii) 64x2 + 81y2 + 144xy when x = 11 and y = \(\frac { 4 }{ 3 }\)
(iii) 81x2 + 16y2-72xy, whenx= \(\frac { 2 }{ 3 }\) andy= \(\frac { 3 }{ 4 }\)
Solution:
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 15
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 16

Question 14.
If x + \(\frac { 1 }{ x }\) = 9, find the values of x4 + \(\frac { 1 }{ { x }^{ 4 } }\).
Solution:
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 17
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 18

Question 15.
If x + \(\frac { 1 }{ x }\) = 12, find the values of x–  \(\frac { 1 }{ x }\).
Solution:
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 19

Question 16.
If 2x + 3y = 14 and 2x – 3y = 2, find the value of xy.
Solution:
2x + 3y = 14, 2x – 3y= 2
We know that
(a + b)2 – (a – b)2 = 4ab
∴ (2x + 3y)2 – (2x – 3y)2 = 4 x 2x x 3y = 24xy
⇒ (14)2 – (2)2 = 24xy
⇒ 24xj= 196-4= 192
⇒ xy = \(\frac { 192 }{ 24 }\) = 8
∴  xy = 8

Question 17.
If x2 + y2 = 29 and xy = 2, find the value of
(i) x+y
(ii) x-y
(iii) x4 +y4
Solution:
x2 + y2 = 29, xy = 2
(i) (x + y)2 = x2 + y2 + 2xy
= 29 + 2×2 = 29+ 4 = 33
∴  x + y= ±√33
(ii) (x – y)2 = x2 + y2 – 2xy
= 29- 2×2 = 29- 4 = 25
∴ x-y= ±√25= ±5
(iii) x2 + y2 = 29
Squaring on both sides,
(x2 + y2)2 = (29)2
⇒ (x2)2 + (y2)2 + 2x2y2 = 841
⇒ x4 +y + 2 (xy)2 = 841
⇒ x4 + y + 2 (2)2 = 841          (∵ xy = 2)
⇒ x4 + y + 2×4 = 841
⇒ x4 + y + 8 = 841
⇒ x4 + y = 841 – 8 = 833
∴ x4 +y = 833

Question 18.
What must be added to each of the following expressions to make it a whole square ?’
(i) 4x2 – 12x + 7
(ii) 4x2 – 20x + 20
Solution:
(i) 4x2 – 12x + 7 = (2x)2 – 2x 2x x 3 + 7
In order to complete the square,
we have to add  32 – 7 = 9 – 7 = 2
∴ (2x)2 – 2 x 2x x 3 + (3)2
= (2x-3)2
∴ Number to be added = 2
(ii) 4x2 – 20x + 20
⇒ (2x)2 – 2 x 2x x 5 + 20
In order to complete the square,
we have to add (5)2 – 20 = 25 – 20 = 5
∴ (2x)2 – 2 x 2x x 5 + (5)2
= (2x – 5)2
∴ Number to be added = 5

Question 19.
Simplify :
(i) (x-y) (x + y) (x2 + y2) (x4 + y4)
(ii) (2x – 1) (2x + 1) (4x2 + 1) (16x4 + 1)
(iii) (7m – 8m)2 + (7m + 8m)2
(iv) (2.5p -5q)2 – (1.5p – 2.5q)2
(v) (m2 – n2m)2 + 2m3n2
Solution:
(i) (x – y) (x + y) (x2 + y2) (x4 +y)
= (x2 – y2) (x2 + y) (x4 + y4)
= [(x2)2 – (y2)2] (x4+y4)
= (x4-y4) (x4+y4)
= (x4)2 – (y4)2 = x8 – y8
(ii) (2x – 1) (2x + 1) (4x2 + 1) (16x4 + 1)
= [(2x)2 – (1)2] (4x2 + 1) (16x4 + 1)
= (4x2 – 1) (4x2 + 1) (16x4 + 1)
= [(4x2)2-(1)2] (16x4+ 1)
= (16x4-1) (16x4+ 1)
= (16x4)2– (1)2 = 256x8 – 1
(iii) (7m – 8m)2 + (7m + 8n)2
= (7m)2 + (8n)2 – 2 x 7m x 8n + (7m)2 + (8n)2 + 2 x 7m x 8n
= 49m2 + 64m2 – 112mn + 49m2 + 64m2 + 112mn
= 98 m2 + 128n2
(iv) (2.5p – 1.5q)2 – (1.5p – 2.5q)2
= (2.5p)2 + (1.5q)2 – 2 x 2.5p x 1.5q
= [(1.5p)2 + (1.5q)2 – 2 x 1.5 p x 2.5q]
= (6.25p2 + 2.25q2 – 7.5 pq) – (2.25p2 + 6.25q2-7.5pq)
= 6.25p2 + 2.25q2 – 7.5pq – 2.25p2 – 6.25q2 + 7.5pq
= 6.25p2 – 2.25p2 + 2.25g2 – 6.25q2
= 4.00P2 – 4.00q2
= 4p2 – 4q2 = 4 (p2 – q2)
(v) (m2 – n2m)2 + 2m3M2
= (m2)2 + (n2m)2 -2 x m2 x n2m + 2;m3m2
= m4 + n4m2 – 2m3n2 + 2m3n2
= m4 + n4m2 = m4 + m2n4

Question 20.
Show that :
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 20
Solution:
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 21
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 22

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8D

RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8D

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8D.

Other Exercises

Simplify :

Question 1.
Solution:
We have : a – (b – 2a)
= a – b + 2a
= a + 2a – b
= (1 + 2) a – b
= 3a – b.

Question 2.
Solution:
We have : 4x – (3y – x + 2z)
= 4x – 3y + x – 2z
= 4x + x – 2y – 2z
= 5x – 3y – 2z

Question 3.
Solution:
We have :
(a2 + b2 + 2ab) – (a2 + b2 – 2ab)
= a2 + b2 + 2ab – a2 – b2 + 2ab
= a2 – a2 + b2 – b2 + 2ab + 2ab
= 0 + 0 + (2 + 2) ab
= 4 ab

Question 4.
Solution:
We have :
– 3 (a + b) + 4 (2a – 3b) – (2a – b)
= – 3a – 3b + 8a – 12b – 2a + b
= – 3a + 8a – 2a – 3b – 12b + b
= ( – 3 + 8 – 2) a + ( – 3 – 12 + 1) b
= 3a – 14 b.

Question 5.
Solution:
We have :
– 4x2 + {(2x2 – 3) – (4 – 3x2)}
= – 4x2 + {2x2 – 3 – 4 + 3x2}
[removing grouping symbol]
= – 4x2 + {5x2 – 7)
= – 4x2 + 5x2 – 7
(removing grouping symbol {})
= x2 – 7

Question 6.
Solution:
We have :
– 2 (x2 – y2 + xy) – 3 (x2 + y2 – xy)
= – 2x2 + 2y2 – 2xy – 3x2 – 3y2 + 3xy
= – 2x2 – 3x2 + 2y2 – 3y2 – 2xy + 3xy
= ( – 2 – 3)x2 + (2 – 3) y2 + ( – 2 + 3)xy
= – 5x2 – y2 + xy

Question 7.
Solution:
a – [2b – {3a – (2b – 3c)}]
= a – [2b – {3a – 2b + 3c}]
[removing grouping symbol( )]
= a – [2b – 3a + 2b – 3c]
(removing grouping symbol {})
= a – [4b – 3a – 3c]
= a – 4b + 3a + 3c
(removing grouping symbol [ ])
= 4a – 4b + 3c

Question 8.
Solution:
Removing the innermost grouping symbol ( ) first, then { } and then [ ], we have :
– x + [5y – {x – (5y – 2x)}]
= – x + [5y – {x – 5y + 2x}]
= – x + [5y – {3x – 5y}]
= – x + [5y – 3x + 5y]
= – x + [ 10y – 3x]
= – x + 10y – 3x
= – x – 3x + 10y
= – 4x + 10y

Question 9.
Solution:
Removing the innermost grouping symbol ( ) first, then { } and then [ ], we have :
86 – [15x – 7 (6x – 9) – 2 {10x – 5(2 – 3x)}]
= 86 – [15x – 42x + 63 – 2 {10x – 10 + 15x}
= 86 – [ 15x – 42x + 63 – 2 {25x – 10}]
= 86 – [15x – 42x + 63 – 50x + 20]
= 86 – 15x + 42x – 63 + 50x – 20
= (86 – 63 – 20) – 15x + 42x + 50x
= (86 – 83) + (- 15 + 42 + 50) x
= 3 + 77x

Question 10.
Solution:
Removing the innermost grouping ‘ symbol () first, then { } and then [ ], we have :
12x – [3x3 + 5x2 – {7x2 – (4 – 3x – x3) + 6x3} – 3x]
= 12x – [3x3 – 5x2 – {7x2 – 4 + 3x + x3 + 6x3} – 3x]
= 12x – [3x3 + 5x2 – {7x2 – 4 + 3x + 7x3} – 3x]
= 12x – [3x3 + 5x2 – 7x2 + 4 – 3x – 7x3 – 3x]
= 12x – [3x3 – 7x3 + 5x2 – 7x2 + 4 – 3x – 3x]
= 12x – [ – 4x3 + 2x2 + 4 – 6x]
= 12x + 4x3 + 2x2 – 4 + 6x
= 12x + 6x + 4x3 + 2x2 – 4
= 18x + 4x3 + 2x2 – 4
= 4x3 + 2x2 + 18x – 4

Question 11.
Solution:
Removing the innermost grouping symbol ( ) first, then { } and then [ ], we have
5a – [a2 – {2a (1 – a + 4a2) – 3a (a2 – 5a – 3)}] – 8a
= 5a – [a2 – {2a – 2a2 + 8a3 – 3a3 + 15a2 + 9a}] – 8a
= 5a – [a2 – {2a + 9a – 2a2 + 15a2 + 8a3 – 3a3}] – 8a
= 5a – [a2 – {11a + 13a2 + 5a3}] – 8a
= 5a – [a2 – 11a – 13a2 – 5a3] – 8a
= 5a – a2 + 11a + 13a2 + 5a3 – 8a
= 5a + 11a – 8a – a2 + 13a2 + 5a3
= 8a + 12a2 + 5a3
= 5a3 + 12a2 + 8a.

Question 12.
Solution:
Removing the innermost grouping symbol ( ) first, then { } and then [ ], we have :
3 – [x – {2y – (5x + y – 3) + 2x2} – (x2 – 3y)]
= 3 – [x – {2y – 5x – y + 3 + 2x2} – x2 + 3y]
= 3 – [x – {y – 5x + 3 + 2x2} – x2 + 3y]
= 3 – [x – y + 5x – 3 – 2x2 – x2 + 3y]
= 3 – [6x + 2y – 3 – 3x2]
= 3 – 6x – 2y + 3 + 3x2
= 6 – 6x – 2y + 3x2

Question 13.
Solution:
Removing the innermost grouping symbol ( ) first, then { } and then [ ], we have :
xy – [yz – zx – {yx – (3y – xz} – (xy – zy)}]
= xy – [yz – zx – {yx – 3y + xz – xy + zy}]
= xv – [yz – zx – {- 3y + xz + zy}]
= xy – [yz – zx + 3y – xz – zy]
= xy – [ – 2xz + 3y]
= xy + 2xz – 3y

Question 14.
Solution:
Removing the innermost grouping symbol ( ) first, then { } and then [ ], we have
2a – 3b – [3a – 2b – {a – c – (a – 2b)}]
= 2a – 3b – [3a – 2b – {a – c – a + 2b}]
= 2a – 3b – [3a – 2b – { – c + 2b}]
= 2a – 3b – [3a – 2b + c – 2b]
= 2a – 3b – 3a + 2b – c + 2b
= 2a – 3a – 3b + 2b + 2b – c
= – a + b – c

Question 15.
Solution:
Removing the innermost grouping symbol () first, then { } and ten [ ], we have:
– a – [a + {a + b – 2a – (a – 2b)} – b]
= – a – [a + {a + b – 2a – a + 2b} – b]
= – a – [a + { – 2a + 3b} – b]
= – a – [a – 2a + 3b – b]
= – a – a + 2a – 3b + b
= – 2a + 2a – 2b
= – 2 b

Question 16.
Solution:
Removing the innermost grouping symbol ‘—’ first, then ( ), then { } and then [ ], we have
2a – [4b – {4a – (3b – \(\overline { 2a+2b } \))}]
= 2a – [4b – {4a – (3b – 2a – 2b)}]
= 2a – [4b – {4a – (b – 2a)}]
= 2a – [4b – {4a – b + 2a}]
= 2a – [4b – {6a – b}]
= 2a – [4b – 6a + b]
= 2a – [5b – 6a]
= 2a – 5b + 6a
= 8a – 5b.

Question 17.
Solution:
Removing the innermost grouping < symbol ( ) first, then { } and then [ ], we have :
5x – [4y – {7x – (3z – 2y) + 4z – 3(x + 3y – 2z)}]
= 5x – [4y – {7x – 3z + 2y + 4z – 3x – 9y + 6z}]
= 5x – [4y – {4x + 7z – 7y}]
= 5x – [4y – 4x – 7z + 7y]
= 5x – [11y – 4x – 7z]
= 5x – 11y + 4x + 7z
= 9x – 11y + 7z

Hope given RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C

RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8C.

Other Exercises

Question 1.
Solution:
(i) The required sum
= 3x + 7x
= (3 + 7) x
= 10x
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q1.1
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q1.2

Question 2.
Solution:
(i) Adding columnwise,
we get
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q2.1
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q2.2

Question 3.
Solution:
(i) Arranging the like terms columnwise and adding, we get :
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q3.1
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q3.2
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q3.3

Question 4.
Solution:
(i) We have :
2x – 5x = (2 – 5)x = – 3x
(ii) We have :
6x – y – (- xy) = 6xy + xy = 7xy
(iii) We have : 5b – 3a
(iv) We have : 9y – ( – 7x) = 9y + 7x
(v) We have : – 7x2 – 10x2 = ( – 7 – 10)x2
= – 17x2
(vi) We have : b2 – a2 – (a2 – b2)
= b2 – a2 – a2 + b2
= b2 + b2 – a2 – a2
= (1 + 1) b2 + ( – 1 – 1) a2
= 2b2 – 2a2

Question 5.
Solution:
(i) Arranging the like terms columnwise, we get :
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q5.1
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q5.2
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q5.3
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q5.4

Question 6.
Solution:
(i) Rearranging and collecting the like terms, we get :
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q6.1
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q6.2

Question 7.
Solution:
We have:
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q7.1

Question 8.
Solution:
We have :
A = 7x2 + 5xy – 9y2
B = – 4x2 + xy + 5y2
C = 4y2 – 3x2 – 6xy
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q8.1
= 0+0+0 = 0
Hence the result

Question 9.
Solution:
Required expression
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q9.1

Question 10.
Solution:
Substituting the values of P, Q, R and S, we have :
P + Q + R + S = (a2 – b2 + 2ab)
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q10.1

Question 11.
Solution:
Required expression
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q11.1

Question 12.
Solution:
Required expression
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q12.1

Question 13.
Solution:
Required expression
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q13.1

Question 14.
Solution:
Required expression
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q14.1

Question 15.
Solution:
Sum of 5x – 4y + 6z and – 8x + y – 2z
= 5x – 4y + 6z – 8x + y – 2z
= 5x – 8x – 4y + y + 6z – 2z
= – 3x – 3y + 4z
Sum of 12x – y + 3z and – 3x + 5y – 8z
= 12x – y + 3z – 3x + 5y – 8z
= 12x – 3x – y + 5y + 3z – 8z
= 9x + 4y – 5z
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q15.1

Question 16.
Solution:
Required expression
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q16.1

Question 17.
Solution:
Required expression
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8C Q17.1

Hope given RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8B

RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8B.

Other Exercises

Question 1.
Solution:
(i) Substituting a = 2 and b = 3 in the , given expression, we get :
a + b = 2 + 3 = 5
(ii) Substituting a = 2 and b = 3 in the given expression, we get :
a2 + ab = (2)2 + 2 x 3
= 4 + 6 = 10
(iii) Substituting a = 2 and b = 3 in the given expression, we get :
ab – a2 = 2 x 3 – (2)2
= 6 – 4 = 2
(iv) Substituting a = 2 and b = 3 in the given expression, we get :
2a – 3b = 2 x 2 – 3 x 3
= 4 – 9 = – 5
(v) Substituting a = 2 and b = 3 in the given expression, we get :
5a2 – 2ab = 5 x (2)2 – 2 x 2 x 3
= 5 x 4 – 4 x 3
= 20 – 12 = 8
(vi) Substituting a = 2 and b = 3 in the given expression, we get :
a3 – b3 = (2)3 – (3)3 = 2 x 2 x 2 – 3 x 3 x 3
= 8 – 27 = – 19

Question 2.
Solution:
(i) Substituting x = 1, y = 2 and z = 5 in the given expression, we get :
3x – 2y + 4z = 3 x 1 – 2 x 2 + 4 x 5
= 3 – 4 + 20 = 23 – 4 = 19
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8B Q2.1
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8B Q2.2

Question 3.
Solution:
(i) Substituting p = – 2, q = – 1 and r = 3
in the given expression, we get :
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8B Q3.1
RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8B Q3.2

Question 4.
Solution:
(i) The coefficient of x in 13x is 13
(ii) The coefficient of y in – 5y is – 5
(iii) The coefficient of a in 6ab is 6b
(iv) The coefficient of z in – 7xz is – 7x
(v) The coefficient of p in – 2pqr is – 2qr
(vi) The coefficient of y2 in 8xy2z is 8xz
(vii) The coefficient of x3 in x3 is 1
(viii) The coefficient of x2 in – x2 is -1

Question 5.
Solution:
(i) The numerical coefficient of ab is 1
(ii) The numerical coefficient of – 6bc is – 6
(iii) The numerical coefficient of 7xyz is 7
(iv) The numerical coefficient of – 2x3y2z is – 2.

Question 6.
Solution:
(i) The constant term is 8
(ii) The constant term is – 9
(iii) The constant term is \(\\ \frac { 3 }{ 5 } \)
(iv) The constant term is \(– \frac { 8 }{ 3 } \)

Question 7.
Solution:
(i) The given expression contains only one term, so it is monimial.
(ii) The given expression contains only two terms, so it is binomial.
(iii) The given expression contains only one term, so it is monomial.
(iv) The given expression contains three terms, so it is trinomial.
(v) The given expression contains three terms, so it is trinomial.
(vi) The given expression contains only one term, so it is monomial.
(vii) The given expression contains four terms, so it is none of monomial, binomial and trinomial.
(viii) The given expression contains only one term so it is monomial.
(ix) The given expression contains two terms, so it is binomial.

Question 8.
Solution:
(i) The terms of the given expression 4x5 – 6y4 + 7x2y – 9 are :
4x5, – 6y4, 7x2y, – 9
(ii) The terms of the given expression 9x3 – 5z4 + 7x3y – xyz are :
9x3, – 5z4, 7x3y, – xyz.

Question 9.
Solution:
(i) We have : a2, b2, – 2a2, c2, 4a
Here like terms are a2, – 2a2
(ii) We have : 3x, 4xy, – yz, \(\\ \frac { 1 }{ 2 } \) zy
Here like terms are – yz, \(\\ \frac { 1 }{ 2 } \) zy
(iii) We have : – 2xy2, x2y, 5y2x, x2z
Here like terms are – 2xy2, 5y2x
(iv) We have :
abc, ab2c, acb2, c2ab, b2ac, a2bc, cab2
Here like terms are ab2c, acb2, b2ac, cab2.

Hope given RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8A

RS Aggarwal Class 6 Solutions Chapter 8 Algebraic Expressions Ex 8A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8A.

Other Exercises

Question 1.
Solution:
(i) x + 12
(ii) y – 7
(iii) a – b
(iv) (x + y) + xy
(v) \(\\ \frac { 1 }{ 3 } \)x (a + b)
(vi) 7y + 5x
(vii) \(x+ \frac { y }{ 5 } \)
(viii) 4 – x
(ix) \(\\ \frac { x }{ y } -2\)
(x) x2
(xi) 2x + y
(xii) y2 + 3x 
(xiii) x – 2y
(xiv) y3 – x3
(xv) \(\\ \frac { x }{ 8 } \times y\)

Question 2.
Solution:
Marks scored in English = 80
Marks scored in Hindi = x
∴ Total score in the two subjects = 80 + x

Question 3.
Solution:
We can write :
(i) b × b × b ×….15 times = 615
(ii) y × y × y ×…..20 times = y20
(iii) 14 × a × a × a × a × b × b × b= 14a4 b3
(iv) 6 × x × x × y × y = 6x2y2
(v) 3 × z × z × z × y × y × x= 3z3y2x

Question 4.
Solution:
We can write :
(i) x2y4 = x × x × y × y × y × y
(ii) 6y5 = 6 × y × y × y × y × y
(iii) 9xy2z = 9 × x × y × y × z
(iv) 10a3b3c3 = 10 × a × a × a × b × b × b × c × c × c

 

Hope given RS Aggarwal Solutions Class 6 Chapter 8 Algebraic Expressions Ex 8A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5

RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5

Other Exercises

Multiply:

Question 1.
(5x + 3) by (7x + 2)
Solution:
(5x + 3) x (7x + 2)
= 5x (7x + 2) + 3 (7x + 2)
= 35x2 + 10x + 21x + 6
= 35x2 + 31x + 6

Question 2.
(2x + 8) by (x – 3)
Solution:
(2x + 8) x (x – 3)
= 2x (x – 3) + 8 (x – 3)
= 2x2 – 6x + 8x – 24
= 2x2 + 2x – 24

Question 3.
(7x +y) by (x + 5y)
Solution:
(7x + y) x (x + 5y)
= 7x (x + 5y) + y (x + 5y)
= 7x2 + 35xy + xy + 5y2
=7x2 + 36xy + 5y2

Question 4.
(a – 1) by (0.1a2 + 3)
Solution:
(a – 1) x (0.1a2 + 3)
= a (0.1a2 + 3) – 1 (0.1a2+ 3)
= 0.1a3 + 3a-0.1a2-3
= 0.1a3 – 0.1a2 + 3a-3

Question 5.
(3x2 +y2) by (2x2 + 3y2)
Solution:
(3x2+y2) x (2x2 + 3y2)
= 3x2 (2x2 + 3y2) + y2(2x2 + 3y2)
= 6x2 +2 + 9x2y2 + 2x2y2 + 3y2 + 2
= 6x4 + 11 x2y2 + 3y4

Question 6.
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5 1
Solution:
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5 2

Question 7.
(x6-y6) by (x2+y2)
Solution:
(x6 – y6) x (x2 + y2)
= x6 (x2 + y2) – y6 (x2 + y2)
= x6 x x2 + x6y2 – x2y6 -y6 x y2
= x6 + 2 + x6y2 – x2y6 – y6 +2
= x  + x6y2 – x2y6 – y8

Question 8.
(x2 + y2) by (3a+2b)
Solution:
(x2 + y2) x (3a + 2b)
= x2 (3a + 2b) + y2 (3a + 2b)
= 3x2a + 2x2b + 3y2a + 2y2b
3ax2 + 3av2 + 2bx2 + 2by2

Question 9.
[-3d + (-7ƒ)] by (5d +ƒ)
Solution:
[-3d + (-7ƒ)] x (5d +ƒ)
= -3d x (5d +ƒ) + (-7ƒ) x (5d +ƒ)
= -15d2-3dƒ- 35dƒ- 7ƒ2
= -15d2 – 38dƒ- 7ƒ2

Question 10.
(0.8a – 0.5b) by (1.5a -3b)
Solution:
(0.8a – 0.5b) x (1.5a-3b)
= 0.8a x (1.5a – 36) – 0.56 (1.5a -3b)
= 1.2a2 – 2.4ab – 0.75ab + 1.5b2
= 1.2a2-3.15ab+ 1.5b2

Question 11.
(2x2 y2 – 5xy2) by (x2 -y2)
Solution:
(2x2 y2 – 5xy2) x (x2 -y2)
= 2x2y2 (x2 – y2) – 5x_y2 (x2 – y2)
= 2x2y2 x x2 – 2x2y2 xy2– 5xy2 x x2 + 5x2 xy2
= 2x2 + 2 y2– 2x2 x y2 + 2– 5x1+2 y2+5xy2 + 2
= 2x4y2– 2x2y4 – 5x3y2+ 5xy4

Question 12.
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5-q12
Solution:
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5 3

Question 13.
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5 4
Solution:
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5 5
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5 6

Question 14.
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5 7
Solution:
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5 8

Question 15.
(2x2-1) by (4x3 + 5x2)
Solution:
(2x2-1)x(4x3 + 5x2)
= 2x2 x (4x3 + 5x2) – 1 (4x3 + 5x2)
= 2x2 x 4x3 + 2x2 x 5x2 – 4x3 – 5x2
= 8x2 + 3 + 10x2 + 2-4x3-5x2
= 8x5 + 10x4 – 4x3 – 5x2

Question 16.
(2xy + 3y2) (3y2 – 2)
Solution:
(2xy + 3y2) (3y2 – 2)
= 2xy x (3y2-2) + 3y2 x (3y2-2)
= 2xy x Zy2+ 2xy x (-2) + Zy2 x Zy2 – Zy2 x 2
= 6xy1 + 2– 4xy + 9y2 + 2– 6y2
= 6xy3 – 4xy + 9y4– 6y2
Find the following products and verify the result for x = -1, y = -2 :

Question 17.
(3x-5y)(x+y)
Solution:
(3x-5y)(x+y)
= 3x x (x + y) – 5y x (x + y)
= 3x x x + 3x x y-5y x x-5y x y
= 3x2 + 3xy – 5xy – 5y2
= 3x2 – 2xy – 5y2
Verfification:
x = -1,y = -2
L.H.S. = (3x-5y)(x+y)
= [3 (-1) -5 (-2)] [-1 – 2]
= (-3 + 10) (-3) = 7 x (-3) = -21
R.H.S. = 3x2 – 2xy – 5y2
= 3 (-1)2 – 2 (-1) (-2) -5 (-2)2
=3×1-4-5×4=3-4-20
= 3-24 = -21
∴ L.H.S. = R.H.S.

Question 18.
(x2y-1) (3-2x2y)
Solution:
(x2y-1) (3-2x2y)
= x2y (3 – 2x2y) -1(3-2x2y)
= x2y x 3 – x2y x 2x2y – 1 x 3 + 1 x 2x2y
= 3x2y-2x2 + 2x y1 +1-3 + 2x2y
= 3x2y – 2x4y2– 3 + 2x2y
= 3x2y + 2x2y – 2x4y2 – 3
= 5x2y – 2x4y2 – 3
Verification : (x = -1, y = -2)
L.H.S. = (x2y – 1) (3 – 2x2y)
= [(-1)2 x (-2) -1] [3 – 2 x (-1)2 x (-2)]
= [1 x (-2) -1) [3 – 2 x 1 x (-2)]
= (-2 – 1) (3 + 4) = -3 x 7 = -21
R.H.S. = 5x2y – 2x4y2 – 3
= 5 (-1)2 (-2) -2 (-1)4 (-2)2 -3
5 x 1 (-2) – 2 (1 x 4) -3
= -10-8-3 = -21
∴ L.H.S. = R.H.S

Question 19.
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5 9
Solution:
RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5 10

Simplify :

Question 20.
x2 (x + 2y) (x – 3y)
Solution:
x2 (x + 2y) (x – 3y)
= x2 [x (x – 3y) + 2y (x – 3y)]
= x2 [x2 – 3xy + 2xy – 6y2]
= x2 [x2 – xy – 6y2)
= x2 x x2 – x2 x xy – x26y2
= x4 – x3y – 6x2y2

Question 21.
(x2 – 2y2) (x + 4y)
Solution:
(x2 – 2y2) (x + 4y) x2y2
= [x2 (x + 4y) -2y2 (x + 4y)] x2y2
= (x3 + 4x2y – 2xy2 – 8y3) x2y2
= x2y2 x x3 + x2y2 x 4x2y – 2x2y2 x xy2 – 8x2y2 x y3
= x2 +3 y2 + 4x2 + 2 y2 +1 – 2x2 +1 y2+ 2 – 8x2y2+3
= xy + 44xy3 – 2x3y4 – 8x2y5

Question 22.
a2b2 (a + 2b) (3a + b)
Solution:
a2b2 (a + 2b) (3a + b)
= a2b2 [a (3a + b).+ 2b (3a + b)]
= a2b2 [3a2 + ab + 6ab + 2b2]
= a2b2 [3a2 + lab + 2b2]
= a2b2 x 3a2 + a2b2 x 7ab + a2b2 x 2b2
= 3a2 + 2b2 + 7a2+1 b2+1+ 2a2b2 + 2
= 3a4b2 + 7a3b3 + 2a2b4

Question 23.
x2 (x-y) y2 (x + 2y)
Solution:
x2 (x -y) y2 (x + 2y)
= [x2 x x – x2 x y] [y2 x x + y2 x 2y]
= (x3 – x2y) (xy2 + 2y3)
= x3 (xy2 + 2y3) – x2y (xy2 + 2y3)
= x3 x xy2 + x3 x 2y3 – x2y x xy2 – x2y x 2y3
= x3 +1 y2 + 2x3y3 – x2 +1 y1+ 2 – 2x2y1 + 3
= x4y2 + 2x3y3 – x3y3 – 2x2y4
= x4y2 + x3y3 – 2x2y4

Question 24.
(x3 – 2x2 + 5x-7) (2x-3)
Solution:
(x3 – 2x2 + 5x – 7) (2x – 3)
= (2x – 3) (x3 – 2x2 + 5x – 7)
= 2x (x3 – 2x2 + 5x – 7) -3 (x3 – 2x2 + 5x – 7)
= 2x x x3 – 2x x 2x2 + 2x x 5x – 2x x 7 -3 x x3 – 3 x (-2x2) – 3 x 5x – 3 x (-7)
= 2x4-4x3 + 10x2– 14x-3x3 + 6x2– 15x + 21
= 2x4 – 4x3 – 3x3 + 10x2 + 6x2– 14x- 15x + 21
= 2x4-7x3 + 16x2-29x+ 21

Question 25.
(5x + 3) (x – 1) (3x – 2)
Solution:
(5x + 3) (x – 1) (3x – 2)
= (5x + 3) [x (3x – 2) -1 (3x – 2)]
= (5x + 3) [3x2 – 2x – 3x + 2]
= (5x + 3) [3x2 – 5x + 2]
= 5x (3x2 – 5x + 2) + 3 (3x2 – 5x + 2)
= (5x x 3x2 – 5x x Sx + 5x x 2)+ [3 x 3x2 + 3 x (-5x) + 3×2]
= 15x3 – 25x2 + 10x + 9x2 – 15x + 6
= 15x3 – 25x2 + 9x2 + 10x – 15x + 6
= 15x3 – 16x2 – 5x + 6

Question 26.
(5-x) (6-5x) (2-x)
Solution:
(5-x) (6-5x) (2-x)
= [5 (6 – 5x) -x (6 – 5x)] (2 – x)
= [30 – 2$x – 6x + 5x2] (2 – x)
= (30 – 3 1x + 5x2) (2-x)
= 2 (30 – 31x + 5x2) – x (30 – 31x + 5x2)
= 60 – 62x + 10x2 – 30x + 3 1x2 – 5x3
= 60 – 62x – 30x + 10x2 + 3 1x2 – 5x3
= 60 – 92x + 41x2 – 5x3

Question 27.
(2x2 + 3x – 5) (3x2 – 5x + 4)
Solution:
(2x2 + 3x – 5) (3x2 – 5x + 4)
= 2x2 (3x2 – 5x + 4) + 3x (3x2 – 5x + 4) -5 (3x2 – 5x + 4)
= 2x2 x 3x2 – 2x2 x 5x + 2x2 x 4 + 3x x 3x2 – 3x x 5x + 3x x 4 – 5 x 3x2 – 5 (-5x) -5×4
= 6x4 – 10x3 + 8x2 + 9x3 – 15x2 + 12x – 15x2 + 25x-20
= 6x4 – 10x3 + 9x3 + 8x2 – 15x2 – 15x2 + 12x + 25x – 20
= 6x4 – x3 – 22x2 + 37x – 20

Question 28.
(3x – 2) (2x – 3) + (5x – 3) (x + 1)
Solution:
(3x – 2) (2x – 3) + (5x – 3) (x + 1)
= 3x (2x – 3) -2 (2x – 3) + 5x (x + 1) – 3 (x + 1)
= 6x2 – 9x – 4x + 6 + 5x2 + 5x – 3x – 3
= 6x2 + 5x2 – 9x – 4x + 5x – 3x + 6 – 3
= 11x2– 11x + 3

Question 29.
(5x – 3) (x + 2) – (2x + 5) (4x – 3)
Solution:
(5x – 3) (x + 2) – (2x + 5) (4x – 3)
= [5x (x + 2) -3 (x + 2)] – [2x (4x – 3) + 5 (4x – 3)]
= [5x2 + 1 0x – 3x – 6] – [8x2 – 6x + 20x -15]
= (5x2 + 7x – 6) – (8x2 + 14x – 15)
= 5x2 + lx – 6 – 8x2 – 14x + 15
= 5x2 – 8x2 + 7x – 14x – 6 + 15
= -3x2 – 7x + 9

Question 30.
(3x + 2y) (4x + 3y) – (2x – y) (7x – 3y)
Solution:
(3x + 2y) (4x + 3y) – (2x – y) (7x – 3y)
= [3x (4x + 3y) + 2y (4x + 3y)]-[2x (7x-3y)-y(7x-3y)]
= (12x2 + 9xy + 8xy + 6y2) – (14x2 – 6xy – 7xy + 3y2)
= (12x2 + 17xy + 6y2) – (14x2 – 13xy + 3y2)
= 12x2 + 17xy + 6y2 – 14x2 + 13xy – 3y2
= 12x2 – 14x2 + 17xy + 13xy + 6y2 – 3y2
= -2x2 + 30xy + 3y2
= -2x2 + 3y2 + 30xy

Question 31.
(x2-3x + 2) (5x- 2) – (3x2 + 4x-5) (2x- 1)
Solution:
(x2-3x + 2) (5x- 2) – (3x2 + 4x-5) (2x- 1)
= [5x (x2 – 3x + 2) -2 (x2 – 3x + 2)] – [2x (3x2 + 4x – 5) -1 (3x2 + 4x – 5)]
= [5x3 – 15x2 + 10x – 2x2 + 6x – 4] – [6x3 + 8x2 – 10x – 3x2 – 4x + 5]
= [5x3 – 15x2 – 2x2 + 10xc + 6x – 4] – [6x3 + 8x2 – 3x2 – 10x – 4x + 5]
= (5x3 – 17x2 + 16x-4) – (6x3 + 5x2 – 14x + 5)
= 5x3 – 17x2 + 16x – 4 – 6x3 – 5x2 + 14x – 5
= 5x3 – 6x3 – 17x2 – 5x2 + 16x + 14x – 4 – 5
= -x3 – 22x2 + 30x – 9

Question 32.
x3 – 2x2 + 3x – 4) (x – 1) – (2x – 3) (x2 – x + 1)
Solution:
(x3 – 2x2 + 3x – 4) (x – 1) – (2x – 3) (x2 – x + 1)
= [x (x3 – 2x2 + 3x – 4) – 1 (x3 – 2x2 + 3x – 4)] – [2x (x2 – x + 1) – 3 (x2 – x + 1)]
= [x4 – 2x3 + 3x2 – 4x – x3 + 2x2 – 3x + 4] [2x3 – 2x2 + 2x – 3x2 + 3x – 3]
= (x4 – 2x3 – x3 + 3x2 + 2x2 – 4x – 3x + 4) (2x3 – 2x2 – 3x2 + 2x + 3x – 3)
= (x4 – 3x3 + 5x2 – 7x + 4) – (2x3 – 5x2 + 5x – 3)
= x4 – 3x3 + 5x2 – 7x + 4 – 2x3 + 5x2 – 5x + 3
= x4 – 3x3 – 2x3 + 5x2 + 5x2 – 7x – 5x + 4 + 3
= x4 – 5x3 + 10x2 – 12x + 7

Hope given RD Sharma Class 8 Solutions Chapter 6 Algebraic Expressions and Identities Ex 6.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7E

RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7E

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 7 Decimals Ex 7E.

Other Exercises

Question 1.
Solution:
(c) \(\\ \frac { 7 }{ 10 } \) = 0.7

Question 2.
Solution:
(d) \(\\ \frac { 5 }{ 100 } \) = .05

Question 3.
Solution:
(b) \(\\ \frac { 9 }{ 1000 } \) = 0.009

Question 4.
Solution:
(a) \(\\ \frac { 16 }{ 1000 } \) = 0.016

Question 5.
Solution:
(c) \(\\ \frac { 134 }{ 1000 } \) = 0.134

Question 6.
Solution:
(a) \(2 \frac { 17 }{ 100 } \) = 2.17

Question 7.
Solution:
(b) \(4 \frac { 3 }{ 1000 } \) = 4.03

Question 8.
Solution:
(b) 6.25 = \(6 \frac { 25 }{ 100 } \) = \(6 \frac { 1 }{ 4 } \)

Question 9.
Solution:
(b) \(\\ \frac { 6 }{ 25 } \)
= \(\\ \frac { 6\times 4 }{ 25\times 4 } \)
= \(\\ \frac { 24 }{ 100 } \)
= 0.24

Question 10.
Solution:
(c) \(4 \frac { 7 }{ 8 } \) = \(\\ \frac { 39 }{ 8 } \) = 4.875

Question 11.
Solution:
(a) 24.8 = \(24 \frac { 8 }{ 10 } \)
= \(24 \frac { 4 }{ 5 } \)

Question 12.
Solution:
(b) \(2 \frac { 1 }{ 25 } \)
= 2 + \(\\ \frac { 1 }{ 25 } \) x \(\\ \frac { 4 }{ 4 } \)
= 2 + \(\\ \frac { 4 }{ 100 } \)
= 2.04

Question 13.
Solution:
(c) 2 + \(\\ \frac { 3 }{ 10 } \) + \(\\ \frac { 4 }{ 100 } \)
= 2 + \(\\ \frac { 30 }{ 100 } \) + \(\\ \frac { 4 }{ 100 } \)
= 2.34

Question 14.
Solution:
(b) \(2 \frac { 6 }{ 100 } \)
= 2 + 0.06
= 2.06

Question 15.
Solution:
(c) \(\\ \frac { 4 }{ 100 } \) + \(\\ \frac { 7 }{ 10000 } \)
= 0.04 + 0.0007
= 0.0407

Question 16.
Solution:
(c) 2.06
= \(\left( 2\times 1 \right) +\left( 6\times \frac { 1 }{ 100 } \right) \)
= \(2+\frac { 6 }{ 100 } \)

Question 17.
Solution:
(d) Among 2.600, 2.006, 2.660,2.080, 2.660 is the largest.

Question 18.
Solution:
(b) 2.002 < 2.020 < 2.200 < 2.222 is the correct.

Question 19.
Solution:
(a) 2.1 = 2.100 and 2.005
2.100 > 2.055
=> 2.1 > 2.055

Question 20.
Solution:
(b) 1cm = \(\\ \frac { 1 }{ 100 } \) m
= 0.01

Question 21.
Solution:
(b) 2 m 5 cm = 2.05 m

Question 22.
Solution:
(c) 2 kg 8 g = 2 + 0.008 = 2.008

Question 23.
Solution:
(b) 2 kg 56 g = 2.056 kg
(∵ 1000 g = 1 kg)

Question 24.
Solution:
(c) 2 km 35 m = 2.035 km
(∵ 1000 m = 1 km)

Question 25.
Solution:
(c) ∵ 0.4 + 0.004 + 4.4
= 4.804

Question 26.
Solution:
(a) ∵ 3.5 + 4.05 – 6.005
= 3.500 + 4.050 – 6.005
= 7.550 – 6.005
= 1.545

Question 27.
Solution:
(b) ∵6.3 – 2.8 = 3.5

Question 28.
Solution:
(c) ∵ 5.01 – 3.6 = 5.01 – 3.60
= 1.41

Question 29.
Solution:
(a) ∵ 2 – 0.7 = 2.0 – 0.7 = 1.3

Question 30.
Solution:
(a) ∵ 1.1 – 0.3
= 0.8

Hope given RS Aggarwal Solutions Class 6 Chapter 7 Decimals Ex 7E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D

RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 7 Decimals Ex 7D.

Other Exercises

Question 1.
Solution:
27.86 from 53.74
= 53.74 – 27.86
= 25.88 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q1.1

Question 2.
Solution:
64.98 from 103.87
103.87 – 64.98
= 38.89 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q2.1

Question 3.
Solution:
59.63 from 92.4
92.40 – 59.63
= 32.77 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q3.1

Question 4.
Solution:
56.8 from 204
204.0 – 56.8
= 147.2 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q4.1

Question 5.
Solution:
127.38 from 216.2
216.20 – 127.38
= 88.82 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q5.1

Question 6.
Solution:
39.875 from 70.68
70.680 – 39.875
= 30.805 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q6.1

Question 7.
Solution:
523.120 – 348.237
= 174.883 Ans
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q7.1

Question 8.
Solution:
600.000 – 458.573
= 141.427 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q8.1

Question 9.
Solution:
206.321 – 149.456
= 56.865 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q9.1

Question 10.
Solution:
3.400 – 0.612
= 2.788 Ans
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q10.1

Question 11.
Solution:
Converting them in like decimals
37.600 + 72.850 – 58.678 – 6.090
= (37.600 + 72.850) – (58.678 + 6.090)
= 110.450 – 64.768
= 45.682
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q11.1

Question 12.
Solution:
75.3 – 104.645 + 178.96 – 47.9
= 75.300 – 104.645 + 178.960 – 47.900
(Converting into like decimals)
= 75.300 + 178.960 – 104.645 – 47.900
= (75.300 + 178.960) – (104.645 + 47.900)
= 254.260 – 152.545
= 101.715 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q12.1

Question 13.
Solution:
213.4 – 56.84 – 11.87 – 16.087
= 213.400 – 56.840 – 11.870 – 16.087
(Converting into like decimals)
= 213.400 – (56.840 + 11.870 + 16.087)
= 213.400 – 84.797
= 128.603 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q13.1

Question 14.
Solution: 76.3 . 7.666 . 6.77
= 76.300 – 7.666 – 6.770
(Converting into like decimals)
= 76.300 – 14.436
= 61.864 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q14.1

Question 15.
Solution:
In order to get the required number, we have to subtract 74.5 from 91.
Required number = 91 – 74.5
= 91.0 – 74.5
= 16.5 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q15.1

Question 16.
Solution:
In order to get the required numbers, we have to subtract 0.862 from 7.3.
Required number = 7.3 – 0.862
= 7.300 – 0.862
= 6.438 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q16.1

Question 17.
Solution:
In order to get the required number, we have to subtract 23.754 from 50
Required number = 50 – 23.754
= 50.000 – 23.754
= 26.246 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q17.1

Question 18.
Solution:
In order to get the required number, we should subtract 27.84 from 84.5
Required number = 84.5 – 27.84
= 84.50 – 27.84
= 56.66 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q18.1

Question 19.
Solution:
Weight of Neelam’s bag = 6 kg 80 g
Weight of Garima bag = 5 kg 265 g
Difference in their weights = 6 kg 80 g – 5 kg 265 g
= 6.080 kg – 5.265 kg
= 0.815 kg
= 815 g
Neelam’s bag is heavier by 815 g Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q19.1

Question 20.
Solution:
Cost of a notebook = Rs. 19.75
Cost of a pencil = Rs. 3 .85
Cost of a pen = Rs. 8.35
Total cost = Rs. 19.75 + Rs. 3.85 + Rs. 8.35
= Rs. 31.95
Amount given to the bookshop = Rs. 50
Balance amount to get back = Rs. 50.00 – Rs. 31.95
= Rs. 18.05 Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q20.1

Question 21.
Solution:
Weight of fruits = 5 kg 75 g .
Weight of vegetables = 3 kg 465 kg
Total weight of both = 5 kg 75 g + 3 kg 465 g
= 5.075 kg + 3.465 kg
= 8.540 kg
Gross weight of bag with these things = 9 kg
Net weight of bag = 9.000 – 8.540
= 0.460 kg
= 460 g Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q21.1

Question 22.
Solution:
Total distance = 14 km
Distance covered by scooter = 10 km 65 m
Distance covered by bus = 3 km 75 m
Total distance covered by scooter and by bus = 10 km 65 m + 3 km 75 m
= 10.065 km + 3 075 m
= 13.140 km
Remaining distance covered by walking
= (14.000 – 13.140) km
= 0.860 km
= 860 m Ans.
RS Aggarwal Class 6 Solutions Chapter 7 Decimals Ex 7D Q22.1

Hope given RS Aggarwal Solutions Class 6 Chapter 7 Decimals Ex 7D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A

RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10A.

Other Exercises

Question 1.
Solution:
(i) 24 to 56
= \(\\ \frac { 24 }{ 56 } \)
= \(\frac { 24\div 8 }{ 56\div 8 } \)
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q1.1
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q1.2
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q1.3

Question 2.
Solution:
(i) 36 : 90
= \(\\ \frac { 36 }{ 90 } \)
= \(\frac { 36\div 18 }{ 90\div 18 } \)
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q2.1
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q2.2
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q2.3
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q2.4
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q2.5

Question 3.
Solution:
(i) The given ratio = Rs. 6.30 : Rs. 16.80
= \(\\ \frac { Rs.6.30 }{ Rs.16.80 } \)
= \(\\ \frac { 630 }{ 1680 } \)
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q3.1
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q3.2
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q3.3
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q3.4

Question 4.
Solution:
Earning of Sahai = Rs. 16800
and of his wife = Rs. 10500
Then total income = Rs. 16800 + 10500
= Rs. 27300
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q4.1
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q4.2

Question 5.
Solution:
Rohit monthly earnings = Rs. 15300
and his savings = Rs. 1224
So, his expenditure = Rs. 15300 – 1224
= Rs. 14076
Now,
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q5.1
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q5.2

Question 6.
Solution:
Let the number of male and female workers in the mill be 5x and 3x respectively. Then,
5x = 115
=> \(\\ \frac { 5x }{ 5 } \) = \(\\ \frac { 115 }{ 5 } \)
(Dividing both sides by 5)
=> x = 23
Number of female workers in the mill
= 3x
= 3 x 23 = 69.

Question 7.
Solution:
Let the number of boys and girls in the school be 9x and 5x respectively.
According to the question,
9x + 5x = 44
=> 14x = 448
=> \(\\ \frac { 14x }{ 14 } \) = \(\\ \frac { 448 }{ 14 } \)
(Dividing both sides by 14)
=> x = 32.
Number of girls =5x
= 5 x 32
= 160

Question 8.
Solution:
Total amount = Rs. 1575
Ratio in Kamal and Madhu’s share = 7 : 2
Sum of ratios = 7 + 2 = 9
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q8.1

Question 9.
Solution:
Total amount = Rs. 3450
Ratio in A, B and C shares = 3 : 5 : 7
Sum of share = 3 + 5 + 7 = 15
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q9.1

Question 10.
Solution:
Let the numbers be 11x and 12x.
Then. 11x + 12x = 460
=> 23x = 460
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q10.1

Question 11.
Solution:
Length of line segment = 35 cm
Ratio = 4 : 3
Sum of ratio = 4 + 3 = 7
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q11.1

Question 12.
Solution:
Total bulbs produced per day = 630
Out of every 10 bulbs, defective bulb = 1
Out of every 10 bulbs, lighting bulbs = 10 – 1 = 9
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q12.1

Question 13.
Solution:
Price of 20 pencils = Rs. 96
(1 score = 20 pencils)
Price of 1 pencil = Rs. (96 ÷ 20)
= Rs. 4.80
Price of 12 ball pens = Rs. 50.40
(1 dozen = 12)
Price of 1 ball pen = Rs. (50.40 ÷ 12)
= Rs. 4.20.
Ratio of the price of a pencil to that of a ball pen = Rs. 4.80 : Rs. 4.20
= 480 paise : 420 paise
= 480 : 420
= 48 : 42
= 8 : 7.
Required ratio = 8 : 7.

Question 14.
Solution:
It is given that the ratio of the length of a field to its width is 5 : 3.
If the width of the field is 3 metres then length = 5 metres.
If the width of the field is 1 metres than length = \(\\ \frac { 5 }{ 3 } \) metres.
If the width of the field is 42 metres then length
= \(\\ \frac { 5 }{ 3 } \) x 42 metres
= 5 x 14 metres
= 70 metres.

Question 15.
Solution:
Ratio in income and savings of a family = 11 : 2
But Total savings = Rs. 1520
Let income = x
11 : 2 = x : 1520
=> x = \(\\ \frac { 11\times 1520 }{ 2 } \) = 11 x 760
= Rs 8360
Expenditure = total income – savings
= Rs 8360 – 1520
= Rs 6840

Question 16.
Solution:
Ratio in income and expenditure = 7 : 6
Total income = Rs. 14000
Let expenditure = x, then
7 : 6 :: 14000 : x
=>x = \(\\ \frac { 6\times 14000 }{ 7 } \) = Rs. 12000
Savings = Total income – Expenditure
= Rs. 14000 – 12000
= Rs. 2000

Question 17.
Solution:
It is given that the ratio of zinc and copper in an alloy is 7 : 9.
If the weight of zinc in the alloy is 7 kg then the weight of copper in the alloy is 9 kg.
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q17.1

Question 18.
Solution:
A bus covers in 2 hours = 128 km
128 It will cover in 1 hour = \(\\ \frac { 128 }{ 2 } \) = 64 km
A train cover in 3 hours = 240 km
It will cover in 1 hour = \(\\ \frac { 240 }{ 3 } \)
= 80 km
Ratio in their speeds = 64: 80
= 4 : 5
{Dividing by 16, the LCM of 64, 80}

Question 19.
Solution:
(i) (3 : 4) or (9 : 16)
LCM of 4, 16 = 16
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q18.1
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q18.2
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q18.3
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q18.4

Question 20.
Solution:
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q20.1
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q20.2
RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10A Q20.3

 

Hope given RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

CA Foundation Business Economics Study Material – Meaning of Production

CA Foundation Business Economics Study Material Chapter 3 Theory of Production and Cost – Meaning of Production

Meaning of Production

  • Production is one of the important economic activity that takes place in any economy apart from consumption and investments.
  • An individual firm is the micro-economic unit which undertake the production of goods and services.
  • A firm’s survival depends upon whether it is able to achieve optimum efficiency in production by minimizing the cost of production.
  • Production is the transformation of resources into goods and services. In other words, production is the act of transformation of INPUTS into OUTPUT which satisfies the wants of some people.
    E.g.- Inputs of sugarcane, capital and labour are used to produce SUGAR.
    Production also includes production of SERVICES like those of lawyers, teachers, doctors, etc.
  • The amount of goods and services that an economy is able to produce determines whether it is rich or poor. A country like U.S.A. is a rich country as its production level is high.
  • Man cannot create or destroy matter.
  • In Economics, the term production means creation of economic utilities in the matter i.e. in the things that already exist.
  • Thus, production means creation of those goods and services which have economic utilities i.e. exchange value.
  • According to James Bates and J.R. Parkinson, “Production is the organized activity of transforming resources into finished products in the form of goods and services; and the objective of production is to satisfy the demand of such transformed resources.”
  • Professor J. R. Hicks has defined production “as any activity whether physical or mental, which is directed to the satisfaction of other people’s wants through exchange.”
  • The definition indicates that the term production covers the whole process from creation of utilities till the satisfaction of human wants.

Utilities may be created or added in many ways, such as :-

1. Form Utility

  • It is created by changing the form of raw materials into finished goods for man’s use.
  • E.g. converting raw cotton into cotton fabric.
  • Form utility is created by manufacturing industries.

2. Place Utility

  • It is created by transporting goods from one place to another.
  • E.g. when goods are taken from factory to marketplace, place utility is created.
  • Transport services are involved in creation of place utility.

3. Time Utility

  • It is created by making things available when they are required.
  • E.g. Banks create time utility by granting overdraft facilities.

4. Service Utility (Personal Utility)

  • It is created by providing personal services to the customers by professionals likes lawyers, doctors, bankers, shopkeepers, teachers, transporters, etc