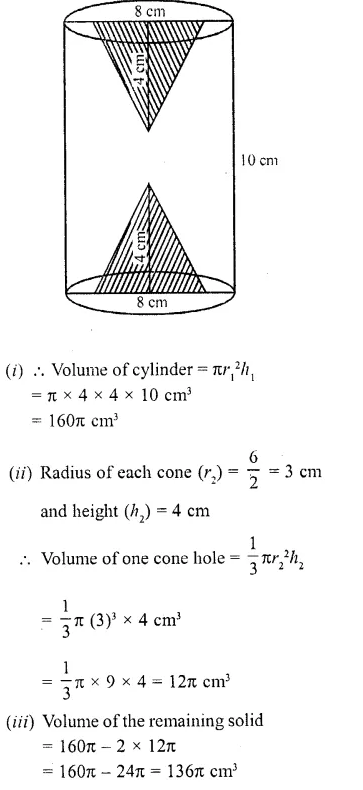
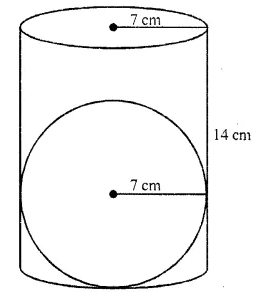
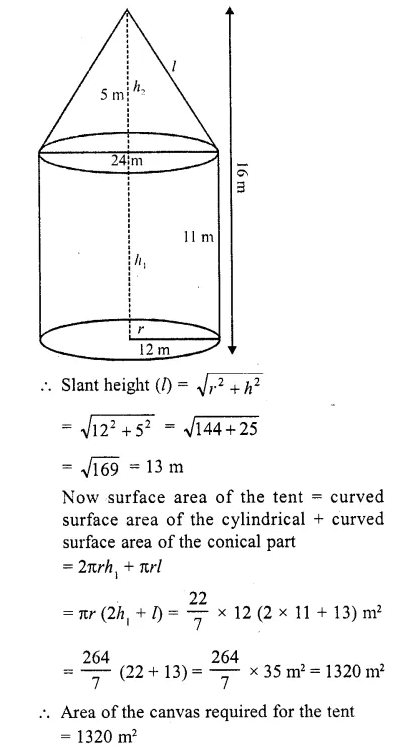
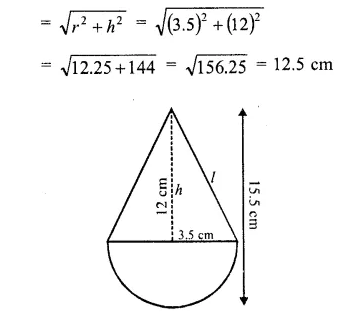
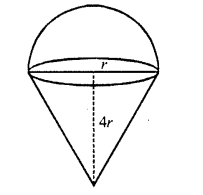
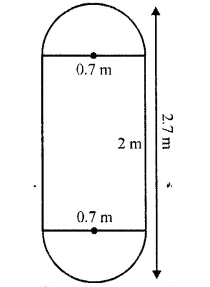
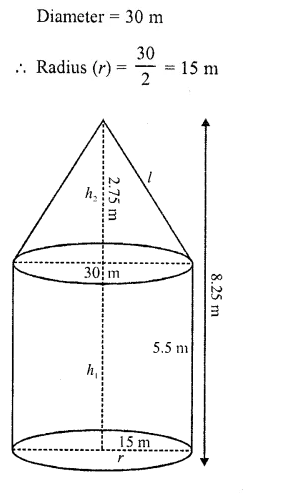
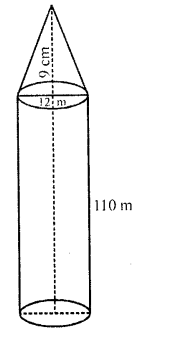
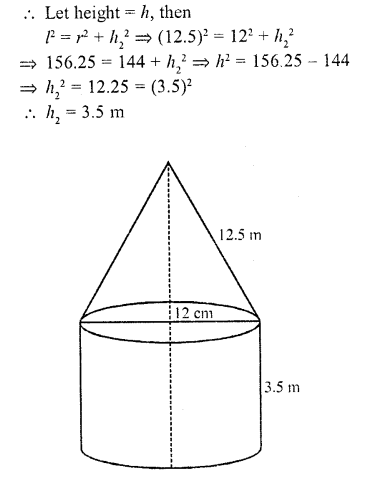
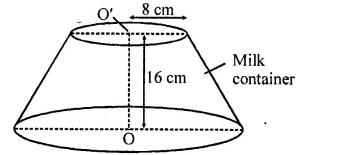
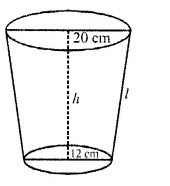
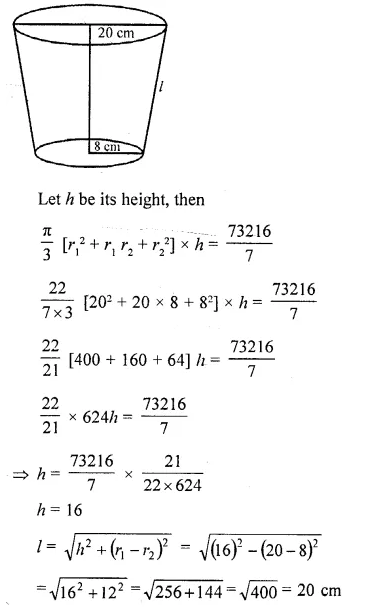
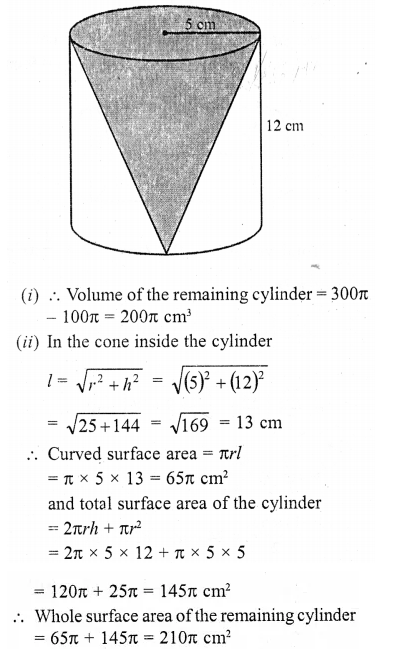
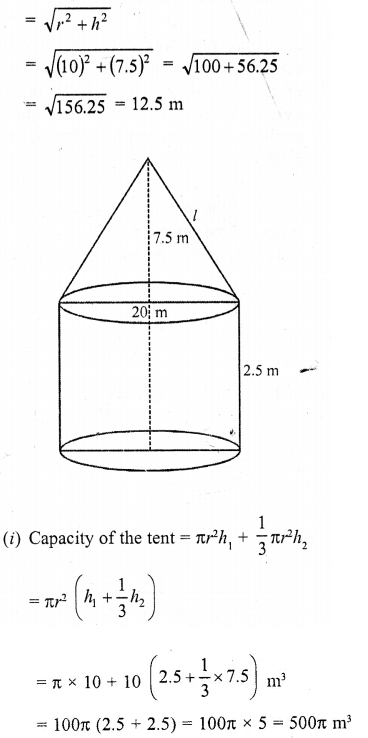
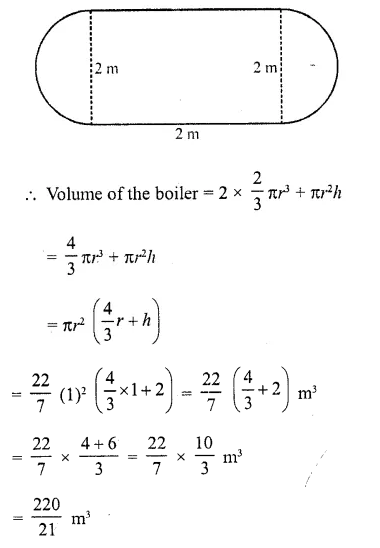
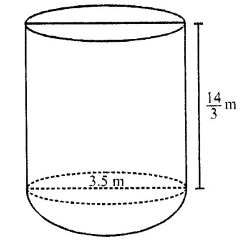
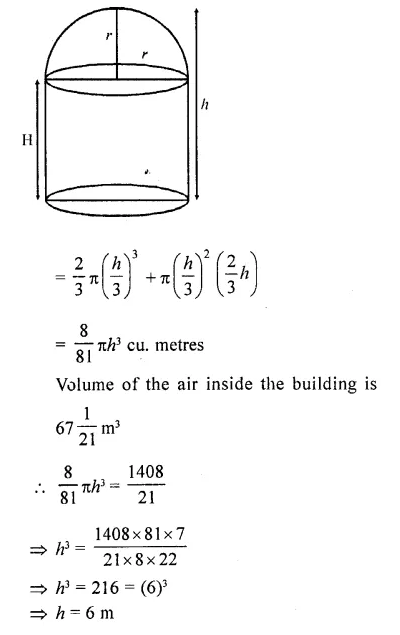
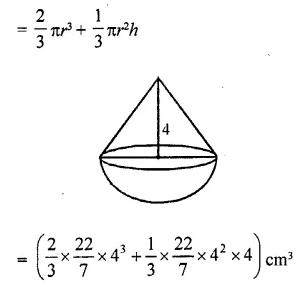
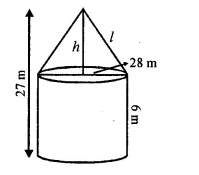
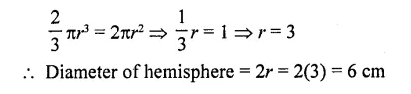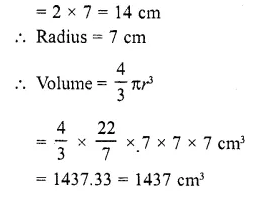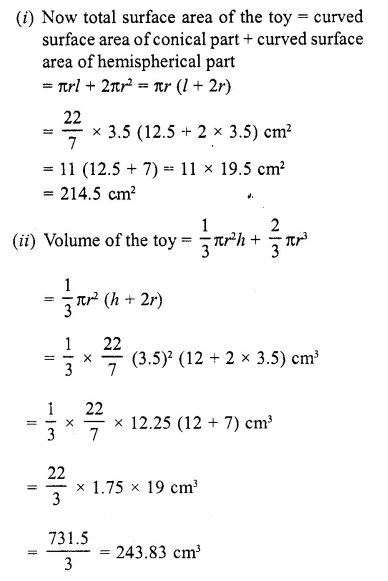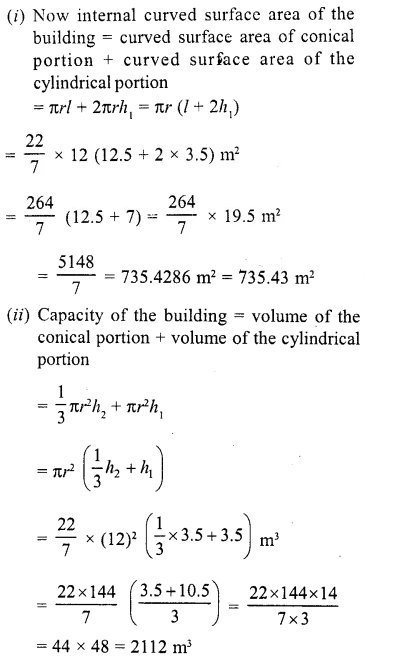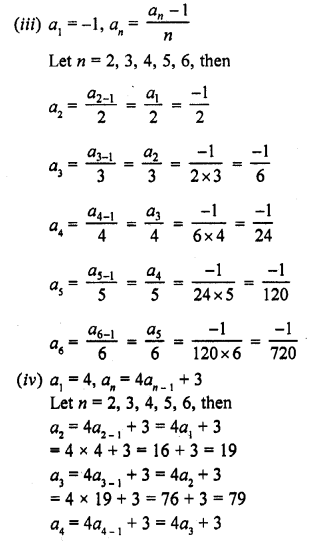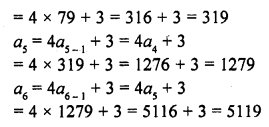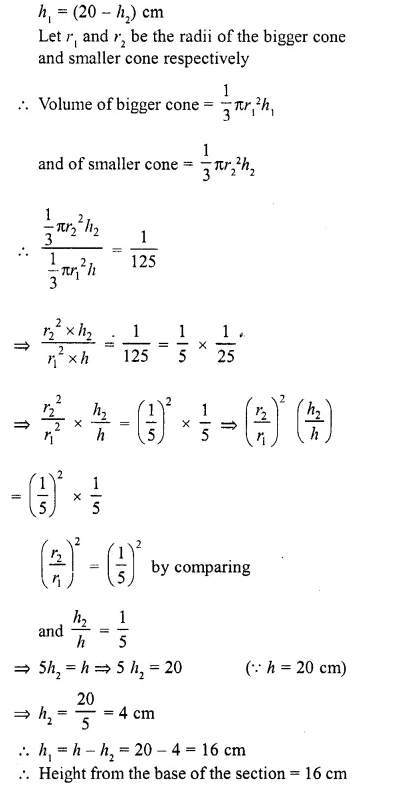CA Foundation Business Economics Study Material – Demand Forecasting

CA Foundation Business Economics Study Material Chapter 2 Theory of Demand and Supply – Demand Forecasting

Demand Forecasting

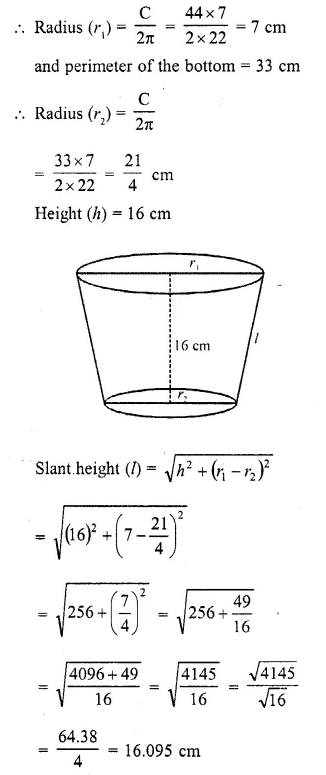
Meaning:

  • Demand forecasting is an estimate of the future market demand for a product. The process of forecasting is based on reliable statistical data of past and present behaviour, trends, etc.
  • Demand forecasting cannot be hundred per cent correct. But, it gives a reliable estimates of the possible outcome with a reasonable accuracy.
  • Demand forecasting may be at international level or local level depending upon area of operation, cost, time, etc.

Usefulness:

Demand forecasting is an important function, of managers as it reduces uncertainty of environment in which DECISIONS are made. Further, it helps in PLANNING for future level of production. Its significance can be stated as follows:

  1. Production Planning: Demand forecasting is a pre-requisite for planning of production in a firm. Expansion of production capacity depends upon likely demand for its output. Otherwise, there may be overproduction or underproduction leading to losses.
  2. Sales Forecasting: Sales forecasting depends upon demand forecasting. Promotional efforts of the firm like advertisements, suitable pricing etc. should be based on demand forecasting.
  3. Control of Business: Demand forecast provide information for budgetary planning and cost control in functional area of finance and accounting.
  4. Inventory Control: Demand forecasting helps in exercising satisfactory control of business inventories like raw-materials, intermediate goods, semi-finished goods, spare parts, etc. Estimates of future requirement of inventories is to be done regularly and it can be known from demand forecasts.
  5. Capital Investments: Capital investments yield returns over many years in future. Decision about investment is to be taken by comparing rate of return on capital investment and current rate of interest. Demand forecasting helps in taking investment decisions.

Types of forecasts:

Macro-level forecasting deals with the general economic environment prevailing in the economy as measured by the Index of Industrial Production (IIP), national income and general level of employment, government expenditure, consumption level, consumers spending habits, etc.

  1. Industry-level forecasting refers to forecasting the demand of a good of a particular industry as a whole.
    E.g.- Demand for two-wheelers in India.
  2. Firm-level forecasting refers to forecasting the demand of a good of a particular firm.
    E.g.- Bajaj motor cycle.

Based on time period, demand forecasting may be-

  1. Short-term demand forecasting normally relates to a period not exceeding a year. It is also called as ‘operating forecast’. It is useful for estimating stock requirement, providing working capital, etc.
  2. Long-term demand forecasting may cover one to five years, depending on the nature of the firm. It provides information for taking decisions like expansion of plant capacity, man-power planning, long-term financial planning, etc.

Demand Distinctions

1. Producer’s goods and Consumer’s Goods

  • The goods which are used for the production of other goods are called producer’s goods. E.g. Machines
  • The goods which are used for final consumption are called consumer’s goods. E.g. readymade clothes, toothpaste, soap, house etc.

2. Durable goods and Non-durable goods

  • Goods can be further divided into durable and non-durable goods.
  • Durable goods are those which can be consumed more than once and yield utility over a period of time.
    – Producer’s Durable Goods – E.g.- Building, Plant, Machinery etc.
    – Consumer’s Durable Goods – E.g.- Cars, TV, Refrigerators, etc.
  • Non-durable goods are those which cannot be consumed more than once. These will meet only the current demand.
    – Producer’s Non-durable Goods – E.g.- raw material, fuel, power, etc.
    – Consumer’s Non-durable Goods – E.g.- milk, bread, etc.

3. Derived demand and Autonomous demand

  • The demand for a commodity is said to be derived when its demand depends on the demand for some other commodity. In other words, it is the demand which has been derived from the demand for some other commodity called “parent product”.
    E.g. The demand for bricks, cement, steel, sand, etc. is derived demand because their demand depends on the demand for houses. Producer goods and complementary goods have derived demand.
  • When the demand of a commodity is independent of the demand for other commodity, then it is called autonomous demand.

4. Industry demand and Company demand

  • The total demand of a commodity of a particular industry is called industry demand.
    E.g. the total demand for shoes in the country.
  • The demand for the commodity of a particular company is called company demand.
    E.g. shoes produced by BATA.

5. Short-run demand and long-run demand

  • When the demand respond immediately to price changes, income changes etc. is referred as short-run demand.
  • When the demand still exist as a result of changes in pricing, sales promotion, quality improvement etc. after enough time is allowed to let the market adjust to the new situation is called long-run demand.

Factors affecting demands for non-durable goods
The factors which affects the demand of NON-DURABLE CONSUMER GOODS are as follows:-

  • Disposable Income: The income left with a person after paying direct taxes and other deductions is called as disposable income. Other things being equal, more the disposable income of the household, more is its demand for goods and vice versa.
  • Price: The demand for a commodity depends upon its price and the prices of its substitutes y and complements. The demand for a commodity is inversely related to its own price and the price of its complements. The demand for a commodity is positively related to its substitutes.
  • Demography: This involves the characteristics of the populations, human as well as non human which use the given product. E.g. – If forecast about the demand for toys is to be made, we will have to estimate the number and characteristics of children whose parents can afford toys.

Factors affecting the demand for consumer durable goods

  • Long time use or replacement: For how long a consumer can use a good depends on the factors like his status, prestige attached to good, his level of money income, etc. Replacement of a good depends upon the factors like the wear and tear rate, the rate of obsolescence, etc.
  • Special Facilities: Some goods need special facilities for their use. E.g. Roads for cars, electricity for T.V., refrigerators etc. The expansion of such facilities expands the demand for such goods.
  • Joint use of a good by household: As consumer durables are used by more than one person, the decision to purchase may be influenced by family characteristics like size of family, age and sex consumption.
  • Price and Credit facilities: Demand for consumer durables is very much influenced by their prices and credit facilities like hire purchase, low interest rates, etc. available to buy them. More the easy credit facilities higher is the demand for goods like two wheelers, cars TVs. etc.

Factors affecting the demand for producer goods

  • The demand for producer or capital goods is a derived demand. It is derived from the demand of consumer goods they produce.
  • The forecasting of a capital good depends upon the following factors:
    – Increase in the price of substitutable factor increases the demand for capital goods.
    – The existing stock of the capital goods.
    – Technology advancement leading to reduced cost of production.
    – Prevailing rates of interest etc.

Methods of Demand Forecasting

There is no easy method to predict the future with certainty. The firm has to apply a proper mix of methods of forecasting to predict the future demand for a product. The various methods of demand forecasting are as follows:

1. Survey of Buyer’s intentions: In this method, customers are asked what they are planning to buy for the forthcoming time period usually a year.

This method involve use of conducting direct interviews or mailing questionnaire asking customers about their intentions or plans to buy the product.

The survey may be conducted by any of the following methods:

  • Complete Enumeration where all potential customers of a product are interviewed about what they are planning or intending to buy in future. It is cumbersome, costly and time consuming method.
  • Sample Survey where only a few customers are selected and interviewed about their future plans. It is less cumbersome and less costly method.
  • End-use method or Input-output method where the bulk of good is made for industrial manufactures who usually have definite future plans.

This method is useful for short-term forecasts.
In this method burden of forecasting is put on the customers.

2. Collective opinion Method: The method is also known as sales force opinion method or grass roots approach.

  • Under this method, salesmen are asked to estimate expectations of sales in their territories. Salesmen are considered to be the nearest persons to the customers retailers and wholesalers and have good knowledge and information about the future demand trend.
  • The estimates of all the sales-force is collected are examined in the light of proposed changes in selling price, product design, expected competition, etc. and also factors like purchasing power, employment, population, etc.
  • This method is based on first hand knowledge of the salesmen. However, its main drawback is that it is subjective. Its accuracy depends on the intelligence, vision and his ability to foresee the influence of many unknown factors.

3. Expert Opinion Method (Delphi Method): Under this method of demand forecasting views of specialists/experts and consultants are sought to estimate the demand in future. These experts may be of the firm itself like the executives and sales managers or consultant firms who are professionally trained for forecasting demand.

  • The Delphi technique, developed by OLAF HEMLER at the Rand Corporation of the
    U.S.A. is used to get the opinion of a number of experts about future demand.
  • Experts are provided with information and opinion feedbacks of other experts at different rounds and are repeatedly questioned for their opinion and comments till consensus emerges.
  • It is a time saving method.

4. Statistical Method: Statistical method have proved to be very useful in demand forecasting. Statistical methods are superior, more scientific, reliable and free from subjectively. The important statistical methods of demand forecasting are:

  • Trend Projection Method: The method is also known as Classical Method. It is considered as a ‘naive’ approach to demand forecasting.
    • Under this, data on sales over a period of time is chronologically arranged to get a ‘time series’. The time series shows the past sales pattern. It is assumed that the past sales pattern will continue in the future also. The techniques of trend projection based on, time series data are Graphical Method and Fitting trend equation or Least Square Method.
  • Graphical Method: This is the simplest technique to determine the trend.
    • Under this method, all values of sales for different years are plotted and free hand curve is drawn passing through as many points as possible. The direction of the free hand curve shows the trend.
    • The main drawback of this method is that it may show trend but not measure it.
  • Fitting Trend Equation/Least Square Method: This method is based on the assumption that the past rate of change will continue in the future.
    • It is a mathematical procedure for fitting a time to a set of observed data points in such a way that the sum of the squared deviation between the calculated and observed values is minimized.
    • This method is popular because it is simple and inexpensive.
  • Regression Analysis: This is a very common method of forecasting demand.
  • Under this method, a quantitative relationship is established between quantity demanded (dependent variable) and the independent variables like income, price of good, price of related goods, etc. Based on this relationship, an estimate is made for future demand.
  • It can be expressed as follows-
    Y = a + b X
    Where
    X, Y are variables a, b are constants

5. Controlled Experiments: Under this method, an effort is made to vary certain determinants of demand like price, advertising, etc. and conduct the experiments assuming that the other factors remain constant.

  • The effect of demand determinants on sales can be assessed either by varying then in different markets or by varying over a period of time in the same market.
  • The responses of demand to such changes over a period of time are recorded and are used for estimating the future demand for the product.
  • This method is used less as it is expensive and time consuming.
  • This method is also called as market experiment method.

6. Barometric Method of forecasting: This method is based on the assumption that future can be predicted from certain events occurring in the present. We need not depend upon the past observations for demand forecasting.

There are economic ups and downs in an economy which indicate the turning points. There are many economic indicators like income, population, expenditure, investment, etc. which can be used to forecast demand. There are three types of economic indicators, viz.

  • Coincidental Indicators are those which move up and down simultaneously with aggregate economy. It measures the current economic activity. E.g.- rate of unemployment.
  • Leading Indicators reflect future change in the trend of aggregate economy.
  • Lagging Indicators reflect future changes in the trend of aggregate economic activities.

 

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS

Other Exercises

Question 1.
The radii of the bases of a cylinder and a cone are in the ratio 3 : 4 and their heights are in the ratio 2 : 3. What is the ratio of their volumes ?
Solution:
Radii of the bases of a cylinder and a cone = 3:4
and ratio in their heights = 2:3
Let r1, r2 be the radii and h1 and h2 be their heights
heights of the cylinder and cone respectively,
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 1

Question 2.
If the heights of two right circular cones are in the ratio 1 : 2 and the perimeters of their bases are in the ratio 3 : 4. What is the ratio of their volumes ?
Solution:
Ratio in the heights of two cones =1:2 and ratio in the perimeter of their bases = 3:4
Let r1, r2 be the radii of two cones and ht and h2 be their heights
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 2

Question 3.
If a cone and sphere have equal radii and equal volumes what is the ratio of the diameter of the sphere to the height of the cone ?
Solution:
Let r be the radius of a cone, then
radius of sphere = r
Let h be the height of cone
Now volume of cone = volume of sphere
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 3

Question 4.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. What is the ratio of their volumes?
Solution:
Let r and h be the radius and heights of a cone, a hemisphere and a cylinder
∴ Volume of cone =  \((\frac { 1 }{ 3 } )\) πr²h
Volume of hemisphere = \((\frac { 2 }{ 3 } )\) πr³
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 4

Question 5.
The radii of two cylinders are in the ratio 3 : 5 and their heights are in the ratio 2 : 3. What is the ratio of their curved surface areas ?
Solution:
Radii of two cylinders are in the ratio = 3:5
and ratio in their heights = 2:3
Let r1, r2 be the radii and h1, h2 be the heights of the two cylinders respectively, then
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 5

Question 6.
Two cubes have their volumes in the ratio 1 : 27. What is the ratio of their surface areas ?
Solution:
Ratio in the volumes of two cubes = 1 : 27
Let a1 and a2 be the sides of the two cubes respectively then volume of the first area = a1³
and volume of second cube = a2³
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 6

Question 7.
Two right circular cylinders of equal volumes have their heights in the ratio 1 : 2. What is the ratio of their radii ?
Solution:
Ratio the heights of two right circular cylinders = 1:2
Let r1,r2 be their radii and h1, h2 be their
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 7

Question 8.
If the volumes of two cones are in the ratio 1 : 4, and their diameters are in the ratio 4 : 5, then write the ratio of their weights.
Solution:
Volumes of two cones are in the ratio =1:4 and their diameter are in the ratio = 4:5
Let r1 and r2 be the radii and h1 ,h2 be their
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 8

Question 9.
A sphere and a cube have equal surface areas. What is the ratio of the volume of the sphere to that of the cube ?
Solution:
Surface areas of a sphere and a cube are equal
Let r be the radius of sphere and a be the edge of cube,
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 9

Question 10.
What is the ratio of the volume of a cube to that of a sphere which will fit inside it?
Solution:
A sphere is fit inside the cube
Side of a cube = diameter of sphere
Let a be the side of cube and r be the radius of the sphere, then
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 10

Question 11.
What is the ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height ?
Solution:
Diameters (or radii), and heights of a cylinder a cone and a sphere are equal,
Let r and h be the radius and height be the cone cylinder, cone and sphere respectively, thus their volumes will be
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 11

Question 12.
A sphere of maximum volume is cut-out from a solid hemisphere of radius r. What is the ratio of the volume of the hemisphere to that of the cut-out sphere?
Solution:
r is the radius of a hemisphere, then
the diameter of the sphere which is cut out of the hemisphere will be r
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 12

Question 13.
A metallic hemisphere is melted and recast in the shape of a cone with the same base radius R as that of the hemisphere. If H is the height of the cone, then write the value of \((\frac { H }{ R } )\).
Solution:
R is the radius of a hemisphere 2
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 13

Question 14.
A right circular cone and a right circular cylinder have equal base and equal height. If the radius of the base and height are in the ratio 5 : 12, write the ratio of the total surface area of the cylinder to that of the cone.
Solution:
Radius and height of a cone and a cylinder be r and h respectively
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 14

Question 15.
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes ?
Solution:
Let r and h be the radii and heights of the cylinder cone and hemisphere respectively, then
Volume of cylinder = πr²h
Volume of cone = \((\frac { 1 }{ 3 } )\) πr²h
Volume of hemisphere = \((\frac { 2 }{ 3 } )\) πr³
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 15

Question 16.
The radii of two cones are in the ratio 2 : 1 and their volumes are equal. What is the ratio of their heights ?
Solution:
Radii of two cones are in the ratio = 2:1
Let r1, r2 be the radii of two cones and h1, h2 be their heights respectively,
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 16

Question 17.
Two cones have their heights in the ratio 1 : 3 and radii 3:1. What is the ratio of their volumes ?
Solution:
Ratio in heights of two cones = 1:3
and ratio in their ratio = 3:1
Let r1, r2 be their radii and h1, h2 be their
heights, then
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 17

Question 18.
A hemisphere and a cone have equal bases. If their heights are also equal, then what is the ratio of their curved surfaces ?
Solution:
Bases of a hemisphere and a cone are equal
and their heights are also equal
Let r and h be their radii and heights
respectively
∴ r = h1
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 18

Question 19.
If r1 and r2 denote the radii of the circular bases of the frustum of a cone such that r1 > r2 then write the ratio of the height of the cone of which the frustum is a part to the height of the frustum.
Solution:
r1 , r2 are the radii of the bases of a frustum and r1 > r2
Let h1 be the height of cone and h2 be the height of smaller cone
∴ Height of frustum = h1 – h2
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 19

Question 20.
If the slant height of the frustum of a cone is 6 cm and the perimeters of its circular bases are 24 cm and 12 cm respectively. What is the curved surface area of the frustum ?
Solution:
Slant height of a frustum (l) = 6 cm
Perimeter of upper base (P1) = 24 cm
and perimeter of lower base (P2) = 12 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 20

Question 21.
If the areas of circular bases of a frustum of a cone are 4 cm² and 9 cm² respectively and the height of the frustum is 12 cm. What is the volume of the frustum ?
Solution:
In a frustum,
Area of upper base (A1) = 4 cm²
and area of lower base (A2) = 9 cm²
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 21

Question 22.
The surface area of a sphere is 616 cm². Find its radius.
Solution:
Surface area of a sphere = 616 cm²
Let r be the radius, then
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 22

Question 23.
A cylinder and a cone are of the same base radius and of same height. Find the ratio of the value of the cylinder to that of the cone. [CBSE 2009]
Solution:
Let r be the radius of the base of the cylinder
small as of cone
and let height of the cylinder = h
Then height of cone = h
∴ Volume of cylinder =  πr²h
and volume of cone = \((\frac { 1 }{ 3 } )\)  πr²h
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 23

Question 24.
The slant height of the frustum of a cone is 5 cm. If the difference between the radii of its two circular ends is 4 cm, write the height of the frustum. [CBSE 2010]
Solution:
Slant height of frustum (l) = 5 cm
Difference between the upper and lower radii = 4 cm
Let h be height and upper radius r1 and lower radius = r2
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 24

Question 25.
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
Solution:
Volume of hemisphere = Surface area of hemisphere (given)
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS 25

Hope given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise

Other Exercises

Question 1.
A metallic sphere 1 dm in diameter is beaten into a circular sheet of uniform thickness equal to 1 mm. Find the radius of the sheet.
Solution:
Diameter of a sphere = 1 dm = 10 cm
∴  Radius (r) = \((\frac { 10 }{ 2 } )\) = 5 cm
Volume of metal used in the sphere = \((\frac { 4 }{ 3 } )\) πr³
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 1

Question 2.
Three solid spheres of radii 3,4 and 5 cm respectively are melted and converted into a single solid sphere. Find the radius of this sphere.
Solution:
Radius of first sphere (r1) = 3 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 2

Question 3.
A spherical shell of lead, whose external diameter is 18 cm, is melted and recast into a right circular cylinder, whose height is 8 cm and diameter 12 cm. Determine the internal diameter of the shell.
Solution:
Diameter of the cylinder = 12 cm
∴  Radius (r1) = \((\frac { 12 }{ 2 } )\) = 6 cm
Height (h) = 8 cm
∴ Volume = πr1²h = π(6)² x 8 cm³
= π x 36 x 8 = 288π cm³
Now volume of metal used in spherical shell = 288π cm
External diameter = 18 cm 18
∴  External radius (R) = \((\frac { 18 }{ 2 } )\) = 9 cm
Let r be the internal radius, then
Volume of the metal = \((\frac { 4 }{ 3 } )\) π (R³ – r³ )
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 3

Question 4.
A well with 10 m inside diameter is dug 8.4 m deep. Earth taken out of it is spread all around it to a width of 7.5 m to form an embankment. Find the height of the embankment.
Solution:
Diameter of two well = 10 m
∴ Radius (r) = \((\frac { 10 }{ 2 } )\) = 5 m
Depth (h) = 8.4 m
∴ Volume of earth dug out = πr²h
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 4

Question 5.
 In the middle of a rectangular field measuring 30 m x 20 m, a well of 7 m diameter and 10 m depth is dug. The earth so removed is evenly spread over the remaining part of the field. Find the height through which the level of the field is raised.
Solution:
Diameter of well = 7 m
∴ Radius (r) = \((\frac { 7 }{ 2 } )\) m
Depth (h) = 10 m
∴ Volume of earth dug out = πr²h
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 5

Question 6.
The inner and outer radii of a hollow cylinder are 15 cm and 20 cm, respectively. The cylinder is melted and recast into a solid cylinder of the same height. Find the radius of the base of new cylinder.
Solution:
Inner radius of hollow cylinder (r) = 15 cm
Outer radius (R) = 20 cm
Let h be the height of the hollow cylinder,
Then volume of metal used = πR (R² – r²)
= πh (20²- 15²) cm³
=  πh (400 – 225) cm³
= 175 πh cm³
Volume of the new cylinder = 175nh cm³
Height = h
Let R be the radius of new cylinder,
then πR²h = 175 πh
⇒ R²= 175
⇒ R = \(\sqrt { 175 } \)
= 13.2
∴ Radius = 13.2 cm

Question 7.
Two cylindrical vessels are filled with oil. Their radii are 15 cm, 12 cm and heights 20 cm, 16 cm respectively. Find the radius of a cylindrical vessel 21 cm in height, which will just contain the oil of the two given vessels.
Solution:
Radius of first cylinder (r1) = 15 cm
and radius of second cylinder (r2) = 12 cm
Height of the first cylinder (h1) = 20 cm
and height of second cylinder (h2) = 16 cm
∴ Volume of both of cylinders
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 6

Question 8.
A cylindrical bucket 28 cm in diameter and 72 cm high is full of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide. Find the height of the water level in the tank.
Solution:
Diameter of cylindrical bucket = 28 cm
∴ Radius (r) = \((\frac { 28 }{ 2 } )\) = 14 cm
Height (h) = 72 cm
∴ Volume of water filled in it = πr²h
= \((\frac { 22 }{ 7 } )\) x 14 x 14 x 72 cm³ = 44352 cm³
∴ Volume of water in rectangular tank = 44352 cm³
Length of tank (l) = 66 cm
and breadth (b) = 28 cm
Let h1 be its height
∴  Ibh1 = 44352
⇒  66 x 28 h1= 44352
⇒ h1 = \((\frac { 44352 }{ 66×28 } )\) = 24
∴Height of water in the tank = 24 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 7

Question 9.
A cubic cm of gold is drawn into a wire 0.1 mm in diameter, find the length of the wire.
Solution:
Volume of solid gold = 1 cm³
Diameter of cylinderical wire = 0.1 mm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 8

Question 10.
A well of diameter 3 m is dug 14 m deep. The earth taken out of it is spread evenly all around it to a width of 4 m to form an embankment. Find the height of the embankment.
Solution:
Diameter of the well = 3 m
Radius (r) = \((\frac { 3 }{ 2 } )\) m
Depth (h) = 14 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 9
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 10

Question 11.
A conical vessel whose internal radius is 10 cm and height 48 cm is full of water. Find the volume of water. If this water is poured into a cylindrical vessel with internal radius 20 cm, find the height to which the water level rises in it.
Solution:
Internal radius of the conical vessel (r1) = 10 cm
Height (h1) = 48 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 11

Question 12.
The vertical height of a conical tent is 42 dm and the diameter of its base is 5.4 m. Find the number of persons it can accommodate if each person is to be allowed 29.16 cubic dm.
Solution:
Vertical height of conical tent (h) = 42 dm
and diameter base (b) = 5.4 dm
∴ Radius (r) = \((\frac { 5.4 }{ 2 } )\) = 2.7 dm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 12

Question 13.
A right circular cylinder and a right circular cone have equal bases and equal heights. If their curved surfaces are in the ratio 8 : 5, determine the ratio of the radius of the base to the height of either of them.
Solution:
Let r and h be the radius and height of a circular cylinder and also of a cone, then curved surface area of the cylinder = 2πrh
and curved surface area of cone
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 13

Question 14.
A sphere of diameter 5 cm is dropped into a cylindrical vessel partly filled with water. The diameter of the base of the vessel is 10 cm. If the sphere is completely submerged, by how much will the level of water rise ?
Solution:
Diameter of sphere = 5 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 14
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 15

Question 15.
A spherical ball of iron has been melted – and made into smaller balls. If the radius of each smaller ball is one-fourth of the radius of the original one, how many such balls can be made ?
Solution:
Let the radius of larger ball = r
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 16

Question 16.
Find the depth of a cylindrical tank of radius 28 m, if its capacity is equal to that of a rectangular tank of size 28 m x 16 m x 11 m.
Solution:
Dimensions of a rectangular tank = 28m x 16m x 11m
∴ Volume = 28 x 16 x 11 m³ = 4928 m³
∴  Volume of cylindrical tank = 4928 m³
Radius of the cylindrical tank = 28 m
Let h be depth of the tank, then
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 17

Question 17.
A hemispherical bowl of internal radius IS cm contains a liquid. The liquid is to be filled into cylindrical-shaped bottles of diameter S cm and height 6 cm. How many bottles are necessary to empty the bowl? (C.B.S.E. 2001C)
Solution:
Internal radius of hemispherical bowl (r) = 15 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 18

Question 18.
In a cylindrical vessel of diameter 24 cm, filled up with sufficient quantity of water, a solid spherical ball of radius 6 cm is completely immersed. Find the increase in height of water level.
Solution:
Diameter of the cylindrical vessel = 24 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 19

Question 19.
 A hemisphere of lead of radius 7 cm is cast into a right circular cone of height 49 cm. Find the radius of the base.
Solution:
Radius of hemisphere of lead (r1) = 7 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 20

Question 20.
A solid metallic sphere of diameter 28 cm is melted and recast into a number of smaller cones, each of diameter 4\((\frac { 2 }{ 3 } )\)cm and height 3 cm. Find the number of cones so formed. (C.B.S.E. 2004)
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 21

Question 21.
The diameter of a copper sphere is 18 cm. The sphere is melted and is drawn into a long wire of uniform circular cross section. If the length of the wire is 108 m, find its diameter. (C.B.S.E. 1994)
Solution:
Diameter of copper sphere – 18 cm 18
Radius (R) = \((\frac { 18 }{ 2 } )\) = 9 cm 4
Volume = \((\frac { 4 }{ 3 } )\) π (R³)
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 22

Question 22.
A hemisphere of lead of radius 7 cm is cast into a right circular cone of height 49 cm. Find the radius of the base.
Solution:
Radius of hemisphere (R) = 7 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 23

Question 23.
A metallic sphere of radius 10.5 cm is melted and thus recast into small cones, each of radius 3.5 cm and height 3 cm. Find how many cones are obtained. (C.B.S.E. 2004)
Solution:
Radius of sphere (R) = 10.5 cm
∴ Volume of sphere =\((\frac { 4 }{ 3 } )\) πR³
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 24

Question 24.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. Show that their volumes are in the ratio 1:2:3.
Solution:
Let radius of a cone, a hemisphere and a cylinder be r
and height in each case = h
∴ h = r
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 25

Question 25.
A hollow sphere of internal and external diameters 4 and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone.
Solution:
Outer diameter of a hollow sphere = 8 cm
∴ Outer radius (R) = \((\frac { 8 }{ 2 } )\) = 4 cm
and inner diameter = 4 cm
∴ Inner radius (r)=\((\frac { 4 }{ 2 } )\) =2 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 26

Question 26.
The largest sphere is carved out of a cube of the side 10.5 cm. Find the volume of the sphere.
Solution:
Side of a cube = 10.5 cm
∵ The largest sphere is carved out of the cube,
∴ Diameter of the cube = side of the cube = 10.5 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 27

Question 27.
Find the weight of a hollow sphere of metal having internal and external diameters as 20 cm and 22 cm, respectively if 1 cm³ of metal weighs 21 g.
Solution:
Internal diameter of a hollow sphere = 20 cm
and external diameter = 22 cm
∴ Outer radius (R) = \((\frac { 22 }{ 2 } )\) = 11 cm 20
and inner radius = \((\frac { 20 }{ 2 } )\) = 10 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 28

Question 28.
A solid sphere of radius ‘r’ is melted and recast into a hollow cylinder of uniform thickness. If the external radius of the base of the cylinder is 4 cm, its height 24 cm and thinkness 2 cm, find the value of ‘r’.
Solution:
Radius of solid sphere = r
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 29

Question 29.
Lead spheres of diameter 6 cm are dropped into a cylindrical beaker containing some water and are fully submerged. If the diameter of the beaker is 18 cm and water rises by 40 cm find the number of lead spheres dropped in the water.
Solution:
Diameter of cylindrical diameter = 18 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 30

Question 30.
The height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm and height 4 cm arc cut off. Find the volume of the remaining solid.
Solution:
Diameter of right solid cylinder = 7 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 31

Question 31.
A solid is composed of a cylinder with hemispherical ends. If the length of the whole solid is 108 cm and the diameter of the cylinder is 36 cm, find the cost of polishing the surface at the rate of 7 paise per cm2. (Use TC = 3.1416)
Solution:
Total height of the solid =108 cm
Each diameter of base of hemispherical part = 36 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 32

Question 32.
The surface area of a sphere is the same as the curved surface area of a cone having the radius of the bases as 120 cm and height 160 cm. Find the radius of the sphere.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 34

Question 33.
 A right circular cylinder and a right circular cone have equal bases and equal heights. If their curved surfaces are in the ratio 8 : 5, determine the ratio of the radius of the base to the height of either of them.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 35

Question 34.
A rectangular vessel of dimensions 20 cm x 16 cm x 11 cm is full of water. This water is poured into a conical vessel. The top of the conical vessel has its radius 10 cm. If the conical vessel is filled completely, determine its height. (Use π = 22/7)
Solution:
Dimension of rectangular vessel are 20 cm x 16 cm x 11 cm
Volume of vessel = 20 x 16 x 11 cm³= 3520 cm³
∴ Volume of water in conical vessel = 3520 cm³
Radius of the top of vessel = 10 cm
Let h be its height, then
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 36

Question 35.
If r1 and r2 be the radii of two solid metallic spheres and if they are melted into one solid sphere, prove that the radius of the new sphere is (r1³ + r1³ )1/3.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 37

Question 36.
A solid metal sphere of 6 cm diameter is melted and a circular sheet of thickness 1 cm is prepared. Determine the diameter of the sheet.
Solution:
Diameter of solid sphere = 6 cm 6
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 38

Question 37.
A hemispherical tank full of water is \((\frac { 25 }{ 7 } )\) emptied by a pipe at the rate of  litres per second. How much time will it take to half-empty the tank, if the tank is 3 metres in diameter ?
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 39

Question 38.
Find the number of coins, 1.5 cm is diameter and 0.2 cm thick, to be melted to form a right circular cylinder of height 10 cm and diameter 4.5 cm.
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 40

Question 39.
The radius of the base of a right circular cone of semi-vertical angle a is r. Show that its volume is \((\frac { 1 }{ 3 } )\) πr³ cot a and curved surface area is πr² cosec α.
Solution:
Radius of circular cone = r
and semi vertical angle = α
Let AO = h and slant height AC = l
In ΔAOC, AO ⊥ BC
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 41

Question 40.
An iron pillar consists of a cylindrical portion 2.8 m high and 20 cm in diameter and a cone 42 cm high is surmounting it. Find the weight of the pillar, given that 1 cubic cm of iron weighs 7.5 gm.
Solution:
Diameter of cylindrical portion = 20 cm
∴ Radius (r) = \((\frac { 20 }{ 2 } )\)  = 10 cm
Height of (h1) = 2.8 m = 280 cm
and height of cone (h2) = 42 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 42

Question 41.
A circus tent is cylindrical to a height of 3 metres and conical above it. If its diameter is 105 m and the slant height of the conical portion is 53 m, calculate the length of the canvas 5 m wide to make the required tent.
Solution:
Diameter of the tent = 105 m
∴ Radius (r) = \((\frac { 105 }{ 2 } )\)  m
Height of cylindrical part (h1) = 3m
Slant height of conical part (h2) – 53 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 43
∴ Total surface area of the tent = curved surface area of the conical part + curved surface area of the cylindrical area
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 44

Question 42.
Height of a solid cylinder is 10 cm and diameter 8 cm. Two equal conical hole have been made from its both ends. If the diameter of the holes is 6 cm and height 4 cm, find (i) volume of the cylinder, (ii) volume of one conical hole, (iii) volume of the remaining solid.
Solution:
Height of the solid cylinder (h1) = 10 cm
Diameter = 8 cm
∴Radius (r1) = \((\frac { 8 }{ 2 } )\) = 4 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 45

Question 43.
The height of a solid cylinder is 15 cm and the diameter of its base is 7 cm. Two equal conical holes each of radius 3 cm, and height 4 cm are cut off. Find the volume of the remaining solid.
Solution:
Diameter of the base of a cylinder = 7 cm
∴ Radius (r1) = \((\frac { 7 }{ 2 } )\) cm
Height of cylinder (h1) = 15 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 46

Question 44.
A solid is composed of a cylinder with hemispherical ends. If the length of the whole solid is 108 cm and the diameter of the cylinder is 36 cm, find the cost of polishing the surface at the rate of 7 paise per cm2. (Useπ = 3.1416)
Solution:
Total height of the solid =108 cm
Diameter of base of each hemisphere = 36 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 47

Question 45.
The largest sphere is to be curved out of a right circular cylinder of radius 7 cm and height 14 cm. Find the volume of the sphere.
Solution:
Radius of cylinder (r) = 7 cm
and height (h) = 14 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 48
The diameter of the largest sphere curved out of the given cylinder = diameter of the cylinder
= 2 x 7 = 14 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 49

Question 46.
A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of the base of the cylinder or the cone is 24 m. The height of the cylinder is 11 m. If the vertex of the cone is 16 m above the ground, find the area of the canvas required for making the tent. (Use π = 22/7)
Solution:
Diameter of the base of the cone = 24 m
∴  Radius (r) = \((\frac { 24 }{ 2 } )\) = 12 m
Height of the cylindrical part (h1) = 11 m
Total height of the tent = 16 m
Height of the conical part (h2)
= 16- 11 = 5 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 50

Question 47.
Area of the canvas required for the tent = 1320 m2 47. A toy is in the form of a cone mounted on a hemisphere of radius 3.5 cm. The total height of the toy is 15.5 cm find the total surface area and volume of the toy. (C.B.S.E. 2000, 2002)
Solution:
Radius of the toy (r) = 3.5 cm
Total height of the toy = 15.5 cm
∴ Height of the conical part = 15.5 – 3.5 = 12 cm
Slant height of the conical part (l)
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 51
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 52

Question 48.
A cylindrical container is filled with ice-cream, whose diameter is 12 cm and height is 15 cm. The whole ice-cream is distributed to 10 children in equal cones having hemispherical tops. If the height of the conical portion is twice the diameter of its base, find the diameter of the ice-cream.
Solution:
Diameter of the cylindrical container = 12 cm
Radius (r1) = \((\frac { 12 }{ 2 } )\) = 6 cm
Height (h1) = 15 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 53
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 54

Question 49.
Find the volume of a solid in the form of a right circular cylinder with hemi-spherical ends whose total length is 2.7 m and the diameter of each hemispherical end is 0.7 m.
Solution:
Total length of solid = 2.7 m
Diameter of each hemisphere at the ends = 0.7 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 55
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 56

Question 50.
A tent of height 8.25 m is in the form of a right circular cylinder with diameter of base 30 m and height 5.5 m, surmounted by a right circular cone of the same base. Find the cost of the canvas of the tent at the rate of Rs. 45 per m².
Solution:
Total height of the tent = 8.25 m
Height of cylindrical part (h1) = 5.5 m
∴ Height of conical part (h2) = 8.25 – 5.5 = 2.75m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 57
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 58

Question 51.
An iron pole consisting of a cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that 1 cm³ of iron has 8 gram mass approximately. (Use π = 355/115)
Solution:
Diameter of the base of the cylindrical pole = 12 cm
∴ Radius (r) = \((\frac { 12 }{ 2 } )\) = 6 cm
Height of cylindrical portion (h1) = 110 cm
and height of conical portion (h2) = 9 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 59
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 60

Question 52.
The interior of a building is in the form of a cylinder of base radius 12 m and height 3.5 m, surmounted by a cone of equal base and slant height 12.5 m. Find the internal curved surface area and the capacity of the building.
Solution:
Radius of the building (r) = 12m
Height of the cylindrical portion (h1) = 3.5 m and
slant height of conical portion (l) = 12.5 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 61
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 62

Question 53.
A right angled triangle with sides 3 cm and 4 cm is revolved around its hypotenuse. Find the volume of the double cone thus generated.
Solution:
In right angled ΔABC, ∠B = 90°
AB = 3 cm and BC = 4 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 63
Now revolving the triangle along CA,
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 64
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 65

Question 54.
A toy is in the form of a cone mounted on a hemisphere with the same radius. The diameter of the base of the conical portion is 6 cm and its height is 4 cm. Determine the surface area of the toy (Use π = 3.14).
Solution:
Diameter of the base of the toy = 6 cm
∴ Radius (r) = \((\frac { 6 }{ 2 } )\) = 3 cm
Height of conical portion (h) = 4 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 66

Question 55.
Find the mass of a 3.5 m long lead pipe, if the external diameter of the pipe is 2.4 cm, thickness of the metal is 2 mm and the mass of 1 cm3 of lead is 11.4 grams.
Solution:
External diameter of a cylindrical pipe = 2.4 cm
Radius (R) = \((\frac { 2.4 }{ 2 } )\) = 1.2 cm
Thickness of the pipe = 2 mm =\((\frac { 2 }{ 10 } )\) = 0.2 cm
∴ Inner radius (r) = 1.2 – 0.2 = 1.0 cm
Height (length) of the pipe (h) = 3.5 m
= 350 cm
Volume of the mass of the pipe = πh (R² – r²)
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 67

Question 56.
A solid is in the form of a cylinder with hemispherical ends. Total height of the solid is 19 cm and the diameter of the cylinder is 7 cm. Find the volume and total surface area of the solid.
Solution:
Total height of the solid = 19 cm
Diameter of the cylinder = 7 cm
Radius (r) = \((\frac { 7 }{ 2 } )\) cm
Height of the cylinder = 19 – 2 x \((\frac { 7 }{ 2 } )\) cm
= 19-7 =12cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 68
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 69

Question 57.
A golf ball has diameter equal to 4.2 cm. Its surface has 200 dimples each of radius 2 mm. Calculate the total surface area which is exposed to the surroundings assuming that the dimples are hemi-spherical.
Solution:
Diameter of the golf ball = 4.2 cm
∴  Radius (R) = \((\frac { 4.2 }{ 2 } )\) =2.1 cm
Radius of each hemispherical dimples (r)  = 2 mm = \((\frac { 2 }{ 10 } )\) = \((\frac { 2 }{ 5 } )\) cm
Curved surface area of one dimple = 2πr²
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 70

Question 58.
The radii of the ends of a bucket of height 24 cm are 15 cm and 5 cm. Find its capacity. (Take π = 22/7).
Solution:
Height of the bucket (frustum) (h) = 24 cm
Upper radius (r1) = 15 cm
and lower radius (r2) = 5 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 71

Question 59.
The radii of the ends of a bucket 30 cm high are 21 cm and 7 cm. Find its capacity in litres and the amount of sheet required to make this bucket.
Solution:
Height of the bucket (frustum) (h) = 30 cm
Upper radius (r1) = 21 cm
and lower radius (r2) = 7 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 72
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 73

Question 60.
The radii of the ends of a frustum of a right circular cone are 5 metres and 8 metres and its lateral height is 5 metres. Find the lateral surface and volume of the frustum.
Solution:
Upper radius of a frustum (r1) = 8 m
and lower radius (r2) = 5 m
Lateral height (l) = 5m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 74

Question 61.
A frustum of a cone is 9 cm thick and the diameters of its circular ends are 28 cm and 4 cm. Find the volume and lateral surface area of the frustum. (Take π = 22/7)
Solution:
Upper diameter = 28 cm
and lower diameter = 4 cm
Height (h) = 9 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 75
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 76

Question 62.
A bucket is in the form of a frustum of a cone and holds 15.25 litres of water. The diameters of the top and bottom are 25 cm and 20 cm respectively. Find its height and area of tin used in its construction.
Solution:
Water in a bucket (frustum) = 15.25l
Upper diameter = 25 cm
and lower diameter = 20 cm
∴ Upper radius (r1) = \((\frac { 25 }{ 2 } )\) cm
and lower radius (r2) = \((\frac { 20 }{ 2 } )\) cm =10 cm
Volume = 15.25 /= 1525 x 10 cm³ = 15250 cm³
Let h be its height
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 77

Question 63.
If a cone of radius 10 cm is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base. Compare the volumes of the two parts. (C.B.S.E. 2000C)
Solution:
Radius of the cone (r1) = 10 cm
Cone is divided into 2 parts Such that PQ || AB
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 78
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 79

Question 64.
A tent is of the shape of a right circular cylinder upto a height of 3 metres and then becomes a right circular cone with a maximum height of 13.5 pnetres above the ground. Calculate the cost of painting the inner side of the tent at the rate of Rs. 2 per square metre, if the radius of the base is 14 metres
Solution:
Radius of the cylinder (r) = 14 m
and total height of the tent = 13.5 m
Height of the cylindrical part (h1) = 3 m
Height of conical part (h2) = 13.5-3.0 = 10.5m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 80

Question 65.
An oil funnel of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height be 22 cm, the diameter of the cylindrical portion 8 cm and the diameter of the top of the funnel 18 cm, find the area of the tin required. (Use : π = 22/7).
Solution:
Upper diameter of the frustum = 18 cm
and  lower diameter = 8m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 81
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 82

Question 66.
A solid cylinder of diameter 12 cm and height 15 cm is melted and recast into toys with the shape of a right circular cone mounted on a hemisphere of radius 3 cm. If the height of the toy is 12 cm, find the number of toys so formed. (C.B.S.E. 2006C)
Solution:
Diameter of solid cylinder = 12 cm
and height (h1) = 15 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 83
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 84

Question 67.
A container open at the top, is in the form of a frustum of a cone of height 24 cm with radii of its lower and upper circular ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container at the rate of ₹21 per litre. (Use π = 22/7)
Solution:
Upper radius (R) = 20 cm
Lower radius (r) = 8 cm
Height (h) = 24 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 85

Question 68.
 A cone of maximum size is carved out from a cube of edge 14 cm. Find the . surface area of the cone and of the remaining solid left out after the cone carved out. [NCERT Exemplar]
Solution:
The cone of maximum size that is carved out from a cube of edge 14 cm will be of base radius 7 cm and the height 14 cm.
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 86

Question 69.
A cone of radius 4 cm is divided into two parts by drawing a plane through the mid point of its axis and parallel to its base. Compare the volumes of two parts. [NCERT Exemplar]
Solution:
Let h be the height of the given cone. One dividing the cone through the mid-point of its axis and parallel to its base into two parts, we obtain the following figure:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 87

Question 70.
A wall 24 m, 0.4 m thick and 6 m high is constructed with the bricks each of dimensions 25 cm x 16 cm x 10 cm. If the mortar occupies \((\frac { 1 }{ 10 } )\) th of the volume of the wall, then find the number of bricks used in constructing the wall. [NCERT Exemplar]
Solution:
Given that, a wall is constructed with the help of bricks and mortar.
∴ Number of bricks
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 88
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 89

Question 71.
A bucket is in the form of a frustum of a cone and holds 28.490 litres of water. The radii of the top and bottom are 28 cm and 21 cm respectively. Find the height of the bucket. [NCERT Exemplar] 
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 90

Question 72.
Marbles of diameter 1.4 cm are dropped into a cylindrical beaker of diameter 7 cm containing some water. Find the number of marbles that should be dropped into the beaker so that the water level rises by 5.6 cm. [NCERT Exemplar]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 91

Question 73.
Two cones with same base radius 8 cm and height 15 cm are joined together along their bases. Find the surface area of the shape formed. [NCERT Exemplar]
Solution:
If two cones with same base and height are joined together along their bases, then the shape so formed is look like as figure shown.
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 92

Question 74.
From a solid cube of side 7 cm, a conical cavity of height 7 cm and radius 3 cm is hollowed out. Find the volume of the remaining solid. [NCERT Exemplar]
Solution:
Given that, side of a solid cube (a) = 1 cm
Height of conical cavity i.e., cone, h = 7 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 93
Since, the height of conical cavity and the side of cube is equal that means the conical cavity fit vertically in the cube.
Radius of conical cavity i. e., cone, r = 3 cm
⇒ Diameter = 2 x r = 2 x 3 = 6 cm
Since, the diameter is less than the side of a cube that means the base of a conical cavity is not fit inhorizontal face of cube.
Now, volume of cube = (side)³ = a³ = (7)³ = 34³ cm³
and volume of conical cavity i.e., cone
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 94

Question 75.
Two solid cones A and B are placed in a cylindrical tube as shown in the figure. The ratio of their capacitites are 2 : 1. Find the heights and capacities of the cones. Also, find the volume of the remaining portion of the cylinder. [NCERT Exemplar]
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 95
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 96
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 97

Question 76.
An icecream cone full of icecream having radius 5 cm and height 10 cm as shown’in the figure. Calculate the volume of icecream, provided that its 1/6 parts is left unfilled with icecream.
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 98
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise 99

 

Hope given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2

RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2

Other Exercises

Question 1.
Show that the sequence defined by an = 5n – 7 is an A.P., find its common difference.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2 1

Question 2.
Show that the sequence defined by an = 3n² – 5 is not an A.P.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2 2

Question 3.
The general term of a sequence is given by an = -4n + 15. Is the sequence an A.P.? If so, find its 15th term and the common difference.
Solution:
General term of a sequence
an = -4n + 15
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2 3

Question 4.
Write the sequence with nth term :
(i) an = 3 + 4n
(ii) an = 5 + 2n
(iii) an = 6 – n
(iv) an = 9 – 5n
Show that all of the above sequences form A.P.
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2 4
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2 5

Question 5.
The nth term of an A.P. is 6n + 2. Find the common difference. [CBSE 2008]
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2 6

Question 6.
Justify whether it is true to say that the sequence, having following nth term is an A.P.
(i) an = 2n – 1
(ii) an = 3n² + 5
(iii) an = 1 + n + n²
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2 7
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2 8
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2 9

Hope given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1

RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1

Other Exercises

Question 1.
Write the first five terms of each of the following sequences whose nth terms are:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 1
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 2
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 3
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 4
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 5
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 6

Question 2.
Find the indicated terms in each of the following sequences whose nth terms are:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 7
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 8

Question 3.
Find the next five terms of each of the following sequences given by :
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 9
Solution:
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 10
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 11
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 12
RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 13

Hope given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

CA Foundation Business Economics Study Material – Elasticity of Demand

CA Foundation Business Economics Study Material Chapter 2 Theory of Demand and Supply – Elasticity of Demand

Elasticity of Demand

  • Elasticity of demand is defined as the responsiveness or sensitiveness of the quantity demanded of a commodity to the changes in any one of the variables on which demand depends.
  • These variables are price of the commodity, prices of the related commodities, income of the consumers and many other factors on which demand depends.
  • Accordingly, we have price elasticity, cross elasticity, elasticity of substitution, income elasticity and advertisement elasticity.
  • Unless mentioned otherwise, it is price elasticity of demand which is generally referred.

Price Elasticity of Demand

  • Price elasticity measures the degree of responsiveness of quantity demanded of a commodity to a change in its price, given the consumer’s income, his tastes and prices of all other goods.
  • It reflects how sensitive buyers are to change in price.
  • Price elasticity of demand can be defined “as a ratio of the percentage change in the quantity demanded of a commodity to the percentage change in its own price”.
  • It may be expressed as follows:
    ca-foundation-business-economics-study-material-elasticity-of-demand-1
  • Rearranging the above expression we get:
    ca-foundation-business-economics-study-material-elasticity-of-demand-2
  • Since price and quantity demanded are inversely related, the value of price elasticity coefficient will always be negative. But for the value of elasticity coefficients we ignore the negative sign and consider the numerical value only. .

The value of elasticity coefficients will vary from zero to infinity.

  • When the coefficient is zero, demand is said to be perfectly inelastic.
  • When the coefficient lies between zero and unity, demand is said to be inelastic.
  • When coefficient is equal to unity, demand has unit elasticity.
  • When coefficient is greater than one, demand is said to elastic.
  • In extreme cases co-efficient could be infinite.

The degrees (types) of price elasticity of demand

Price elasticity measures the degree of responsiveness of quantity demanded of a commodity to a change in its price. Depending upon the degree of responsiveness of the quantity demanded to the price changes, we can have the following kinds of price elasticity of demand.

1. Perfectly Inelastic Demand: (Ep = 0):
ca-foundation-business-economics-study-material-elasticity-of-demand-3
When change in price has no effect on quantity demanded, then demand is perfectly inelastic. E.g. – If price falls by 20% and the quantity demanded remains unchanged then,
Ep = 0/20 = 0. In this case, the demand curve is a vertical straight line curve parallel to y-axis as shown in the figure.
The figure shows that, whatever the price, quantity demanded of the commodity remains unchanged at OQ.

2. Perfectly Elastic Demand: (Ep = ∞):
ca-foundation-business-economics-study-material-elasticity-of-demand-4
When with no change in price or with very little change in price, the demand for a commodity expands or contracts to any extent, the demand is said to be perfectly elastic. In this case, the demand curve is a horizontal and parallel to X-axis.
The figure shows that demand curve DD is parallel to X-axis which means that at given price, demand is ever increasing.

3. Unit Elastic Demand: (Ep = 1):
ca-foundation-business-economics-study-material-elasticity-of-demand-5
When the percentage or proportionate change in price is equal to the percentage or proportionate change in quantity demanded, then the demand is said to be unit elastic. E.g. If price falls by 10% and the demand rises by 10% then, Demand Curve DD is a rectangular hyperbola curve suggesting unitary elastic demand.
Ep = 10/10 = 1

4. Relatively Elastic Demand: ( Ep > 1):
ca-foundation-business-economics-study-material-elasticity-of-demand-6
When a small change in price leads to more than proportionate change in quantity demanded then the demand is said to be relatively elastic E.g. If price falls by 10% and demand rises by 30% then, Ep  = 30/10 = 3 > 1. The coefficient of price elasticity would be somewhere between ONE and INFINITY. The elastic demand curve is flatter as shown in figure.

Demand curve DD is flat suggesting that the demand is relatively elastic or highly elastic. Relatively elastic demand occurs in case of less urgent wants or if the expenditure on commodity is large or if close substitutes are available.

5. Relatively Inelastic Demand: (Ep < 1):
ca-foundation-business-economics-study-material-elasticity-of-demand-7
When a big change in price leads to less than proportionate change in quantity demanded, then the demand is said to be relatively inelastic. E.g. If price falls by 20% and demand rises by 5% then, Ep  = 5/20 = 5 < 1 The coefficient of price
elasticity is somewhere between ZERO and ONE. The demand curve in this case has steep slope.

Demand curve DD is steeper suggesting that demand is less elastic or relatively inelastic. Relatively inelastic demand occurs in case compulsory goods ie. necessities of life.

Measurement of price elasticity of demand

The different methods of measuring price elasticity of demand are:

  1. The Percentage or Ratio or Proportional Method,
  2. The Total Outlay Method,
  3. The Point or Geometrical Method, and
  4. The Arc Method.

1. The Percentage Method
This method is based on the definition of elasticity of demand. The coefficient of price elasticity of demand is measured by taking ratio of percentage change in demand to the percentage change in price. Thus, we measure the price elasticity by using the following formula
ca-foundation-business-economics-study-material-elasticity-of-demand-8

  • If the coefficient of above ratio is equal to ONE or UNITY, the demand will be unitary.
  • If the coefficient of above ratio is MORE THAN ONE, the demand is relatively elastic.
  • If the coefficient of above ratio is LESS THAN ONE, the demand is relatively inelastic.

2. The Total Outlay or Expenditure Method or Seller’s Total Revenue Method

The total outlay refers to the total expenditure done by a consumer on the purchase of a commodity. It is obtained by multiplying the price with the quantity demanded. Thus,
Total Outlay (TO) = Price (P) × Quantity (Q)
TO = P × Q
In this method, we measure price elasticity by examining the change in total outlay due to change in price.
Dr. Alfred Marshall laid the following propositions:

  • When with the change in price, the TO remains unchanged, Ep = 1.
  • When with a rise in price, the TO falls or with a fall in price, the TO rises, Ep > 1.
  • When with a rise in price, the TO also rises and with a fall in price, the TO also falls, Ep > 1

ca-foundation-business-economics-study-material-elasticity-of-demand-9

However, total outlay method of measuring price elasticity is less exact. This method only classifies elasticity into elastic, inelastic and unit elastic.
The exact and precise coefficient of elasticity cannot be found out with this method.

3. The Point Method or Geometric Method

  • The point elasticity method, we measure elasticity at a given point on a demand curve.
  • This method is useful when changes in price and quantity demanded are very small so that they can be considered one and the same point only.
  • E.g. If price of X commodity was Rs. 5,000 per unit and now it changes to Rs. 5002 per unit which is very small change. In such a situation we measure elasticity at a point on
    ca-foundation-business-economics-study-material-elasticity-of-demand-10
  • Diagrammatically also we can find elasticity at a point by using the formula—
    ca-foundation-business-economics-study-material-elasticity-of-demand-11

Figure:

  • The figure shows that even though the shape of the demand curve is constant, the elasticity is different at different points on the curve.
  • If the demand curve is not a straight line curve, then in order to measure elasticity at a point on demand curve we have to draw tangent at the given point and then measure elasticity using the above formula.
  • We can also find out numerical elasticities on different points.

4. The Arc Elasticity Method

  • When there is large change in the price or we have to measure elasticity over an arc of the demand curve, we use the “arc method” to measure price elasticity of demand.
  • The arc elasticity is a measure of the “average elasticity” ie. elasticity at MID-POINT that connects the two points on the demand curve.
  • Thus, an arc is a portion of a curved line, hence a portion of a demand curve. Here instead of using original or new data as the basis of measurement, we use average of the two.
    ca-foundation-business-economics-study-material-elasticity-of-demand-12
  • The formula used is
    ca-foundation-business-economics-study-material-elasticity-of-demand-13

Determinants of price elasticity of demand

Price elasticity of demand which measures the degree of responsiveness of quantity demanded of a commodity to a change in price (other things remaining unchanged) depends on the following factors:—

1. Nature of commodity:

  • The demand for necessities of life like food, clothing, housing etc. is less elastic or inelastic because people have to buy them whatever be the price.
  • Whereas, demand for luxury goods like cars, air-conditioners, cellular phone, etc. is elastic.

2. Availability of Substitutes:

  • If for a commodity wide range of close substitutes are available ie. if a commodity is easily replaceable by others, its demand is relatively elastic. E.g. Demand for cold drinks like Thumbs-up, Coca-cola, Limca, etc.
  • Conversely, a commodity having no close substitute has inelastic demand. E.g. Salt (but demand for TATA BRAND SALT is elastic.)

3. Number of uses of a commodity:

  • A commodity which has many uses will have relatively elastic demand.
    E.g. Electricity can be put to many uses like lighting, cooking, motive-power, etc. If the price of electricity falls, its consumption for various purposes will rise and vice versa.
  • On the other hand if a commodity has limited uses will have inelastic demand.

4. Price range:

  • If price of a commodity is either too high or too low, its demand is inelastic but those which are in middle price range have elastic demand.

5. Position of a commodity in the budget of consumer:

  • If a consumer spends a small proportion of his income to purchase a commodity, the demand is inelastic. E.g. Newspaper, match box, salt, buttons, needles.
  • But if consumer spends a large proportion of his income to purchase a commodity, the demand is elastic E.g. Clothes, milk, etc.

6. Time period:

  • The longer any price change remains the greater is the price elasticity of demand.
    On the other hand, shorter any price change remains, the lesser is the price elasticity of demand. .

7. Habits:

  • Habits makes the demand for a commodity relatively inelastic. E.g. A smoker’s demand for cigarettes tend to be relatively inelastic even at higher price.

8. Tied Demand (Joint Demand):

  • Some goods are demanded because they are used jointly with other goods. Such goods normally have inelastic demand as against goods having autonomous demand.
    E.g. Printers & Cartridges.

Knowledge of the concept of elasticity of demand and the factors that may change it is of great IMPORTANCE in practical life. The concept of elasticity of demand is helpful to-

  1. Business Managers as it helps then to recognise the effect of price change on their total sales and revenues. The objective of a firm is profit maximization. If demand is ELASTIC for the product, the managers can fix a lower price in order to expand the volume of sales and vice versa.
  2. Government for determining the prices of goods and services provided by them. E.g.- transport, electricity, water, cooking gas, etc. It also helps governments to understand the nature of response of demand when taxes are raised and its effect on the tax revenues. E.g.- Higher taxes are imposed on the goods having INELASTIC DEMAND like cigarettes, liquor, etc.

Income Elasticity of Demand

  • The income elasticity of demand measures the degree of responsiveness of quantity demanded to changes in income of the consumers.
  • The income elasticity is defined as a ratio of percentage change in the quantity demanded to the percentage change in income.
    ca-foundation-business-economics-study-material-elasticity-of-demand-14
    ca-foundation-business-economics-study-material-elasticity-of-demand-15

The income elasticity of demand is POSITIVE for all normal or luxury goods and the income elasticity of demand is NEGATIVE for inferior goods. Income elasticity can be classified under five heads:-

ca-foundation-business-economics-study-material-elasticity-of-demand-16

  1. Zero Income Elasticity:
    • It means that a given increase in income does not at all lead to any increase in quantity demanded of the commodity.
    • In other words, demand for the commodity is completely income inelastic or Ey = 0
    • Commodities having zero income elasticity are called NEUTRAL GOODS.
    • E.g. – Demand in case of SALT, MATCH BOX, KEROSENE OIL, POST CARDS, etc.
  2. Negative Income Elasticity:
    • It means that an increase in income results in fall in the quantity demanded of the commodity or Ey < 0.
    • Commodities having negative income elasticity are called INFERIOR GOODS.
    • E.g. – Jawar, Bajra, etc.
  3. Unitary Income Elasticity:
    • It means that the proportion of consumer’s income spent on the commodity remains unchanged before and after the increase in income or Ey = 1. This represents a useful dividing line.
  4. Income Elasticity Greater Than Unity:
    • It refers to a situation where the consumers spends GREATER proportion of his income on a commodity when he becomes richer. Ey > 1,
    • E.g. In the case of LUXURIES like cars, T.V. sets, music system, etc.
  5. Income Elasticity Less Than Unity:
    • It refers to a situation where the consumer spends a SMALLER proportion of his income on a commodity when he becomes richer. Ey < 1,
    • E.g. In the case of NECESSITIES like rice, wheat, etc.

Cross elasticity of demand

  • Many times demand for two goods are related to each other.
  • Therefore, when the price of a particular commodity changes, the demand for other commodities changes, even though their own prices have not changed.
  • We measures this change under cross elasticity.

The cross elasticity of demand can be defined “as the degree of responsiveness of demand for a commodity to a given change in the price of some RELATED commodity” OR “as the ratio of percentage change in quantity demanded of commodity X to a given percentage change in the price of the related commodity Y”. Symbolically:
ca-foundation-business-economics-study-material-elasticity-of-demand-17

Cross elasticity of demand can be used to classify goods as follows:-

  1. Substitute Goods: E.g.: Tea and Coffee. The cross elasticity between two substitutes is always POSITIVE. If cross elasticity is infinite, the two goods are perfect substitute and if it is greater than zero but less than infinity, the goods are substitutes.
    ca-foundation-business-economics-study-material-elasticity-of-demand-18
  2. Independent Goods: E.g.: Pastry and Scooter. The two commodities are not related. The cross elasticity in such cases is ZERO.
  3. Complementary Goods: E.g.: Petrol and Car. If the price of petrol rise, its demand falls and along with it demand for cars also falls. The cross elasticity in such cases is NEGATIVE
    ca-foundation-business-economics-study-material-elasticity-of-demand-19

Advertisement or Promotional Elasticity of Demand

  • Demand of many goods is also influenced by advertisement or promotional efforts.
  • It means that the demand for a good is responsive to the advertisement expenditure incurred by a firm.
  • The measurement of the degree of responsiveness of demand of a good to a given change in advertisement expenditure is called advertisement or promotional elasticity of demand.
  • It measures the percentage change in demand to a give ONE PERCENTAGE change in advertising expenditure. It helps a firm to know the effectiveness of its advertisement campaign.
  • Advertisement elasticity of demand is POSITIVE. Higher the value, higher is change in demand to change in advertisement expenditure.
    ca-foundation-business-economics-study-material-elasticity-of-demand-20

The value of advertisement elasticity varies between zero and infinity. If-

  • Ea = 0, no change in demand to increase in advertisement expenditure
  • Ea > 0 but < 1, less than proportionate change in demand to a change in advertisement expenditure
  • Ea = 1, change in demand is equal to change in advertisement expenditure
  • Ea > 1, higher rate of change in demand than change in advertisement expenditure

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3

Other Exercises

Question 1.
A bucket has top and bottom diameters of 40 cm and 20 cm respectively. Find the volume of the bucket if its depth is 12 cm. Also, find the cost of tin sheet used for making the bucket at the rate of ?1.20 per dm2. (Use % = 3.14)
Solution:
Upper diameter = 40 cm
and lower diameter = 20 cm
∴  Upper radius (r1) = \((\frac { 40 }{ 2 } )\) = 20 cm
and lower radius (r2) = \((\frac { 20 }{ 2 } )\) = 10 cm
Depth or height (h) = 12 cm
Volume of the bucket
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 1

Question 2.
A frustum of a right circular cone has a diameter of base 20 cm, of top 12 cm, and height 3 cm. Find the area of its whole surface and volume.
Solution:
Base diameter of frustum = 20 cm 20
∴  Radius (r1) = \((\frac { 20 }{ 2 } )\) = 10 cm
and diameter of top = 12 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 2

Question 3.
The slant height of the frustum of a cone is 4 cm and the perimeters of its circular ends are 18 cm and 6 cm. Find the curved surface of the frustum.
Solution:
Perimeter of the top of frustum = 18 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 3

Question 4.
The perimeters of the ends of a frustum of a right circular cone are 44 cm and 33 cm. If the height of the frustum be 16 cm, find its volume, the slant surface and the total surface.
Solution:
Perimeter of the top of frustum = 44 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 4
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 5
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 6

Question 5.
If the radii of the circular ends of a conical bucket which is 45 cm high be 28 cm and 7 cm, find the capacity of the bucket. (Use π = 22/7). (C.B.S.E. 2000)
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 7

Question 6.
The height of a cone is 20 cm. A small cone is cut off from the top by a plane parallel to the base. If its volume be \((\frac { 1 }{ 125 } )\)  of the volume of the original cone, determine at what height above the base the section is made.
Solution:
Total height of the cone (h1) = 20 cm
Let a cone whose height is h2 is cut off Then height of the remaining portion (frustum)
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 8
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 9

Question 7.
If the radii of the circular ends of a bucket 24 cm high are 5 cm and 15 cm respectively, find the surface area of the bucket.
Solution:
Height of the bucket (frustum) (A) = 24 cm
Radius of the top (r1) = 15 cm 1
and radius of the bottom (r2) = 5 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 10

Question 8.
The radii of the circular bases of a frustum of a right circular cone are 12 cm and 3 cm and the height is 12 cm. Find the total surface area and the volume of the frustum.
Solution:
Height of the frustum (A) = 12 cm
Radius of the top (r1) = 12 cm
and radius of the bottom (r2) = 3 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 11

Question 9.
A tent consists of a frustum of a cone capped by a cone. If the radii of the ends of the frustum be 13 m and 7 m, the height of the frutum be 8 m and the slant height of the conical cap be 12 m, find the canvas required for the tent. (Take : π = 22/7)
Solution:
Radius of the bottom of the tent (r1) = 13 m
and radius of the top (r2) = 7 m
Height of frustum portion (h1) = 8 m
Slant height of the conical cap (l2) = 12 m
Let l1 be the slant height of the frustum portion, then
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 12

Question 10.
A milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively. Find the cost of milk at the rate of ₹44 per litre which the container can hold. [NCERT Exemplar]
Solution:
Given that, height of milk container (h) = 16 cm
Radius of lower end of milk container (r) = 8 cm
and radius of upper end of milk container (R) = 20 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 13
∴ Volume of the milk container made of metal sheet in the form of a frustum of a cone
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 14

Question 11.
A bucket is in the form of a frustum of a cone of height 30 cm with radii of its lower and upper ends as 10 cm and 20 cm respectively. Find the capacity and surface area of the bucket. Also, find the cost of milk which can completely fill the container, at the rate of ₹25 per litre. (Use π = 3.14) [NCERT Exemplar]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 15

Question 12.
A bucket is in the form of a frustum of a cone with a capacity of 12308.8 cm³ of water. The radii of the top and bottom circular ends are 20 cm and 12 cm respectively. Find the height of the bucket and the area of the metal sheet used in its making. (Use π = 3.14). [CBSE 2006C]
Solution:
Volume of frustum (bucket) = 12308.8 cm³
Upper radius (r1) = 20 cm
and lower radius (r2) = 12 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 16
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 17

Question 13.
A bucket made of aluminium sheet is of height 20 cm and its upper and lower ends are of radius 25 cm and 10 cm respectively. Find the cost of making the bucket if the aluminium sheet costs Rs. 70 per 100 cm². (Use π = 3.14) (C.B.S.E. 2006C)
Solution:
Height of bucket (frustum) (h) = 20 cm
Upper radius (r1) = 25 cm
and lower radius (r2) = 10
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 18

Question 14.
The radii of the circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Find its total surface area. (C.B.S.E. 2005)
Solution:
Upper radius of frustum (r1) = 3.3 cm
and lower radius (r2) = 27 cm
Slant height (l) = 10 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 19

Question 15.
A bucket made up of a metal sheet is in the form of a frustum of a cone of height 16 cm with diameters of its lower and upper ends as 16 cm and 40 cm respectively. Find the volume of the bucket. Also, find the cost of the bucket if the cost of metal sheet used is Rs. 20 per 100 cm². (Use π = 3.14) (CBSE 2008)
Solution:
Lower radius of bucket (r) = \((\frac { 16 }{ 2 } )\) = 8 cm
and upper radius (R) = \((\frac { 40 }{ 2 } )\) = 20 cm
Height (h) = 16
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 20

Question 16.
A solid is in the shape of a frustum of a cone. The diameter of the two circular ends are 60 cm and 36 cm and the leight is 9 ³cm. Find the area of its whole surface and the volume. [CBSE 2010]
Solution:
In a solid frustum upper diameter = 60 cm
∴ Radius (r1) = \((\frac { 60 }{ 2 } )\) = 30 cm
Lower diameter = 36 cm 36
∴ Radius (r2) = \((\frac { 36 }{ 2 } )\) = 18 cm
Height (h) = 9 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 21

Question 17.
A milk container is made of metal sheet in the shape of frustum of a cone whose volucrn is 10459\((\frac { 3 }{ 7 } )\) cm³. The radii of its lower and upper circular ends are 8 cm and 20 cm respectively. Find the cost of metal sheet used in making the container at the rate of Rs. 1.40 per cm². (Use π = 22.7) [CBSE 2010]
Solution:
Volume of frustum = 10459\((\frac { 3 }{ 7 } )\) cm3 73216
= \((\frac { 73216 }{ 7 } )\) cm³
Lower radius (r2) = 8 cm
and upper radius (r1) = 20 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 22
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 23

Question 18.
A solid cone of base radius 10 cm is cut into two parts through the mid-pint of its height, by a plane parallel to its base. Find the ratio in the volumes of two parts of the cone. [CBSE 2013]
Solution:
Radius of solid cone (r) = 10 cm
Let total height = h
In ΔAOB,
C is mid point of AO and CD || OB
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 24

Question 19.
A bucket open at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is 24 cm and the diameters of its upper and lower circular ends are 30 cm and 10 cm respectively. Find the cost of metal sheet used in it at the rate of ₹10 per 100 cm². (Use π = 3.14). [CBSE 2013]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 25

Question 20.
In the given figure, from the top of a solid cone of height 12 cm and base radius 6 cm, a cone of height 4 cm is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use π = 22/7 and \(\sqrt { 5 } \) = 2.236).  [ CBSE 2015]
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 26
Solution:
Total height of cone = 12 cm
Radius of its base = 6 cm
A cone of height 4 cm is cut out
Height of the so formed frustum = 12 – 4 = 8 cm
Let r be the radius of the cone cut out
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 27

Question 21.
The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
Solution:
Let the height and radius of the given cone be H and R respectively.
The cone is divided into two parts by drawing a plane through the mid point of its axis and parallel to the base.
Upper part is a smaller cone and the bottom part is the frustum of the cone.
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 28
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 29

Question 22.
A bucket, made of metal sheet, is in the form of a cone whose height is 35 cm and radii of circular ends are 30 cm and 12 cm. How many litres of milk it contains if it is full to the brim? If the milk is sold at ₹40 per litre, find the amount received by the person. [CBSE 2017]
Solution:
Radii of the bucket in the form of frustum of cone = 30 cm
and 12 cm Depth of the bucket = 35 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 30

Question 23.
A reservoir in the form of the frustum of a right circular cone contains 44 x 107 litres of water which fills it completely. The radii of the bottom and top of the reservoir are 50 metres and 100 metres respectively. Find the depth of water and the lateral surface area of the reservoir. (Take : π = 22/7)
Solution:
A reservoir is a frustum in shape and its upper radius (r1) = 100 m
Lower radius (r2) = 50 m
and capacity of water in it = 44 x 107 litres
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 31
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 32

P.Q. A metallic right circular cone 20 cm high and whose vertical angle is 90° is cut into two parts at the middle point of its axis by a plane parallel to the base. If the frustum so obtained be drawn into a wire  \((\frac { 1 }{ 16 } )\)cm, find the length of the wire.

Solution: In the cone ABC, ∠A = 90°, AL ⊥ BC and = 20 cm
It is cut into two parts at the middle point M on the axis AL
AL bisects ∠A also
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 33
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 34

Hope given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

CA Foundation Business Economics Study Material – Law of Demand

CA Foundation Business Economics Study Material Chapter 2 Theory of Demand and Supply – Law of Demand

The Law of Demand

  • The Law of Demand expresses the nature of functional relationship between the price of a commodity and its quantity demanded.
  • It simply states that demand varies inversely to the changes in price i.e. demand for a commodity expands when price falls and contracts when price rises.
  • “Law of Demand states that people will buy more at lower prices and buy less at higher prices, other things remaining the same.” (Prof. Samuelson)
  • It is assumed that other determinants of demand are constant and ONLY PRICE IS THE VARIABLE AND INFLUENCING FACTOR.
  • Thus, the law of demand is based on the following main assumptions:—
    1. Consumers income remain unchanged.
    2. Tastes and preferences of consumers remain unchanged.
    3. Price of substitute goods and complement goods remain unchanged.
    4. There are no expectations of future changes in the price of the commodity.
    5. There is no change in the fashion of the commodity etc.
  • The law can be explained with the help of a demand schedule and a corresponding demand curve.
  • Demand schedule is a table or a chart which shows the different quantities of commodity demanded at different prices in a given period of time.
  • Demand schedule can be Individual Demand Schedule or Market Demand Schedule.

Individual Demand Schedule is a table showing different quantities of commodity that ONE PARTICULAR CONSUMER is willing to buy at different level of prices, during a given period of time.

ca-foundation-business-economics-study-material-law-of-demand

Market Demand Schedule is a table showing different quantities of a commodity that ALL THE CONSUMERS are willing to buy at different prices, during a given period of time.

ca-foundation-business-economics-study-material-law-of-demand-1
(Assumption: There are only 2 buyers in the market)

Both individual and market schedules denotes an INVERSE functional relationship between price and quantity demanded. In other words, when price rises demand tends to fall and vice versa.

A demand curve is a graphical representation of a demand schedule or demand function.

  • A demand curve for any commodity can be drawn by plotting each combination of price and demand on a graph.
  • Price (independent variable) is taken on the Y-axis and quantity demanded (dependent variable) on the X-axis.

ca-foundation-business-economics-study-material-law-of-demand-2

  • Individual Demand Curve as well as Market Demand Curve slope downward from left to right indicating an inverse relationship between own price of the commodity and its quantity demanded.
  • Market Demand Curve is flatter than individual Demand Curve.

Reasons for the law of demand and downward slope of a demand curve are as follows:—

1. The Law of Diminishing Marginal Utility:

  • According to this law, other things being equal as we consume a commodity, the marginal utility derived from its successive units go on falling.
  • Hence, the consumer purchases more units only at a lower price.
  • A consumer goes on purchasing a commodity till the marginal utility of the commodity is greater than its market price and stops when MU = Price ie. when consumer is at equilibrium.
  • When the price of the commodity falls, MU of the commodity becomes greater than price and so consumer start purchasing more till again MU = Price.
  • It therefore, follows that the diminishing marginal utility implies downward sloping demand curve and the law of demand operates.

2. Change in the number of consumers:

  • Many consumers who were unable to buy a commodity at higher price also start buying when the price of the commodity falls.
  • Old customers starts buying more when price falls.

3. Various uses of a commodity:

  • Commodity may have many uses. The number of uses to which the commodity can be put will increase at a lower price and vice versa.

4. Income effect:

  • When price of a commodity falls, the purchasing power (ie. the real income) of the consumer increases.
  • Thus he can purchase the same quantity with lesser money or he can get more quantity for the same money.
  • This is called income effect of the change in price of the commodity.

5. Substitution effect:

  • When price of a commodity falls it becomes relatively cheaper than other commodities.
  • As a result the consumer would like to substitute it for other commodities which have now become more expensive.
    E.g. With the fall in price of tea, coffee’s price remaining the same, tea will be substituted for coffee.
  • This is called substitution effect of the change in price of the commodity.
  • Thus, PRICE EFFECT = INCOME EFFECT + SUBSTITUTION EFFECT as explained by Hicks and Allen.

Exceptions to the Law of Demand

  • Law of Demand expresses the inverse relationship between price and quantity demanded of a commodity. It is generally valid in most of the situations.
  • But, there are some situations under which there may be direct relationship between price and quantity demanded of a commodity.

These are known as exceptions to the law of demand and are as follows:—

1. Giffen Goods:

  • In some cases, demand for a commodity falls when its price fall and vice versa.
  • In case of inferior goods like jawar, bajra, cheap bread, etc. also called “Giffen Goods” (known after its discoverer Sir Robert Giffens) demand is of this nature.
  • When the price of such inferior goods fall, less quantity is purchased due consumer’s increased preference for superior commodity with the rise in their “real income” (Le. purchasing power).
  • Hence, other things being equal, if price of a Giffen good fall its demand also falls.
  • There is positive price effect in this case.

2. Conspicuous goods:

  • Some consumers measure utility of a commodity by its price i.e. if the commodity is expensive they think it has got more utility and vice versa.
  • Therefore, they buy less at lower price and more of it at higher price.
    E.g. Diamonds, fancy cars, dinning at 5 stars, high priced shoes, ties, etc….
  • Higher prices are indicators of higher utilities.
  • A higher price means higher prestige value and higher appeal and vice versa.
  • Thus a fall in their price would lead to fall in their quantities demanded. This is against the law of demand.
  • This was found out by Veblen in his doctrine of “Conspicuous Consumption” and hence this effect is called Vebleri effect or prestige effect.

3. Conspicuous necessities:

  • The demand for some goods is guided by the demonstration effect of the consumption pattern of a social group to which the person belongs.
    E.g. Television sets, refrigerators, music systems, cars, fancy clothes, washing machines etc.
  • Such goods are used just to demonstrate that the person is not inferior to others in group.
  • Hence, inspite of the fact that prices have been continuously rising, their demand does not show tendency to fall.

4. Future changes in prices:

  • When the prices are rising, households tend to purchase larger quantities of the commodity, out of fear that prices may go up further and vice versa.
    E.g. – Shares of a good company, etc.

5. Irrational behaviour of the consumers:

  • At times consumers make IMPULSIVE PURCHASES without any calculation about price and usefulness of the product. In such cases the law of demand fails.

6. Ignorance effect:

  • Many times households may demand larger quantity of a commodity even at a higher price because of ignorance about the ruling price of the commodity in the market.

7. Consumer’s illusion:

  • Many consumers have a wrong illusion that the quality of the commodity also changes with the price change.
  • A consumer may contract his demand with a fall in price and vice versa.

8. Demand for necessaries:

  • The law of demand does not hold true in case of commodities which are necessities of life. Whatever may be the price changes, people have to consume the minimum quantities of necessary commodities. E.g.- rice, wheat, clothes, medicines, etc.

DEMAND CURVE FOR ABOVE EXCEPTIONS IS POSITIVELY SLOPED

Expansion and Contraction of Demand

(changes in quantity demanded. Or movement along a demand curve)

  • The law of demand, the demand schedule and the demand curve all show that
    – when the price of a commodity falls its quantity demanded rises or expansion takes place and
    – when the price of a commodity rises its quantity demanded fall or contraction takes place.
  • Thus, expansion and contraction of demand means changes in quantity demanded due to change in the price of the commodity other determinants like income, tastes, etc. remaining constant or unchanged.
  • When price of a commodity falls, its quantity demanded rises. This is called expansion of demand.
  • When price of a commodity rises, its quantity demanded falls. This is called contraction of demand.
  • As other determinants of price like income, tastes, price of related goods etc. are constant, the position of the demand curve remains the same. The consumer will move upwards or downwards on the same demand curve.

ca-foundation-business-economics-study-material-law-of-demand-3
Figure : Expansion and Contraction of Demand

In the figure

  • At price OP quantity demanded is OQ.
  • With a fall in price to OP1, the quantity demanded rises from OQ toOQ1,. The coordinate point moves down from E to E1This is called ‘expansion of demand’ or ‘a rise in quantity demanded’ or ‘downward movement on the same demand curve’.
  • At price OP quantity demanded is OQ.
  • With a rise in price to P2, the quantity demanded falls from OQ to OQ2. The coordinate point moves up from E to E2. This is called ‘contraction of demand’ or ‘a fall in quantity demanded’ or ‘upward movement on the same demand curve’.
  • Thus, the downward movement on demand curve is known as expansion in demand and an upward movement on demand curve is known as contraction of demand.

Increase and Decrease in demand (changes in demand OR shift in demand curve)

  • When there is change in demand due to change in factors other than price of the commodity, it is called increase or decrease in demand.
  • It is the result of change in consumer’s income, tastes and preferences, changes in population, changes in the distribution of income, etc.
  • Thus, price remaining the same when demand rises due to change in factors other than price, it is called increase in demand. Here, more quantity is purchased at same price or same quantity is purchased at higher price.
  • Likewise price remaining the same when demand falls due to change in factors other than price, it is called decrease in demand. Here, less quantity is purchased at same price or same quantity is purchased at lower price.
  • In above cases demand curve shifts from its original position to rightward when demand increases and to leftward when demand decreases. Thus, change in demand curve as a result of increase or decrease in demand, is technically called shift in demand curve.

ca-foundation-business-economics-study-material-law-of-demand-4
Figure : Increase and Decrease in Demand

In the figure

  • Original demand curve is DD. At OP price OQ quantity is being demanded.
  • As the demand changes, the demand curve shifts either to the right (D1D1) or to the left (D2D2)
  • At D1D1, OQ1, quantity is being demanded at the price OP. This shows increase in demand (rightward shifts in demand curve) due to factor other than price.
  • At D2D2, QO2 quantity is being demanded at the price OP. This shows decrease in demand (leftward shift in demand curve) due to a factor other than price.
  • When demand of a commodity INCREASES due to factors other than price, firms can sell a larger quantity at the prevailing price and earn higher revenue.
  • The aim of a advertisement and sales promotion activities is to shift the demand curve to the right and to reduce the elasticity of demand.

 

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2

Other Exercises

Question 1.
A tent is in the form of a right circular cylinder surmounted by a cone. The diameter of cylinder is 24 m. The height of the cylindrical portion is 11 m while the vertex of the cone is 16 m above the ground. Find the area of canvas required for the tent.
Solution:
Diameter of the base of the tent = 24 m
∴ Radius (r)= \((\frac { 24 }{ 2 } )\)  = 12m
Total height of the tent = 16 m
Height of the cylindrical portion (h1) = 11 m
Height of the conical portion (h2) =16-11 = 5 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 1

Question 2.
A rocket is in the form of a circular cylinder closed at the lower end with a cone of the same radius attached to the top. The cylinder is of radius 2.5 m and height 21 m and the cone has the slant height 8 m. Calculate the total surface area and the volume of the rocket.
Solution:
Radius of the base of the rocket (r) = 2.5 m
Height of cylindrical portion (h1) = 21 m
Slant height of the conical portion (l) = 8 m
Let height of conical portion = h2
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 2
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 3

Question 3.
A tent of height 77 dm is in the form of a right circular cylinder of diameter 36 m and height 44
dm surmounted by a right circular cone. Find the cost of the canvas at Rs. 3.50 per m2 . (Use π = 22/7).
Solution:
Total height of the tent = 77 dm
Height of cylindrical part (h1) = 44 dm
= 4.4 m
Height of conical part (h2) = 7.7 – 4.4 = 3.3 m
Diameter of the base of the tent = 36 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 4
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 5

Question 4.
A toy is in the form of a cone surmounted on a hemisphere. The diameter of the base and the height of the cone are 6 cm and 4 cm, respectively. Determine the surface area of the toy. (Use π = 3.14).
Solution:
Diameter of the base of the toy = 6 cm
∴ Radius (r) = \((\frac { 6 }{ 2 } )\)  = 3 cm
Height (h) = 4 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 6
Total surface area of the toy = curved surface area of the conical part + surface area of the hemispherical part
= πrl + 2πr² = πr (l + 2r)
= 3.14 x 3 (5 + 6) = 3.14 x 3 x 11 cm²
= 3.14 x 33 = 103.62 cm²

Question 5.
A solid is in the form of a right circular cylinder, with a hemisphere at one end and a cone at the other end. The radius of the common base is 3.5 cm and the ~ heights of the cylindrical and conical portions are 10 cm and 6 cm, respectively. Find the total surface area of the solid. (Use π = 22/7)
Solution:
Radius of the common base (r) = 3.5 m
Height of cylindrical part (h1) = 10 cm
Height of conical part (h2) = 6 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 7
Now total surface area of the solid = curved surface of conical part + curved surface of cylindrical part + curved surface of hemispherical part
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 8

Question 6.
A toy is in the shape of a right circular cylinder with a hemisphere on one end and a cone on the other. The radius and height of the cylindrical part are 5 cm and 13 cm respectively. The radii of the hemispherical and conical parts are the same as that of the cylindrical part. Find the surface area of the toy if the total height of the toy is 30 cm. (C.B.S.E. 2002)
Solution:
Radius of the base of the cylindrical part (r) = 5 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 9
Height of cylindrical part (h1) = 13 cm
Height of the conical part (h2) = 30 – (13 + 5) = 30- 18 = 12 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 10

Question 7.
A cylindrical tub of radius 5 cm and length 9.8 cm is full of water. A solid in the form of a right circular cone mounted on a hemisphere is immersed in the tub. If the radius of the hemisphere is immersed in the tub. If the radius of the hemi-sphere is 3.5 cm and height of the cone outside the hemisphere is 5 cm, find the volume of the water left in the tub. (Take π = 22/7) (C.B.S.E. 2000C)
Solution:
Radius of the cylindrical tub (R) = 5 cm
and height (h1) = 9.8 cm
Radius of the solid (r) = 3.5 cm
and height of cone (h1) = 5 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 11
= 38.5 x 4 = 154 cm3
∴ Water flowed out of the tub = 154 cm³
Remaining water in the tub = 770 – 154
= 616 cm³

Question 8.
A circus tent has cylindrical shape surmounted by a conical roof. The radius of the cylindrical base is 20 m. The heights of the cylindrical and conical portions are 4.2 m and 2.1 m respectively. Find the volume of the tent.
Solution:
Radius of the tent (r) = 20 m
Height of the conical part (h1) = 2.1 m
and height of the cylindrical part (h2) = 4.2 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 12

Question 9.
A petrol tank is a cylinder of base diameter 21 cm and length 18 cm fitted with conical ends each of axis length 9 cm. Determine the capacity of the tank.
Solution:
Diameter of cylindrical part = 21 cm 21
∴ Radius (r) = \((\frac { 21 }{ 2 } )\) cm
Height of cylindrical part (h1) = 18 cm
and height of each conical part (h2) = 9 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 13

Question 10.
A conical hole is drilled in a circular cylinder of height 12 cm and base radius 5 cm. The height and the base radius of the cone are also the same. Find the whole surface and volume of the remaining cylinder.
Solution:
Base radius of the cylinder (r) = 5 cm
and height (h) = 12 cm
∴ Volume = πr2h = n (5)2 x 12 cm3 = 300π cm3
∵ The base and height of the cone drilled are the same as those of the cylinder
∴ Volume of cone = \((\frac { 1 }{ 3 } )\)πr2h
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 14

Question 11.
A tent is in the form of a cylinder of diameter 20 m and height 2.5 m, surmounted by a cone of equal base and height 7.5 m. Find the capacity of the tent and the cost of the canvas at Rs. 100 per square metre.
Solution:
Diameter of the base of the tent = 20 m
∴ Radius (r) =\((\frac { 20 }{ 2 } )\) = 10 m
Height of cylindrical part (h1) = 2.5 m
and height of conical part (h2) = 7.5 m
Slant height of the conical part (l)
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 15
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 16

Question 12.
A boiler is in the form of a cylinder 2 m long with hemispherical ends each of 2 metre diameter. Find the volume of the boiler.
Solution:
Diameter of the cylinder = 2 m
∴ Radius (r) = \((\frac { 1 }{ 3 } )\) = 1 m
Height (length) of cylindrical part (h) = 2 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 17

Question 13.
A vessel is a hollow cylinder fitted with a hemispherical bottom of the same base. The depth of the cylinder is \((\frac { 14 }{ 3 } )\) m and the diameter of hemisphere is 3.5 m. Calculate the volume and the internal surface area of the solid.
Solution:
Diameter of the cylindrical part = 3.5 m
∴Radius (r) = \((\frac { 3.5 }{ 2 } )\) = 1.75 = \((\frac { 7 }{ 4 } )\) m
and height (h) = \((\frac { 14 }{ 3 } )\) m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 18
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 19

Question 14.
A solid is composed of a cylinder with hemispherical ends. If the whole length of the solid is 104 cm and the radius of each of the hemispherical ends is 7 cm, find the cost of polishing its surface at the rate of Rs. 10 per dm2 . (C.B.S.E. 2006C)
Solution:
Total height = 104 cm
Radius of hemispherical part (r) = 7 cm
Height of cylinder (h) = 104 cm – 2 x 7 cm = 104- 14 = 90 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 20
Total outer surface area = curved surface area of the cylindrical part + 2 x curved surface area of each hemispherical part
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 21

Question 15.
A cylindrical vessel of diameter 14 cm and height 42 cm is fixed symmetrically inside a similar vessel of diameter 16 cm and height 42 cm. The total space between the two vessels is filled with cork dust for heat insulation purposes. How many cubic centimeters of cork dust will be required ?
Solution:
Diameter of inner cylinder = 14 cm
∴Radius (r) = \((\frac { 14 }{ 2 } )\) = 7 cm
Diameter of outer cylinder = 16 cm
∴ Radius (R) = \((\frac { 16 }{ 2 } )\) = 8 cm
Height (h) = 42cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 22

Question 16.
A cylindrical road roller made of iron is 1 m long. Its internal diameter is 54 cm and the thickness of the iron sheet used in making the roller is 9 cm. Find the mass of the roller, if 1 cm³ of iron has 7.8 gm mass. (Use π = 3.14)
Solution:
Length of roller (h) = 1 m = 100 cm
Inner diameter = 54 cm
Thickness of iron sheet = 9 cm
∴ Inner radius (r) = \((\frac { 52 }{ 2 } )\) = 27 cm
and outer radus (R) = 27 + 9 = 36 cm
∴ Volume of the mass = πR²h – πr²h
= πh (R²- r²)
= 3.14 x 100 (36² – 27²) cm3
= 314 x (36 + 27) (36- 27) cm3
= 314 x 63 x 9 cmc
= 178038 cm3
Weight of 1 cm3 of iron = 7.8 gm
∴ Total weight = 178038 x 7.8 gm
= 1388696.4 gm
= 1388.6964 kg
= 1388.7 kg

Question 17.
A vessel in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
Solution:
Diameter of hemisphere = 14 cm
Total height =13 cm
Radius of hemisphere = \((\frac { 14 }{ 2 } )\) = 7 cm
∴ Height of cylindrical part =13-7 = 6 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 23
∴  Inner surface area of the vessel = inner surface area of cylindrical part + inner surface area of hemispherical part
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 24

Question 18.
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Solution:
Radius of cone (r) – 3.5 cm
Total height of the toy = 15.5 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 25
Height of the conical part (h) = 15.5 – 3.5 = 12 cm
∴ Slant height of the cone (l)
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 26

Question 19.
The difference between outside and inside surface areas of cylindrical metallic pipe 14 cm long is 44 m2. If the pipe is made of 99 cm3 of metal, find the outer and inner radii of the pipe.
Solution:
In cylindrical metallic pipe,
length of pipe = 14 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 27
Difference between outside and inside
surface area = 44 m2
Volume of pipe material = 99 cm3
Let R and r be the outer and inner radii of the pipe respectively, then Outer surface area – inner surface area = 44 cm2
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 28

Question 20.
A right circular cylinder having diameter 12 cm and height 15 cm is full ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
Solution:
Height of cylinder (H) = 15 cm
and diameter =12 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 29
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 30

Question 21.
A solid iron pole having cylindrical portion 110 cm high and of base diameter 12 cm is surmounted by a cone 9 cm high. Find the mass of the pole, given that the mass of 1 cm3 of iron is 8 gm.
Solution:
Diamter of the base = 12 cm
∴ Radius (r) = \((\frac { 12 }{ 2 } )\) = 6 cm
Height of the cylindrical portion (h1)= 110 cm
and height of conical portion (h2) = 9 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 31
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 32

Question 22.
A solid toy is in the form of a hemisphere surmounted by a right circular cone. Height of the cone is 2 cm and the diameter of the base is 4 cm. If a right circular cylinder circumscribes the toy, find how much more space it will cover.
Solution:
Height of conical part (h) = 2 cm
Diameter of base = 4 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 33
Now volume of the cylinder which circum scribes the toy = πr²h
= π (2)² x 4 = 16π cm³
∴  Difference of their volumes = 16π – 8π = 8πcm³

Question 23.
A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottoms. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
Solution:
Radius of conical part = 60 cm
and height (h) = 120 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 34
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 35

Question 24.
A cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water. Find the value of water (i) displaced out of the cylinder. (ii) left in the cylinder. (C.B.S.E. 2009)
Solution:
Internal diameters of cylindrical vessel = 10 cm
∴ Radius (r) = \((\frac { 10 }{ 2 } )\) =5 cm
and height (h) = 10.5 cm
∴ Volume of water filled in it
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 36

Question 25.
A hemispherical depression is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to the edge of the cube. Determine the volume and total surface area of the remaining block. [CBSE 2010]
Solution:
Edge of cube = 21 cm
∴ Diameter of the hemisphere curved out of
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 37

Question 26.
A toy is in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of the hemisphere. If the radius of the base of the cone is 21 cm and its volume is 2/3 of the volume of the hemisphere, calculate the height of the cone and the surface area of the toy. (Use π = 22/7).
Solution:
Radius of base of the conical part (r) = 21 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 38
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 39

Question 27.
A solid is in the shape of a cone surmounted on a hemi-sphere, the radius of each of them is being 3.5 cm and the total height of solid is 9.5 cm. Find the volume of the solid. [CBSE 2012]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 40
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 41

Question 28.
An wooden toy is made by scooping out a hemisphere of same radius from each end of a solid cylinder. If the height of the cylinder is 10 cm, and its base is of radius
3.5 cm, find the volume of wood in the toy. (Use π = 22/7). [CBSE 2013]
Solution:
Height of cylindrical part (h) = 10 cm
Radius of the base (r) = 3.5 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 42

Question 29.
The largest possible sphere is carved out of a wooden solid cube of side 7 cm. Find the volume of the wood left. (Use π = 22/7). [CBSE 2014]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 43

Question 30.
From a solid cylinder of height 2.8 cm and diameter 4.2 cm, conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid, (take π = 22/7). [CBSE 2014]
Solution:
Diameter of solid cylinder= 4.2 cm
∴ Radius (r) =\((\frac { 4.2 }{ 2 } )\) = 2.1 cm
Height (h) = 2.8 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 44

Question 31.
The largest cone is curved out from one face of solid cube of side 21 cm. Find the volume of the remaining solid. [CBSE 2015]
Solution:
Side of a solid cube (a) = 21 cm
∴ Volume = a3, = (21 )3 cm3
= 9261 cm3
Diameter of the base of cone = 21 cm
Now radius of cone curved from it (r) =\((\frac { 21 }{ 2 } )\) cm
and height (h) = 21 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 45

Question 32.
A solid wooden toy is in the form of a hemisphere surmounted by a Cone of same radius. The radius of hemisphere is 3.5 cm and the total wood used in the making of toy is 166 \((\frac { 5 }{ 6 } )\) cm3 . Find the height of the toy. Also, find the cost of painting the hemispherical part of the toy at the rate of ₹10 per cm2. (Take π  = 22/7). [CBSE 2015]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 46
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 47

Question 33.
In the given figure, from a cuboidal solid metalic block, of dimensions 15 cm x 10 cm x 5 cm, a cylindrical hole of diameter 7 cm is drilled out. Find the surface area of the remaining block. (Take  π = 22/7) [CBSE 2015]
Solution:
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 48
Radius of hole = \((\frac { 7 }{ 2 } )\)cm and height = 5 cm
Length of block (l) = 15 cm
Breadth (b) = 10 cm and height = 5 cm
∴ Surface area = 2(lb + bh + hl)
= 2(15 x 10 + 10 x 5 + 5 x 15) cm2
= 2(150 + 50 + 75) = 2 x 275 = 550 cm2
Area of circular holes of both sides = 2 x πr2
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 49

Question 34.
 A building is in the form of a cylinder surmounted by a hemi-spherical vaulted dome and
contains 41 \((\frac { 19 }{ 21 } )\) m3 of air. If the internal diameter of dome is equal to its total height above the floor, find the height of the building? [NCERT Exemplar]
Solution:
Let total height of the building = Internal diameter of the dome = 2rm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 50
Radius of building (or dome) = \((\frac { 2r }{ 2 } )\) = r m
Height of cylinder = 2r-r = rm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 51

Question 35.
A pen stand made of wood is in the shape of a cuboid with four conical depressions and a cubical depression to hold the pens and pins, respectively. The dimension of the cuboid are 10 cm x 5 cm x 4 cm. The radius of each of the conical depression is 0.5 cm and the depth is 2.1 cm. The edge of the cubical depression is 3 cm. Find the volume of the wood in the entire stand. [NCERT Exemplar]
Solution:
Given that, length of cuboid pen stand (l) = 10 cm
Breadth of cuboid pen stand (b) = 5 cm
and height of cuboid pen stand (h) = 4 cm
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 52
∴ Volume of cuboid pend stand = l x b x h= 10 x 5 x 4 = 200 cm3
Also, radius of conical depression (r) = 0.5 cm
and height (depth) of a conical depression (h1) = 2.1 cm
∴ Volume of a conical depression = πrh1
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 53

Question 36.
 A building is in the form of a cylinder surmounted by a hemispherical dome. The base diameter of the dome is equal to \((\frac { 2 }{ 3 } )\) of the total height of the building. Find the height of the building, if it contains 67 \((\frac { 1 }{ 21 } )\) m3 of air.
Solution:
Let the radius of the hemispherical dome be r metres and the total height of the building be h metres.
Since the base diameter of the dome is equal to \((\frac { 2 }{ 3 } )\) of the total height, therefore
2 r = \((\frac { 2 }{ 3 } )\)h. This implies r = \((\frac { h }{ 3 } )\). Let H metres be the height of the cylindrical portion.
Therefore, H = h – \((\frac { h }{ 3 } )\) = \((\frac { 2 }{ 3 } )\)h metres.
Volume of the air inside the building = Volume of air inside the dome + Volume of the air inside the
cylinder = \((\frac { 2 }{ 3 } )\) πr3 + πr2H, where H is the height of the cylindrical portion
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 54

Question 37.
A solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of cone is 4 cm and the diameter of the base is 8 cm. Determine the volume of the toy. If a cube circumscribes the toy, then find the difference of the volumes of cube and the toy. Also, find the total surface area of the toy. [NCERT Exemplar]
Solution:
Let r be the radius of the hemisphere and the cone and h be the height of the cone.
Volume of the toy=Volume of the hemisphere + Volume of the cone
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 55

= \((\frac { 1408 }{ 7 } )\) cm3
A cube circumsrcibes the given solid. Therefore, edge of the cube should be 8 cm. Volume of the cube = 83 cm3 = 512 cm3 Difference in the volume of the cube and
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 56

Question 38.
A circus tent is in the shape of a cylinder surmounted by a conical top of same diameter. If their common diameter is 56 m, the height of the cylindrical part is 6 m and the total height of the tent above the ground is 27 m, find the area of the canvas used in making the tent. [ICBSE 2017]
Solution:
We have, diameter of base of cylinder = d = 56 m
Radius of base of cylinder = r=  \((\frac { d }{ 2 } )\)=  \((\frac { 52 }{ 2 } )\)= 28 m
Height of tent = 27 m
Height of cylinder = 6 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 57
Height of conical portion = 27 – 6 = 21 m
Radius of conical portion, r = 28 m
RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 58

Hope given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

CA Foundation Business Economics Study Material – Basic Problems of an Economy and Role of Price Mechanism

CA Foundation Business Economics Study Material Chapter 1 Nature and Scope of Business Economics – Basic Problems of an Economy and Role of Price Mechanism

Basic Problems of an Economy

  • We know that human wants are unlimited and resources are scarce.
  • The problem of scarcity of resources is not only faced by individuals but also by the society at large.
  • This gives rise to the problem of how to use scare resources so as to serve best the needs of the society.
  • This economic problem is to be dealt with in all the economic systems whether capitalist or socialist or mixed.
  • The central problems relating to allocation of resources are:
    • What to produce and how much to produce?
    • How to produce?
    • For whom to produce?
    • What provision should be made for economic growth?

What to produce and how much to produce?

  • An economy has millions commodities to produce.
  • It has to decide what commodities are to be produced and how much.
  • E.g. – To produce luxury goods or consumer goods, etc.
  • Here, the guiding principle is to allocate the resources in the production of goods in such a way that maximizes aggregate utility.

How to produce ?

  • There are many alternative techniques to produce a commodity. ‘
  • Choice has to be made between capital intensive technique or labour intensive technique of production.
  • The choice of technique will depend upon —
    • availability of various factors of production, &
    • the prices of factors of production.
  • Such techniques of production has to be adopted that makes best use of available resources.

For whom to produce?

  • Who will consume the goods and services that are produced in the economy?
  • Whether a few rich or many poor will consume?
  • Goods and services are produced for those people who can purchase them or pay for them.
  • Paying capacity depends upon income or purchasing power.

What provisions should be made for economic growth?

  • A society cannot afford to use all its scarce resources for current consumption only.
  • It has to provide for the future as well so that high economic growth can be achieved.

Therefore, an economy has to take decisions about rate of savings, investment, capital formation, etc.

Meaning of Economic System

An economic system comprises the totality of forms through which the day to day economic process is at work. It refers to the mode of production, exchange, distributions and the role which government play in economic activity. There are three types of economic systems Capitalism, Socialism and Mixed Economy ‘

CAPITALIST ECONOMY

  • Capitalistic economic systems is one in which all the means of production are privately owned.
  • The owners of property, wealth and capital are free to use them as they like in order to earn profits.
  • The central problems about what, how and for whom to produce are solved by the free play of market forces.

Characteristics of Capitalist Economy:

  • There is right to own and keep private property by individuals. People have a right to acquire, use, control, enjoy or dispose off it as they like.
  • There is right of inheritance ie. transfer of property of a person to his legal heirs after his death.
  • There is freedom of enterprise ie. everybody is free to engage in any type of economic activity he likes.
  • There is freedom of choice by consumers ie. consumer is free to spend his income on whatever goods or services he wants to buy and consume.
  • Entrepreneurs or producers in their productive activity are guided by their profit motive. Thus profit motive is the guiding force behind all the productive activity.
  • There is stiff competition among sellers or producers of similar goods. There is competition among all the participants in the market.
  • Price mechanism is an important feature of capitalist economy were the price is determined through the interaction of market forces of demand and supply.

Merits of Capitalist Economy:

  • Capitalism works through price mechanism and hence self regulating
  • In capitalism there is greater efficiency and incentive to work due to two motivating force namely private property and profit motive.
  • Faster economic growth is possible.
  • There is optimum allocation of productive resources of the economy.
  • There is high degree of operative efficiency.
  • Cost effective methods are employed in order to maximise profits.
  • Consumers are benefited as large range of quality goods at reasonable prices are available from which they makes the choice. This also results in higher standard of living.
  • In capitalism there is more innovations and technological progress and country benefits from research and development, growth of business talent, etc.
  • Fundamental rights like right to private property and right to freedom are preserved.
  • It leads to emergence of new entrepreneurial class who is willing to take risks.

Demerits of Capitalist Economy:

  • In capitalism there is vast economic inequality and social injustice which reduces the welfare of the society.
  • There is precedence of property rights over human rights.
  • Cut-throat competition and profit motive work against consumer welfare leading to exploitation of consumers.
  • There are wastage of resources due to duplication of work and cut-throat competition.
  • Income inequalities lead to differences in economic opportunities. This lead to rich becoming richer and poor becoming poorer.
  • There is exploitation of labour.
  • More of luxury goods and less of wage goods are produced leading to misallocation of resources. .
  • Unplanned production, economic instability in terms of over production, depression, unemployment, etc. are common in a capitalist economy.
  • Leads to creation of monopolies.
  • Ignores human welfare because main aim is profit.

SOCIALIST ECONOMY

The concept of socialism was given by Karl Marx and Frederic Engels in their work ‘The Communist Manifesto’ published is 1848. A socialist economy is also called as “Command Economy” or a “Centrally Planned Economy.”

  • In a socialist economy, all the property, wealth and capital is owned by State. There is no private property.
  • State organises all economic activities. It owns, controls and manages the production units; it distributes the goods among the consumers; it decides the size and direction of investment.
  • The state works for the welfare of the people and not for profit.

Characteristics of Socialist Economy:

  • There is collective ownership of means of production Le. all the important means of production are state owned.
  • It is a centrally planned economy. All the basic decisions relating to the working and the regulation of the economy are taken by central authority called planning commission.
    • Production and distribution of goods is ensured through planning on preferences deter-mined by the state. So freedom from hunger is guaranteed but, consumer’s sovereignty is restricted.
  • There is social welfare in place of profit motive. Those goods and services are given top priority which is in the interest of largest number of people.
    • Price policy is guided by the aims of social welfare than profit motive.
  • There is lack of competition because it avoid duplication of efforts and wastage of resources. Hence, competition is done away.
  • Socialism tries to ensure equitable distribution of income through equality of opportunities. Thus, right to work is guaranteed but choice of occupation is restricted.

Merits of Socialist Economy:

  • Social justice is maintained by equitable distribution of income and wealth and by providing equal opportunities to all.
  • Balanced economic development is possible. Central planning authority allocate resources according to the plans and priorities.
  • There are no class conflict and community develops a co-operative mentality.
  • Unemployment is minimized, business fluctuations are eliminated resulting in stability.
  • Right to work is ensured and minimum standard of living is maintained.
  • There is no exploitation of consumers and workers.
  • Wastage of resources are avoided due to planning resulting in better utilization of resources and maximum production.
  • Citizens feel secure as there is social security cover for them.
  • Demerits of Socialist Economy:
  • There is predominance of bureaucracy resulting in inefficiency and delays.
  • There is no freedom of individuals as it takes away basic rights also like right of private property.
  • Workers are not paid according to their personal efficiency and productivity. This acts as disincentive to work hard.
  • Prices are administered by the state.
  • State monopolies may be created and may become uncontrollable. This will be more dan¬gerous than monopolies under capitalism.
  • The consumers have no freedom of choice.

MIXED ECONOMY

Mixed economy combines the features of both capitalism and socialism. The concept is designed to incorporate best of both. The main characteristics/features are:—

  • There is co-existence of both private and public sector ie. economic resources are owned by individuals and state.
    • State open those enterprises which are in the interest of the’society as a whole.
    • Private sector moves to those enterprises which produce higher profit.
  • There is co-existence of free price mechanism and economic planning.
    • Price mechanism is however curtailed through measures like price control, administered prices etc.
    • Planning is done through incentives like concessions, subsidies, etc. and disincentives like high rate of taxes, strict licensing etc.
  • In mixed economy social welfare motive gets due importance particularly in case of poor and backward classes.
    Eg. Subsidised hospital, food articles, education etc.; social security schemes like old age pension, reservation of jobs, laws in the interest of workers, consumers, human, children etc.
  • There is freedom to joint any occupation, trade or service according to the education, training, skills and ability.
  • There is freedom of consumption. People are free to consume goods and services of their choice and in the quantity they can afford.

Merits of Mixed Economy:

  • Merits of capitalist economy and socialist economy are found in mixed economy.
  • There is right of private property and economic freedom. This results in incentive to work hard and capital formation.
  • Price mechanism and competition induces the private sector in efficient decision making and better resource allocation.
  • There is freedom of occupation and consumption.
  • Encourages enterprise and risk taking.
  • Leads to development of technologies through research and development.
  • Economic and social equality is more.

However, mixed economy suffers from uncertainties, excess control by state, poor implementation of plans, high taxes, corruption, wastage of resources, slow growth, lack of efficiency, etc. There are possibilities of private sector growing, disproportionately if state does not maintain a proper balance between public and private sectors.

CA Foundation Business Economics Study Material – Nature and Scope of Business Economics

CA Foundation Business Economics Study Material – Nature and Scope of Business Economics

Nature of Business Economics

The subject matter of Economics is broadly divided into two major parts namely:—
Micro-Economics, and Macro-Economics
Before dealing with nature of Business Economics, it is necessary to understand the difference between the two.

1. Micro-Economics – Micro means a ‘small part’. Therefore, Micro-economics study the behaviour of small part or a small component or different individuals and organisations of a national economy. It examines how the individual units take decision about rational allocation of their scarce resources.

Micro-Economics covers the following:

  • Theory of Product Pricing;
  • Theory of Consumer Behaviour,
  • Theory of Factor Pricing;
  • The economic conditions of a section of people;
  • Behaviour of firms; and
  • Location of industry.

2. Macro-Economics – Macro means ‘large’. Therefore, macro-economics deals with the large economic activity. It study the economic system of a country as a whole ie. overall condition of an economy. It is a study of large aggregates like total employment, the general price level. Total output, total consumption, total saving and total investments. It also analyses how these aggregates change over time.

Macro-Economics covers the following:

  • National Income and National Output;
  • The General Price Level and interest rates;
  • Balance of Trade and Balance of Payments;
  • External value of currency ie. exchange rate;
  • Overall level of savings and investments ie. capital formation; and
  • The level of employment and rate of economic growth.

Business Economics is primarily concerned with Micro-Economics. However, knowledge and understanding of Macro-economic environment is also necessary. This is because macro-economic environment influence individual firm’s performance and decisions.

As already seen Business Economics enables application of economic knowledge, logic, theories and analytical tools. It is Applied Economics that fills the gap between economic theory and business practice. The following will describe the nature of Business Economics:

  1. Business Economics is a Science: Science is a systematised body of knowledge which trace the cause and effect relationships. Business Economics uses the tools of Mathematics, Statistics and Econometrics with economic theory to take decisions and frame strategies. Thus, it makes use of scientific methods.
  2. Based on Micro-Economics: As Business Economics is concerned more with the decision making problems of a particular business establishment. Micro level approach suits is more. Thus, Business Economics largely depends on the techniques of Micro-Economics.
  3. Incorporates elements of Macro Analysis: A business unit is affected by external environment of the economy in which it operates. A business units is affected by general price level, level of employment, govt, policies related to taxes, interest rates, industries, exchange rates, etc. A business manager should consider such macro-economic variables which may affect present or future business environment.
  4. Business Economics is an Art: It is related with practical application of laws and principles to achieve the objectives.
  5. Use of Theory of Markets & Private Enterprise: It uses the theory of markets and resource allocation in a capitalist economy.
  6. Pragmatic Approach: Micro-Economics is purely theoretical while, Business Economics is practical in its approach.
  7. Inter-disciplinary in nature: It incorporates tools from other disciplines like Mathematics, Statistics, Econometrics, Management Theory, Accounting, etc.
  8. Normative in Nature: Economic theory has been developed along two lines – POSITIVE and NORMATIVE.

A positive science or pure science deals with the things as they are and their CAUSE and EFFECTS only. It states ‘what is’? It is DESCRIPTIVE in nature. It does not pass any moral or value judgments.

A normative science deals with ‘what ought to be’ or ‘what should be’. It passes value judgments and states what is right and what is wrong. It is PRESCRIPTIVE in nature as it offers suggestions to solve problems. Normative science is more practical, realistic and useful science.

Business Economics is normative in nature because it suggests application of economic principles to solve problems of an enterprise, However, firms should have clear understanding of their environment and therefore, it has to study positive theory.

Scope of Business Economics

The scope of Business Economics is wide. Economic theories can be directly applied to two types of business issues namely—

  1. Micro-economics is applied to operational or internal issues off a firm.
  2. Macro-economics is applied to environment or external issues on which the firm has no control.

1. Micro-economics applied to operational or internal issues
Issues like choice of business size of business, plant layout, technology, product decisions, pricing, sales promotion, etc. are dealt by Micro-economic theories. It covers—

  • Demand analysis and forecasting
  • Production and Cost Analysis
  • Inventory Management
  • Market Structure and Pricing Analysis
  • Resource Allocation
  • Theory of Capital and Investment Decisions
  • Profitability Analysis
  • Risk and Uncertainty Analysis.

2. Macro-economics applied to environmental or external issues
The major economic factors relate to—

  • the type of economic system
  • stage of business cycles
  • the general trends in national income, employment, prices, saving and investment.
  • government’s economic policies
  • working of financial sector and capital market
  • socio-economic organisations
  • social and political environment.

These external issues has to be considered by a firm in business decisions and frame its policies accordingly to minimize their adverse effects.