Prasanna

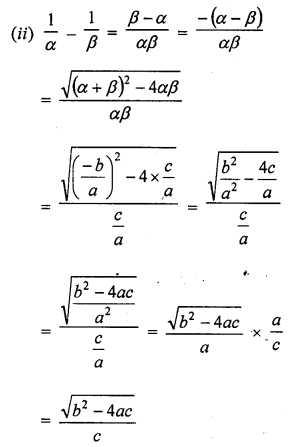
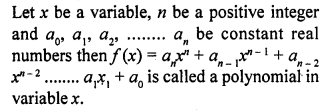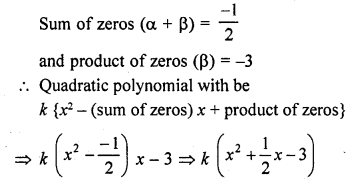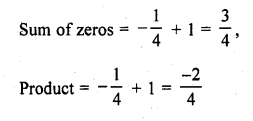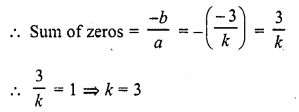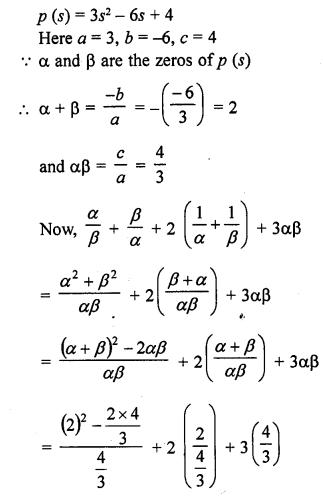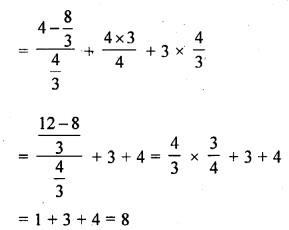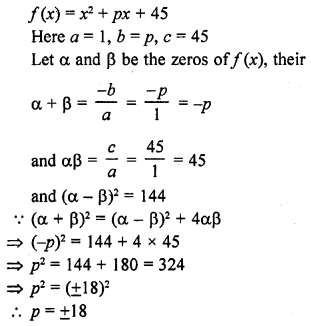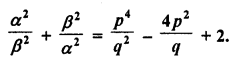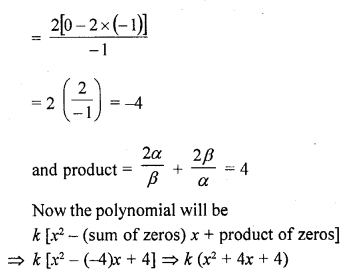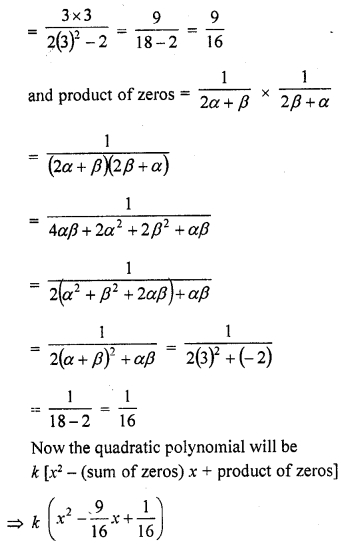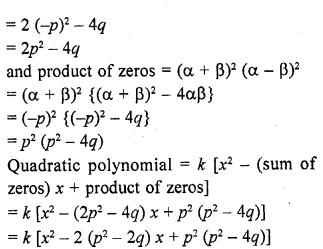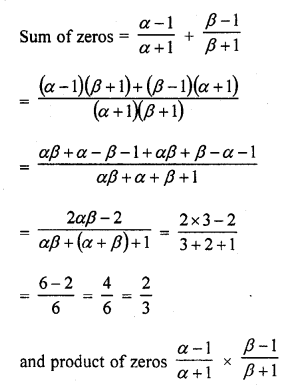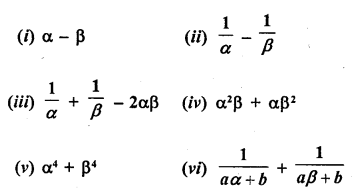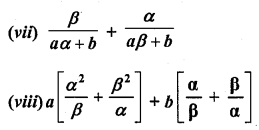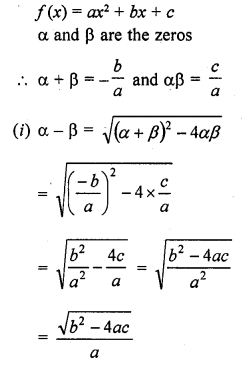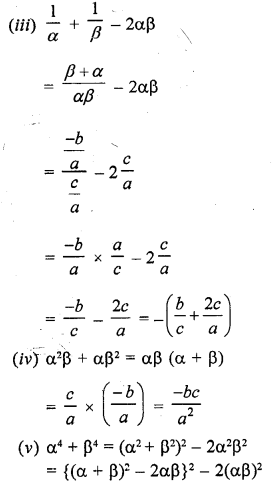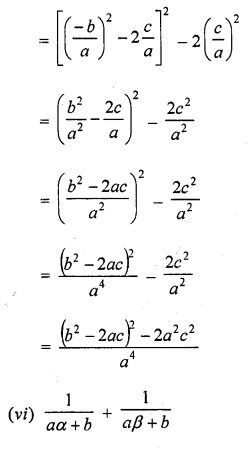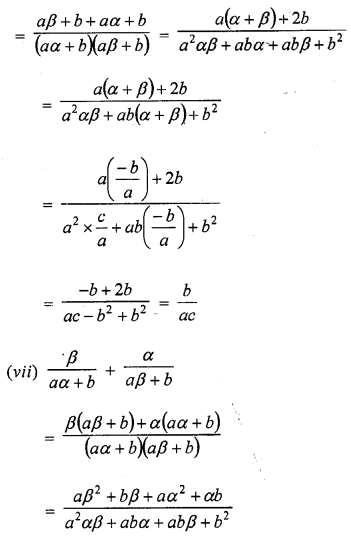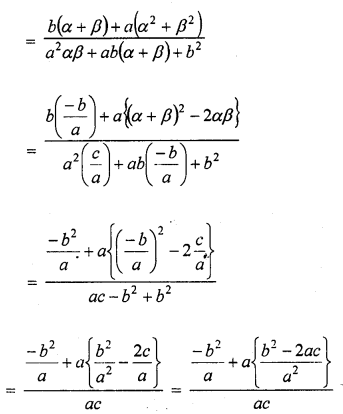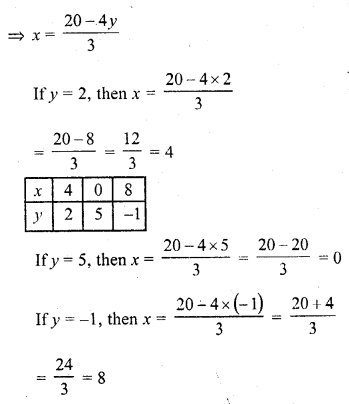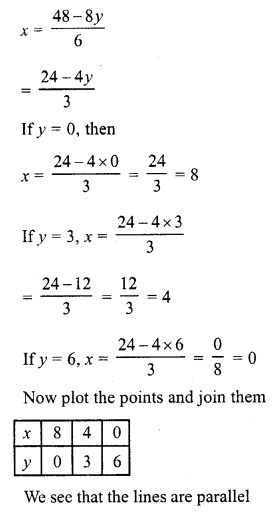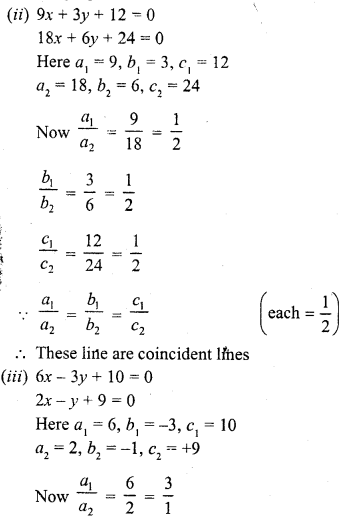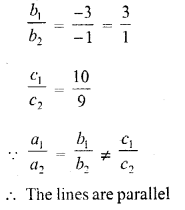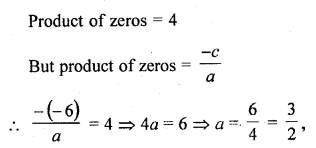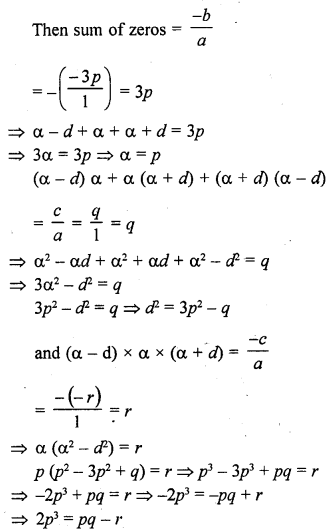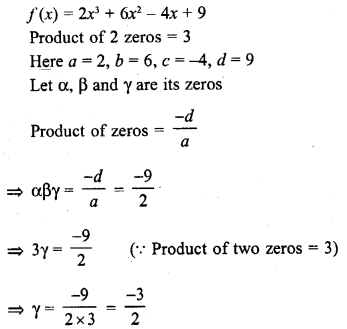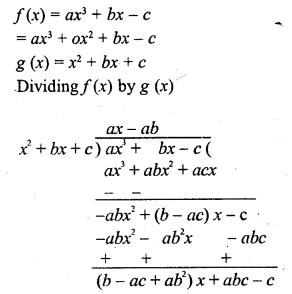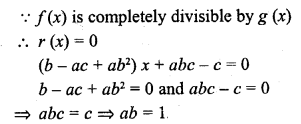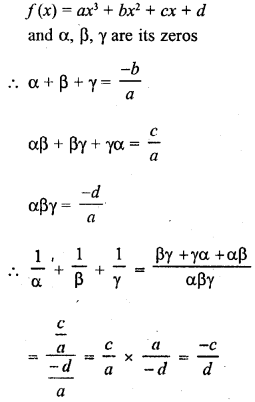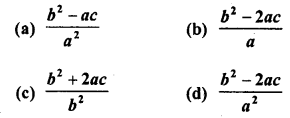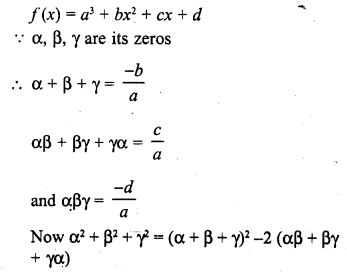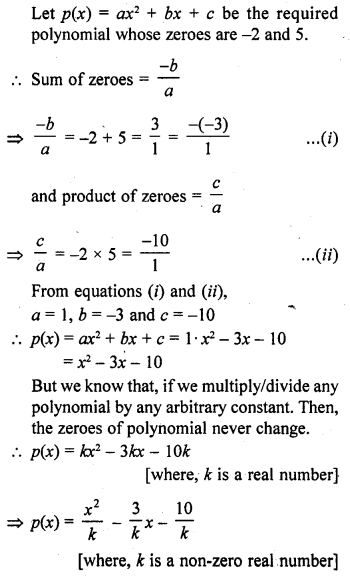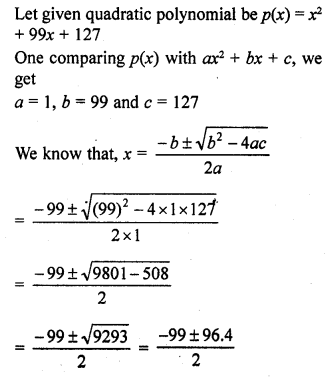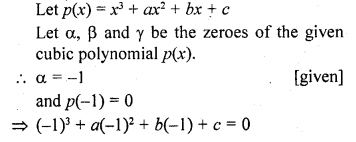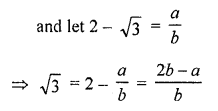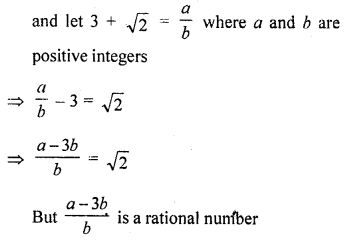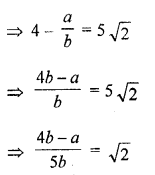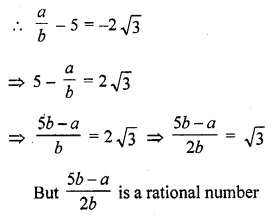RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

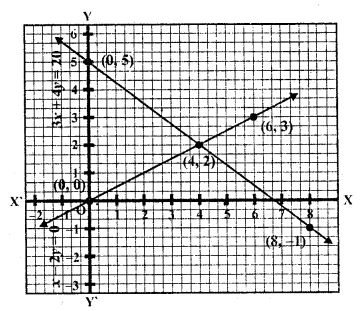
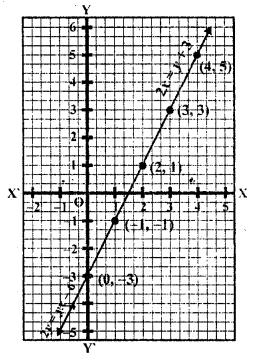
Solve the following systems of equations graphically :
Question 1.
x + y = 3
2x + 5y = 12 (C.B.S.E. 1997)
Solution:
x + y = 3
=> x = 3 – y
Substituting some different values of y, we get the corresponding values of x as shown below

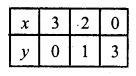
Now plot the points on the graph and join them 2x + 5y = 12
2x = 12 – 5y
⇒ x = \(\frac { 12-5y }{ 2 }\)
Substituting some different values of y, we get the corresponding values of x as shown below

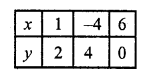
Now plot the points on the graph and join them we see that these two lines intersect each other at (1, 2)
x = 1, y = 2

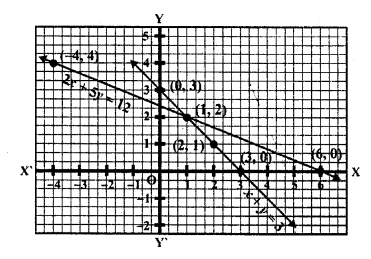
Question 2.
x – 2y = 5
2x + 3y = 10 (C.B.S.E. 1997)
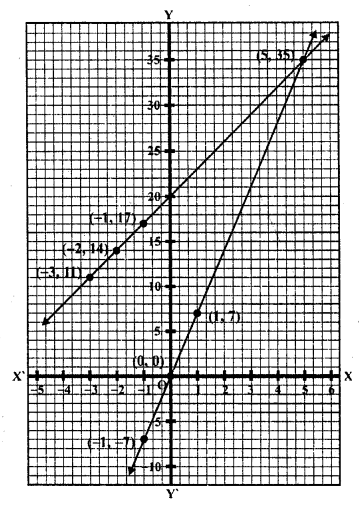
Solution:
x – 2y = 5 => x = 5 + 2y
Substituting some different values of y, we get the corresponding values of x as shown below

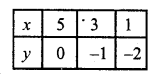
Now plot the points are the graph and join them
2x + 3y = 10 => 2x = 10 – 3y
⇒ x = \(\frac { 10-3y }{ 2 }\)
Substituting some different values of y We get the corresponding values of x as shown below :

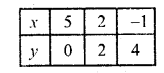
Now plot the points on the graph and join them we see that these two lines intersect each other at (5, 0)
x = 5, y = 0

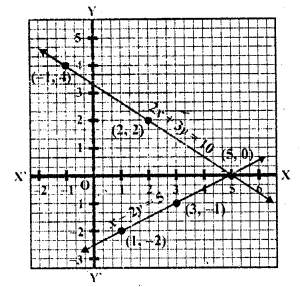
Question 3.
3x + y + 1 = 0
2x – 3y + 8 = 0 (C.B.S.E. 1996)
Solution:
3x + y + 1 = 0
y = -3x – 1
Substituting the values of x, we get the corresponding values of y, as shown below

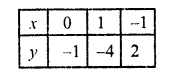
Now plot the points on the graph and join them
2x – 3y + 8 = 0
⇒ 2x = 3y – 8
⇒ x = \(\frac { 3y-8 }{ 2 }\)
Substituting some different values of y, we get the corresponding values of x as shown below

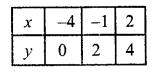
Now plot the points on the graph and join then we see that these two lines intersect, each other at (-1, -2)
x = -1, y = 2

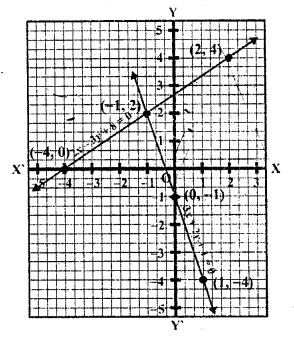
Question 4.
2x + y – 3 = 0
2x – 3y – 7 = 0 (C.B.S.E. 1996)
Solution:
2x + y – 3 = 0 => y = -2x + 3
Substituting some different values of x, we get the corresponding values of y as shown below:

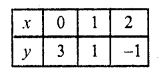
Now plot the points and join them 2x – 3y – 7 = 0
2x = 3y +7
x = \(\frac { 3y+7 }{ 2 }\)
Substituting some different values of y, we get corresponding values of x as shown below:

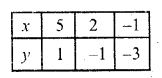
Now plot the points on the graph and join them we see that these two lines intersect each other at (2, -1)

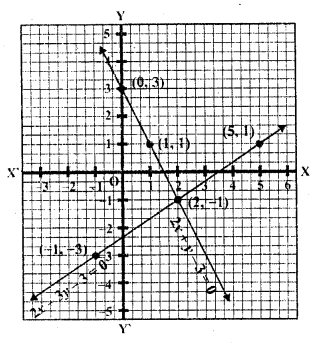
Question 5.
x + y = 6
x – y = 2 (C.B.S.E. 1994)
Solution:
x + y = 6 => x = 6 – y
Substituting some different values of y, we get the corresponding values of x as shown under

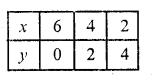
Now plot the points on the graph and join them
x – y = 2 ⇒ x = 2 + y
Substituting some different values of y, we get the corresponding values of x as shown below:

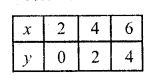
Now plot the points on the graph and join them
We see that there two lines intersect each other at (4, 2)
x = 4, y = 2

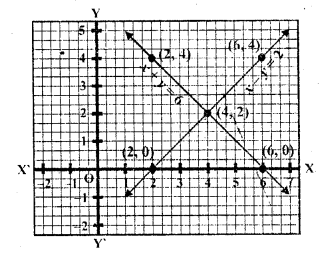
Question 6.
x – 2y = 6
3x – 6y = 0 (C.B.S.E. 1995)
Solution:
x – 2y = 6
x = 6 + 2 y
Substituting some different values ofy, we get the corresponding values of x as shown below:

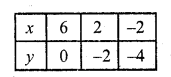
Now plot the points and join them
3x – 6y = 0 ⇒ 3x = 6y ⇒ x = 2y
Substituting some different value of y, we get corresponding the values of x as shown below:

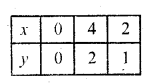
plot the points on the graph and join them We see that these two lines intersect each other at no point
The lines are parallel
There is no solution

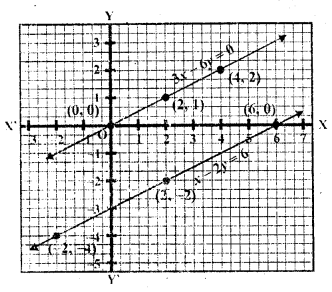
Question 7.
x + y = 4
2x – 3y = 3 (C.B.S.E. 1995)
Solution:
x + y = 4 => y = 4 – x
Substituting some different values of y, we get the corresponding values of x as shown below:

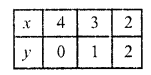
Now plot the points and join them 2x – 3y = 3
⇒ 2x = 3 + 3y
⇒ x = \(\frac { 3+3y }{ 2 }\)
Substituting some different values of y, we get the corresponding values of x as shown below:

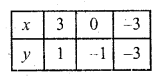
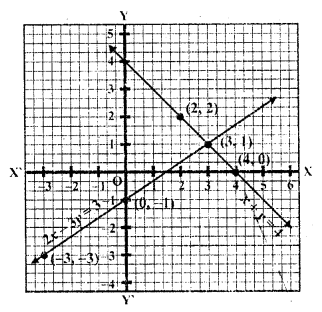
Now plot the points on the graph and join them we see that these two lines intersect each other at (3, 1)
x = 3, y = 1

Question 8.
2x + 3y= 4
x – y + 3 = 0 (C.B.S.E. 1995)
Solution:
2x + 3y = 4
=> 2x = 4 – 3y
=> x = \(\frac { 4-3y }{ 2 }\)
Substituting some different values of y, we get corresponding values of x as shown below:

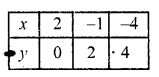
Now plot the points are the graph and join them
x – y + 3 = 0
x = y – 3
Substituting some different values of y, we get corresponding values of x as shown below:

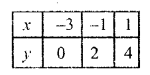
Now plot the points on the graph and join them
We see that these two lines intersect each other at (-1, 2)
x = -1, y = 2

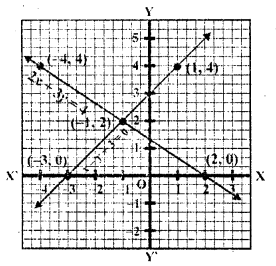
Question 9.
2x – 3y + 13 =0
3x – 2y + 12 = 0 (C.B.S.E. 2001C)
Solution:
2x – 3y + 13 = 0
2x = 3y – 13
=> x = \(\frac { 3y – 13 }{ 2 }\)
Substituting some different values of y, we get corresponding values of x as shown below

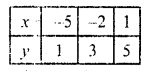
Plot the points on the graph and join them 3x – 2y + 12 = 0
3x = 2y – 12
x = \(\frac { 2y – 12 }{ 3 }\)
Substituting some different values of y, we get corresponding values of x as shown below

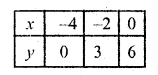
Plot the points and join them We see that these two lines intersect each other at (-2, 3)
x = -2, y = 3

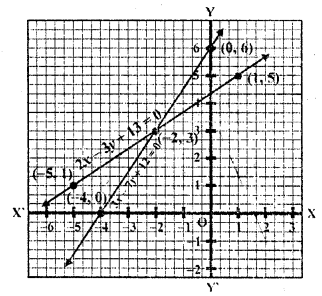
Question 10.
2x + 3y + 5 = 0
3x – 2y – 12 = 0 (C.B.S.E. 2001 C)
Solution:
2x + 3y + 5 = 0
2x = – 3y – 5
x = \(\frac { – 3y – 5 }{ 2 }\)
Substituting some different value of y, we get corresponding values of x as shown below

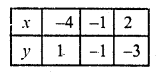
Now plot the points on the graph and join them
3x – 2y – 12 = 0
3x = 2y +12
x = \(\frac { 2y +12 }{ 3 }\)
Substituting some different value of y, we get corresponding values of x as shown below:

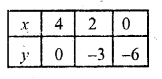
Now plot the points on the graph and join them we see that these lines intersect each other at (2, -3)
x = 2, y = -3

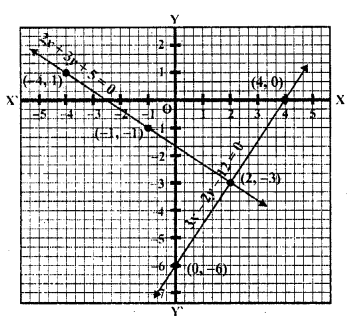
Show graphically that each one of the following systems of equations has infinitely many solutions :

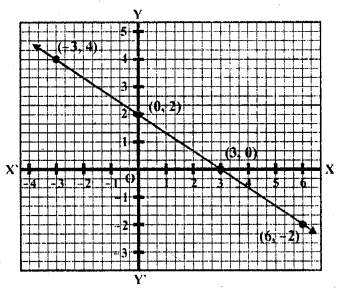
Question 11.
2x + 3y = 6
4x + 6y = 12 [CBSE2010]
Solution:
2x + 3y = 6 ……….(i)
4x + 6y = 12 ……….(ii)
2x = 6 – 3y

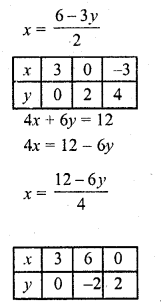
Now plot the points of both lines on the graph and join them, we see that all the points lie on the same straight line
This system has infinitely many solutions

Question 12.
x – 2y = 5
3x – 6y = 15
Solution:
x – 2y = 5
x = 5 + 2y
Substituting some different values of y, we get corresponding values of x as shown below:

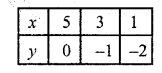
Now plot these points on the graph and join them
3x – 6y = 15
=> 3x = 15 + 6y
x = \(\frac { 15 + 6y }{ 3 }\)
Substituting some different values of y, we get corresponding values of x as shown below:

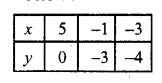
Now plot there points on the graph and join then
We see that these two lines coincide each other
This system has infinitely many solutions.

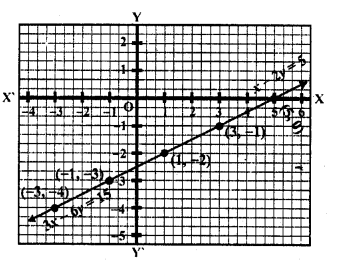
Question 13.
3x +y = 8
6x + 2y = 16
Solution:
3x + y = 8 => y = 8 – 3x
Substituting some different values of x, we get corresponding values of y as shown below:

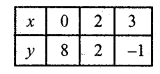
Now plot these points on the graph and join them
6x + 2y – 16 => 6x = 16 – 2y
x = \(\frac { 16 – 2y }{ 6 }\)
x = \(\frac { 8 – y }{ 3 }\) (Dividing by 2)
Substituting some different values of y, we get their corresponding values of x as shown below:

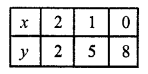
Now plot the points and point them
We see that the two lines coincide each other
This system has infinitely many solutions

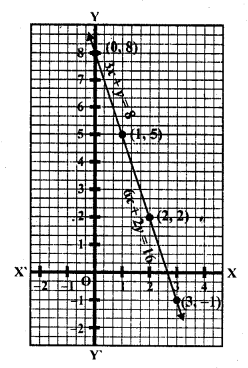
Question 14.
x- 2y + 11 = 0
3x – 6y + 33 = 0
Solution:
x – 2y + 11 = 0
x = 2y – 11
Substituting some different values of y, we get their corresponding values of x as shown below

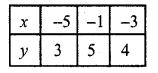
Plot the points on the graph and join them 3x – 6y + 33 = 0
3x = 6y – 33
x = \(\frac { 6y – 33 }{ 3 }\)
Substituting some different values of y, we get corresponding values of x as shown below

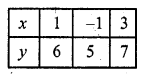
Plot the points on the graph and join them we see that the two lines coincide each other
This system has infinitely many solutions.

Show graphically that each one of the following systems of equations is inconsistent (i.e., has no solution)

Question 15.
3x – 5y = 20
6x – 10y = -40 (C.B.S.E. 1995C)
Solution:
3x – 5y = 20
3x = 20 + 5y
x = \(\frac { 20 + 5y }{ 3 }\)
Substituting some different values of y, we get their corresponding values of x as shown below

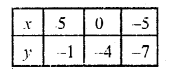
Plot the points on the graph and join them
6x – 10y = -40
6x = 10y – 40
x = \(\frac { 10y – 40 }{ 6 }\)
Substituting some different values of y, we get their corresponding values of x as shown below

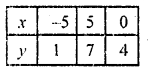
Plot the points on the graph and join them we see that the lines are parallel
The given system of equations is inconsistant and has no solution.

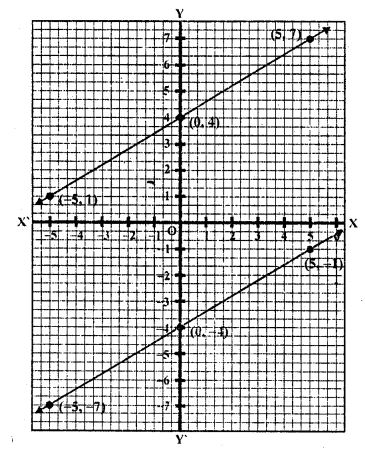
Question 16.
x – 2y = 6
3x – 6y = 0 (C.B.S.E. 1995)
Solution:
x – 2y = 6
x = 6 + 2y
Substituting some different values of y, we get their corresponding values of x as shown below:

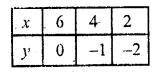
Plot the points on the graph and join them
3x – 6y = 0
=> 3x = 6y
=> x = 2y
Substituting some different values of y, we get their corresponding values of x as shown below:

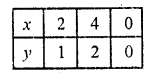
Plot the points on the graph and join them We see that the lines are parallel
The system of equation is inconsistant and therefore has no solution.

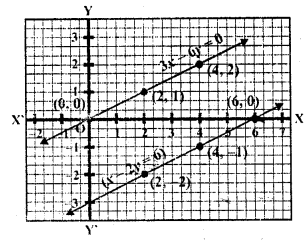
Question 17.
2y – x = 9
6y – 3x = 21 (C.B.S.E. 1995C)
Solution:
2y – x = 9
=> x = 2y – 9
Substituting some different values of y, we get their corresponding values of x as shown below:

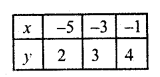
Now plot the points on the graph and join them
6y – 3x = 21
=> 6y = 21 + 3x
y = \(\frac { 21 + 3x }{ 6 }\)
Substituting some different values of x, we get their corresponding values of y as shown below:

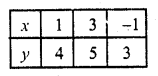
Now plot the points on the graph and join them we see that the lines are parallel
The system of equations is inconsistant and therefore has no solution.

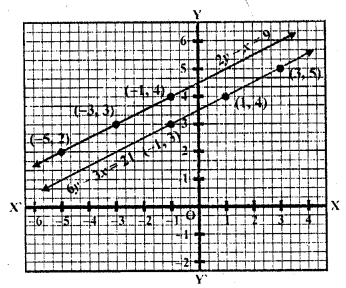
Question 18.
3x – 4y – 1 = 0
2x – \(\frac { 8 }{ 3 }\) y + 5 = 0
Solution:
3x – 4y -1 = 0
3x = 4y + 1
x = \(\frac { 4y + 1 }{ 3 }\)
Substituting some different values of y, we get their corresponding values of x as shown below:

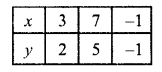
Now plot the points on the graph and join them
2x – \(\frac { 8 }{ 3 }\) y + 5 = 0
=> 6x – 8y + 15 = 0
=> 6x = 8y – 15
=> x = \(\frac { 8y – 15 }{ 6 }\)
Now substituting some different values of y, we get their corresponding values of x as shown below

Plot the points on the graph and join them We see that the lines are parallel
The system of equations is inconsistant Therefore has no solution.

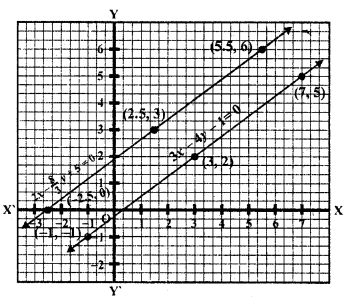
Question 19.
Determine graphically the vertices of the triangle the equations of whose sides are given below :
(i) 2y – x = 8, 5y – x = 14 and y – 2x = 1 (C.B.S.E. 1994)
(ii) y = x, y = 0 and 3x + 3y = 10 (C.B.S.E. 1994)
Solution:
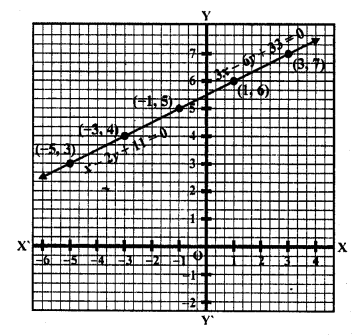
(i) Equations of the sides of a triangle are 2y – x = 8, 5y – x = 14 and y – 2x = 1
2y – x = 8
x = 2y – 8
Substituting some different values of y, we get their corresponding values of x as shown below

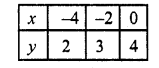
Now plot the points and join them Similarly in 5y – x = 14
x = 5y – 14

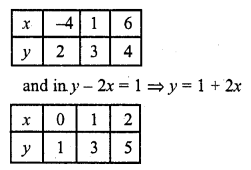
Now plot these points and join them in each case
We see that these lines intersect at (-4, 2), (1, 3) and (2, 5) which are the vertices of the triangle so formed.

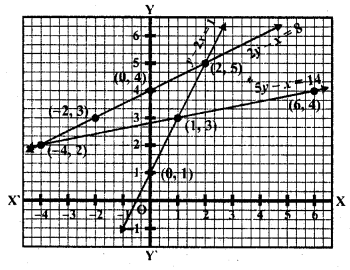
(ii) y = x, y = 0 and 3x + 3y = 10
y = x
Substituting some different values of x, we get their corresponding values of y, as shown below

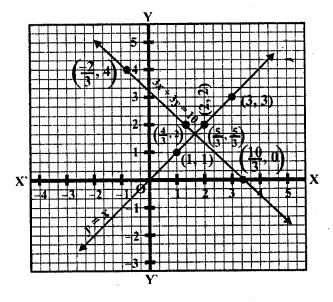
Question 20.
Determine graphically whether the system of equations x – 2y = 2, 4x – 2y = 5 is consistent or in-consistent ?
Solution:
x – 2y = 2
x = 2y + 2
Substituting some values of y, we get their corresponding values of x, as shown below

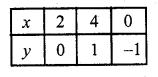
Now plot the points on the graph and join them
4x – 2y = 5
4x = 2y + 5
x = \(\frac { 2y + 5 }{ 4 }\)
Substituting some different values of y, we get their corresponding values bf x as shown below

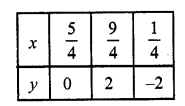
Now plot the above points and join them We see that there two lines intersect each other
The system is consistant

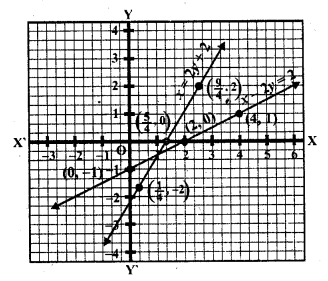
Question 21.
Determine by drawing graphs, whether the following system of linear equations has a unique solution or not :
(i) 2x – 3y = 6, x + y = 1 (C.B.S.E. 1994)
(ii) 2y = 4x – 6, 2x = y + 3 (C.B.S.E. 1995C)
Solution:
(i) 2x – 3y = 6, x + y = 1
2x – 3y = 6
=> 2x = 6 + 3y
=> x = \(\frac { 6 + 3y }{ 2 }\)
Substituting some different values of y, we get their coiTesponding values of x show below

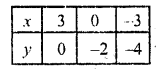
Now plot the points and join them
x + y = 1 => x = 1 – y
Substituting some different of y, we get their corresponding value of x as given below

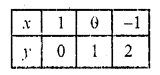
Now plot the points on the graph and join them we see that the lines intersect at a point
This system has a unique solution.

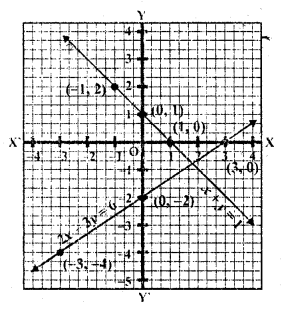
(ii) 2y = 4x – 6, 2x = y + 3
2y = 4x – 6
y = \(\frac{ 4x – 6 }{ 2 }\) = 2x – 3
Substituting some different values of x, we get their corresponding values of y as shown below

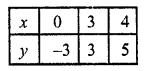
Now plot the points on the graph and join them
2x = y + 3
x = \(\frac { y + 3 }{ 2 }\)
Substituting some different values of y, we get their corresponding values of x as shown below

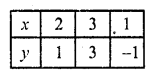
Plot the points on the graph and join them We see the lines coinside each other
This system has no unique solution.

Question 22.
Solve graphically each of the following systems of linear equations. Also And the coordinates of the points where the lines
meet axis of y.
(i) 2x – 5y + 4 = 0
2x + y – 8 = 0 (C.B.S.E. 2005)
(ii) 3x + 2y = 12
5x – 2y = 4 (C.B.S.E. 2000C)
(iii) 2x + y – 11 = 0
x – y – 1=0 (C.B.S.E. 2000C)
(iv) x + 2y – 7 = 0
2x – y – 4 = 0 (C.B.S.E. 2000C)
(v) 3x + y – 5 = 0
2x – y – 5 = 0 (C.B.S.E. 2002C)
(vi) 2x – y – 5 = 0
x – y – 3 = 0 (C.B.S.E. 2002C)
Solution:
(i) 2x – 5y + 4 = 0, 2x – 5y + 4 = 0
2x – 5y + 4 = 0 ⇒ 2x = 5y – 4
⇒ x = \(\frac { 5y – 4 }{ 2 }\)
Substituting some different values of y, we get their corresponding values of x as shown here

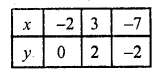
Now plot the points on the graph and join them
2x + y – 8 = 0 => 2x = 8 – y
x = \(\frac { 8 – y }{ 2 }\)
Substituting some different values of y, we get their corresponding values of x as shown below

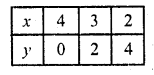
Now join these points and join them
We see that the lines intersect each other at (3, 2)
x = 3, y = 2
These line intersect y-axis at(0, \(\frac { 4 }{ 5 }\)) and (0, 8) respectively.

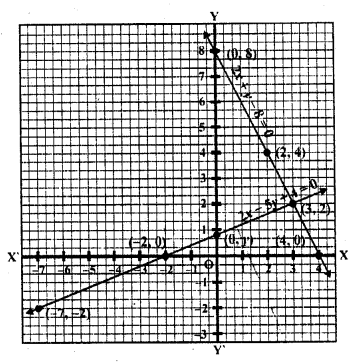
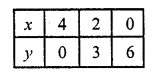
(ii) 3x + 2y = 12, 5x – 2y = 4
3x + 2y = 12
=> 3x = 12 – 2y
x = \(\frac { 12 – 2y }{ 3 }\)
Substituting some different values of y, we get their corresponding values of x as shown below

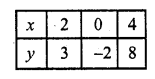
Now plot the points and join them Similarly in 5x – 2y = 4
=> 5x = 4 + 2y
x = \(\frac { 4 + 2y }{ 5 }\)

Now join these points and join them
We sec that these lines intersect each other at (2, 3)
x = 2, y= 3
There lines intersect y-axis at (0, 6) and (0, 2) respectively.

(iii) 2x + y – 11 = 0, x – y – 1 = 0
2x + y – 11 = 0 => y = 11 – 2x
Substituting some different values of x, we get their corresponding values of y as shown below:

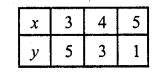
Now plot the points and join them Similarly in x – y – 1= 0 => x = y + 1

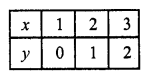
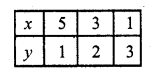
Now plot the points and join them We see that these two lines intersect each othetr at (4, 3) and intersect y-axis at (0, 11) and (0,-1)

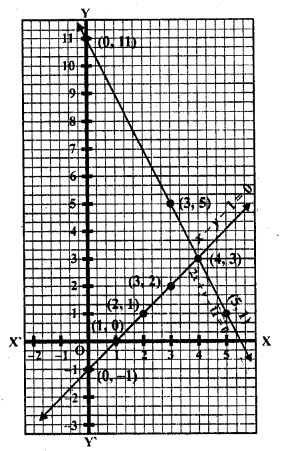
(iv) x + 2y – 7 = 0, 2x – y – 4 = 0
x + 2y – 7 = 0
x = 7 – 2y
Substituting some different value of y, we get their corresponding values of x as shown below

Now plot these points and join then Similarly in
2x – y – 4 = 0
y = 2x – 4

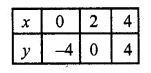
Now plot these points and join them We see that these two lines intersect each other at (3, 2)
and these lines intersect y-axis at (0, \(\frac { 7 }{ 2 }\)) and (0, -4)

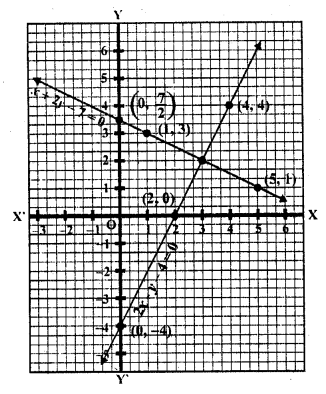
(v) 3x + y – 5 = 0, 2x – y – 5 = 0
3x + y – 5= 0
y = 5 – 3x
Substituting some different values of x, we get corresponding values of y as shown below

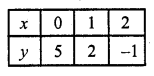
Now plot these points and join them Similarly in 2x – y – 5 = 6 => y = 2x – 5

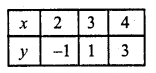
Now plot these points and join them We see that these two lines intersect each other at (2, -1)
x = 2, y = 1
and these Lines intersect y-axis at (0, 5) and (0, -5) respectively.

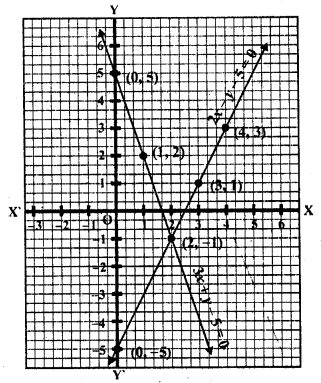
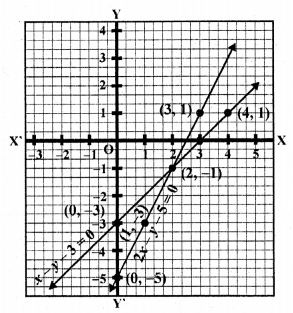
(vi) 2x – y – 5 = 0, x – y – 3 = 0
2x – y – 5 = 0
y = 2x – 5
Substituting some different values of x, we get their corresponding values of y as shown below

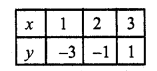
Plot the poinfs and join them Similarly in-the equation x – y – 3 = 0 => x =y + 3

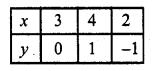
Plot these points on the graph and join them we see that these two lines intersect each other at (2, -1)
x = 2, y = 1
and these lines intersect y-axis at (0, -5) and (0, -3)

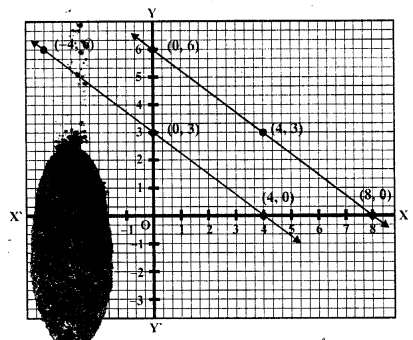
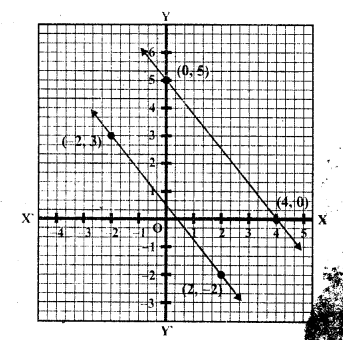
Question 23.
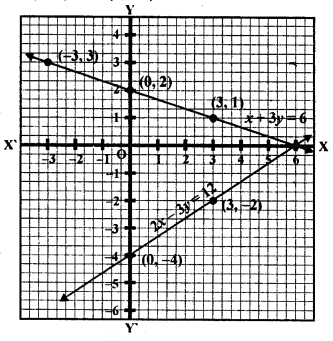
Solve the following system of linear equations graphically and shade the region between the two lines and x-axis
(i) 2x + 3y = 12, x – y = 1 (C.B.S.E. 2001)
(ii) 3x + 2y – 4 = 0, 2x – 3y – 7 = 0 (C.B.S.E. 2006C)
(iii) 3x + 2y – 11 = 0, 2x – 3y + 10 = 0 (C.B.S.E. 2006C)
Solution:
(i) 2x + 3y = 12, x – y = 1
2x + 3y = 12 => 2x = 12 – 3y
=> x = \(\frac { 12 – 3y }{ 2 }\)
Substituting some different values of y, we get corresponding values of x as shown below

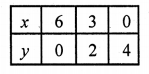
Now plot the points on the graph and join them. Similarly in the equation
x – y = 1 => x = 1 + y

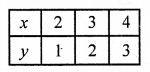
Now plot the points on the graph and join them
We see the two lines intersect each other at (3, 2) and intersect also x-axis at (6, 0) and 0,0)
The required region has been shaded.

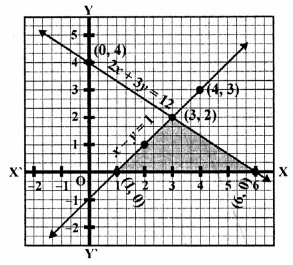
(ii) 3x + 2y – 4 = 0, 2x – 3y – 7 = 0
3x + 2y – 4 = 0
=> 3x = 4 – 2y
x = \(\frac { 4 – 2y }{ 3 }\)
Substituting some different values of y, we get corresponding values of x as shown below

Now plot the points on the graph and join them. Similarly in the equation
2x – 3y – 7 = 0
=> 2x = 3y + 7
=> x = \(\frac { 3y + 7 }{ 2 }\)

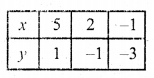
Plot these points and join them
The required region surrounded by these two lines and x-axis has been shaded as shown.

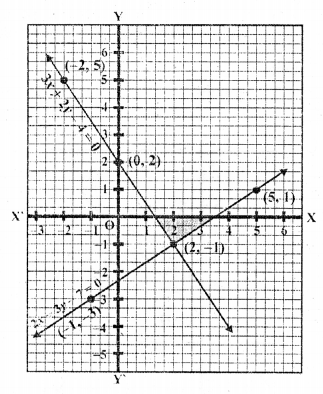
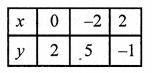
(iii) 3x + 2y – 11 = 0, 2x – 3y + 10 = 0
3x + 2y – 11
=> 3x = 11 – 2y
=> x = \(\frac { 11 – 2y }{ 3 }\)
Substituting some different value of y, we get corresponding values of x as shown below

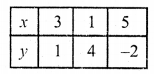
Now plot the points and join them. Similarly in the equation
2x – 3y + 10 = 0
2x = 3y – 10
x = \(\frac { 3y – 10 }{ 2 }\)

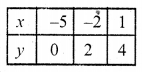
Now plot the points and join them
The required region surrounded by these two lines and Y-axis has been shaded as shown.

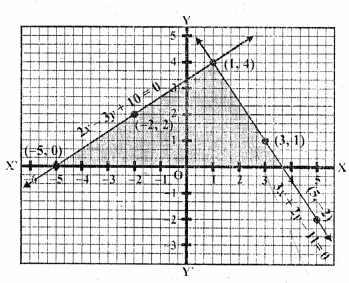
Question 24.
Draw the graphs of the following equations on the same graph paper :
2x + 3y =12
x – y = 1
Find the co-ordinates of the vertices of the triangle formed by the two straight lines and the y-axis. (C.B.S.E. 2001)
Solution:
2x + 3y = 12
⇒ 2x = 12 – 3y
x = \(\frac { 12 – 3y }{ 2 }\)
Substituting some different values of y, we get corresponding values of x as shown below

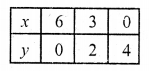
Now plot the points on the graph and join them. Similarly in the equation
x – y = 1 => x = y + 1

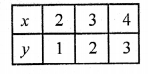
Now plot the points on the graph and join them
The required region surrounded by these two lines and y-axis has been shaded as shown

Question 25.
Draw the graphs of x – y + 1 = 0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and x-axis and shade the triangular area. Calculate the area bounded by these lines and x-axis. (C.B.S.E. 2002)
Solution:
x – y + 1 =0, 3x + 2y-12 = 0
x – y + 1 = 0
x = y – 1
Substituting some different values of y, we get so their corresponding values of x as shown below :

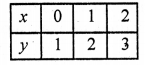
Now plot the points and join them Similarly, in the equation
3x + 2y – 12 = 0 => 3x = 12 – 2y
x = \(\frac { 12 – 2y }{ 3 }\)

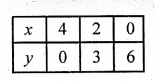
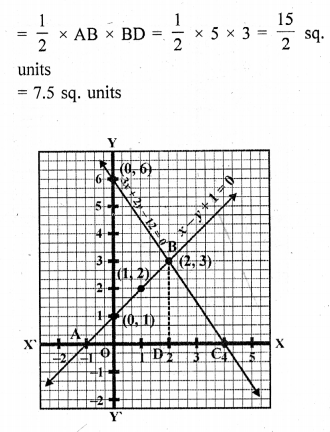
Plot the points on the graph and join them. These two lines intersect each other at (2, 3) and x-axis at (-1, 0) and (4, 0)
Area of the triangle ABC = \(\frac { 1 }{ 2 }\) x Base x Altitude

Question 26.
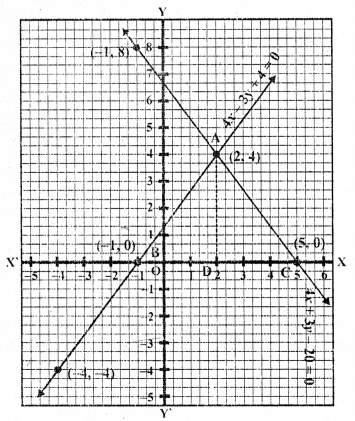
Solve graphically the system of linear equations :
4x – 3y + 4 = 0
4x + 3y – 20 = 0
Find the area bounded by these lines and x-axis. (C.B.S.E. 2002)
Solution:
4x – 3y + 4 = 0
=> 4x = 3y – 4
=> x = \(\frac { 3y – 4 }{ 4 }\)
Substituting some different values of y, we get their corresponding values of x as shown below:

Question 27.
Solve the following system of linear equations graphically 3x + y – 11 = 0, x – y – 1 = 0. Shade the region bounded by these lines and y-axis. Also find the area of the region bounded by the these lines and y-axis. (C.B.S.E. 2002C)
Solution:
3x + y – 11=0
y = 11 – 3x
Substituting some different values of x, we get their corresponding values of y as shown below :

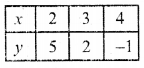
Now plot these points on the graph and join them Similarly in equation
x – y – 1 = 0
=> x = y + 1

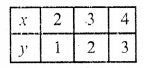
Now plot these points on the graph and join them. We see that these two lines intersect each other at the point (3,2)
x = 3, y = 2
Now shade the region enclosed by these two lines and y-axis

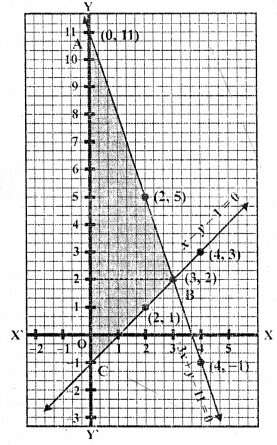
Area of shaded ∆ABC
= \(\frac { 1 }{ 2 }\) x AC x BD
= \(\frac { 1 }{ 2 }\) x 12 x 3 = 18 sq. units

Question 28.
Solve graphically each of the following systems of linear equations. Also find the co-ordinates of the points where the lines meet the axis of x in each system.
(i) 2x + y = 6
x – 2y = -2 (C.B.S.E. 1998)
(ii) 2x – y = 2
4x – y = 8 (C.B.S.E. 1998)
(iii) x + 2y = 5
2x – 3y = -4 (C.B.S.E. 2005)
(iv) 2x + 3y = 8
x – 2y = -3 (C.B.S.E. 2005)
Solution:
(i) 2x + y = 6, x – 2y = -2
2x + y = 6
y = 6 – 2x
Substituting some different values of x, we get their corresponding values of y as shown below

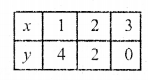
Now plot the points and join them Similarly in the equation
x – 2y = -2
=> x = 2y – 2

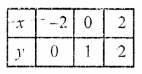
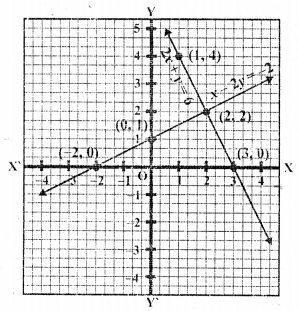
Now plot the points and join them We see that these two lines intersect each other at (2, 2)
x = 2, y = 2
Here two lines also meet x-axis at (3, 0) and (-2, 0) respectively as shown in the figure.

(ii) 2x – y = 2, 4x – y = 8
2x – y = 2
=> y = 2x – 2
Substituting some different values of x, we get corresponding values of y as shown below:

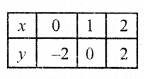
Now plot the points on the graph and join them Similarly in equation
4x – y = 8
=> y = 4x – 8

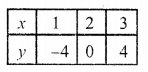
Now plot these points and join them We see that these two lines intersect each other at (3, 4)
x = 3, y = 4
These two lines also meet x-axis at (1, 0) and (2,0) respectively as shown in the figure

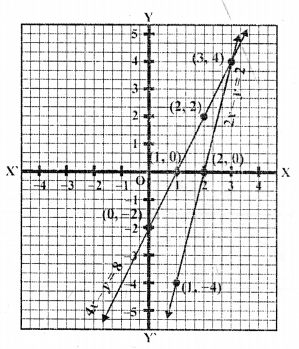
(iii) x + 2y = 5, 2x – 3y = -4
x + 2y = 5
=> x = 5 – 2y
Substituting some different values of y, we get their corresponding values of x as shown below

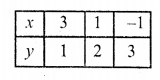
Now plot the points on the graph and join them
Similarly in the equation
2x – 3y = 4
=> 2x = 3y – 4
x = \(\frac { 3y – 4 }{ 2 }\)

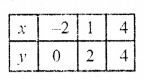
Plot these points and join them
We see that these two lines intersect each other at (1, 2)
x = 1, y = 2
and these two lines meet x-axis at (5, 0) and (-2, 0) respectively as shown in the figure

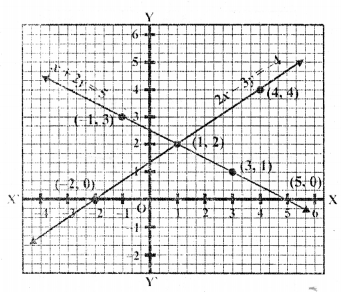
(iv) 2x + 3y = 8, x – 2y = -3
2x + 3y = 8
=> 2x = 8 – 3y
x = \(\frac { 8 – 3y }{ 2 }\)
Substituting some different values of y, we get their corresponding values of x as shown below:

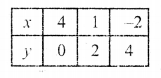
Plot these points on the graph and join them Similarly in equation
x – 2y = -3
x = 2y – 3

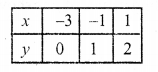
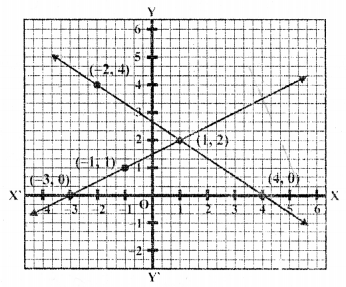
Now plot these points and join them We see that these two lines intersect each other at (1, 2)
x = 1, y = 2
and also these lines meet x-axis at (4, 0) and (-3, 0) respectively as shown in the figure

Question 29.
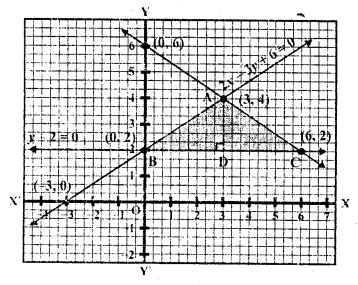
Draw the graphs of the following equations 2x – 3y + 6 = 0
2x + 3y – 18 = 0
y – 2 = 0
Find the vertices of the triangle so obtained. Also, find the area of the triangle.
Solution:
2x – 3y + 6 = 0
2x = 3y – 6
x = \(\frac { 3y – 6 }{ 2 }\)
Substituting some different values of y, we get their corresponding values of x as shown below:

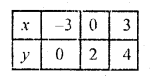
Now plot these points on the graph and join them
Similarly in the equation 2x + 3y -18 = 0
=> 2x = 18 – 3y
x = \(\frac { 18 – 3y }{ 2 }\)

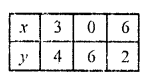
and in equation y – 2 = 0
y = 2
Which is parallel to x-axis on its positive side Now plot the points and join them We see that these lines intersect each other at (3, 4), (6, 2) and (0, 2)
Area of the triangle ABC, so formed
= \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x BC x AD
= \(\frac { 1 }{ 2 }\) x 6 x 2
= 6 sq. units

Question 30.
Solve the following system of equations graphically:
2x – 3y + 6 = 0
2x + 3y – 18 = 0
Also find the area of the region bounded by these two lines and y-axis.
Solution:
2x – 3y + 6 = 0
2x = 3y – 6
x = \(\frac { 3y – 6 }{ 2 }\)
Substituting some different values of y, we get their corresponding values of x as shown below:

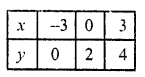
Plot these points on the graph and join them Similarly in the equation
2x + 3y – 18 = 0
=> 2x = 18 – 3y
x = \(\frac { 18 – 3y }{ 2 }\)

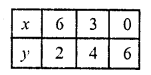
Plot these points on the graph and join them. We see that these two lines intersect each other at (3, 4)
x = 3, y = 4
These lines formed a triangle ABC with the y-axis
Area of ∆ABC = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x BC x AD
= \(\frac { 1 }{ 2 }\) x 4 x 3 = 6 Sq. units

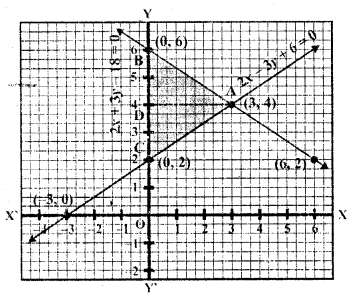
Question 31.
Solve the following system of linear equations graphically :
4x – 5y – 20 = 0
3x + 5y – 15 = 0
Determine the vertices of the triangle formed by the lines representing the above equation and the y-axis. (C.B.S.E. 2004)
Solution:
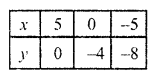
4x – 5y – 20 = 0
=> 4x = 5y + 20
x = \(\frac { 5y + 20 }{ 2 }\)
Substituting some different values of y, we get their corresponding values of x as shown below

Plot these points on the graph and join them Similarly in the equation
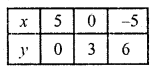
3x + 5y – 15 = 0
=> 3x = 15 – 5y
x = \(\frac { 15 – 5y }{ 2 }\)

Now plot these points and join them We see that these two lines intersect each other at (5, 0)
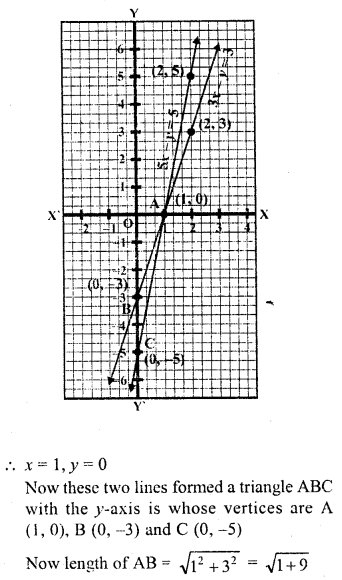
x = 5, y = 0
These two lines form a ∆ABC with y-axis whose vertices are A (5, 0), B (0, 3), C (0, -4)

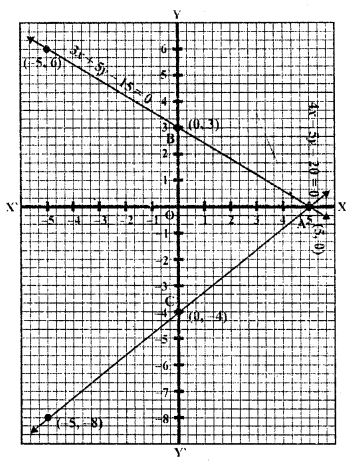
Question 32.
Draw the graphs of the equations 5x – y = 5 and 3x – y = 3. Determine the co-ordinates of the vertices of the triangle formed by these lines and y-axis calculate the area of the triangle so formed.
Solution:
5x – y = 5
=> y = 5x – 5
Substituting some different values of x, we get their corresponding values of y as shown below:

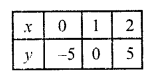
Plot these points on the graph and join them. Similarly in the equation
3x – y = 3
=> y = 3x – 3

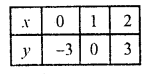
Now plot these points and join them We see that these two lines intersect each other at (1, 0)

Question 33.
Form the pair of linear equations in the following problems, and find their solution graphically.
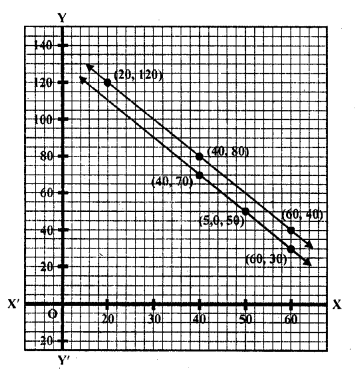
(i) 10 students of class X took part in Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
(ii) 5 pencils and 7 pens together costs Rs. 50, whereas 7 pencils and 5 pens together cost Rs. 46. Find the cost of one pencil and a pen.
(iii) Champa went to a ‘sale’ to purchase some pants and skirts. When her friends asked her how many of each she had bought, she answered, “The number of skirts is two less than twice the number of pants purchased. Also the number of skirts is four less than four times the number of pants purchased.” Help her friends to find how many pants and skirts Champa bought. [NCERT]
Solution:
Let number of boys = x
and number of girls = y
According to the given conditions
x + y = 10
y – x = 4
Now, x + y = 10
=> x = 10 – y
Substituting some different values of y, we get their corresponding values of x as given below

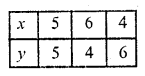
Plot the points on the graph and join them Similarly in the equation
y – x = 4
=> y = 4 + x

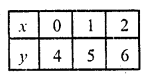
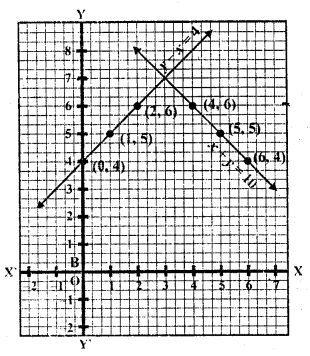
Now plot the points and join them we see that these two lines intersect each other at (3, 7)
x = 3, y = 7
Number of boys = 3
and number of girls = 7

(ii) Let cost of 1 pencil = Rs. x
and cost of 1 pen = Rs. y
According to the given conditions,
5x + 7y = 50
2x + 5y = 46
5x + 7y = 50
5x = 50 – 7y
x = \(\frac { 50 – 7y }{ 5 }\)
Substituting some different values of y, we get them corresponding values of x as given below

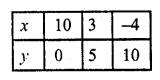
Plot these points and join them Similarly in the equation
7x + 5y = 46
=> 7x = 46 – 5y
=> x = \(\frac { 46 – 5y }{ 7 }\)

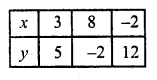
Now plot the points on the graph and join them. We see that these two lines intersect each other at (3, 5)
x = 3, y = 5
or cost of pencil = Rs. 3
and cost of a pen = Rs. 5

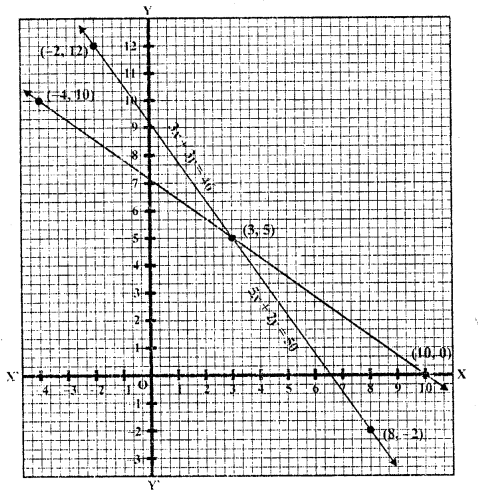
(iii) Let number of skirts = x
and number of pants = y
According to the given condition,
x = 2y – 2 and x = 4y – 4
2y – 2 = 4y – 4
4y – 2y = -2 + 4
2y = 2
y = 1
and x = 2y – 2 = 2 x 1 – 2 = 2 – 2 = 0
Number of skirts = 0
and number of pants = 1

Question 34.
Solve the following system of equations graphically shade the region between the lines and the y -axis
(i) 3x – 4y = 7
5x + 2y = 3 (C.B.S.E. 2006C)
(ii) 4x – y = 4
3x + 2y = 14 (C.B.S.E. 2006C)
Solution:
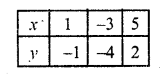
(i) 3x – 4y = 7
3x = 7 + 4y
x = \(\frac { 7 + 4y }{ 3 }\)
Substituting some different values of y, we get their corresponding values of x as shown below

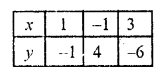
Plot these points on the graph and join them. Similarly in the equation
5x + 2y = 3
=> 5x = 3 – 2y
x = \(\frac { 3 – 2y }{ 5 }\)

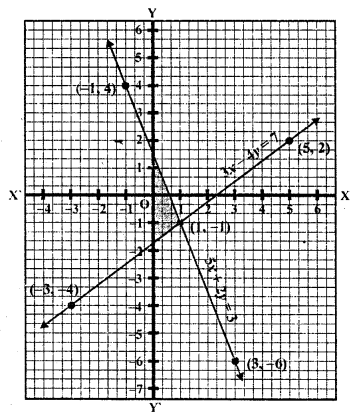
Plot these points and join them We see that the lines intersect each other at (1, -1)
x = 1, y = -1
Now the region between the these lines and y-axis has been shaded as shown

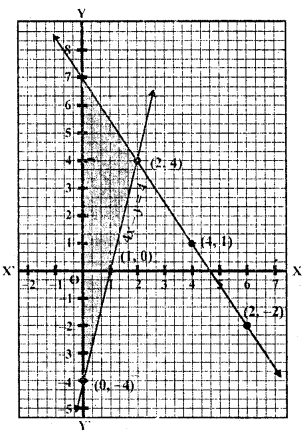
(ii) 4x – y = 4
3x + 2y = 14
4x – y = 4
y = 4x – 4
Substituting some different values of x, we get their corresponding values of y as given below

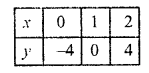
Plot these points and join them Similarly in equation
3x + 2y = 14
3x = 14 – 2y
x = \(\frac { 14 – 2y }{ 3 }\)

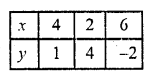
Now plot these points and join them
We see that these lines intersect each other at (2, 4)
x = 2, y = 4
The region between these two lines and y-axis has been shaded as shown

Question 35.
Represent the following pair of equations graphically and write the coordinates of points where the lines intersects y-axis
x + 3y = 6
2x – 3y = 12 (C.B.S.E. 2008)
Solution:
x + 3y = 6
x = 6 – 3y
Substituting some different values of y, we get their corresponding values of x as shown below

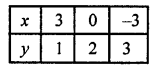
Now plot these points on the graph and join them
Similarly in the equation
2x – 3y = 12 => 2x = 12 + 3y
x = \(\frac { 12 + 3y }{ 2 }\)

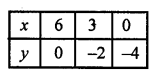
Now plot there points and join them We see that these two lines meet y-axis at (0, 2) and (0, -4)

Question 36.
Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is
(i) intersecting lines
(ii) Parallel lines
(iii) coincident lines [NCERT]
Solution:
Given a linear equation 2x + 3y – 8 = 0
(i) When the lines are intersecting, then

Question 37.
Determine graphically the co-ordinates of the vertices of a triangle, the equations of whose sides are :
(i) y = x, y = 2x and y + x = 6 (C.B.S.E. 2000)
(ii) y = x, 3y = x, x + y = 8 (C.B.S.E. 2000)
Solution:
(i) y = x
Substituting some different values of x, we get their corresponding values of y as shown below

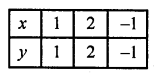
Now plot the points on the graph and join them. Similarly in the equation y = 2x

and y + x = 6 => x = 6 – y

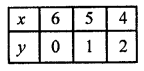
Now plot the points on the graph and join them. We see that these lines intersect each other at (0, 0), (3, 3) and (2, 4)
Vertices of the triangle so formed by these lines are (0, 0), (3, 3) and (2, 4)

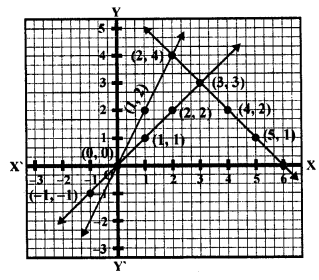
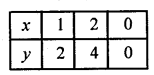
(ii) y = x, 3y = x, x + y = 8
y = x
Substituting some different values of x, we get corresponding values of y as shown below

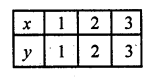
Plot these points on the graph and join them Similarly in the equation 3y = x

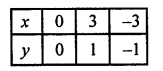
and x + y = 8 => x = 8 – y

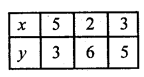
Now plot the points and join them. We see that these lines intersect each other at (0,0), (4, 4), (6, 2)
The vertices of the triangle so formed are (0, 0), (4, 4) and (6, 2)

Question 38.
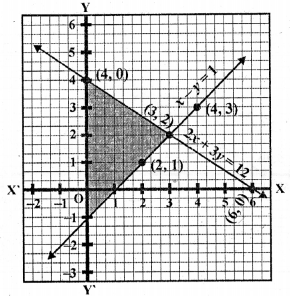
Graphically, solve the following pair of equations:
2x + y = 6
2x – y + 2 = 0
Find the ratio of the areas of the two triangles formed by the lines representing these equations with the x-axis and the lines with the y-axis. [NCERT Exemplar]
Solution:
Given equations are 2x + y – 6 and 2x – y + 2 = 0
Table for equation 2x + y = 6



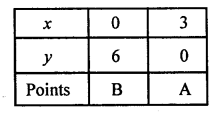
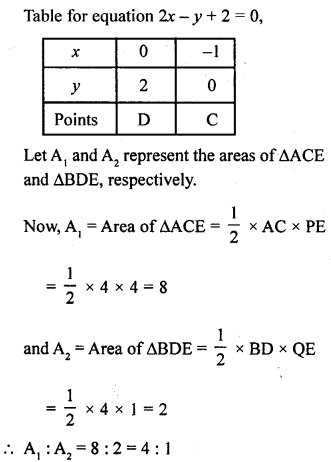
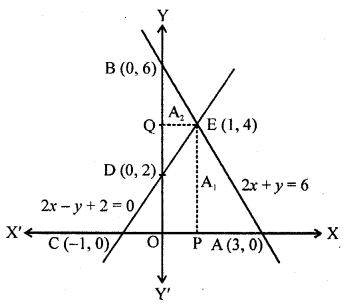
Hence, the pair of equations intersect graphically at point E (1, 4), i.e., x = 1 and y = 4

Question 39.
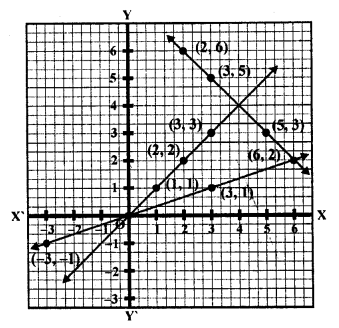
Determine, graphically, the vertices of the triangles formed by the lines y = x, 3y = x, x + y = 8. [NCERT Exemplar]
Solution:
Given linear equations are y = x …….(i)
3y = x ………(ii)
and x + y = 8 …….(iii)
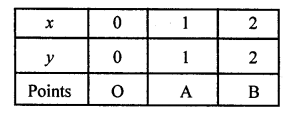
For equation y = x,
If x = 1, then y = 1
If x = 0, then y = 0
If x = 2, then y = 2
Table for line y = x,

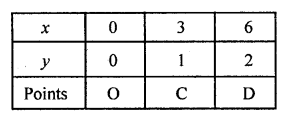
For equation x = 3y
If x = 0, then y = 0,
if x = 3, then y = 1
and if x = 6, then y = 2
Table for line x = 3y,

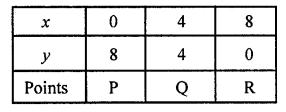
For equation,
If x = 0, then y = 8
if x = 8, then y = 0
and if x = 4, then y = 4
Table for line x + y = 8,

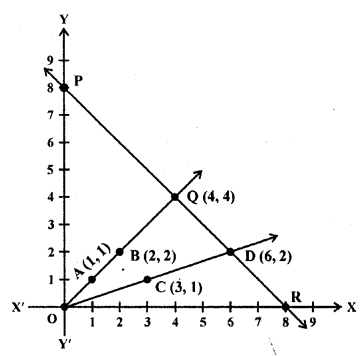
Plotting the points A (1, 1) and B (2,2), we get the straight line AB. Plotting the points C (3, 1) and D (6, 2), we get the straight line CD. Plotting the points P (0, 8), Q (4, 4) and R (8, 0), we get the straight line PQR. We see that lines AB and CD intersecting the line PR on Q and D, respectively.
So, ∆OQD is formed by these lines. Hence, the vertices of the ∆OQD formed by the given lines are O (0, 0), Q (4, 4) and D (6, 2).

Question 40.
Draw the graph of the equations x = 3, x = 5 and 2x – y – 4 = 0. Also, find the area of the quadrilateral formed by the lines and the x-axis. |NCERT Exemplar]
Solution:
Given equation of lines 2x – y – 4 = 0, x = 3 and x = 5
Table for line 2x – y – 4 = 0,

Draw the points P (0, -4) and Q (2,0) and join these points and form a line PQ also draw the lines x = 3 and x = 5.
Area of quadrilateral ABCD = \(\frac { 1 }{ 2 }\) x distance between parallel lines (AB) x (AD + BC) [since, quadrilateral ABCD is a trapezium]
= \(\frac { 1 }{ 2 }\) x 2 x (6 + 2) [∵ AB = OB – OA = 5 – 3 = 2, AD = 2 and BC = 6]
= 8 sq. units

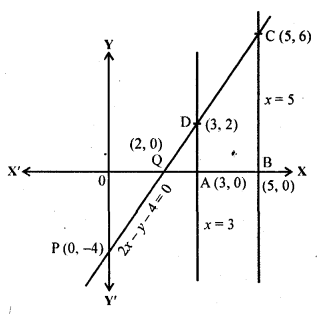
Hence, the required area of the quadrilateral formed by the lines and the x-axis is 8 sq. units.

Question 41.
Draw the graphs of the lines x = -2, and y = 3. Write the vertices of the figure formed by these lines, the x-axis and the y-axis. Also, find the area of the figure. [NCERT Exemplar]
Solution:
We know that the graph of x = -2 is a line parallel to y-axis at a distance of 2 units to the left of it. So, the line l is the graph of x = -2

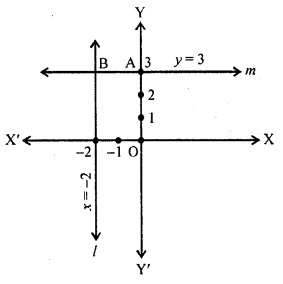
The graph of y = 3 is a line parallel to the x-axis at a distance of 3 units above it.
So, the line m is the graph of y = 3
The figure enclosed by the line x = -2, y = 3, the x-axis and the y-axis is OABC, which is a rectangle.
A is a point on the y-axis at a distance of 3 units above the x-axis. So, the coordinates of A are (0, 3).
C is a point on the x-axis at a distance of 2 units to the left of y-axis. So, the coordinates of C are (-2, 0).
B is the solution of the pair of equations x = -2 and y = 3. So, the coordinates of B are (-2, 3).
So, the vertices of the rectangle OABC are O (0, 0), A (0, 3), B (-2, 3), C (-2, 0).
The length and breadth of this rectangle are 2 units and 3 units, respectively.
As the area of a rectangle = length x breadth, the area of rectangle OABC = 2 x 3 = 6 sq. units.

Question 42.
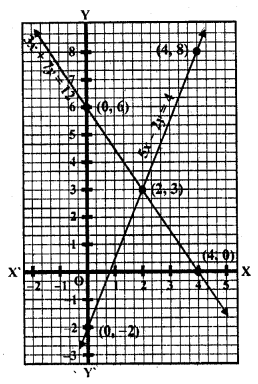
Draw the graphs of the pair of linear equations x – y + 2 = 0 and 4x – y – 4 = 0. Calculate the area of the triangle formed by the lines so drawn and the x-axis. [NCERT Exemplar]
Solution:
For drawing the graphs of the given equations, we find two solutions of each of the equations, which are given in table.
Plot the points A (0,2), B (-2,0), P (0, -4) and Q (1,0) on the graph paper, and join the points to form the lines AB and PQ as shown in the figure.

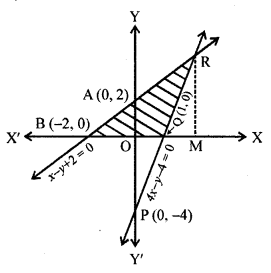
We observe that there is a point R (2,4) common to both the lines AB and PQ. The triangle formed by these lines and the x-axis is BQR.
The vertices of this triangle are B (-2, 0), Q (1, 0) and R (2, 4).
We know that;
Area of triangle = \(\frac { 1 }{ 2 }\) x Base x Altitude
Here, Base = BQ = BO + OQ = 2 + 1 = 3 units
Altitude = RM = Ordinate of R = 4 units.
So, area of ABQR = \(\frac { 1 }{ 2 }\) x 3 x 4 = 6 sq. units

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1
• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2
• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.3
• RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS
• RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS

Answer each of the following questions in one word or one sentence or as per the exact requirement of the questions :
Question 1.
Define a polynomial with real co-efficients.
Solution:

Question 2.
Define degree of a polynomial.
Solution:
The exponent of the highest degree term in a polynomial is known as its degree. A polynomial of degree O is called a constant polynomial.

Question 3.
Write the standard form of a linear polynomial with real co-efficients.
Solution:
ax + b is the standard form of a linear polynomial with real co-efficients and a ≠ 0

Question 4.
Write the standard form of a quadratic polynomial with real co-efficients.
Solution:
ax² + bx + c is a standard form of quadratic polynomial with real co-efficients and a ≠ 0.

Question 5.
Write the standard form of a cubic polynomial with real co-efficients.
Solution:
ax³ + bx² + cx + d is a standard form of cubic polynomial with real co-efficients and a ≠ 0.

Question 6.
Define value of a polynomial at a point.
Solution:
If f(x) is a polynomial and a is any real number then the real number obtained by replacing x by α in f(x) is called the value of f(x) at x = α and is denoted by f(α).

Question 7.
Define zero of a polynomial.
Solution:
A real number a is a zero of a polynomial f(x) if f(α) = 0.

Question 8.
The sum and product of the zeros of a quadratic polynomial are – \(\frac { 1 }{ 2 }\) and -3 respectively. What is the quadratic polynomial ?
Solution:

Question 9.
Write the family of quadratic polynomials having – \(\frac { 1 }{ 4 }\) and 1 as its zeros.
Solution:

Question 10.
If the product of zeros of the quadratic polynomial f(x) = x² – 4x + k is 3, find the value of k.
Solution:
We know that a quadratic polynomial x² – (sum of zeros) x + product of zeros
In the given polynomial f(x) = x² – 4x + k is the product of zeros which is equal to 3
k = 3

Question 11.
If the sum of the zeros of a quadratic polynomial f(x) = kx² – 3x + 5 is 1, write the value of k.
Solution:
f (x) = kx² – 3x + 5
Here a = k, b = -3, c = 5

Question 12.
In the figure, the graph of a polynomial p (x) is given. Find the zeros of the polynomial.

Solution:
The graph of the given polynomial meets the x-axis at -1 and -3
Zero will be -1 and -3
Zero of polynomial is 3

Question 13.
The graph of a polynomial y = f(x) is given below. Find the number of real zeros of f (x).

Solution:
The curve touches x-axis at one point and also intersects at one point So number of zeros will be 3, two equal and one distinct

Question 14.
The graph of the polynomial f(x) = ax² + bx + c is as shown below (in the figure) write the signs of ‘a’ and b² – 4ac.

Solution:
The shape of parabola is up word a > 0
and b² – 4ac >0 i.e., both are positive.

Question 15.
The graph of the polynomial f(x) = ax² + bx + c is as shown in the figure write the value of b² – 4ac and the number of real zeros of f(x).

Solution:
The curve parabola touches the x-axis at one point
It has two equal zeros
b² – 4ac = 0

Question 16.
In Q. No. 14, write the sign of c
Solution:
The mouth of parabola is upward and intersect y-axis above x-axis
c > 0

Question 17.
In Q. No. 15, write the sign of c.
Solution:
The mouth of parabola is downward and intersects y-axis below x-axis
c < 0

Question 18.
The graph of a polynomial f (x) is as shown in the figure. Write the number of real zeros of f (x).

Solution:
The curves touches the x-axis at two distinct point
It has a pair of two equal zeros i.e., it has 4 real zeros

Question 19.
If x = 1, is a zero of the polynomial f(x) = x³ – 2x² + 4x + k, write the value of k.
Solution:

Question 20.
State division algorithm for polynomials.
Solution:
If f(x) is a polynomial and g (x) is a non zero polynomial, there exist two polynomials q (x) and r (x) such that
f(x) = g (x) x q (x) + r (x)
where r (x) = 0 or degree r (x) < degree g (x)
This is called division algorithm

Question 21.
Give an example of polynomials f(x), g (x), q (x) and r (x) satisfying f(x) = g (x) . q (x) + r (x), where degree r (x) = 0.
Solution:
f (x) = x³ + x² + x + 4
g (x) = x + 1
q (x) = x² + 1
r (x) = 3
is an example of f (x) = g (x) x q (x) + r (x)
where degree of r (x) is zero.

Question 22.
Write a quadratic polynomial, sum of whose zeros is 2√3 and their product is 2.
Solution:
Sum of zeros = 2 √3
and product of zeros = 2
Quadratic polynomial will be f (x) = x2 – (sum of zeros) x + product of zeros
= x² – 2 √3 x + 2

Question 23.
If fourth degree polynomial is divided by a quadratic polynomial, write the degree of the remainder.
Solution:
Degree of the given polynomial = 4
and degree of divisor = 2
Degree of quotient will be 4 – 2 = 2
and degree of remainder will be less than 2 In other words equal to or less than one degree

Question 24.
If f(x) = x³ + x² – ax + b is divisible by x² – x, write the value of a and b.
Solution:

Question 25.
If a – b, a and a + b are zeros of the polynomial f(x) = 2x³ – 6x² + 5x – 7, write the value of a.
Solution:

Question 26.
Write the coefficients of the polynomial p (z) = z⁵ – 2z² + 4.
Solution:
p (z) = z⁵ + oz⁴ + oz³ – 2z² + oz + 4
Coefficient of z⁵ = 1
Coefficient of z⁴ = 0
Coefficient of z³ = 0
Coefficient of z² = – 2
Coefficient of z = 0
Constant = 4

Question 27.
Write the zeros of the polynomial x² – x – 6. (C.B.S.E. 2008)
Solution:

Question 28.
If (x + a) is a factor of 2x² + 2ax + 5x + 10, find a. (C.B.S.E. 2008)
Solution:
x + a is a factor of

Question 29.
For what value of k, -4 is a zero of the polynomial x² – x – (2k + 2) ? (CBSE 2009)
Solution:

Question 30.
If 1 is a zero of the polynomial p (x) = ax² – 3 (a – 1) x – 1, then find the value of a.
Solution:

Question 31.
If α, β are the zeros of a polynomial such that α + β = -6 and α β = -4, then write the polynomial. [CBSE 2010]
Solution:

Question 32.
If α, β are the zeros of the polynomial 2y² + 7y + 5, write the value of α + β + αβ. [CBSE 2010]
Solution:

Question 33.
For what value of k, is 3 a zero of the polynomial 2x² + x + k ? [CBSE 2010]
Solution:
3 is a zero of f(x) = 2x² + x + k
It will satisfy the polynomial
f(x) = 0 ⇒ f(3) = 0
Now 2x² + x + k = 0
=> 2 (3)² + 3 + k = 0
=> 18 + 3 + k = 0
=> 21 + k = 0
=> k = -21

Question 34.
For what value of k, is -3 a zero of the polynomial x² + 11x + k ? [CBSE 2010]
Solution:
-3 is a zero of polynomial f(x) = x² + 11x + k
It will satisfy the polynomial
f (x) = 0 => f(-3) = 0
Now x² + 11x + k = 0
=> (-3)²+ 11 x (-3) + k = 0
⇒ 9 – 33 + k = 0
⇒ -24 + k = 0
⇒ k = 24

Question 35.
For what value of k, is -2 a zero of the polynomial 3x² + 4x + 2k ? [CBSE 2010]
Solution:
-2 is a zero of the polynomial
f(x) = 3x² + 4x + 2k
f(-2) = 0
=> 3 (-2)² + 4 (-2) + 2k = 0
=> 12 – 8 + 2k = 0
=> 4 + 2k = 0
=> 2k = -4
=> k = -2

Question 36.
If a quadratic polynomial f(x) is factorizable into linear distinct factors, then what is the total number of real and distinct zeros of f (x) ?
Solution:
In a quadratic polynomial f(x) its degree is 2 and it can be factorised in to two distinct linear factors.
f(x) has two distinct zeros

Question 37.
If a quadratic polynomiaI f(x) is a square of a linear polynomial, then its two zeros are coincident. (True / False)
Solution:
In a quadratic polynomial f(x), it is the square of a linear polynomial It has two zeros which are equal i.e. coincident
It is true

Question 38.
If a quadratic polynomial f(x) is not factorizable into linear factors, then it has no real zero. (True / False)
Solution:
A quadratic polynomial f(x) is not factorised into linear factors It has no real zeros It is true

Question 39.
If f(x) is a polynomial such that f(a) f(b) < 0, then what is the number of zeros lying between a and b ?
Solution:
f(x) is a polynomial such that f(a) f(b) < 0
At least one of its zeros will be between a and b

Question 40.
If graph of quadratic polynomial ax² + bx + c cuts positive direction of y-axis, then what is the sign of c ?
Solution:
The graph of quadratic polynomial ax² + bx + c cuts positive direction of y-axis Then sign of constant term c will be also positive.

Question 41.
If the graph of quadratic polynomial ax² + bx + c cuts negative direction of y-axis, then what is the sigh of c ?
Solution:
The graph of quadratic polynomial ax² + bx + c cuts negative side of y-axis
Then sign of constant term c will be negative

Hope given RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2

Other Exercises

• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1
• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2
• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.3
• RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS
• RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS

Question 1.
Verify that numbers given along side of the cubic polynomials below are their zeros. Also, verify the relationship between the zeros and coefficients in each case :
(i) f(x) = 2x³ – x² – 5x + 2 ; \(\frac { 1 }{ 2 }\) , 1, -2
(ii) g(x) = x³ – 4x² + 5x – 2 ; 2, 1, 1
Solution:

Question 2.
Find a cubic polynomial with the sum, sum of product of its zeros taken two at a time and product of its zeros as 3, -1 and -3 respectively.
Solution:

Question 3.
If the zeros of the polynomial f(x) = 2x³ – 15x² + 37x – 30 are in AP. Find them.
Solution:

Question 4.
Find the condition that the zeros of the polynomial f(x) = x³ + 3px² + 3qx + r may be in AP.
Solution:

Question 5.
If the zeros of the polynomial f(x) = ax³ + 3bx² + 3cx + d are in A.P., prove that 2b³ – 3abc + a²d = 0.
Solution:

Question 6.
If the zeros of the polynomial f(x) = x³ – 12x² + 39x + k are in AP, find the value of k.
Solution:

Hope given RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1
• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.2
• RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.3
• RD Sharma Class 10 Solutions Chapter 2 Polynomials VSAQS
• RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS

Question 1.
Find the zeros of each of the following quadratic polynomials and verify the relationship between the zeros and their co-efficients :

Solution:
(i) f(x) = x² – 2x – 8

Question 2.
For each of the following, find a quadratic polynomial whose sum and product respectively of the zeroes are as given. Also, find the zeroes of these polynomials by factorization.

Solution:
(i) Given that, sum of zeroes (S) = – \(\frac { 8 }{ 3 }\)
and product of zeroes (P) = \(\frac { 4 }{ 3 }\)
Required quadratic expression,

Question 3.
If α and β are the zeros of the quadratic polynomial f(x) = x² – 5x + 4, find the value of \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta } -2\alpha \beta\).
Solution:

Question 4.
If α and β are the zeros of the quadratic polynomial p(y) = 5y² – 7y + 1, find the value of \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta }\)
Solution:

Question 5.
If α and β are the zeros of the quadratic polynomial f(x) = x² – x – 4, find the value of \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta } -\alpha \beta\)
Solution:

Question 6.
If α and β are the zeros of the quadratic polynomial f(x) = x² + x – 2, find the value of \(\frac { 1 }{ \alpha } -\frac { 1 }{ \beta }\)
Solution:

Question 7.
If one zero of the quadratic polynomial f(x) = 4x² – 8kx – 9 is negative of the other, find the value of k.
Solution:

Question 8.
If the sum of the zeros of the quadratic polynomial f(t) = kt² + 2t + 3k is equal to their product, find the value of k.
Solution:

Question 9.
If α and β are the zeros of the quadratic polynomial p(x) = 4x² – 5x – 1, find the value of α²β + αβ².
Solution:

Question 10.
If α and β are the zeros of the quadratic polynomial f(t) = t² – 4t + 3, find the value of α⁴β³ + α³β⁴.
Solution:

Question 11.
If α and β are the zeros of the quadratic polynomial f (x) = 6x⁴ + x – 2, find the value of \(\frac { \alpha }{ \beta } +\frac { \beta }{ \alpha }\)
Solution:

Question 12.
If α and β are the zeros of the quadratic polynomial p(s) = 3s² – 6s + 4, find the value of \(\frac { \alpha }{ \beta } +\frac { \beta }{ \alpha } +2\left( \frac { 1 }{ \alpha } +\frac { 1 }{ \beta } \right) +3\alpha \beta\)
Solution:

Question 13.
If the squared difference of the zeros of the quadratic polynomial f(x) = x² + px + 45 is equal to 144, find the value of p
Solution:

Question 14.
If α and β are the zeros of the quadratic polynomial f(x) = x² – px + q, prove that:

Solution:

Question 15.
If α and β are the zeros of the quadratic polynomial f(x) = x² – p(x + 1) – c, show that (α + 1) (β + 1) = 1 – c.
Solution:

Question 16.
If α and β are the zeros of the quadratic polynomial such that α + β = 24 and α – β = 8, find a quadratic polynomial having α and β as its zeros.
Solution:

Question 17.
If α and β are the zeros of the quadratic polynomial f(x) = x² – 1, find a quadratic polynomial whose zeros are \(\frac { 2\alpha }{ \beta }\) and \(\frac { 2\beta }{ \alpha }\)
Solution:

Question 18.
If α and β are the zeros of the quadratic polynomial f(x) = x² – 3x – 2, find a quadratic polynomial whose zeros are \(\frac { 1 }{ 2\alpha +\beta }\) and \(\frac { 1 }{ 2\beta +\alpha }\)
Solution:

Question 19.
If α and β are the zeroes of the polynomial f(x) = x² + px + q, form a polynomial whose zeros are (α + β)² and (α – β)².
Solution:

Question 20.
If α and β are the zeros of the quadratic polynomial f(x) = x² – 2x + 3, find a polynomial whose roots are :
(i) α + 2, β + 2
(ii) \(\frac { \alpha -1 }{ \alpha +1 } ,\frac { \beta -1 }{ \beta +1 }\)
Solution:

Question 21.
If α and β are the zeros of the quadratic polynomial f(x) = ax² + bx + c, then evaluate :


Solution:

 

Hope given RD Sharma Class 10 Solutions Chapter 2 Polynomials Ex 2.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.1
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.2
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.3
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.6
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers VSAQS
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS

Question 1.
The exponent of 2 in the prime factorisation of 144, is
(a) 4
(b) 5
(c) 6
(d) 3
Solution:
(a)

Question 2.
The LCM of two numbersls 1200. Which of the following cannot be their HCF ?
(a) 600
(b) 500
(c) 400
(d) 200
Solution:
(b) LCM of two number = 1200
Their HCF of these two numbers will be the factor of 1200
500 cannot be its HCF

Question 3.
If n = 2³ x 3⁴ x 4⁴ x 7, then the number of consecutive zeroes in n, where n is a natural number, is
(a) 2
(b) 3
(c) 4
(d) 7
Solution:
(c) Because it has four factors n = 2³ x 3⁴ x 4⁴ x 7
It has 4 zeroes

Question 4.
The sum of the exponents of the prime factors in the prime factorisation of 196, is
(a) 1
(b) 2
(c) 4
(d) 6
Solution:
(c)

Question 5.
The number of decimal places after which the decimal expansion of the rational number \(\frac { 23 }{ { 2 }^{ 2 }\times 5 }\) will terminate, is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b)

Question 6.

(a) an even number
(b) an odd number
(c) an odd prime number
(d) a prime number
Solution:
(a)

Question 7.
If two positive integers a and b are expressible in the form a = pq² and b = p²q ; p, q being prime numbers, then LCM (a, b) is
(a) pq
(b) p³q³
(c) p³q²
(d) p²q²
Solution:
(c) a and b are two positive integers and a =pq² and b = p³q, where p and q are prime numbers, then LCM=p³q²

Question 8.
In Q. No. 7, HCF (a, b) is
(a) pq
(b) p³q³
(c) p³q²
(d) p²q²
Solution:
(a) a = pq² and b =p³q where a and b are positive integers and p, q are prime numbers, then HCF =pq

Question 9.
If two positive integers tn and n arc expressible in the form m = pq³ and n = p³q², where p, q are prime numbers, then HCF (m, n) =
(a) pq
(b) pq²
(c) p³q³
(d) p²q³
Solution:
(b) m and n are two positive integers and m = pq³ and n = pq², where p and q are prime numbers, then HCF = pq²

Question 10.
If the LCM of a and 18 is 36 and the HCF of a and 18 is 2, then a =
(a) 2
(b) 3
(c) 4
(d) 1
Solution:
(c) LCM of a and 18 = 36
and HCF of a and 18 = 2
Product of LCM and HCF = product of numbers
36 x 2 = a x 18
a = \(\frac { 36\times 2 }{ 18 }\) = 4

Question 11.
The HCF of 95 and 152, is
(a) 57
(b) 1
(c) 19
(d) 38
Solution:
(c) HCF of 95 and 152 = 19

Question 12.
If HCF (26, 169) = 13, then LCM (26, 169) =
(a) 26
(b) 52
(f) 338
(d) 13
Solution:
(c) HCF (26, 169) = 13
LCM (26, 169) = \(\frac { 26\times 169 }{ 13 }\) = 338

Question 13.

(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b)

Question 14.
The decimal expansion of the rational \(\frac { 14587 }{ 1250 }\) number will terminate after
(a) one decimal place
(b) two decimal place
(c) three decimal place
(d) four decimal place
Solution:
(d)

Question 15.
If p and q are co-prime numbers, then p² and q² are
(a) co prime
(b) not co prime
(c) even
(d) odd
Solution:
(a) p and q are co-prime, then
p² and q² will also be coprime

Question 16.
Which of the following rational numbers have terminating decimal ?

(a) (i) and (ii)
(b) (ii) and (iii)
(c) (i) and (iii)
(d) (i) and (iv)
Solution:
(d) We know that a rational number has terminating decimal if the prime factors of its denominator are in the form 2^m x 5ⁿ
\(\frac { 16 }{ 225 }\) and \(\frac { 7 }{ 250 }\) has terminating decimals

Question 17.
If 3 is the least prime factor of number a and 7 is the least prime factor of number b, then the least prime factor of a + b, is
(a) 2
(b) 3
(c) 5
(d) 10
Solution:
(a) 3 is the least prime factor of a
7 is the least prime factor of b, then
Sum of a a and b will be divisible by 2
2 is the least prime factor of a + b

Question 18.
\(3.\bar { 27 }\) is
(a) an integer
(b) a rational number
(c) a natural number
(d) an irrational number
Solution:
(b) \(3.\bar { 27 }\) is a rational number

Question 19.
The smallest number by which √27 should be multiplied so as to get a rational number is
(a) √27
(b) 3√3
(c) √3
(d) 3
Solution:
(c)

Question 20.
The smallest rational number by which \(\frac { 1 }{ 3 }\) should be multiplied so that its decimal expansion terminates after one place of decimal, is
(a) \(\frac { 3 }{ 10 }\)
(b) \(\frac { 1 }{ 10 }\)
(c) 3
(d) \(\frac { 3 }{ 100 }\)
Solution:
(a) The smallest rational number which should be multiplied by \(\frac { 1 }{ 3 }\) to get a terminating

Question 21.
If n is a natural number, then 9²ⁿ – 4²ⁿ is always divisible by
(a) 5
(b) 13
(c) both 5 and 13
(d) None of these
Solution:
(c)

Question 22.
If n is any natural number, then 6ⁿ – 5ⁿ always ends with
(a) 1
(b) 3
(c) 5
(d) 7
Solution:
(a) n is any natural number and 6ⁿ – 5ⁿ
We know that 6ⁿ ends with 6 and 5ⁿ ends with 5
6ⁿ – 5ⁿ will end with 6 – 5 = 1

Question 23.
The LCM and HCF of two rational numbers are equal, then the numbers must be
(a) prime
(b) co-prime
(c) composite
(d) equal
Solution:
(d) LCM and HCF of two rational numbers are equal Then those must be equal

Question 24.
If the sum of LCM and HCF of two numbers is 1260 and their LCM is 900 more than their HCF, then the product of two numbers is
(a) 203400
(b) 194400
(c) 198400
(d) 205400
Solution:
(b) Sum of LCM and HCF of two numbers = 1260
LCM = 900 more than HCF
LCM = 900 +HCF
But LCM = HCF = 1260
900 + HCF + HCF = 1260
=> 2HCF = 1260 – 900 = 360
=> HCF = 180
and LCM = 1260 – 180 = 1080
Product = LCM x HCF = 1080 x 180 = 194400
Product of numbers = 194400

Question 25.
The remainder when the square of any prime number greater than 3 is divided by 6, is
(a) 1
(b) 3
(c) 2
(d) 4
Solution:
(a)

Question 26.
For some integer m, every even integer is of the form
(a) m
(b) m + 1
(c) 2m
(d) 2m + 1
Solution:
(c) We know that, even integers are 2, 4, 6, …
So, it can be written in the form of 2m Where, m = Integer = Z
[Since, integer is represented by Z]
or m = …, -1, 0, 1, 2, 3, …
2m = …, -2, 0, 2, 4, 6, …
Alternate Method
Let ‘a’ be a positive integer.
On dividing ‘a’ by 2, let m be the quotient and r be the remainder.
Then, by Euclid’s division algorithm, we have
a – 2m + r, where a ≤ r < 2 i.e., r = 0 and r = 1
=> a = 2 m or a = 2m + 1
When, a = 2m for some integer m, then clearly a is even.

Question 27.
For some integer q, every odd integer is of the form
(a) q
(b) q + 1
(c) 2q
(d) 2q + 1
Solution:
(d) We know that, odd integers are 1, 3, 5,…
So, it can be written in the form of 2q + 1 Where, q = integer = Z
or q = …, -1, 0, 1, 2, 3, …
2q + 1 = …, -3, -1, 1, 3, 5, …
Alternate Method
Let ‘a’ be given positive integer.
On dividing ‘a’ by 2, let q be the quotient and r be the remainder.
Then, by Euclid’s division algorithm, we have
a = 2q + r, where 0 ≤ r < 2
=> a = 2q + r, where r = 0 or r = 1
=> a = 2q or 2q + 1
When a = 2q + 1 for some integer q, then clearly a is odd.

Question 28.
n² – 1 is divisible by 8, if n is
(a) an integer
(b) a natural number
(c) an odd integer
(d) an even integer
Solution:
(c)


At k = -1, a = 4(-1)(-1 + 1) = 0 which is divisible by 8.
At k = 0, a = 4(0)(0 + 1) = 4 which is divisible by 8.
At k = 1, a = 4(1)(1 + 1) = 8 which is divisible by 8.
Hence, we can conclude from above two cases, if n is odd, then n² – 1 is divisible by 8.

Question 29.
The decimal expansion of the rational number \(\frac { 33 }{ { 2 }^{ 2 }\times 5 }\) will terminate after
(a) one decimal place
(b) two decimal places .
(c) three decimal places
(d) more than 3 decimal places
Solution:
(b)

Question 30.
If two positive integers a and b are written as a = x³y² and b = xy³ ; x, y are prime numbers, then HCF (a, b) is
(a) xy
(b) xy²
(c) x³y³
(d) x²y²
Solution:
(b)

[Since, HCF is the product of the smallest power of each common prime factor involved in the numbers]

Question 31.
The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is
(a) 10
(b) 100
(c) 504
(d) 2520
Solution:
(d) Factors of 1 to 10 numbers
1 = 1
2 = 1 x 2
3 = 1 x 3
4 = 1 x 2 x 2
5 = 1 x 5
6 = 1 x 2 x 3
7 = 1 x 7
8 = 1 x 2 x 2 x 2
9 = 1 x 3 x 3
10 = 1 x 2 x 5
LCM of number 1 to 10 = LCM (1, 2, 3, 4, 5, 6, 7, 8, 9, 10)
= 1 x 2 x 2 x 2 x 3 x 3 x 5 x 7 = 2520

Question 32.
The largest number which divides 70 and 125, leaving remainders 5 and 8, respectively, is
(a) 13
(b) 65
(c) 875
(d) 1750
Solution:
(a) Since, 5 and 8 are the remainders of 70 and 125, respectively. Thus, after subtracting these remainders from the numbers, we have the numbers 65 = (70 – 5), 117 = (125 – 8), which is divisible by the required number.
Now, required number = HCF of 65, 117
[For the largest number]
For this, 117 = 65 x 1 + 52 [Dividend = divisor x quotient + remainder]
=> 65 = 52 x 1 + 13
=> 52 = 13 x 4 + 0
HCF = 13
Hence, 13 is the largest number which divides 70 and 125, leaving remainders 5 and 8.

Question 33.
If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of m is
(a) 4
(b) 2
(c) 1
(d) 3
Solution:
(b) By Euclid’s division algorithm,
b = aq + r, 0 ≤ r < a [dividend = divisor x quotient + remainder]
=> 117 = 65 x 1 + 52
=> 65 = 52 x 1 + 13
=> 52 = 13 x 4 + 0
HCF (65, 117)= 13 …(i)
Also, given that HCF (65, 117) = 65m – 117 …..(ii)
From equations (i) and (ii),
65m – 117 = 13
=> 65m = 130
=> m = 2

Question 34.
The decimal expansion of the rational number \(\frac { 14587 }{ 1250 }\) will terminate after:
(a) one decimal place
(b) two decimal places
(c) three decimal places
(d) four decimal places
Solution:
(d)

Hence, given rational number will terminate after four decimal places.

Question 35.
Euclid’s division lemma states that for two positive integers a and b, there exist unique integers q and r such that a = bq + r, where r must satisfy
(a) 1 < r < b
(b) 0 < r ≤ b
(c) 0 ≤ r < b
(d) 0 < r < b
Solution:
(c) According to Euclid’s Division lemma, for a positive pair of integers there exists unique integers q and r, such that
a = bq + r, where 0 ≤ r < b

Hope given RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQSare helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

You can also download MCQ Questions For Class 10 Maths With Answers to help you to revise complete syllabus and score more marks in your examinations.

RD Sharma Class 10 Solutions Chapter 1 Real Numbers VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 1 Real Numbers VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.1
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.2
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.3
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.6
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers VSAQS
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS

Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
Question 1.
State Euclid’s division lemma.
Solution:
Euclid’s division lemma:
Let a and b be any two positive integers, then there exist unique integers q and r such that
a = bq + r, 0 ≤ r < b
If b\a, then r = 0, otherwise x. satisfies the stronger inequality 0 < r < b.

Question 2.
State Fundamental Theorem of Arithmetic.
Solution:
Fundamental Theorem of Arithmetics :
Every composite number can be expressed (factorised) as a product of primes and this factorization is unique except for the order in which the prime factors occur.

Question 3.
Write 98 as product of its prime factors.
Solution:

Question 4.
Write the exponent of 2 in the prime factorization of 144.
Solution:

Question 5.
Write the sum of the exponents of prime factors in the prime factorization of 98
Solution:
98 = 2 x 7 x 7 = 2¹ x 7²
Sum of exponents = 1 + 2 = 3

Question 6.
If the prime factorization of a natural number n is 2³ x 3² x 5² x 7, write the number of consecutive zeros in n.
Solution:
n = 2³ x 3² x 5² x 7
Number of zeros will be 5² x 2² = 10² two zeros

Question 7.
If the product of two numbers is 1080 and their H.C.F. is 30, find their L.C.M.
Solution:
Product of two numbers = 1080
H.C.F. = 30

Question 8.
Write the condition to be satisfied by q so that a rational number \(\frac { p }{ q }\) has a terminating decimal expansion. [C.B.S.E. 2008]
Solution:
In the rational number \(\frac { p }{ q }\) , the factorization of denominator q must be in form of 2^m x 5ⁿ where m and n are non-negative integers.

Question 9.
Write the condition to be satisfied by q so that a rational number \(\frac { p }{ q }\) has a non-terminating decimal expansion.
Solution:
In the rational number \(\frac { p }{ q }\) , the factorization of denominator q, is not in the form of 2^m x 5ⁿ where m and n are non-negative integers.

Question 10.
Complete the missing entries in the following factor tree.

Solution:

Question 11.
The decimal expression of the rational number \(\frac { 43 }{ { 2 }^{ 4 }\times { 5 }^{ 3 } }\) will terminate after how many places of decimals. [C.B.S.E. 2009]
Solution:
The denominator of \(\frac { 43 }{ { 2 }^{ 4 }\times { 5 }^{ 3 } }\) is 24 x 53 which is in the form of 2^m x 5ⁿ where m and n are positive integers
\(\frac { 43 }{ { 2 }^{ 4 }\times { 5 }^{ 3 } }\) has terminating decimals
The decimal expansion of \(\frac { 43 }{ { 2 }^{ 4 }\times { 5 }^{ 3 } }\) terminates after 4 (the highest power is 4) decimal places

Question 12.
Has the rational number \(\frac { 441 }{ { 2 }^{ 5 }\times { 5 }^{ 7 }\times { 7 }^{ 2 } }\) of a terminating or a non terminating decimal representation ? [CBSE 2010]
Solution:

Question 13.
Write whether \(\frac { 2\surd 45+3\surd 20 }{ 2\surd 5 }\) on simplification gives a rational or an irrational number. [CBSE 2010]
Solution:

Question 14.
What is an algorithm ?
Solution:
Algorithm : An algorithm is a series of well defined slips which gives a procedure for solving a type of problem.

Question 15.
What is a lemma ?
Solution:
A lemma is a proven statement used for proving another statement.

Question 16.
If p and q are two prime numbers, then what is their HCF ?
Solution:
If p and q are two primes, then their HCF will be 1 as they have no common factor except 1.

Question 17.
If p and q are two prime numbers, then what is their LCM ?
Solution:
If p and q are two primes, their LCM will be their product.

Question 18.
What is the total number of factors of a prime number ?
Solution:
Total number of factors of a prime number are 2, first 1 and second the number itself.

Question 19.
What is a composite number ?
Solution:
A composite number is a number which can be factorised into more than two factors.

Question 20.
What is the HCF of the smallest composite number and the smallest prime number ?
Solution:
We know that 2 is the smallest prime number and 4 is the smallest composite number
HCF of 2 and 4 = 2

Question 21.
HCF of two numbers is always a factor of their LCM (True / False).
Solution:
True.

Question 22.
π is an irrational number (True / False).
Solution:
True as value of π is neither terminating nor repeating.

Question 23.
The sum of two prime numbers is always a prime number (True / False).
Solution:
False. Sum of two prime numbers can be a composite number
e.g. 3 and 5 are prime numbers but their sum 3 + 5 = 8 is a composite number.

Question 24.
The product of any three consecutive natural numbers is divisible by 6 (True / False).
Solution:
True.

Question 25.
Every even integer is of the form 2m, where m is an integer (True / False).
Solution:
True, as 2m is divisible by 2.

Question 26.
Every odd integer is of the form 2m – 1, where m is an integer (True / False).
Solution:
True, as 2m is an even number but if we subtract 1 from it, it will be odd number.

Question 27.
The product of two irrational numbers is an irrational number (True / False).
Solution:
False, as it is not always possible that the product of two irrational number be also an irrational number, it may be a rational number
for example
√3 x √3 = 3, √7 x √7 = 7

Question 28.
The sum of two irrational numbers is an irrational number (True / False).
Solution:
False, as it is not always possible that the sum of two irrational is also an irrational number, it may be rational number also.
For example
(2 + √3) + (2 – √3) = 2 + √3 + 2 – √3 = 4

Question 29.
For what value of n, 2ⁿ x 5ⁿ ends in 5.
Solution:
In 2ⁿ x 5ⁿ ,
There is no such value of n, which satisifies the given condition.

Question 30.
If a and b are relatively prime numbers, then what is their HCF ?
Solution:
a and b are two prime numbers
Their HCF =1

Question 31.
If a and b are relatively prime numbers, then what is their LCM ?
Solution:
a and b are two prime numbers
Their LCM = a x b

Question 32.
Two numbers have 12 as their HCF and 350 as their LCM (True / False).
Solution:
HCF of two numbers = 12
and LCM is 350
False, as the HCF of two numbers is a factor of their LCM and 12 is not a factor of 350

Hope given RD Sharma Class 10 Solutions Chapter 1 Real Numbers VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two
Variables Ex 3.1

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Question 1.
Akhila went to a fair in her village. She wanted to enjoy rides on the Giant Wheel and play Hoopla (a game in which you throw a rig on the items kept in the stall, and if the ring covers any object completely you get it). The number of times she played Hoopla is half the number of rides she had on the Giant Wheel. Each ride costs Rs. 3, and a game of Hoopla costs Rs. 4. If she spend Rs. 20 in the fair, represent this situation algebraically and graphically.
Solution:
Let number of rides on the wheel = x
and number of play of Hoopla = y
According to the given conditions x = 2y ⇒ x – 2y = 0 ….(i)
and cost of ride on wheel at the rate of Rs. 3 = 3x
and cost on Hoopla = 4y
and total cost = Rs. 20
3x + 4y = 20 ….(ii)
Now we shall solve these linear equations graphically as under
We take three points of each line and join them to get a line in each case the point of intersection will be the solution
From equation (i)
x = 2y

X	4	0	6
y	2	0	3

y = 2, then x = 2 x 2 = 4
y = 0, then x = 2 x 0 = 0
y = 3, then x = 2 x 3 = 6
Now, we plot these points on the graphs and join them to get a line
Similarly in equation (ii)
3x + 4y = 20 ⇒ 3x = 20 – 4y

Now we plot these points and get another line by joining them
These two lines intersect eachother at the point (4, 2)
Its solution is (4, 2)
Which is a unique Hence x = 4, y = 2

Question 2.
Aftab tells his daughter, “Seven years ago, I w as seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be.” Is not this interesting ? Represent this situation algebraically and graphically.
Solution:
Seven years ago
Let age of Aftab’s daughter = x years
and age of Aftab = y years
and 3 years later
Age of daughter = x + 10 years
and age of Aftab = y + 10 years
According to the conditions,
y = 7x ⇒ 7x – y = 0 ……….(i)
y + 10 = 3 (x + 10)
=> y + 10 = 3x + 30
3x – y = 10 – 30 = -20
3x – y = -20 ….(ii)
Equations are
7x – y = 0
3 x – y = -20
Now we shall solve these linear equations graphically as under
7x – y = 0 ⇒ y = 7x

X	0	1	-1
y	0	7	-7

If x = 0, y = 7 x 0 = 0
If x = 1, y = 7 x 1=7
If x = -1, y = 7 x (-1) = -7
Now plot these points on the graph and join
then
3x – y = -20
y = 3x + 20

X	-1	-2	-3
y	17	14	11

If x = -1, y = 3 x (-1) + 20 = -3 + 20= 17
If x = -2, y = 3 (-2) + 20 = -6 + 20 = 14
If x = -3, y = 3 (-3) + 20 = -9 + 20= 11
Now plot the points on the graph and join them we see that lines well meet at a point on producing at (5, 35).

Question 3.
The path of a train A is given by the equation 3x + 4y – 12 = 0 and the path of another train B is given by the equation 6x + 8y – 48 = 0. Represent this situation graphically.
Solution:
Path of A train is 3x + 4y – 12 = 0
and path of B train is 6x + 8y – 48 = 0
Graphically, we shall represent these on the graph as given under 3x + 4y- 12 = 0

Question 4.
Gloria is walking along the path joining (-2, 3) and (2, -2), while Suresh is walking along the path joining (0, 5) and (4, 0). Represent this situation graphically.
Solution:
Plot the points (-2, 3) and (2, -2) and join them to get a line
and also plot the points (0, 5), (4, 0) and joint them to get another line as shown on the graph
We see that these two lines are parallel to each other

Question 5.
On comparing the ratios , and without drawing them, find out whether the lines representing following pairs of linear equations intersect at a point, are parallel or coincide :
(i) 5x – 4y + 8 = 0
7x + 6y – 9 = 0
(ii) 9x + 3y +12 = 0
18x + 6y + 24 = 0
(iii) 6x – 3y +10 = 0
2x – y + 9 = 0
Solution:

Question 6.
Given the linear equation 2x + 3y – 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is :
(i) intersecting lines
(ii) parallel lines
(iii) coincident lines.
Solution:

Question 7.
The cost of 2kg of apples and 1 kg of grapes on a day was found to be Rs. 160. After a month, the cost of 4kg of apples and 2kg of grapes is Rs. 300. Represent the situation algebraically and geo-metrically.
Solution:
Let cost of 1kg of apples = Rs. x
and cost of 1kg of grapes = Rs. y
Now according to the condition, the system of equation will be
2x + y = 160
4x + 2y = 300
Now 2x + y = 160
y = 160 – 2x

X	20	40	60
y	120	80	40

If x = 20, then y = 160 – 2 x 20 = 160 – 40 = 120
If x = 40, then y = 160 – 2 x 40 = 160 – 80 = 80
If x = 60, then y = 160 – 2 x 60 = 160 – 120 = 40
Now plot the points and join them and 4x + 2y = 300
=> 2x + y = 150
=> y = 150 – 2x

X	40	50	60
y	70	50	30

If x = 40, then y = 150 – 2 x 40 = 150 – 80 = 70
If x = 50, then y = 150 – 2 x 50 = 150 – 100 = 50
If x = 60, then y = 150 – 2 x 60 = 150 – 120 = 30
Now plot the points and join them We see that these two lines are parallel

 

Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Mark the correct alternative in each of the following :
Question 1.
If α, β are the zeros of the polynomial f(x) = x² + x + 1, then \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta }\) =
(a) 1
(b) -1
(c) 0
(d) None of these
Solution:
(b)

Question 2.
If α, β are the zeros of the polynomial p(x) = 4x² + 3x + 7, then \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta }\) is equal to
(a) \(\frac { 7 }{ 3 }\)
(b) – \(\frac { 7 }{ 3 }\)
(c) \(\frac { 3 }{ 7 }\)
(d) – \(\frac { 3 }{ 7 }\)
Solution:
(d)

Question 3.
If one zero of the polynomial f(x) = (k² + 4) x² + 13x + 4k is reciprocal of the other, then k =
(a) 2
(b) -2
(c) 1
(d) -1
Solution:
(a) f (x) = (k² + 4) x² + 13x + 4k
Here a = k² + 4, b = 13, c = 4k
One zero is reciprocal of the other
Let first zero = α

k = 2

Question 4.
If the sum of the zeros of the polynomial f(x) = 2x³ – 3kx² + 4x – 5 is 6, then value of k is
(a) 2
(b) 4
(c) -2
(d) -4
Solution:
(b)

Question 5.
If α and β are the zeros of the polynomial f(x) = x² + px + q, then a polynomial having α and β is its zeros is
(a) x² + qx + p
(b) x² – px + q
(c) qx² + px + 1
(d) px² + qx + 1
Solution:
(c)

Question 6.
If α, β are the zeros of polynomial f(x) = x² – p (x + 1) – c, then (α + 1) (β + 1) =
(a) c – 1
(b) 1 – c
(c) c
(d) 1 + c
Solution:
(b)

Question 7.
If α, β are the zeros of the polynomial f(x) = x² – p(x + 1) – c such that (α + 1) (β + 1) = 0, then c =
(a) 1
(b) 0
(c) -1
(d) 2
Solution:
(a)

Question 8.
If f(x) = ax² + bx + c has no real zeros and a + b + c < 0, then
(a) c = 0
(b) c > 0
(c) c < 0
(d) None of these
Solution:
(d) f(x) = ax² + bx + c
Zeros are not real
b² – 4ac < 0 ….(i)
but a + b + c < 0
b < – (a + c)
Squaring both sides b² < (a + c)²
=> (a + c)² – 4ac < 0 {From (i)}
=> (a – c)² < 0
=> a – c < 0
=> a < c

Question 9.
If the diagram in figure shows the graph of the polynomial f(x) = ax² + bx + c, then
(a) a > 0, b < 0 and c > 0
(b) a < 0, b < 0 and c < 0
(c) a < 0, b > 0 and c > 0
(d) a < 0, b > 0 and c < 0

Solution:
(a) Curve ax² + bx + c intersects x-axis at two points and curve is upward.
a > 0, b < 0 and c> 0

Question 10.
Figure shows the graph of the polynomial f(x) = ax² + bx + c for which
(a) a < 0, b > 0 and c > 0
(b) a < 0, b < 0 and c > 0
(c) a < 0, b < 0 and c < 0
(d) a > 0, b > 0 and c < 0

Solution:
(b) Curve ax² + bx + c intersects x-axis at two points and curve is downward.
a < 0, b < 0 and c > 0

Question 11.
If the product of zeros of the polynomial f(x) = ax³ – 6x² + 11x – 6 is 4, then a =
(a) \(\frac { 3 }{ 2 }\)
(b) – \(\frac { 3 }{ 2 }\)
(c) \(\frac { 2 }{ 3 }\)
(d) – \(\frac { 2 }{ 3 }\)
Solution:
(a) f(x) = ax³ – 6x² + 11x – 6

Question 12.
If zeros of the polynomial f(x) = x³ – 3px² + qx – r are in AP, then
(a) 2p³ = pq – r
(b) 2p³ = pq + r
(c) p³ = pq – r
(d) None of these
Solution:
(a) f(x) = x³ – 3px² + qx – r
Here a = 1, b = -3p, c = q, d= -r
Zeros are in AP
Let the zeros be α – d, α, α + d

Question 13.
If the product of two zeros of the polynomial f(x) = 2x³ + 6x² – 4x + 9 is 3, then its third zero is
(a) \(\frac { 3 }{ 2 }\)
(b) – \(\frac { 3 }{ 2 }\)
(c) \(\frac { 9 }{ 2 }\)
(d) – \(\frac { 9 }{ 2 }\)
Solution:
(b)

Question 14.
If the polynomial f(x) = ax² + bx – c is divisible by the polynomial g(x) = ax² + bx + c, then ab =
(a) 1
(b) \(\frac { 1 }{ c }\)
(c) – 1
(d) – \(\frac { 1 }{ c }\)
Solution:
(a)

Question 15.
In Q. No. 14, ac =
(a) b
(b) 2b
(c) 2b2
(d) -2b
Solution:
(b) In the previous questions
Remainder = 0
(b – ac + ab²) = 0
b + ab² = ac
=> ac = b (1 + ab) = b (1 + 1) = 2b

Question 16.
If one root of the polynomial f(x) = 5x² + 13x + k is reciprocal of the other, then the value of k is
(a) 0
(b) 5
(c) \(\frac { 1 }{ 6 }\)
(d) 6
Solution:
(b)

Question 17.
If α, β, γ are the zeros of the polynomial f(x) = ax³ + bx² + cx + d, then \(\frac { 1 }{ \alpha } +\frac { 1 }{ \beta } +\frac { 1 }{ \gamma }\) =
(a) – \(\frac { b }{ d }\)
(b) \(\frac { c }{ d }\)
(c) – \(\frac { c }{ d }\)
(d) \(\frac { c }{ a }\)
Solution:
(c)

Question 18.
If α, β, γ are the zeros of the polynomial f(x) = ax³ + bx² + cx + d, then α² + β² + γ² =

Solution:
(d)

Question 19.
If α, β, γ are the zeros of the polynomial f(x) = x³ – px² + qx – r, then \(\frac { 1 }{ \alpha \beta } +\frac { 1 }{ \beta \gamma } +\frac { 1 }{ \gamma \alpha }\) =
(a) \(\frac { r }{ p }\)
(b) \(\frac { p }{ r }\)
(c) – \(\frac { p }{ r }\)
(d) – \(\frac { r }{ p }\)
Solution:
(b)

Question 20.
If α, β are the zeros of the polynomial f(x) = ax² + bx + c, then \(\frac { 1 }{ { \alpha }^{ 2 } } +\frac { 1 }{ { \beta }^{ 2 } }\) =


Solution:
(b)

Question 21.
If two of the zeros of the cubic polynomial ax³ + bx² + cx + d are each equal to zero, then the third zero is
(a) \(\frac { -d }{ a }\)
(b) \(\frac { c }{ a }\)
(c) \(\frac { -b }{ a }\)
(d) \(\frac { b }{ a }\)
Solution:
(c) Two of the zeros of the cubic polynomial ax³ + bx² + cx + d are each equal to zero
Let α, β and γ are its zeros, then

Third zero will be \(\frac { -b }{ a }\)

Question 22.
If two zeros of x³ + x² – 5x – 5 are √5 and – √5 then its third zero is
(a) 1
(b) -1
(c) 2
(d) -2
Solution:
(b)

Question 23.
The product of the zeros of x³ + 4x² + x – 6 is
(a) – 4
(b) 4
(c) 6
(d) – 6
Solution:
(c)

Question 24.
What should be added to the polynomial x² – 5x + 4, so that 3 is the zero of the resulting polynomial ?
(a) 1
(b) 2
(c) 4
(d) 5
Solution:
(b) 3 is the zero of the polynomial f(x) = x² – 5x + 4
x – 3 is a factor of f(x)
Now f(3) = (3)² – 5 x 3 + 4 = 9 – 15 + 4 = 13 – 15 = -2
-2 is to be subtracting or 2 is added

Question 25.
What should be subtracted to the polynomial x² – 16x + 30, so that 15 is the zero of the resulting polynomial ?
(a) 30
(b) 14
(b) 15
(d) 16
Solution:
(c) 15 is the zero of polynomial f(x) = x² – 16x + 30
Then f(15) = 0
f(15) = (15)² – 16 x 15 + 30 = 225 – 240 + 30 = 255 – 240 = 15
15 is to be subtracted

Question 26.
A quadratic polynomial, the sum of whose zeroes is 0 and one zero is 3, is
(a) x² – 9
(b) x² + 9
(c) x² + 3
(d) x² – 3
Solution:
(a) In a quadratic polynomial
Let α and β be its zeros
and α + β = 0
and one zero = 3
3 + β = 0 ⇒ β = -3 .
Second zero = -3
Quadratic polynomial will be
(x – 3) (x + 3) ⇒ x² – 9

Question 27.
If two zeroes of the polynomial x³ + x² – 9x – 9 are 3 and -3, then its third zero is
(a) -1
(b) 1
(c) -9
(d) 9
Solution:
(a)

=> γ = -1
Third zero = -1

Question 28.
If √5 and – √5 are two zeroes of the polynomial x³ + 3x² – 5x – 15, then its third zero is
(a) 3
(b) – 3
(c) 5
(d) – 5
Solution:
(b)

Question 29.
If x + 2 is a factor x² + ax + 2b and a + b = 4, then
(a) a = 1, b = 3
(b) a = 3, b = 1
(c) a = -1, b = 5
(d) a = 5, b = -1
Solution:
(b) x + 2 is a factor of x² + ax + 2b and a + b = 4
x + 2 is one of the factor
x = – 2 is its one zero
f(-2) = 0
=> (-2)² + a (-2) + 2b = 0
=> 4 – 2a + 2b = 0
=> 2a – 2b = 4
=> a – b = 2
But a + b = 4
Adding we get, 2a = 6 => a = 3
and a + b = 4 => 3 + b = 4 => b = 4 – 3 = 1
a = 3, b = 1

Question 30.
The polynomial which when divided by – x² + x – 1 gives a quotient x – 2 and remainder 3, is
(a) x³ – 3x² + 3x – 5
(b) – x³ – 3x² – 3x – 5
(c) – x³ + 3x² – 3x + 5
(d) x³ – 3x² – 3x + 5
Solution:
(c) Divisor = – x² + x – 1, Quotient = x – 2 and
Remainder = 3, Therefore
Polynomial = Divisor x Quotient+Remainder
= (-x² + x – 1) (x – 2) + 3
= – x³ + x² – x + 2x² – 2x + 2 + 3
= – x³ + 3x² – 3x + 5

Question 31.
The number of polynomials having zeroes -2 and 5 is
(a) 1
(b) 2
(c) 3
(d) more than 3
Solution:
(d)

Hence, the required number of polynomials are infinite i.e., more than 3.

Question 32.
If one of the zeroes of the quadratic polynomial (k – 1)x² + kx + 1 is -3, then the value of k is
(a) \(\frac { 4 }{ 3 }\)
(b) – \(\frac { 4 }{ 3 }\)
(c) \(\frac { 2 }{ 3 }\)
(d) – \(\frac { 2 }{ 3 }\)
Solution:
(a)

Question 33.
The zeroes of the quadratic polynomial x² + 99x + 127 are
(a) both positive
(b) both negative
(c) both equal
(d) one positive and one negative
Solution:
(b)

Question 34.
If the zeroes of the quadratic polynomial x² + (a + 1) x + b are 2 and -3, then
(a) a = -7, b = -1
(b) a = 5, b = -1
(c) a = 2, b = -6
(d) a = 0, b = -6
Solution:
(d)

Question 35.
Given that one of the zeroes of the cubic polynomial ax³ + bx² + cx + d is zero, the product of the other two zeroes is
(a) – \(\frac { c }{ a }\)
(b) \(\frac { c }{ a }\)
(c) 0
(d) – \(\frac { b }{ a }\)
Solution:
(b)

Question 36.
The zeroes of the quadratic polynomial x² + ax + a, a ≠ 0,
(a) cannot both be positive
(b) cannot both be negative
(c) area always unequal
(d) are always equal
Solution:
(a) Let p(x) = x² + ax + a, a ≠ 0
On comparing p(x) with ax² + bx + c, we get
a = 1, b = a and c = a

So, both zeroes are negative.
Hence, in any case zeroes of the given quadratic polynomial cannot both the positive.

Question 37.
If one of the zeroes of the cubic polynomial x³ + ax² + bx + c is -1, then the product of other two zeroes is
(a) b – a + 1
(b) b – a – 1
(c) a – b + 1
(d) a – b – 1
Solution:
(a)



=> α β = -a + b + 1
Hence, the required product of other two roots is (-a + b + 1)

Question 38.
Given that two of the zeroes of the cubic polynomial ax³ + bx² + cx + d are 0, the third zero is
(a) – \(\frac { b }{ a }\)
(b) \(\frac { b }{ a }\)
(c) \(\frac { c }{ a }\)
(d) – \(\frac { d }{ a }\)
Solution:
(a) Two of the zeroes of the cubic polynomial
ax³ + bx² + cx + d = 0, 0
Let the third zero be d
Then, use the relation between zeroes and coefficient of polynomial, we have
d + 0 + 0 = – \(\frac { b }{ a }\)
⇒ d = – \(\frac { b }{ a }\)

Question 39.
If one zero of the quadratic polynomial x² + 3x + k is 2, then the value of k is
(a) 10
(b) -10
(c) 5
(d) -5
Solution:
(b) Let the given quadratic polynomial be P(x) = x² + 3x + k
It is given that one of its zeros is 2
P(2) = 0
=> (2)² + 3(2) + k = 0 => 4 + 6 + k = 0
=> k + 10 = 0 => k = -10

Question 40.
If the zeroes of the quadratic polynomial ax² + bx + c, c ≠ 0 are equal, then
(a) c and a have opposite signs
(b) c and b have opposite signs
(c) c and a have the same sign
(d) c and b have the same sign
Solution:
(c) The zeroes of the given quadratic polynomial ax² + bx + c, c ≠ 0 are equal. If coefficient of x² and constant term have the same sign
i.e., c and a have the same sign. While b i.e., coefficient of x can be positive/negative but not zero.

Question 41.
If one of the zeroes of a quadratic polynomial of the form x² + ax + b is the negative of the other, then it
(a) has no linear term and constant term is negative.
(b) has no linear term and the constant term is positive.
(c) can have a linear term but the constant term is negative.
(d) can have a linear term but the constant term is positive.
Solution:
(a)

Given that, one of the zeroes of a quadratic polynomial p(x) is negative of the other.
αβ < 0
So, b < 0 [from Eq. (i)]
Hence, b should be negative Put a = 0, then,
p(x) = x² + b = 0 => x² = – b
=> x = ± √-b [ b < 0]
Hence, if one of the zeroes of quadratic polynomial p(x) is the negative of the other, then it has no linear term i.e., a = 0 and the constant term is negative i.e., b < 0. Alternate Method Let f(x) = x² + ax + b and by given condition the zeroes are a and -a. Sum of the zeroes = α – α = a => a = 0
f(x) = x² + b, which cannot be linear and product of zeroes = α (-α) = b
=> – α² = b
which is possible when, b < 0.
Hence, it has no linear term and the constant tenn is negative.

Question 42.
Which of the following is not the graph of a quadratic polynomial?




Solution:
(d) For any quadratic polynomial ax²+ bx + c, a 0, the graph of the corresponding equation y = ax² + bx + c has one of the two shapes either open upwards like ∪ or open downwards like ∩ depending on whether a > 0 or a < 0. These curves are called parabolas. So, option (d) cannot be possible.
Also, the curve of a quadratic polynomial crosses the X-axis on at most two points but in option (d) the curve crosses the X-axis on the three points, so it does not represent the quadratic polynomial.

Hope given RD Sharma Class 10 Solutions Chapter 2 Polynomials MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5

Other Exercises

• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.1
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.2
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.3
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.6
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers VSAQS
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS

Question 1.
Show that the following numbers are irrational
(i) \(\frac { 1 }{ \surd 2 }\)
(ii) 7 √5
(iii) 6 + √2
(iv) 3 – √5
Solution:



But it contradics that because √5 is irrational
3 – √5 is irrational

Question 2.
Prove that following numbers are irrationals :
(i) \(\frac { 2 }{ \surd 7 }\)
(ii) \(\frac { 3 }{ 2\surd 5 }\)
(iii) 4 + √2
(iv) 5 √2
Solution:




5 √2 is an irrational number

Question 3.
Show that 2 – √3 is an irrational number. [C.B.S.E. 2008]
Solution:
Let 2 – √3 is not an irrational number

√3 is a rational number
But it contradicts because √3 is an irrational number
2 – √3 is an irrational number
Hence proved.

Question 4.
Show that 3 + √2 is an irrational number.
Solution:
Let 3 + √2 is a rational number

and √2 is irrational
But our suppositon is wrong
3 + √2 is an irrational number

Question 5.
Prove that 4 – 5√2 is an irrational number. [CBSE 2010]
Solution:
Let 4 – 5 √2 is not are irrational number
and let 4 – 5 √2 is a rational number
and 4 – 5 √2 = \(\frac { a }{ b }\) where a and b are positive prime integers

√2 is a rational number
But √2 is an irrational number
Our supposition is wrong
4 – 5 √2 is an irrational number

Question 6.
Show that 5 – 2 √3 is an irrational number.
Solution:
Let 5 – 2 √3 is a rational number
Let 5 – 2 √3 = \(\frac { a }{ b }\) where a and b are positive integers

and √3 is a rational number
Our supposition is wrong
5 – 2 √3 is a rational number

Question 7.
Prove that 2 √3 – 1 is an irrational number. [CBSE 2010]
Solution:
Let 2 √3 – 1 is not an irrational number
and let 2 √3 – 1 a ration number
and then 2 √3 – 1 = \(\frac { a }{ b }\) where a, b positive prime integers

√3 is a rational number
But √3 is an irrational number
Our supposition is wrong
2 √3 – 1 is an irrational number

Question 8.
Prove that 2 – 3 √5 is an irrational number. [CBSE 2010]
Solution:
Let 2 – 3 √5 is not an irrational number and let 2 – 3 √5 is a rational number
Let 2 – 3 √5 = \(\frac { a }{ b }\) where a and b are positive prime integers

\(\Longrightarrow \frac { 2b-a }{ 3b } =\surd 5\)
√5 is a rational
But √5 is an irrational number
Our supposition is wrong
2 – 3 √5 is an irrational

Question 9.
Prove that √5 + √3 is irrational.
Solution:
Let √5 + √3 is a rational number
and let √5 + √3 = \(\frac { a }{ b }\) where a and b are co-primes

√3 is a rational number
But it contradics as √3 is irrational number
√5 + √3 is irrational

Question 10.
Prove that √2 + √3 is an irrational number.
Solution:
Let us suppose that √2 + √3 is rational.
Let √2 + √3 = a, where a is rational.
Therefore, √2 = a – √3
Squaring on both sides, we get

which is a contradiction as the right hand side is a rational number while √3 is irrational.
Hence, √2 + √3 is irrational.

Question 11.
Prove that for any prime positive integer p, √p is an irrational number.
Solution:
Suppose √p is not a rational number
Let √p be a rational number
and let √p = \(\frac { a }{ b }\)
Where a and b are co-prime number


But it contradicts that a and b are co-primes
Hence our supposition is wrong
√p is an irrational

Question 12.
If p, q are prime positive integers, prove that √p + √q is an irrational number
Solution:


Hence proved.

Hope given RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4

Other Exercises

• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.1
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.2
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.3
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.5
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.6
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers VSAQS
• RD Sharma Class 10 Solutions Chapter 1 Real Numbers MCQS

Question 1.
Find the L.C.M. and H.C.F. of the following pairs of integers and verify that L.C.M. x H.C.F. = Product of the integers.
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Solution:
(i) 26 and 91
26 = 2 x 13
91 = 7 x 13
H.C.F. = 13
and L.C.M. = 2 x 7 x 13 = 182
Now, L.C.M. x H.C.F. = 182 x 13 = 2366
and 26 x 91 = 2366
L.C.M. x H.C.F. = Product of integers

Question 2.
Find the L.C.M. and H.C.F. of the following integers by applying the prime factorisation method :
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
(iv) 40, 36 and 126
(v) 84, 90 and 120
(vi) 24,15 and 36
Solution:

Question 3.
Given that HCF (306, 657) = 9, Find LCM (306, 657). [NCERT]
Solution:
HCF of 306, 657 = 9

Question 4.
Can two numbers have 16 as their H.C.F. and 380 as their L.C.M. ? Give reason.
Solution:
H.C.F. of two numbers = 16
and their L.C.M. = 380

We know the H.C.F. of two numbers is a factor of their L.C.M. but 16 is not a factor of 380 or 380 is not divisible by 16
It can not be possible.

Question 5.
The H.C.F. of two numbers is 145 and their L.C.M. is 2175. If one number is 725, find the other.
Solution:
First number = 725
Let second number = x
Their H.C.F. = 145
and L.C.M. = 2175

Second number = 435

Question 6.
The H.C.F. of two numbers is 16 and their product is 3072. Find their L.C.M.
Solution:
H.C.F. of two numbers = 16
and product of two numbers = 3072

Question 7.
The L.C.M. and H.C.F. of two numbers are 180 and 6 respectively. If one of the number is 30, find the other number.
Solution:
First number = 30
Let x be the second number
Their L.C.M. = 180 and H.C.F. = 6
We know that
first number x second number = L.C.M. x H.C.F.
30 x x = 180 x 6
⇒ x = \(\frac { 180\times 6 }{ 30 }\) = 36
Second number = 36

Question 8.
Find the smallest number which when increased by 17 is exactly divisible by both 520 and 468.
Solution:
L.C.M. of 520 and 468

= 2 x 2 x 9 x 10 x 13 = 4680
The number which is increased = 17
Required number 4680 – 17 = 4663

Question 9.
Find the smallest number which leaves remainders 8 and 12 when divided by 28 and 32 respectively.
Solution:
Dividing by 28 and 32, the remainders are 8 and 12 respectively
28 – 8 = 20
32 – 12 = 20
Common difference = 20
Now, L.C.M. of 28 and 32

= 2 x 2 x 7 x 8 = 224
Required smallest number = 224 – 20 = 204

Question 10.
What is the smallest number that, when divided by 35, 56 and 91 leaves remainders of 7 in each case ?
Solution:
L.C.M. of 35, 56, 91

= 5 x 7 x 8 x 13 = 3640
Remainder in each case = 7
The required smallest number = 3640 + 7 = 3647

Question 11.
A rectangular courtyard is 18 m 72 cm long and 13 m 20 cm broad. It is to be paved with square tiles of same size. Find the least possible number of such tiles.
Solution:
Length of rectangle = 18 m 72 cm = 1872 cm
and breadth = 13 m 20 cm = 1320 cm
Side of the greatest size of square tile = H.C.F. of 1872 and 1320

Question 12.
Find the greatest number of 6 digits exactly divisible by 24, 15 and 36.
Solution:
Greatest number of 6 digits = 999999
Now L.C.M. of 24, 15 and 36

We get quotient = 2777
and remainder = 279
Required number = 999999 – 279 = 999720

Question 13.
Determine the number nearest to 110000 but greater than 100000 which is exactly divisible by each of 8, 15 and 21.
Solution:

Required number will be = 110000 – 800 =109200

Question 14.
Find the least number that is divisible by ail the numbers between 1 to 10 (both inclusive).
Solution:
The required least number which is divisible by 1 to 10 will be the L.C.M. of 1 to 10
L.C.M. of 1 to 10

Question 15.
A circular field has a circumference of 360 km. Three cyclists start together and can cycle 48, 60 and 72 km a day, round the field. When will they meet again ?
Solution:
Circumference of a circular field = 360 km
Three cyclist start together who can cycle 48, 60 and 72 km per day round the field
L.C.M. of 48, 60, 72

They will meet again after 720 km distance

Question 16.
In a morning walk, three persons step off together, their steps measure 80 cm, 85 cm and 90 cm respectively. What is the minimum distance each should walk so that they can cover the distance in complete steps ?
Solution:
Measures of steps of three persons = 80 cm, 85 cm and 90 cm
Minimum required distance covered by them = L.C.M. of 80 cm, 85 cm, 90 cm

= 2 x 5 x 8 x 9 x 17
= 12240 cm
= 122.40 m
= 122 m 40 cm

Hope given RD Sharma Class 10 Solutions Chapter 1 Real Numbers Ex 1.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.