Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.
Emulsions
Emulsions are colloidal solution in which a liquid is dispersed in an another liquid. Generally there are two types of emulsions.
- Oil in water (O/W)
- Water in oil (W/O)
Example:
- Milk is example of the oil in water type emulsion.
- Stif greases are emulsion of water in oil i.e. water dispersed in lubricating oil.
- The process of preparation of emulsion by the dispersal of one liquid in another liquid is called Emulsification.
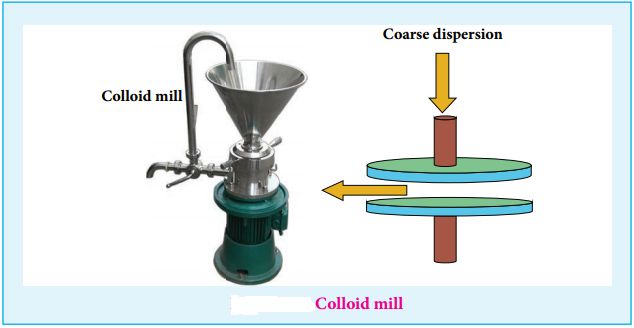
- A colloid mill can be used as a homogeniser to mix the two liquid. To have a stable emulsion a small amount of emulsifier or emulsification agent is added.
Several Types of Emulsifiers are known.
- Most of the lyophillic colloids also act as emulsifiers. Example: glue, gelatine.
- Long chain compounds with polar groups like soap and sulphonic acids.
- Insoluble powders like clay and lamp black also act as emulsifiers.
Identification of Types of Emulsion
The two types of emulsions can be identified by the following tests.
(i) Dye Test
A small amount of dye soluble in oil is added to the emulsion. The emulsion is shaken well. The aqueous emulsion will not take the colour whereas oily emulsion will take up the colour of the dye.
(ii) Viscosity Test
Viscosity of the emulsion is determined by experiments. Oily emulsions will have higher value than aqueous emulsion.
(iii) Conductivity Test
Conductivity of aqueous emulsions are always higher than oily emulsions.
(iv) Spreading Test
Oily emulsions spread readily than aqueous emulsion when spread on an oily surface.
Deemulsification:
Emulsion can be separated into two separate layers. The process is called Deemulsification.
Various Deemulsification Techniques are Given Below
- Distilling of one component
- Adding an electrolyte to destroy the charge
- Destroying the emulsifir using chemical methods
- Using solvent extraction to remove one component
- By freezing one of the components
- By applying centrifugal force
- Adding dehydrating agents for water in oil (W/O) type
- Using ultrasonic waves.
- Heating at high pressures.
Inversion of Phase:
The change of W/O emulsion into O/W emulsion is called inversion of phases.
For example:
An oil in water emulsion containing potassium soap as emulsifying agent can be converted into water in oil emulsion by adding CaCl2 or AlCl3. The mechanism of inversion is in the recent developments of research.

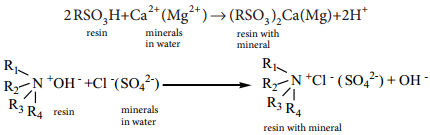
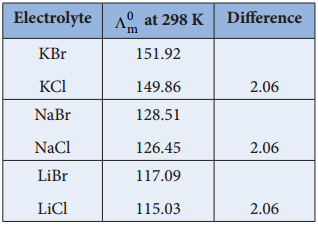
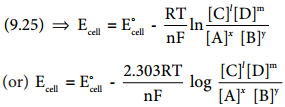 ………… (9.31)
………… (9.31)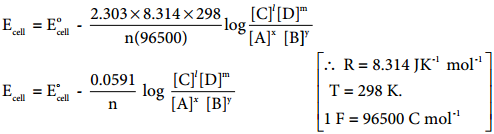 ……………… (9.32)
……………… (9.32)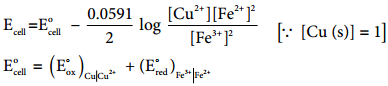
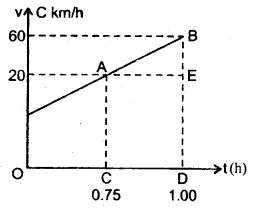
 …………… (9.35)
…………… (9.35)
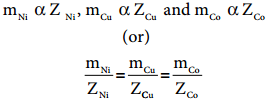 ………….. (9.36)
………….. (9.36)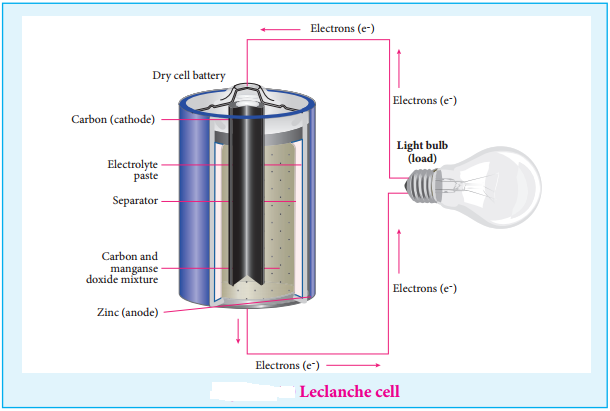
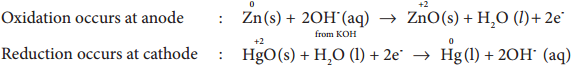
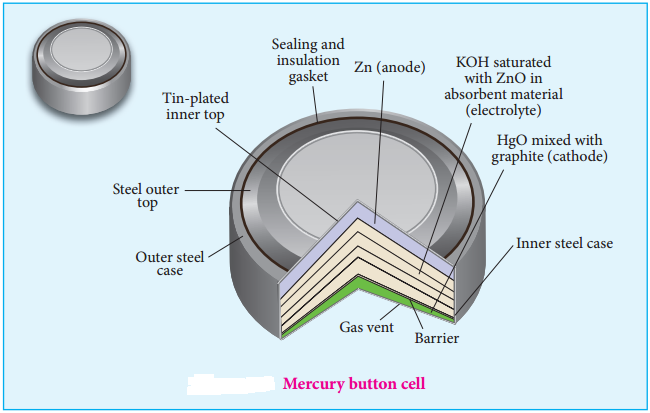

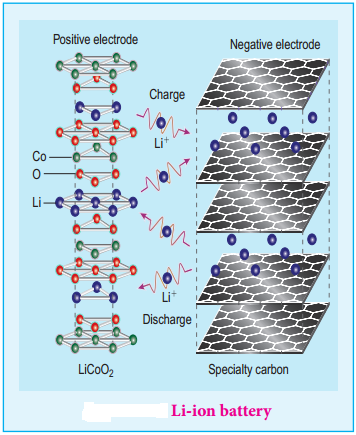
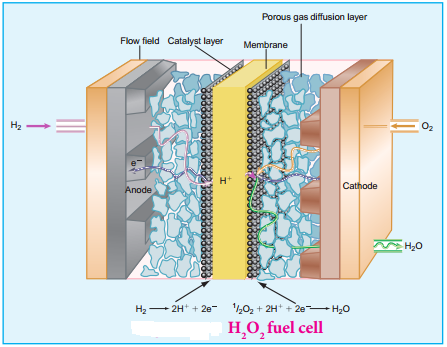
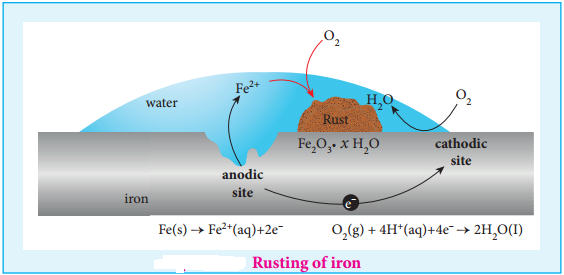
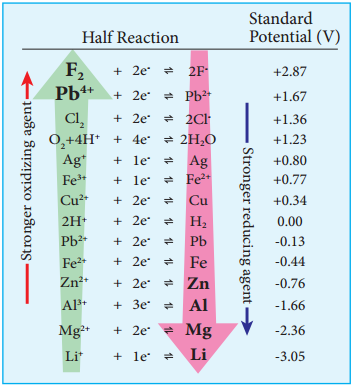
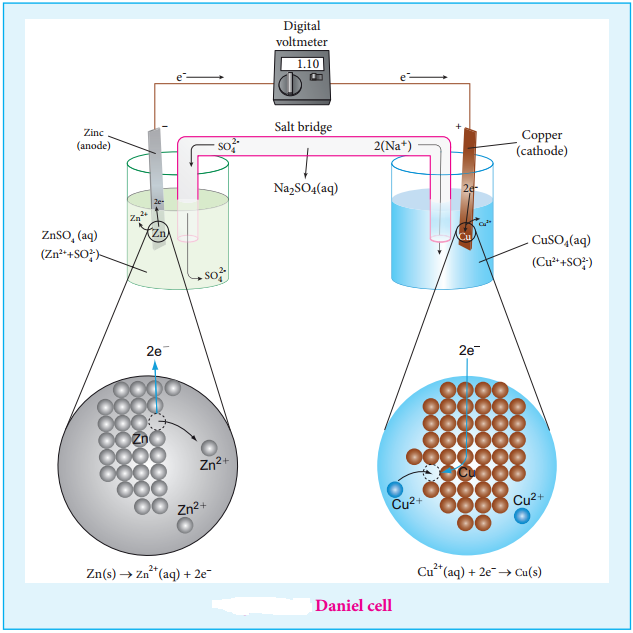
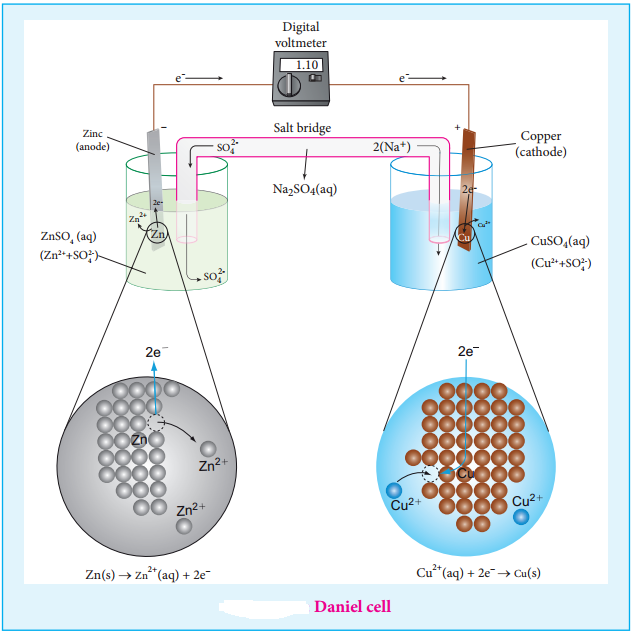
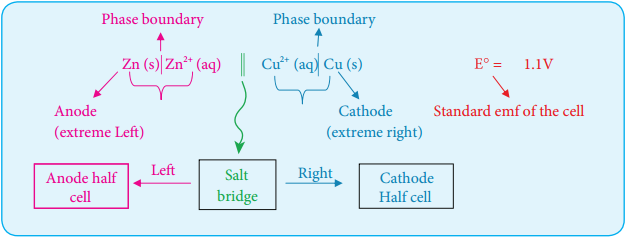
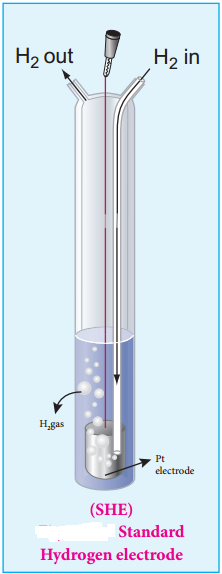
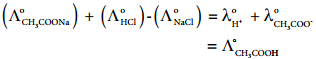
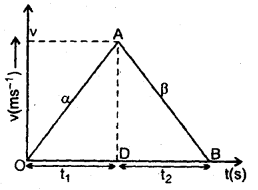
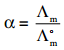 ………… (9.14)
………… (9.14)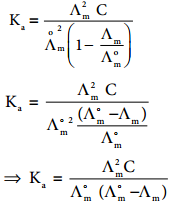
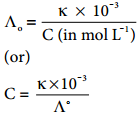
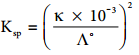 ………… (9.17)
………… (9.17)
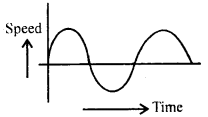
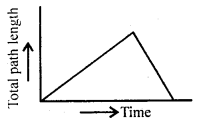
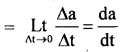
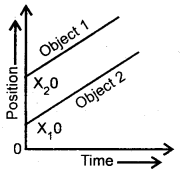
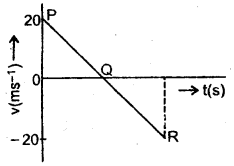
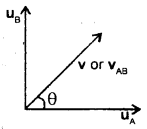
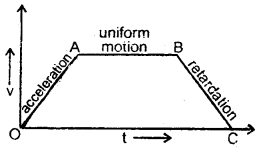
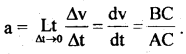
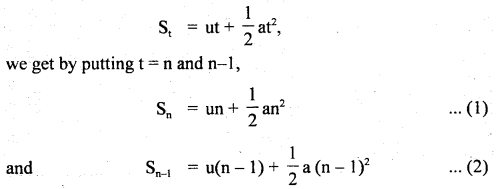
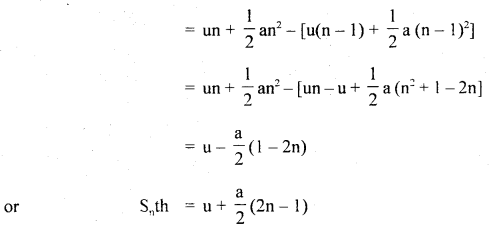
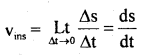
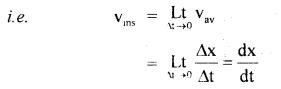
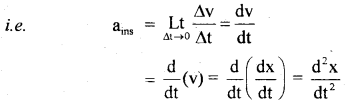
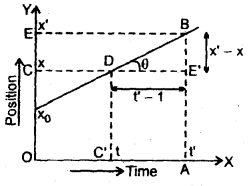
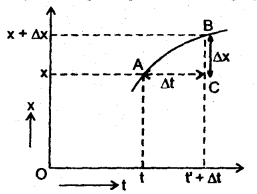
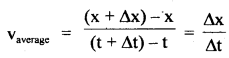
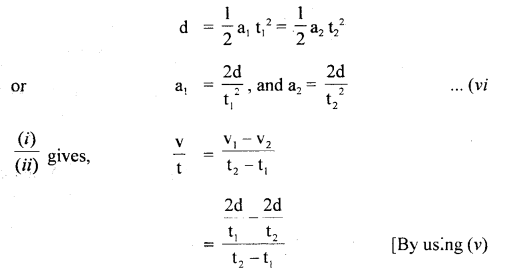
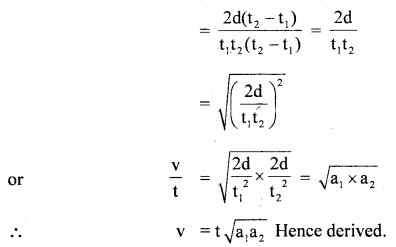
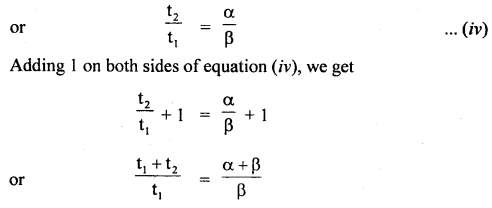

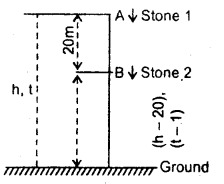
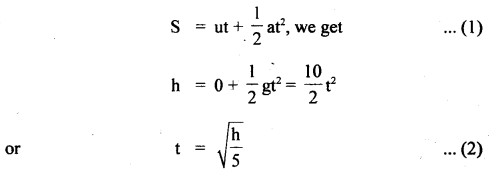
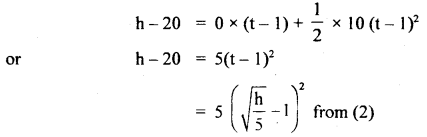

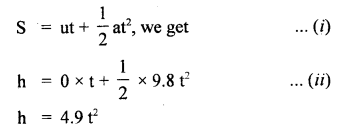
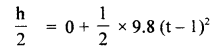

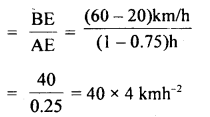

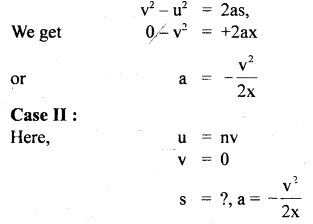
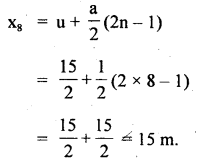
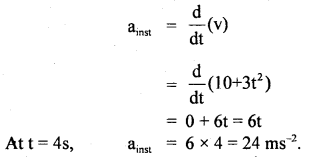

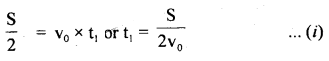
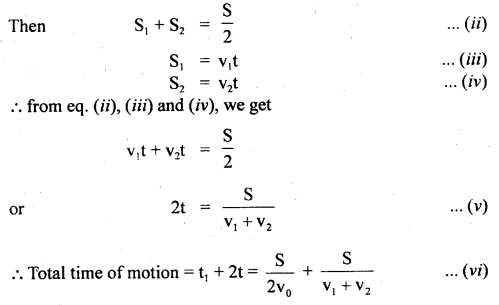




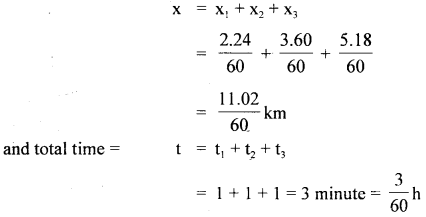


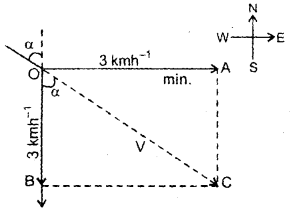
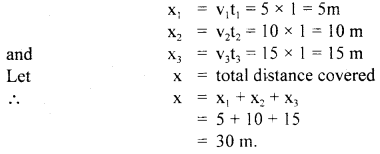
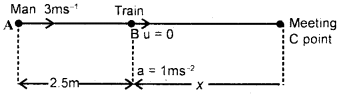

 im-90
im-90