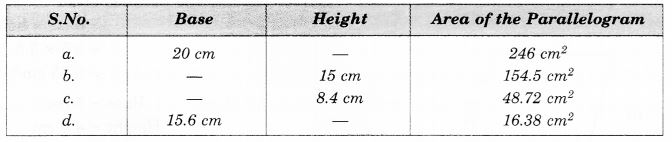
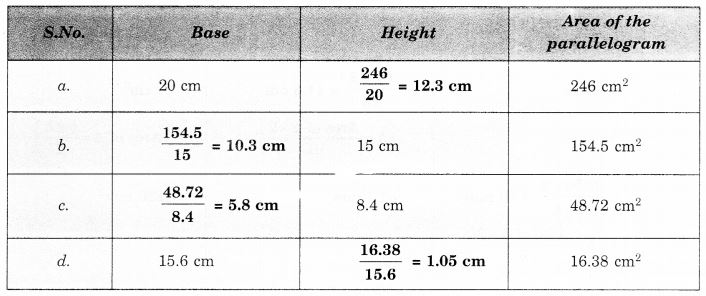
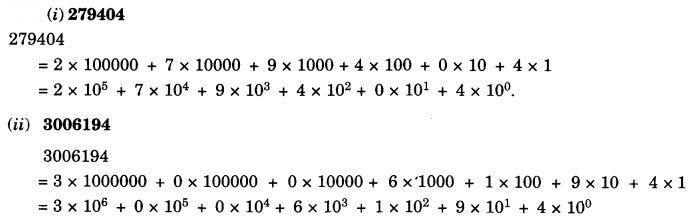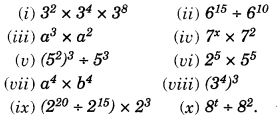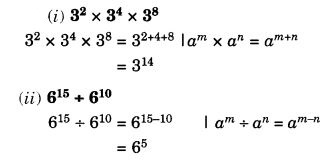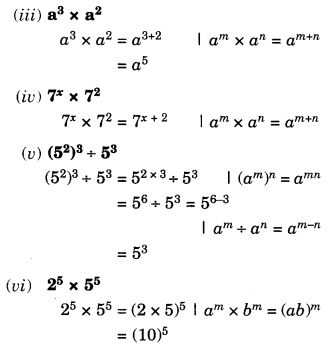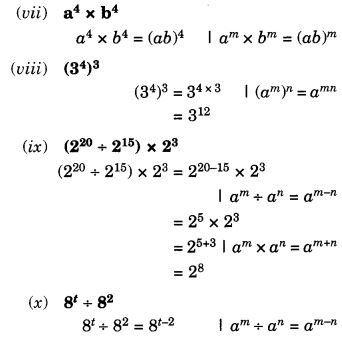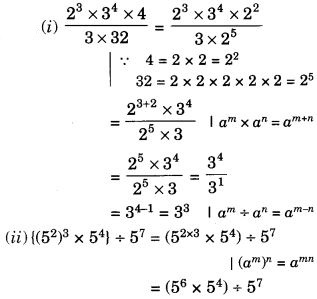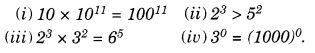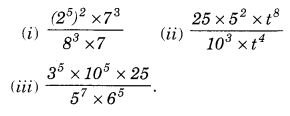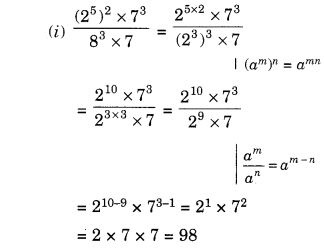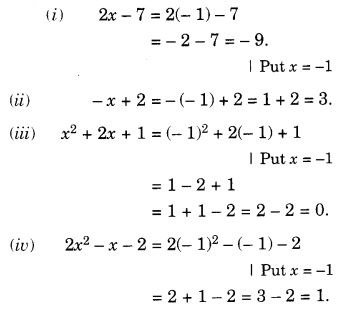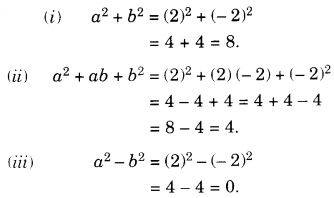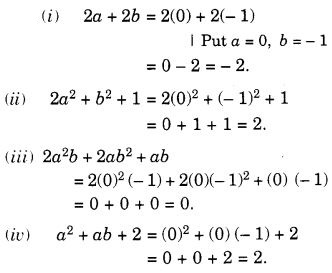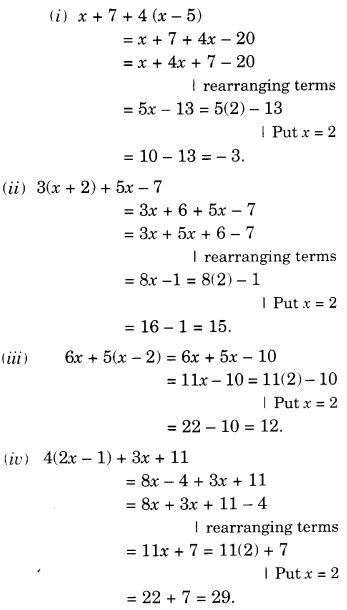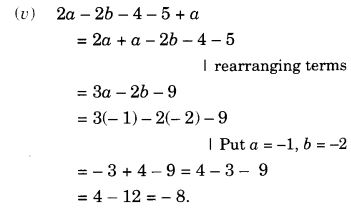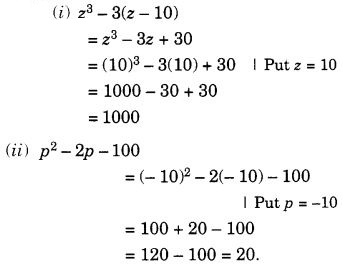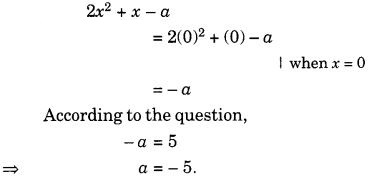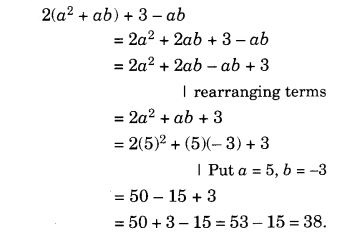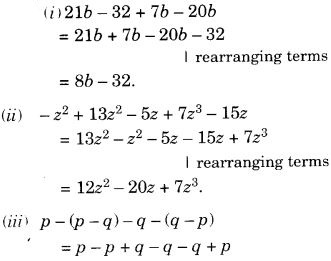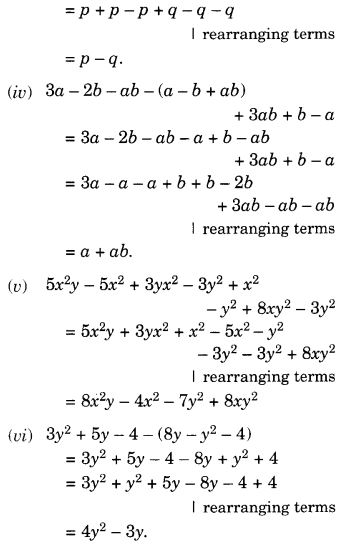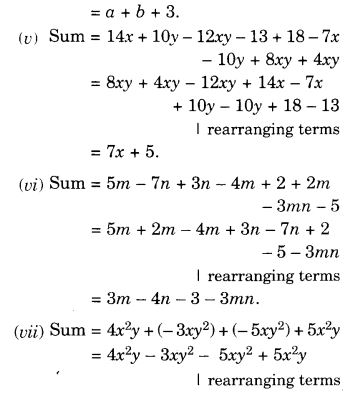NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Ex 14.2 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Ex 14.2.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 7 |
| Subject | Maths |
| Chapter | Chapter 14 |
| Chapter Name | Symmetry |
| Exercise | Ex 14.2 |
| Number of Questions Solved | 2 |
| Category | NCERT Solutions |
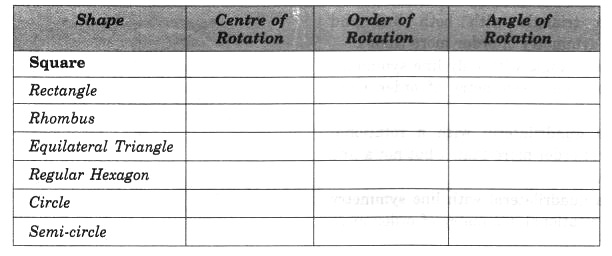
NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Ex 14.2
Question 1.
Which of the following figures have rotational symmetry of order more than 1?
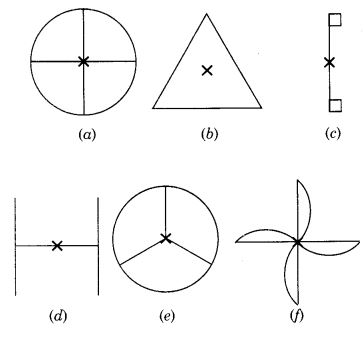
Solution:
Figures (a), (b), (d), (e) and (f) have rotational symmetry of order more than 1.
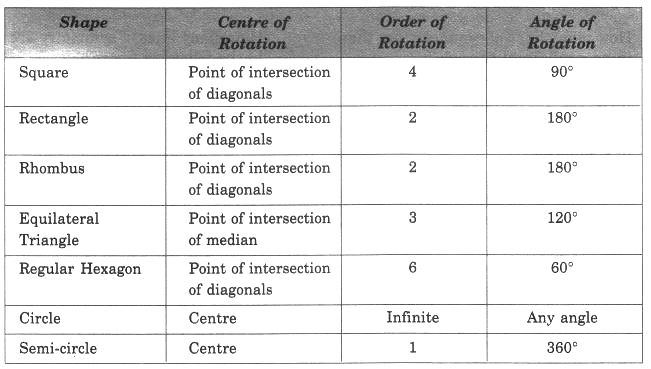
Question 2.
Give the order of rotational symmetry for each figure :
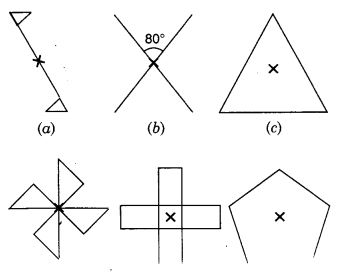
Solution:
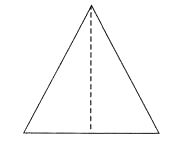
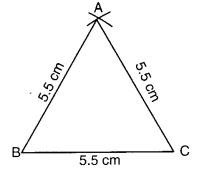
(a) → 2
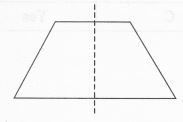
(b) → 2
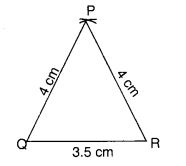
(c) → 3
(d) → 4
(e) → 4
(f) → 5
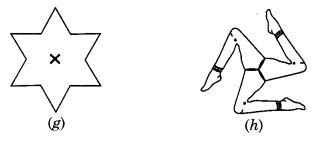
(g) → 6
(h) → 3
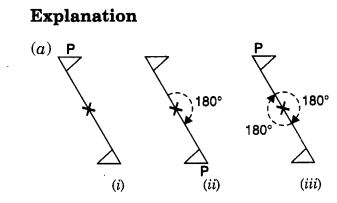
Mark a point P as shown in figure (i). We see that in a full turn, there are two positions (on rotation through the angles 180° and 360°) when the figure looks exactly the same. Because of this, it has rotational symmetry of order 2.

Mark a point P as shown in figure (i). We see that in a full turn, there are two positions (on rotation through the angles 180° and 360°) when the figure looks exactly the same.
Because of this, it has rotational symmetry of order 2.
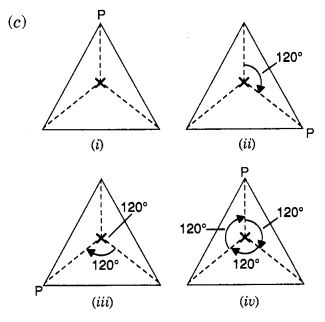
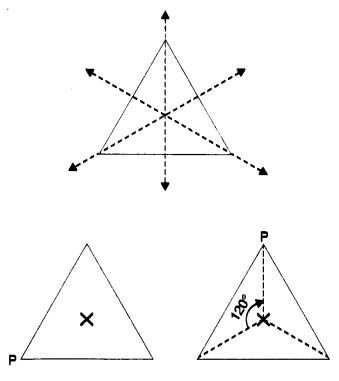
Mark a point P as shown in figure (i). We see that in a full turn, there are three positions (on rotation through the angles 120°, 240°, and 360°) when the figure looks exactly the same. Because of this, it has rotational symmetry of order 3.
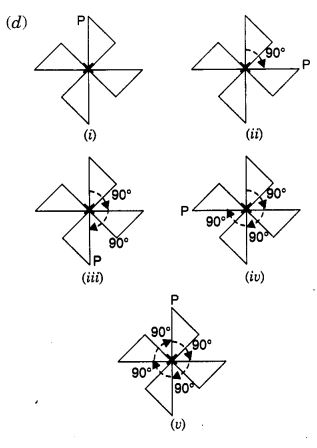
Mark a point P as shown in figure (i). We see that in a full turn, there are four positions (on rotation through the angles 90°, 180°, 270°, and 360°) when the figure looks exactly the same. Because of this, we say that it has rotational symmetry of order 4.
Similarly,
(e) In a full turn, there are four positions (on rotation through the angles 90°, 180°, 270°, and 360°) when the figure looks exactly the same.
∴ It has rotational symmetry of order 4.
(f) The figure is a regular pentagon. In a full turn, there are five positions (on rotation through the angles 72°, 144°, 216°, 288°, and 360°) when the figure looks exactly the same.
∴ It has rotational symmetry of order 5.
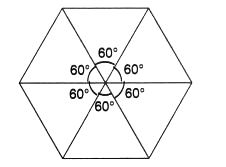
(g) In a full turn, there are six positions (on rotation through the angles 60°, 120°, 180°, 240°, 300°, and 360°) when the figure looks exactly the same.
It has rotational symmetry of order 6.
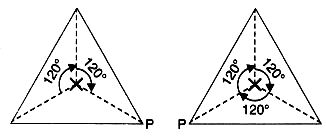
(h) In a full turn, there are three positions (on rotation through the angles 120°, 240°, and 360°) when the figure looks exactly the same.
∴ It has rotational symmetry of order 3.
We hope the NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Ex 14.2 helps you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 14 Symmetry Ex 14.2, drop a comment below and we will get back to you at the earliest.