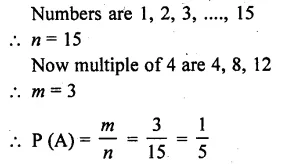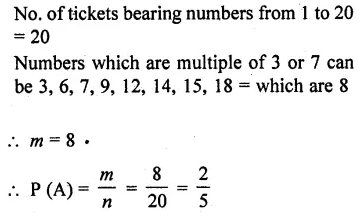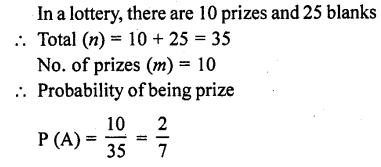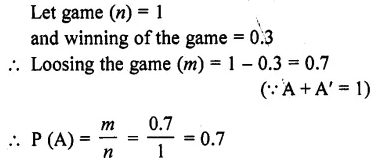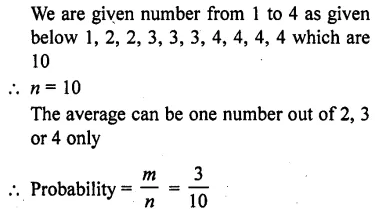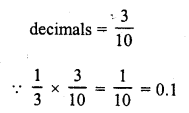RD Sharma Class 10 Solutions Chapter 16 Probability Ex VSAQS
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 16 Probability VSAQS
Other Exercises
- RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.1
- RD Sharma Class 10 Solutions Chapter 16 Probability Ex 16.2
- RD Sharma Class 10 Solutions Chapter 16 Probability Ex VSAQS
- RD Sharma Class 10 Solutions Chapter 16 Probability Ex MCQS
Question 1.
Cards each marked with one of the numbers 4, 5, 6, …….. 20 are placed in a box and mixed thoroughly. One card is drawn at random from the box what is the probability of getting an even number ?
Solution:

Question 2.
One card is drawn from a well shuffled deck of 52 playing cards. What is the probability of getting a non-face card ?
Solution:

Question 3.
A bag contains 5 red, 8 green and 7 white balls. One ball is drawn at random from the bag. What is the probability of getting a white ball or a green ball ?
Solution:

Question 4.
A die is thrown once. What is the probability of getting a prime number?
Solution:
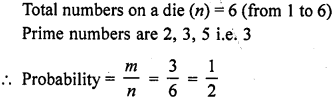
Question 5.
A die is thrown once. What is the probability of getting a number lying between 2 and 6 ?
Solution:
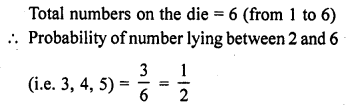
Question 6.
A die is thrown once. What is the probability of getting an odd number ?
Solution:
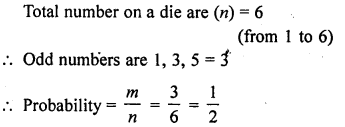
Question 7.
If \(\bar { E }\) denoted the complement or negation of an even E, what is the value of P(E) + P(\(\bar { E }\))?
Solution:

Question 8.
One card is drawn at random from a well shuffled deck of 52 cards. What is the probability of getting an ace ?
Solution:

Question 9.
Two coins are tossed simultaneously. What is the probability of getting at least one head ?
Solution:

Question 10.
Tickets numbered 1 to 20 are mixed up and then a ticket is drawn at random. What is the probability that the ticket drawn bears a number which is a multiple of 3?
Solution:

Question 11.
From a well shuffled pack of cards, a card is drawn at random. Find the probability of getting a black queen.[C.B.S.E. 2008]
Solution:
![]()

Question 12.
A die is thrown once. Find the probability of getting a number less than 3. [CBSE 2008]
Solution:
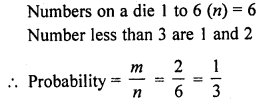
Question 13.
Two coines are tossed simultaneously. Find the probability of getting exactly one head. [CBSE 2009]
Solution:

Question 14.
A die is thrown once. What is the probability of getting a number greater than 4 ? [CBSE 2010]
Solution:
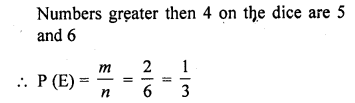
Question 15.
What is the probability that a number selected at random from the numbers 3, 4, 5,…, 9 is a multiple of 4 ? [CBSE 2010]
Solution:
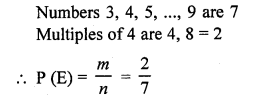
Question 16.
A letter of English alphabet is chosen at random. Determine the probability that the chosen letter is a consonant.
Solution:

Question 17.
A bag contains 3 red and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is not red? [CBSE 2017]
Solution:

Question 18.
A number is chosen at random from the numbers, -3, -2, -1, 0,1, 2, 3. What will be the probability that the square of this number is less than or equal tori?
Solution:
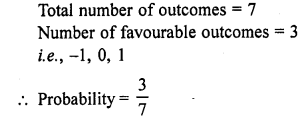
Hope given RD Sharma Class 10 Solutions Chapter 16 Probability VSAQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.