Category: CBSE Class 6

RS Aggarwal Class 6 Solutions Chapter 13 Angles and Their Measurement Ex 13A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13A.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13A
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13B
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13C
• RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13D

Question 1.
Solution:
Three examples are : Tongs, Scissors and Compasses.

Question 2.
Solution:
In the given angle ABC, the vertex is B and arms are \(\overrightarrow { AB } \) and \(\overrightarrow { BC } \) .

Question 3.
Solution:
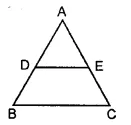
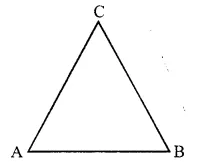
(i) In the given figure, three angles are formed.

Names of the angles are :
∠ABC, ∠BAC and ∠ACB
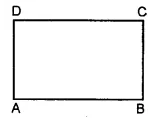
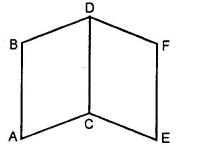
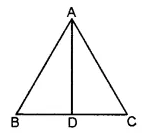
(ii) In the given figure, four angles are formed.

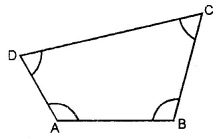
∠ABC, ∠BCD, ∠CDA and ∠BAD
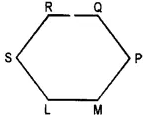
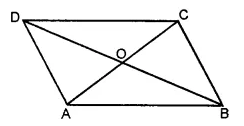
(iii) In the given figure, eight angles are formed.

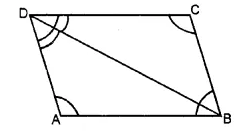
Names of the angles are :
∠ABC, ∠BCD, ∠CDA, ∠BAD, ∠ABD, ∠DCB, ∠ADB and ∠BDC

Question 4.
Solution:
In given figure
(i) Points S and Q are in the interior of ∠AOB
(ii) Points P and R are in the exterior of ∠AOB.
(iii) Points A, O, B, N, T lie on ∠AOB.

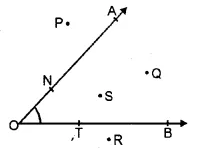
Question 5.
Solution:
(i) False
(ii) True
(iii) False
(iv) True
(v) False

Question 6.
Solution:
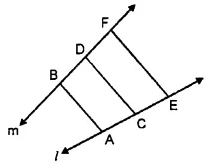
In the given figure, another name for :
(i) ∠1 is ∠EPB
(ii) ∠2 is ∠PQC
(iii) ∠3 is FQD

 

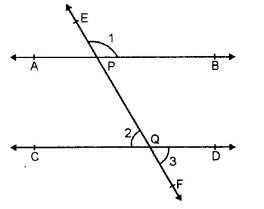
Hope given RS Aggarwal Solutions Class 6 Chapter 13 Angles and Their Measurement Ex 13A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 12 Parallel Lines Ex 12

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 12 Parallel Lines Ex 12.

Question 1.
Solution:
In the given figure, the pairs of parallel edges are :
AB || CD and BC || AD

Question 2.
Solution:
In the given figure, pairs of all possible parallel edges are:
AB | | HE | | DC || GF ; BE | | CF || AH
| | DG ; AD | | GH | | BC | | EF

Question 3.
Solution:
(i) In the given figure,
DE || BC

(ii) In the given figure,
AB || DC ; AD || BC

(iii) In the given figure,
AB || DC ; AD || BC

(iv) In the given figure,
LM || RQ, MP || RS, PQ || SL.

(v) In the given figure,
AB || CD, CD || EF, AC || BD, CE || DF, AB || EF.

Question 4.
Solution:
(i) Place the rular so that one of its measuring edges lies along the line. Hold it firmly with one hand. Now place a set square with one arm of the right angle coinciding with the edge of the rular. Read off the distance between i and m on the set square which is 1.7cm.

(ii) Place the rular so that one of the measuring edges of the rular lies along the line /. Hold it firmly with one hand and place a set square with one arm of the right angle coinciding with the edge of the rular. Read off the distance between the lines / and m on the set square which is 1.2 cm.

Question 5.
Solution:
It is given that l || m.
Also AB ⊥ l i.e. AB is the perpendicular distance between two parallel lines l and m.
Again CD ⊥ l i.e. CD is the perpendicular distance between two parallel lines l and m.
But the perpendicular distance between two parallel lines is always same everywhere.
CD = AB = 2.3 cm.

Question 6.
Solution:
In the given figure, we see that the line segments AB and CD do not intersect. But, the corresponding lines determined by them will clearly intersect. So, the segment AB and CD are not parallel.

Question 7.
Solution:
(i) Place the rular so that one of its measuring edges lies along of its measuring edges lies along the line l. Hold it firmly and place a set square with one arm of the right angle coinciding with the edge of the rular. Draw the line segment AB along the edge of the set square as shown in figure.

Slide the set square along the rular and draw some more segments CD and EF. We observe that AB = CD = EF.
l || m.
(ii) Place the rular so that one of its measuring edges lies along the line l. Hold it firmly and place a set square with one arm of the right angle conciding with the edge of the rular. Draw the line segment AB along the edge of the set square.

Slide the set square along the rular and draw some more segments CD and EF as shown in the figure.
We observe that AB ≠ CD ≠ EF
Hence l is not parallel to m.

Question 8.
Solution:
(i) True
(ii) True
(iii) False
(iv) False.

 

Hope given RS Aggarwal Solutions Class 6 Chapter 12 Parallel Lines Ex 12 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 11 Line Segment, Ray and Line Ex 11B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11B.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11A
• RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11B

Mark against the correct answer in each of following.

Question 1.
Solution:
(c) a line has no end points

Question 2.
Solution:
(b) a ray has no end points

Question 3.
Solution:
(a) a line segment has two end points

Question 4.
Solution:
(b) a line segment has definite length

Question 5.
Solution:
(b) a line segment can be drawn on a piece of paper

Question 6.
Solution:
(d) unlimited number can be drawn passing through a given point

Question 7.
Solution:
(a) one only can be drawn passing through two given points

Question 8.
Solution:
Two planes intersect in a line. (c)

Question 9.
Solution:
Two lines intersect at a point. (a)

Question 10.
Solution:
Two points in a plane determine exactly one line segment. (a)

Question 11.
Solution:
The minimum number of points of intersection of three lines in a plane is 0.(d)

Question 12.
Solution:
The maximum number of a points of intersection of three lines in a plane is 3 (d)

Question 13.
Solution:
Every line segment has a definite length. (c)

Question 14.
Solution:
Ray \(\overrightarrow { AB } \) not same as ray \(\overrightarrow { BA } \) Both are different. Hence \(\overrightarrow { AB } \) same as \(\overrightarrow { BA } \) is false.(b)

Question 15.
Solution:
An unlimited number of rays can be drawn with a given point as the initial point. (c)

Hope given RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 11 Line Segment, Ray and Line Ex 11A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11A.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11A
• RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11B

Question 1.
Solution:
Line segment
(i) In figure (i) are \(\overline { XY } \) and \(\overline { YZ } \)
(ii) In figure (ii) \(\overline { AD } ,\overline { AB } ,\overline { AC } ,\overline { AE } ,\overline { BD } ,\overline { BC } ,\overline { CE } \)
(iii) In figure (iii) \(\overline { PQ } ,\overline { PR } ,\overline { PS } ,\overline { QR } ,\overline { QS } ,\overline { RS } \)

Question 2.
Solution:
(i) In fig. (i), line segments is \(\overline { AB } \), and
rays are \(\overrightarrow { AC }\) and \(\overrightarrow { BD }\).
(ii) In fig. (ii), line segments are
\(\overline { GE } ,\overline { GP } ,\overline { EP } \) and rays are
\(\overrightarrow { EF } ,\overrightarrow { GH } ,\overrightarrow { PQ }\)
(iii) In fig. (iii), line segments are \(\overline { OL } ,\overline { OP } \)
and rays are \(\overrightarrow { LM } ,\overrightarrow { PQ } \).

Question 3.
Solution:
(i) Four line segments are \(\overline { PR } ,\overline { QR } ,\overline { PQ } ,\overline { RS } \).
(ii) Four ray can be \(\overrightarrow { PA },\overrightarrow { QC }, \overrightarrow { RB } ,\overrightarrow { SD } \)
(iii) \(\overline { PR } ,\overline { QS } \) are two non-intersecting lines.

Question 4.
Solution:
(i) Three or more points in a plane are said to be collinear if they all lie on the same line.

(ii) In the figure given above, points A, B, C are collinear points.
We can draw exactly one line passing through three collinear points

Question 5.
Solution:
(i) Four pairs of intersecting lines are : (AB, PQ) ; (AB, RS) ; (CD, PQ) ; (CD, RS)
(ii) Four collinear points are : A, Q, S, B
(iii) Three non-collinear points are : A, Q, P
(iv) Three concurrent lines are : AB, PS and RS.
(v) Three lines whose point of intersection is P are : CD, PQ and PS.

Question 6.
Solution:
The lines drawn through given points A, B, C are as shown below. The names of these lines are AB, BC and AC.

Also it is clear that three different lines can be drawn.

Question 7.
Solution:
(i) In the the given figure, there are six line segments, namely AB, AC, AD, BD, BC, DC.

(ii) In the given figure, there are ten line segments, namely, AD, AB, AC, AO, OC, BC, BD, BO, OD, CD.

(iii) In the given figure, there are six line segments, namely AB, AF, BF, CD, DE, CE.

(iv) In the given figure, there are twelve line segments, namely, AB, BC, CD, AD, BF, CG, DH, AE, EF, FG, GH, EH.

Question 8.
Solution:
\(\overleftrightarrow { PQ } \) is a line

(i) False, as M does not lie on \(\overrightarrow { NQ } \)
(ii) True
(iii) True
(iv) True
(v) True

Question 9.
Solution:
(i) False
Point has no dimensions.
(ii) False
A line segment has a length.
(iii) False
A ray has no finite length.
(iv) False
If \(\overrightarrow { AB } \) and ray \(\overrightarrow { BA } \) have opposite directions.
(v) True
Length of \(\overline { AB } \) and \(\overline { BA } \) is same.
(vi) True
Line \(\overleftrightarrow { AB } \) and \(\overleftrightarrow { BA } \) are same.
(vii) True
Distance between A and B or B and A is same, so they determine a unique line segment.
(viii) True
Two lines intersect each other at one point.
(ix) False
Two intersecting planes intersect at one line not at one point.
(x) False
If A, B, C are collinear and points D, E are collinear then it is not necessary that there points A, B, C, D and E are collinear.
(xi) False
Infinite number of rays can be drawn with a given end point.
(xii) True
We can draw one and only one line passing through two given points.-
(xiii) True
We can draw infinite number of lines pass through a given point.

Question 10.
Solution:
(i) definite
(ii) one
(iii) no
(iv) definite
(v) cannot. Ans.

 

Hope given RS Aggarwal Solutions Class 6 Chapter 11 Line Segment, Ray and Line Ex 11A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10D

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10D.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10A
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10B
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10C
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10D

OBJECTIVE QUESTIONS
Mark against the correct answer in each of the following :

Question 1
Solution:
(d) \(\\ \frac { 92 }{ 115 } \)

Question 2.
Solution:
(a) \(\\ \frac { 57 }{ x } \)
= \(\\ \frac { 51 }{ 85 } \)

Question 3.
Solution:
(a) \(\\ \frac { 25 }{ 35 } \)
= \(\\ \frac { 45 }{ x } \)

Question 4.
Solution:
(c) \(\\ \frac { 4 }{ 5 } \)
= \(\\ \frac { x }{ 35 } \)

Question 5.
Solution:
(b) \(\\ \frac { a }{ b } \)
= \(\\ \frac { c }{ d } \)
=>ad = bc

Question 6.
Solution:
(b) a : b :: b : c

Question 7.
Solution:
(b) \(\\ \frac { 5 }{ 8 } \) < \(\\ \frac { 3 }{ 4 } \) => 4 x 5 < 3 x 8 => 20 < 24

Question 8.
Solution:
Total amount = Rs 760
Ratio A : B = 8 : 11

Question 9.
Solution:
(d) largest = \(\\ \frac { 252\times 7 }{ 5+7 } \)
= \(\\ \frac { 252\times 7 }{ 12 } \)
= 21 x 7
= 147

Question 10.
Solution:
(b) largest = \(\\ \frac { 90\times 5 }{ 1+3+5 } \)
= \(\\ \frac { 90\times 5 }{ 9 } \)
= 50 cm

Question 11.
Solution:
(c) total strength of school
largest = \(\\ \frac { 840 }{ 5 } \) x (12 + 5)
= \(\\ \frac { 840\times 17 }{ 5 } \)
= 168 x 17
= 2856

Question 12.
Solution:
(b) Cost of 12 pens = Rs 138
Cost of 1 pen = Rs \(\\ \frac { 138\times 14 }{ 12 } \)
and cost of 14 pens = Rs 161

Question 13.
Solution:
(b) \(\\ \frac { 24\times 15 }{ 8 } \)
= 45 days

Question 14.
Solution:
(a) \(\\ \frac { 26\times 40 }{ 20 } \)
= 52 men

Question 15.
Solution:
(b) In 6 L of petrol, a car covers = 111 km
In 1 L, it will cover = \(\\ \frac { 111 }{ 6 } \) km
and in 10 L it will cover = \(\\ \frac { 111\times 10 }{ 6 } \) km
= 185 km

Question 16.
Solution:
(a) \(\\ \frac { 28\times 550 }{ 700 } \)
= 22 days

Question 17.
Solution:
Ratio in the angles of triangle
= 3 : 1 : 2

Question 18.
Solution:
(b) Ratio in length and breadth of a rectangle = 5 : 4
Width = 36 m
Length = \(\\ \frac { 5 }{ 4 } \) x 36 m
= 45m

Question 19.
Solution:
Bus covers in 3 hrs = 195 km
It will cover in 1 hr = \(\\ \frac { 195 }{ 3 } \) = 65 km

Question 20.
Solution:
1 dozen = 12 bars
Cost of 5 bars of soap = Rs.82.50

Question 21.
Solution:
Total pencils in 30 packets of 8 pencils
= 30 x 8= 240
and total pencils of 25 packets of 12
pencils = 25 x 12 = 300
Now cost of 240 pencils = Rs. 600
Then cost of 1 percent = Rs. \(\\ \frac { 600 }{ 24 } \)
and cost of 300 pencils = Rs. \(\\ \frac { 600\times 300 }{ 240 } \)
= Rs 750 (b)

Question 22.
Solution:
Journey of 75 km costs = Rs 215
Cost of 1 km = Rs \(\\ \frac { 215 }{ 75 } \)

Question 23.
Solution:
1st term = 12
2nd term = 21
fourth term = 14

Question 24.
Solution:
10 boys dig a patch in = 12 hrs
1 boy will dig it in = 12 x 10 hours

Hope given RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 17 Quadrilaterals Ex 17A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 17 Quadrilaterals Ex 17A

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 17 Quadrilaterals Ex 17A
• RS Aggarwal Solutions Class 6 Chapter 17 Quadrilaterals Ex 17B

Question 1.
Solution:
In the figure, a quadrilateral
(i) Its diagonals are AC and BD
(ii) Two pairs of opposite sides are AB, CD and AD, BC
(iii) Two pairs of opposite angles are ∠A, ∠C and ∠B, ∠D
(iv) Two pairs of adjacent sides are AB, BC and CD and DA
(v) Two pairs of adjacent angles are ∠A, ∠B and ∠B, ∠C

Question 2.
Solution:
Steps of construction :
(i) Draw a line segment AB = 6.5 cm.

(ii) At A, draw a ray AE making an angle of 70° with the help of the protractor and cut off AD = 4.8 cm.
(iii) With centre B and radius 4.8 cm and with centre D and radius 6.5 cm, draw two arcs intersecting each other at C.
(iv) Join BC and DC. Then ABCD is the required parallelogram.
(v) Join AC and BD which measures 9.3 cm and 6.6 cm respectively.

Question 3.
Solution:
Perimeter of the parallelogram = 56 cm
Ratio in sides = 4 : 3
Let first side = 4x
Then second side = 3x
Perimeter = 2 x sum of two sides
=> 56 = 2 x (4x + 3x)
=> 7x × 2 = 56
=> 14x = 56
=> x = \(\\ \frac { 56 }{ 14 } \)
= 4
First side = 4x = 4 × 4 = 16 cm and second side = 3x = 3 × 4 = 12 cm. Ans.

Question 4.
Solution:
(a) A parallelograms whose diagonals are equal and adjacent sides are unequal, is a rectangle.
(b) A parallelogram whose diagonal are equal and also side are equal, is a. square.
(c) A parallelogram whose diagonal are unequal but adjacent sides are equal is a rhombus.

Question 5.
Solution:
A quadrilateral whose one pair of opposite sides are equal but other pair non parallel, is called a trapezium
When the non-parallel sides of a trapezium are equal, then it is called an isosceles trapezium.
ABCD is an isosceles trapezium in which
AD = BC
Then ∠DAB = ∠CBA
On measuring, AD = BC = 3 cm
and ∠DAB = ∠CBA = 60°

Question 6.
Solution:
(a) False , Diagonals of a parallelogram are not equal.
(b) False , Diagonals of a rectangle do not bisect each other at right angles.
(c) False , Diagonals of a rhombus are not equal.

Question 7.
Solution:
(a) Because if each side of a rectangle are equal it is called a square.
(b) Square is a special rhombus if its each angle is equal i.e., of 90°.
(c) If in a parallelogram, if each angle is of 90°, it is called a rectangle.
(d) A square is a parallelogram whose each side and each angle are equal.

Question 8.
Solution:
A regular quadrilateral is a quadrilateral if its each side and angles are equal square is a regular quadrilateral.

 

Hope given RS Aggarwal Solutions Class 6 Chapter 17 Quadrilaterals Ex 17A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10C

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10C.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10A
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10B
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10C
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10D

Question 1.
Solution:
Cost of 14 m of cloth = Rs. 1890
Cost of 1 m = Rs. \(\\ \frac { 1890 }{ 14 } \)
and cost of 6 m = Rs. \(\\ \frac { 1890\times 6 }{ 14 } \)
= Rs. 135 x 6
= Rs. 810

Question 2.
Solution:
Cost of 1 dozen or 12 soaps = Rs. 285.60
Cost of 1 soap = Rs. \(\\ \frac { 285.60 }{ 12 } \)
Cost of 15 soaps = Rs. \(\\ \frac { 285.60\times 15 }{ 12 } \)
= Rs. 357.00

Question 3.
Solution:
Cost of 9 kg of rice = Rs. 327.60
Cost of 1 kg = Rs. \(\\ \frac { 327.60 }{ 9 } \)
and cost of 50 kg = Rs. \(\\ \frac { 327.60\times 50 }{ 9 } \)
= Rs. 36.40 x 50
= Rs. 1820

Question 4.
Solution:
Weight of 22.5 metres of the iron rod: = 85.5 kg
Weight of 1 metre of the iron rod

Question 5.
Solution:
Quantity of oil in 15 tins = 234 kg
Quantity of oil in 1 tin = \(\\ \frac { 234 }{ 15 } \) kg
Quantity of oil in 10 tins

Question 6.
Solution:
Distance covered by the car in 12 litres of diesel = 222 kms
Distance covered by the car in 1 litre of diesel = \(\\ \frac { 222 }{ 12 } \) km

Question 7.
Solution:
Charges of 25 tonnes of weight = Rs. 540
charges of 1 ton = Rs.\(\\ \frac { 540 }{ 25 } \)

Question 8.
Solution:
Weight of copper in 4.5 g of alloy = 3.5g
Weight of copper in 1 g of alloy

Question 9.
Solution:
In Rs. 87.50, the inland letter are purchased = 35
In Re. 1, letters can be purchased
= \(\\ \frac { 35 }{ 87.50 } \)
and in Rs. 315, letters can be purchased

Question 10.
Solution:
4 dozen = 4 x 12 = 48 bananas
In Rs. 104, banana are purchased = 48

Question 11.
Solution:
In Rs. 22770, chairs are purchased =18
In Re. 1, chairs will be purchased
= \(\\ \frac { 18 }{ 22770 } \)
and in Rs. 10120, chairs will be
purchased = \(\\ \frac { 18\times 10120 }{ 22770 } \)
= 8

Question 12.
Solution:
(i) A car travels 195 km distance in = 3 hours
It will travel 1 km distance in = \(\\ \frac { 3 }{ 195 } \) hr.
and it will travel 520 km distance in
= \(\\ \frac { 3\times 520 }{ 195 } \)
= 8 hr
(ii) A car travels in 3hr = 195 km

Question 13.
Solution:
(i) A laborer earn in 12 days = Rs. 1980
He will earn in 1 day = Rs. \(\\ \frac { 1980 }{ 12 } \)
and he will earn in 7 days

Question 14.
Solution:
(i) Weight of 65 books = 13 kg
Then weight of 1 book = \(\\ \frac { 13 }{ 65 } \) kg

Question 15.
Solution:
Number of boxes needed for 6000 pens = 48
Number of boxes needed for 1 pen 48 = \(\\ \frac { 48 }{ 6000 } \)

Question 16.
Solution:
Clearly, less workers will build the wall in more days.
And, more workers will build the wall in less days.
24 workers can build the wall in 15 days
1 worker can build the wall in (15 x 24) days
(less worker, more days)
9 workers will build the wall in

Question 17.
Solution:
Men needed to finish a piece of work in 26 days = 40
Men needed to finish a piece of work in 1 day = 40 x 26 (less days, more men)

Question 18.
Solution:
Clearly, less men will take more days to consume the food.
And, more men will take less days to consume the food.
550 men have provisions for 28 days
1 men has provisions for (28 x 550) days [less men, more days]
700 men will have provisions for

Question 19.
Solution:
Clearly, less persons will consume the rice in more days.
And more persons will consume the rice in less days.
60 persons consume the bag of rice in 3 days.
1 person will consume the bag of rice in
(3 x 60) days (less persons, more days)
18 persons will consume the bag of rice

Hope given RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 16 Triangles Ex 16B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16A
• RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B

Objective questions
Mark against the correct answer in each of following.

Question 1.
Solution:
(c) ∵ It has three sides and three angles i.e. six.

Question 2.
Solution:
(b) ∵ Sum of three angles of a triangle is 180°.

Question 3.
Solution:
(b) ∵ Largest angle
\(=\frac { { 180 }^{ O }\times 4 }{ 2+3+4 } =\frac { { 180 }^{ O }\times 4 }{ 9 } \)
= 80°

Question 4.
Solution:
(d) ∵ A triangle has 180° and if two angles are complementary i.e. sum of two angles is 90°, then third angle will be 180° – 90° = 90°.

Question 5.
Solution:
(c) ∵ Sum of three angles is 180° and sum of two equal angles = 70° + 70° = 140°, then third angle will be 180°- 140° = 40°.

Question 6.
Solution:
(c) ∵ A scalene triangle has different sides.

Question 7.
Solution:
In an isosceles ∆ABC, ∠B = ∠C and bisector of ∠B and ∠C meet at O and ∠A = 40°

Question 8.
Solution:
Side of a triangle are in the ratio 3:2:5 and perimeter = 30 m
Length of longest side = \(\frac { 30\times 5 }{ 3+2+5 } \)
= \(\frac { 30\times 5 }{ 10 } \) cm
= 15 cm (b)

Question 9.
Solution:
Two angles of a triangle are 30° and 25° But sum of three angles of a triangle – 180°
Third angle = 180° – (30 + 25°)
= 180° – 55° = 125° (d)

Question 10.
Solution:
Each angles of an equilateral triangle = 60°
as each angle of an equilateral triangle are equal
Each angle = \(\\ \frac { 180 }{ 3 } \) = 60° (c)

Question 11.
Solution:
In the figure, P lies on AB
Its lies on the ∆ABC (c)

Hope given RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 10 Ratio, Proportion and Unitary Method Ex 10B

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10B.

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10A
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10B
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10C
• RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10D

Question 1.
Solution:
(i) 4, 6, 8, 12
If it is in proportion, then
If ad = bc if 4 x 12 = 6 x 8
If 48 = 48
Which is true
∴ 4, 6, 8, 12 are in proportion
(ii) 7, 42, 13, 78
7 : 42 :: 13 : 78
If ad = bc if 7 x 78 = 42 x 13
If 546 = 546
Which is true
∴ 7, 42, 13, 78 are in proportion
(iii) 33, 121, 9, 96 or 33 : 121 :: 9 : 96
are in proportion
If ad = bc
If 33 x 96 = 121 x 9
If 3168 = 1089
Which is not true
∴ 33, 121,9, 96 are not in proportion
(iv) 22, 33, 42, 63 or 22 : 33 :: 42 : 63
are in proportion
If ad = bc
If 22 x 63 = 33 x 42
If 1386 = 1386
Which is true
∴ 22, 33, 42, 63 are in proportion
(v) 32, 48, 70, 210 or 32 : 48 :: 70 : 210
are in proportion
If ad = bc
If 32 x 210 = 48 x 70
If 6720 = 3360
Which is not true
∴ 32, 48, 70, 210 are not in proportion
(vi) 150, 200, 250, 300 or
150 : 200 :: 250 : 300 are in proportion
If ad = bc if 150 x 300 = 200 x 250
If 45000 = 50000
Which is not true
∴ 150, 200,250, 300 are not in proportion

Question 2.
Solution:
(i) We have 60 : 105 :: 84 : 147
Product of means = 105 x 84 = 8820
Product of extremes = 60 x 147 = 8820
∴ Product of means = Product of extremes
Hence 60 : 105 :: 84 : 147 is verified.
(ii) We have 91 : 104 :: 119 : 136
Product of means = 104 x 119 = 12376
Product of extremes = 91 x 136 = 12376
Product of means = Product of extremes
Hence 91 : 104 :: 119 : 136 is verified.
(iii) We have 108 : 72 :: 129 : 86
Product of means = 72 x 129 = 9288
Product of extremes = 108 x 86 = 9288
Product of means = Product of extremes
Hence 108 : 72 :: 129 : 86 is verified.
(iv) We have 39 : 65 :: 141 : 235
Product of means = 65 x 141 = 9165
Product of extremes = 39 x 235 = 9165
∴ Product of means = Product of extremes
Hence 39 : 65 :: 141 : 235 is verified.

Question 3.
Solution:
(i) We have 55 : 11 :: x : 6
Product of means = 11 × x = 11x
Product of extremes = 55 x 6 = 330

Question 4.
Solution:
(i) We have, 51 : 68 = \(\\ \frac { 51 }{ 68 } \)
= \(\\ \frac { 3 }{ 4 } \)

Question 5.
Solution:
(i) 25 cm : 1 m and Rs. 40 : Rs. 160
= \(\\ \frac { 25cm }{ 1000cm } \) = \(\\ \frac { 1 }{ 4 } \),
\(\\ \frac { Rs.40 }{ Rs.160 } \) = \(\\ \frac { 1 }{ 4 } \)

Question 6.
Solution:
Let the third term be x.
Then 51 : 68 :: x : 108
Now, product of means = x × 68
And, product of extremes = 51 × 108
x × 68 = 51 × 108
=> x = \(\\ \frac { 51\times 108 }{ 68 } \)
= 3 × 27 = 81
x = 81
Hence the third term of the given proportion is 81

Question 7.
Solution:
1st term =12, third term = 8 and fourth term = 14
Let 2nd term = x, then

Question 8.
Solution:
(i) The given numbers 48, 60, 75 are in
continued proportion if 48 : 60 :: 60 : 75.
Now, product of means = 60 x 60 = 3600
And, product of extremes = 48 x 75 = 3600
∴ Product of means = Product of extremes
So, 48 : 60 :: 60 : 75
Hence, the numbers 48, 60, 75 are in continued proportion.
(ii) The given numbers 36, 90, 225 are in
continued proportion of 36 : 90 :: 90 : 225
Now, product of means = 90 x 90 = 8100
And, product of extremes = 36 x 225 = 8100
∴ Product of means = Product of extremes
So, 36 : 90 :: 90 : 225
Hence, the numbers 36, 90, 225 are in continued proportion.
(iii)The given numbers 16, 84, 441 are in
continued proportion if 16 : 84 :: 84 : 441.
Now, product of means = 84 x 84 = 7056
And, product of extremes = 16 x 441 = 7056
Product of means = Product of extremes.
So, 16 : 845 :: 84 : 441
Hence 16, 84, 441 are in continued proportion.
(iv) The given numbers 27, 36, 48 are
in continued proportion if 27 : 36 :: 36 : 48
Now, product of means = 36 x 36 = 1296
And, product of extremes = 27 x 48 = 1296
∴ Product of means = Product of extremes.
So, 27 : 36 :: 36 : 48
Hence, the numbers 27, 36, 48 are in continued proportional.

Question 9.
Solution:
It is given that 9, x, x, 49 are in proportion, that is, 9 : x :: x : 49
∴ Product of means = Product of extremes

Question 10.
Solution:
Let the height of the pole be x metres.

Question 11.
Solution:
5 : 3 :: x : 6

Hope given RS Aggarwal Solutions Class 6 Chapter 10 Ratio, Proportion and Unitary Method Ex 10B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 16 Triangles Ex 16A

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16A

Other Exercises

• RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16A
• RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16B

Question 1.
Solution:
A, B and C are three non-collinear points in a plane. AB, BC and CA are joined.

(i) The side opposite ∠C is AB
(ii) The angle opposite to the side BC is ∠A
(iii) The vertex opposite to the side CA is B
(iv) The side opposite to the vertex B is CA

Question 2.
Solution:
The measures of two angles of a triangle are 72° and 58°
But measure of three angles of a triangle is 180°
Third angle will be = 180 – (72° + 58°)
= 180° – 130°
= 50°

Question 3.
Solution:
Sum of three angles of a triangle = 180°
Ratio of three angles = 1 : 3 : 5

Hence, three angles are 20°, 60° and 100°
Ans.

Question 4.
Solution:
Sum of three angles of a right triangle = 180°
Sum of two acute angles = 180°- 90°
= 90°
Measure of one angle = 50°
Second acute angle = 90° – 50° = 40°
Ans.

Question 5.
Solution:
Let the measure of each of the equal angles be x°. Then,
x° + x°+ 110°= 180°
(Angle sum property of a triangle)
=> 2x°+110°= 180°
=> 2x° = 180° – 110° = 70°
=> \({ x }^{ O }={ \left( \frac { 70 }{ 2 } \right) }^{ O }={ 35 }^{ O }\)
The measure of each of the equal angles is 35°.

Question 6.
Solution:
Let the three angles of a triangle be ∠A, ∠B, ∠C. Then, ∠A = ∠B + ∠C
Adding ∠A to both sides, we get ∠A + ∠A = ∠A + ∠B + ∠C
=> 2 ∠A = 180°
(Angle sum property of a triangle)
=> ∠A = \({ \left( \frac { 180 }{ 2 } \right) }^{ O }={ 90 }^{ O }\)
One of the angles of the triangle is a right angle.
Hence, the triangle is a right triangle

Question 7.
Solution:
In a ∆ABC,
3∠A = 4∠B = 6∠C = 1 (say)

Question 8.
Solution:
(i) It is obtuse triangle.
(ii) It is acute triangle.
(iii) It is right triangle.
(iv) It is obtuse triangle.

Question 9.
Solution:
(i) It is an isosceles triangle as it has two equal sides.
(ii) It is an isosceles triangle as it has two equal sides.
(iii) It is a scalene triangle as its sides are different in length.
(iv) It is an equilateral triangle as its all sides are equal.
(v) It is an equilateral triangles as its angles are equal, so its sides will also be equal.
(vi) It is an isosceles triangle as its two base angles are equal, so its two sides are equal.
(vii) It is a scalene triangle as its angles are different, so its sides will also be different or unequal.

Question 10.
Solution:
In ∆ABC, D is a point on BC and AD is joined
Now we get triangles ∆ABC, ∆ABD and ∆ADC

Question 11.
Solution:
(i) No
(ii) No
(iii) Yes
(iv) No
(v) No
(vi) Yes.

Question 12.
Solution:
(i) three, three, three.
(ii) 180°
(iii) different
(iv) 60°
(v) equal
(vi) perimeter.

 

Hope given RS Aggarwal Solutions Class 6 Chapter 16 Triangles Ex 16A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

RS Aggarwal Class 6 Solutions Chapter 15 Polygons Ex 15

These Solutions are part of RS Aggarwal Solutions Class 6. Here we have given RS Aggarwal Solutions Class 6 Chapter 15 Polygons Ex 15

Question 1.
Solution:
(a), (b), (d) and (f) are simple closed figures.

Question 2.
Solution:
(a), (b) and (c) are polygons.

Question 3.
Solution:
(i) two
(ii) triangle
(iii) quadrilateral
(iv) 3, 3
(v) 4, 4
(vi) closed figure.

 

Hope given RS Aggarwal Solutions Class 6 Chapter 15 Polygons Ex 15 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.