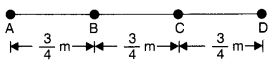
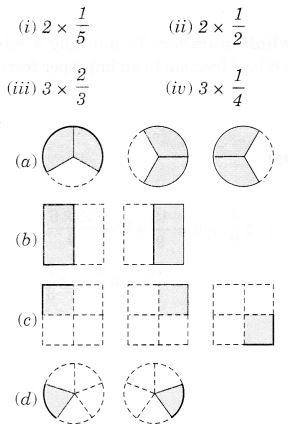
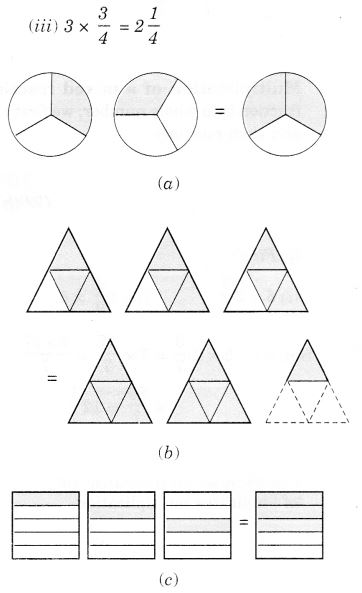
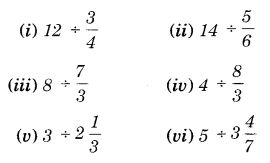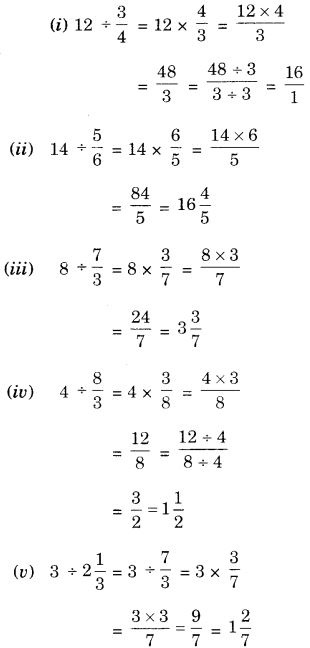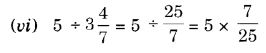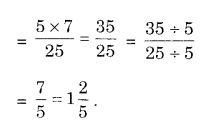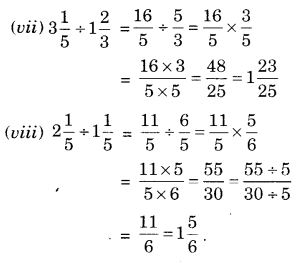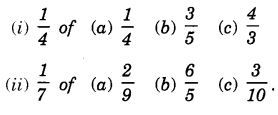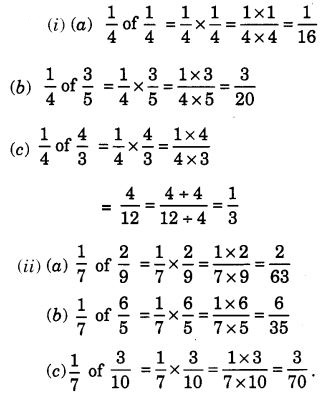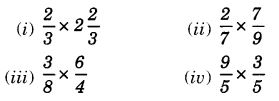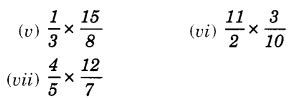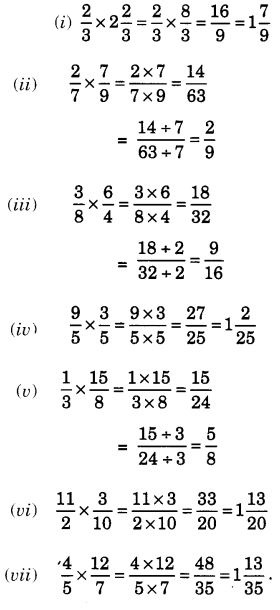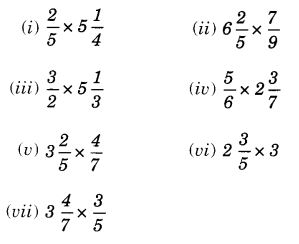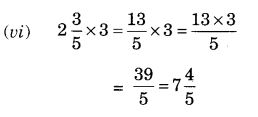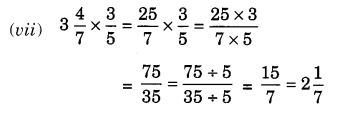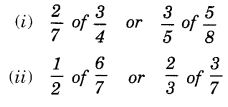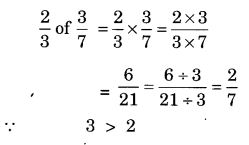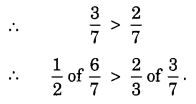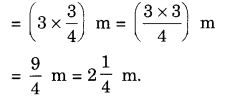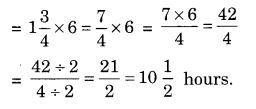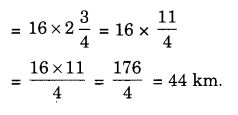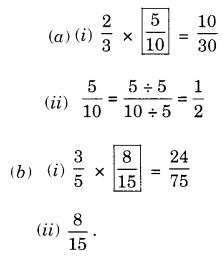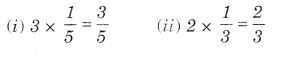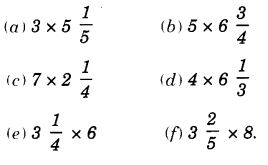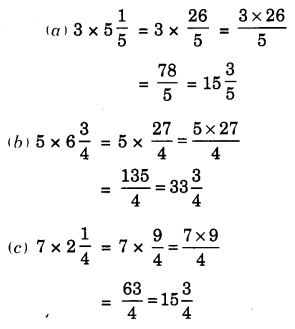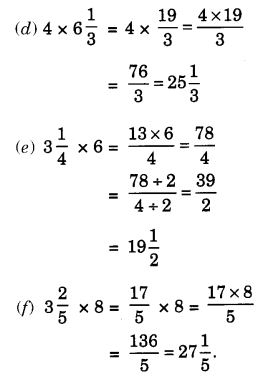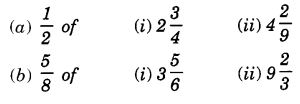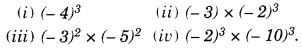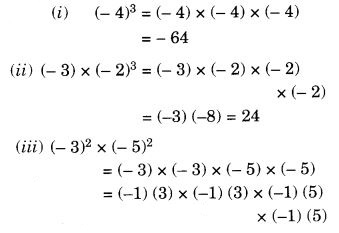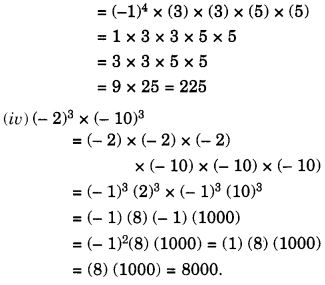NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.5 are part of NCERT Solutions for Class 7 Maths. Here we have given NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.5.
- Fractions and Decimals Class 7 Ex 2.1
- Fractions and Decimals Class 7 Ex 2.2
- Fractions and Decimals Class 7 Ex 2.3
- Fractions and Decimals Class 7 Ex 2.4
- Fractions and Decimals Class 7 Ex 2.6
- Fractions and Decimals Class 7 Ex 2.7
- Fractions and Decimals Class 7 MCQ
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 7 |
| Subject | Maths |
| Chapter | Chapter 2 |
| Chapter Name | Fractions and Decimals |
| Exercise | Ex 2.5 |
| Number of Questions Solved | 9 |
| Category | NCERT Solutions |
NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.5
Question 1.
Which is greater?
- 0.5 or 0.05
- 0.7 or 0.5
- 7 or 0.7
- 1.37 or 1.49
- 2.03 or 2.30
- 0.8 or 0.88
Solution:

Question 2.
Express as rupees using decimals:
- 7 paise
- 7 rupees 7 paise
- 77 rupees 77 paise
- 50 paise
- 235 paise.
Solution:
- 7 paise = ₹ 0.07
- 7 rupees 7 paise = ₹ 7.07
- 77 rupees 77 paise = ₹ 77.77
- 50 paise – ₹ 0.50
- 235 paise = ₹ 2.35
Question 3.
- Express 5 cm in metre and kilometre
- Express 35 mm in cm, m and km?
Solution:
- 5 cm = 0.05 m = 0.00005 km
- 35 mm = 3.5 cm = 0.035 m = 0.000035 km
Question 4.
Express in kg:
- 200 g
- 3470 g
- 4 kg 8 g
Solution:
- 200 g = 0.200 kg = 0.2 kg
- 3470 g = 3.470 kg
- 4 kg 8 g = 4.008 kg.
Question 5.
Write the following decimal numbers in the expanded form:
- 20.03
- 2.03
- 200.03
- 2.034
Solution:
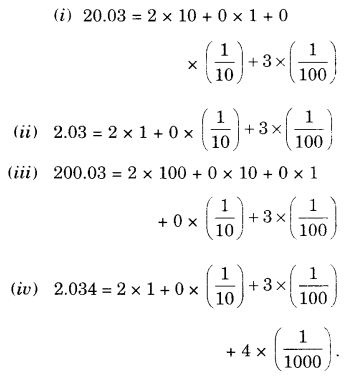
Question 6.
Write the place value of 2 in the following decimal numbers:
- 2.56
- 21.37
- 10.25
- 9.42
- 63.352
Solution:
(i) Place value of 2 in the decimal number 2.56 = 2 × 1 = 2
(ii) Place value of 2 in decimal number 21.37 = 2 × 10 = 20
(iii) Place value of 2 in the decimal number

Question 7.
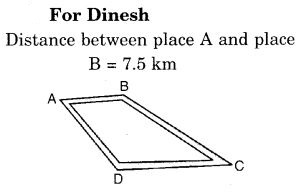
Dinesh went from place A to place t B and from there to place C. A is 7.5 km from B and B is 12.7 km from C. Ayub went from place A to place D and from there to place C. D is 9.3 km from A and C is 11.8 km from D. f Who travelled more and by how much?
Solution:


Question 8.
Shyama bought 5 kg 300 g apples and 3 kg 250 g mangoes. Sarala bought 4 kg 800 g oranges and 4 kg 150 g bananas. Who bought more fruits?
Solution:
For Shyama
Apples bought = 5 kg 300 g = 5.300 kg
Mangoes bought = 3 kg 250 g = 3.250 kg
∴ Fruits bought = Apples bought
+ Mangoes bought = 5.300 kg + 3.250 kg

For Sarala
Oranges bought = 4 kg 800 g = 4.800 kg
Bananas bought = 4 kg 150 g = 4.150 kg
∴ Fruits bought = Oranges bought
+ Bananas bought
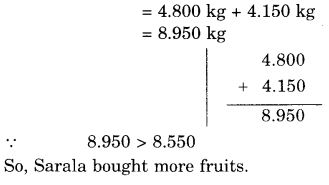
Question 9.
How much less is 28 km than 42.6 km?
Solution:
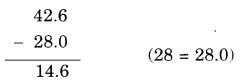
So, 28 km is less than 42.6 km by 14.6 km.
We hope the NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.5 help you. If you have any query regarding NCERT Solutions for Class 7 Maths Chapter 2 Fractions and Decimals Ex 2.5, drop a comment below and we will get back to you at the earliest.