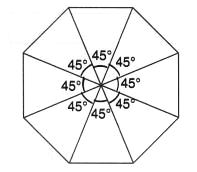
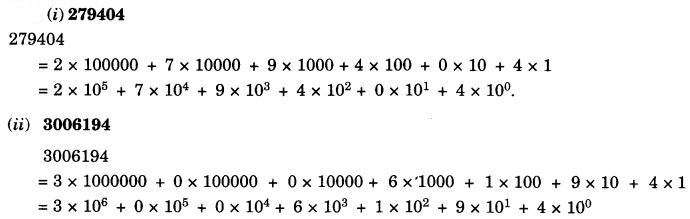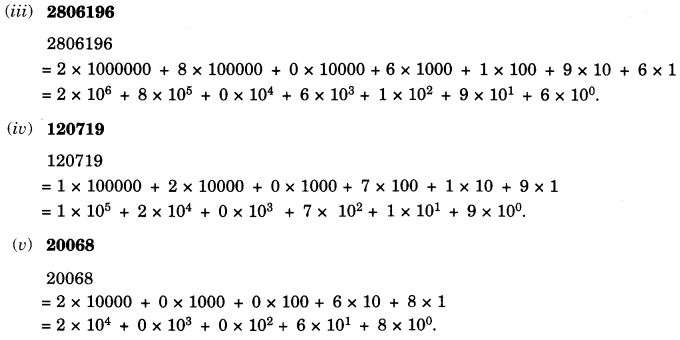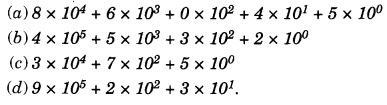On this page, you will find Nutrition in Plants Class 7 Notes Science Chapter 1 Pdf free download. CBSE NCERT Class 7 Science Notes Chapter 1 Nutrition in Plants will seemingly help them to revise the important concepts in less time.
CBSE Class 7 Science Chapter 1 Notes Nutrition in Plants
Nutrition in Plants Class 7 Notes Understanding the Lesson
1. Vitamins, carbohydrates, proteins, fats and minerals are the components of food. These components of food are necessary for our body and are called nutrients.
2. The process of procuring and utilization of food by the body is called nutrition.
3. The mode of nutrition in which organisms make food themselves from simple substances is called autotrophic nutrition.
4. The organisms which cannot make their food and depend on others for their food are called heterotrophs and this type of nutrition is called heterotrophic nutrition.
5. Carbon dioxide from air is taken in through the tiny pores present on the surface of the leaves. These pores are surrounded by ‘guard cells’ such pores are called stomata.
6. The leaves have a green pigment and they are known as chlorophyll.
7. Plants use sunlight, carbon dioxide and water in presence of chlorophyll to synthesise their food. This process is known as photosynthesis.
![]()
8. The sun is the ultimate source of energy for all living organisms.
9. The bodies of living organisms are made of tiny units which are called cells.
10. The organisms either plants or animals that derive nutrients from another organisms are known as parasites. For example, Cuscuta, lice, etc.
11. The organisms which provide nutrients to another organisms without being benefitted are known as hosts.
12. The type of plants which trap insects and digest them by producing digestive juices are called insectivorous plants. For example, pitcher plant, sundew, venus fly trap, etc.
13. The mode of nutrition in which organisms take in nutrients in form of solution from dead and decaying matter is called saprophytic nutrition.
14. Plants which use saprophytic mode of nutrition are called saprotrophs.
15. The organisms which live together and share shelter and nutrients are said to be in symbiotic relationship. For example, certain fungi live in the roots of trees.
Class 7 Science Chapter 1 Notes Important Terms
Autotrophic: It is the mode of nutrition in which organisms prepare its own food by using sunlight, air and other essential substances.
Chlorophyll: Chlorophyll is a green pigment present in leaves which absorb solar energy from sunlight, and enables the plant to prepare their food through the process of photosynthesis.
Heterotrophs: The organisms which cannot prepare their food and depends on other organisms for their food are known as heterotrophs.
Host: A plant or an animal which support other organisms by giving food, shelter, etc., is known as host.
Insectivorous: The plant or animal which eat insect for their survival is known as insectivorous.
Nutrients: Vitamins, carbohydrates, proteins, fats and minerals are the components of food. These components of food are essential for our body and are called nutrients.
Parasite: The organism which depends on other organisms for deriving nutrients and their survival is known as parasite.
Photosynthesis: The process by which plants prepare their own food in the presence of sunlight, water, carbon dioxide and chlorophyll is called photosynthesis.
Saprotrophs: Organisms which take their nutrients from dead and decaying matter are called saprotrophs.
Saprotrophic: The mode of nutrition in which an organism take its food from dead and decaying matter is known as saprotrophic mode of nutrition.
Stomata: The tiny pores which are present on the surface of the leaves are called stomata.