Category: CBSE Class 8

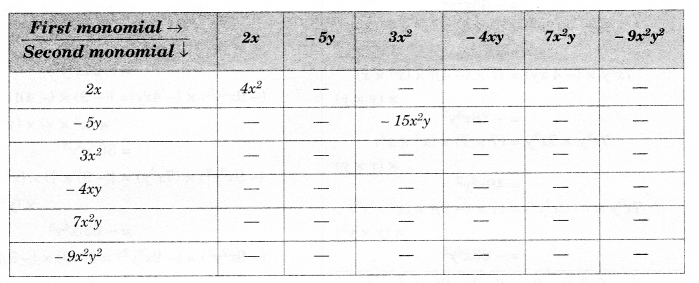
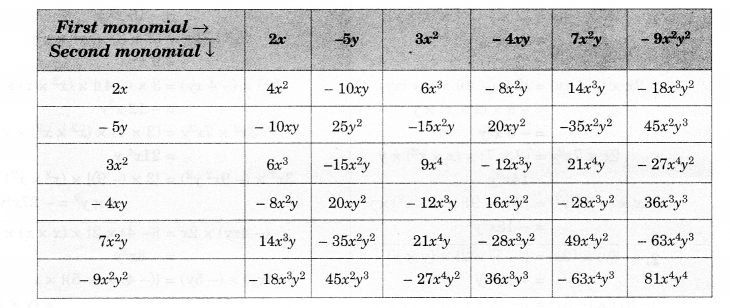
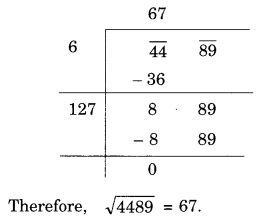
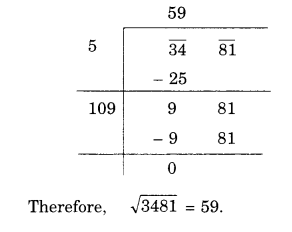
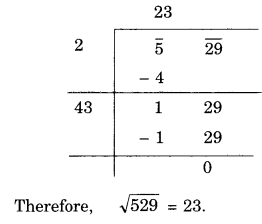
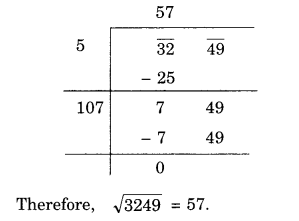
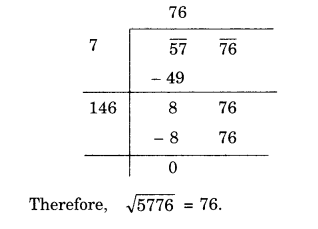
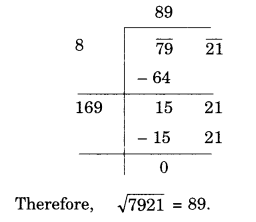
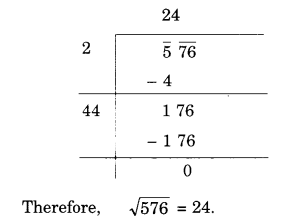
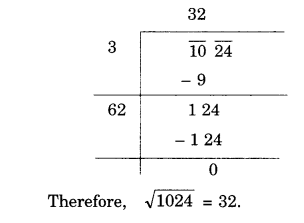
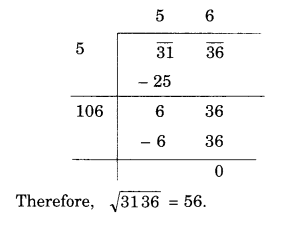
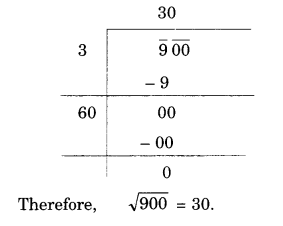
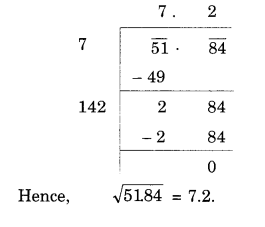
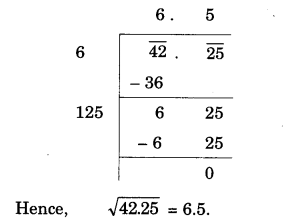
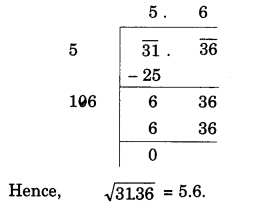
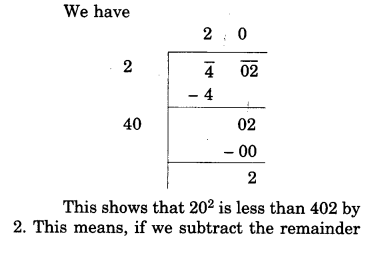
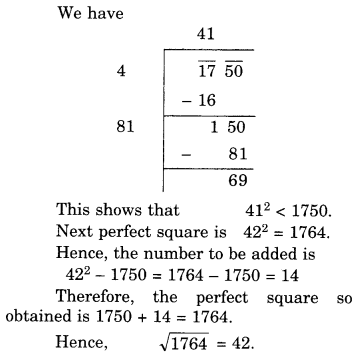
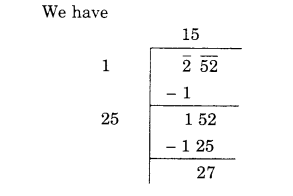
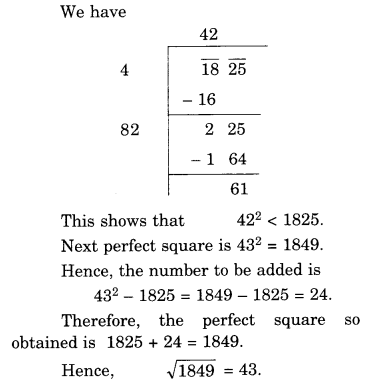
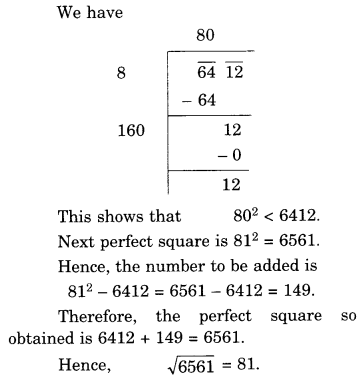
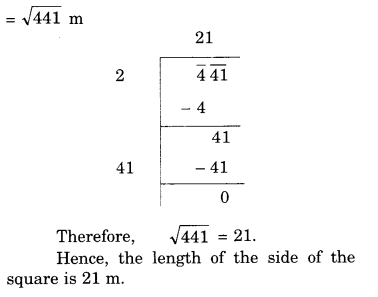
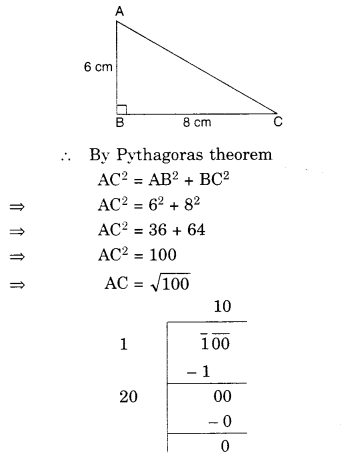
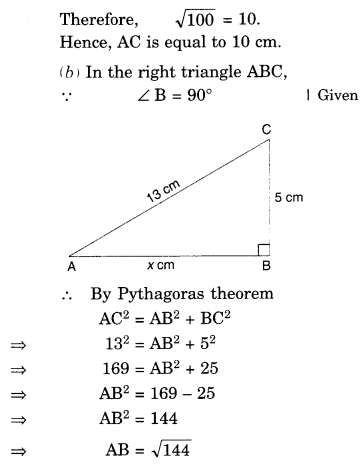
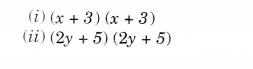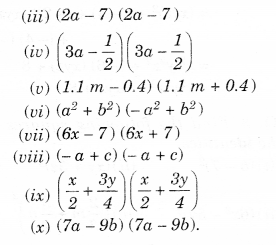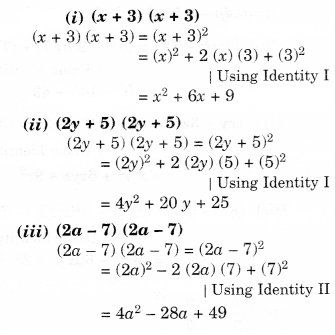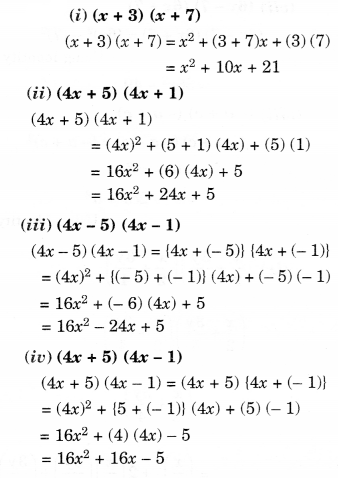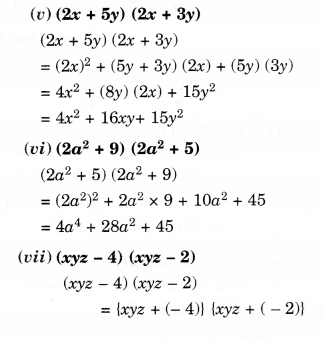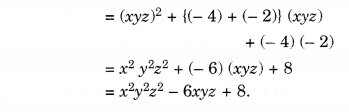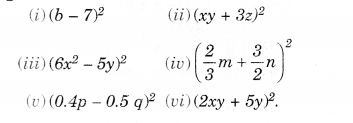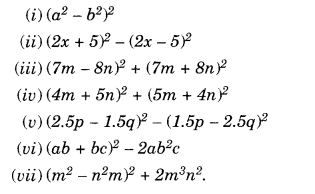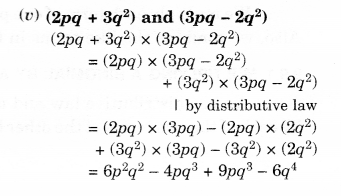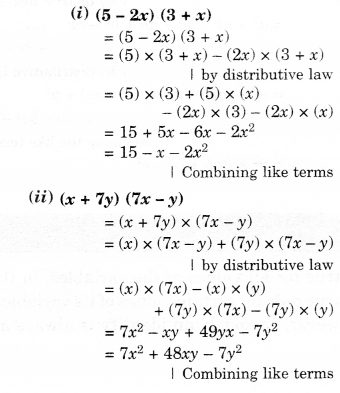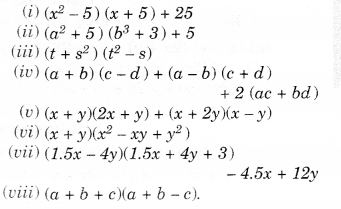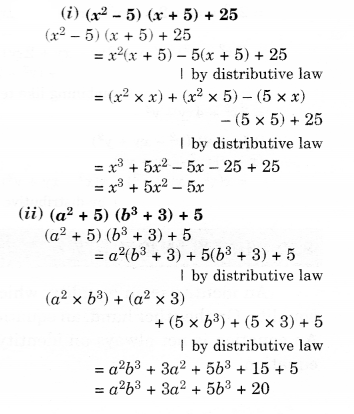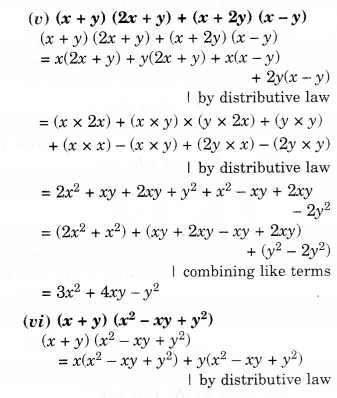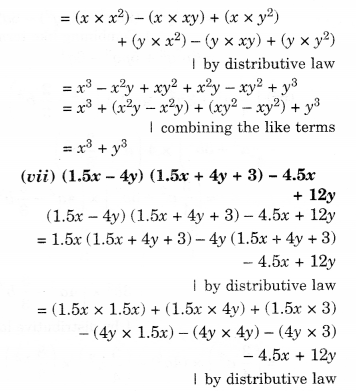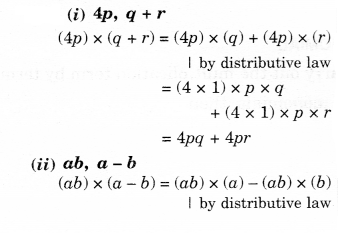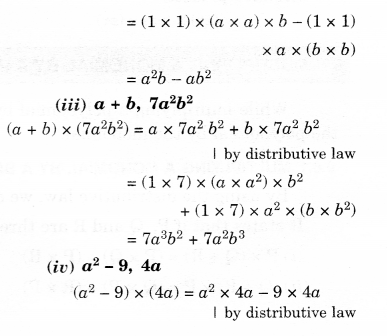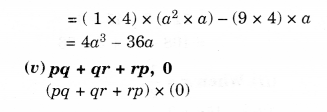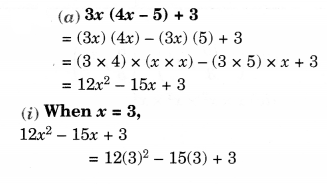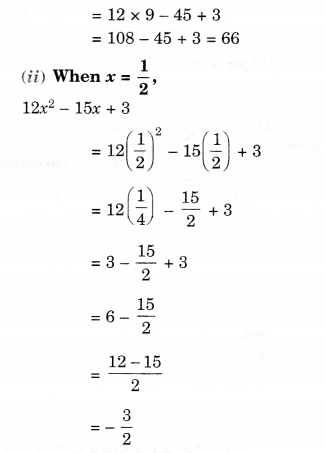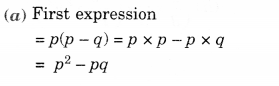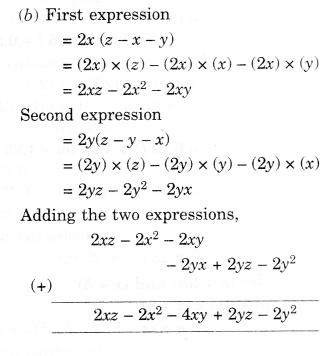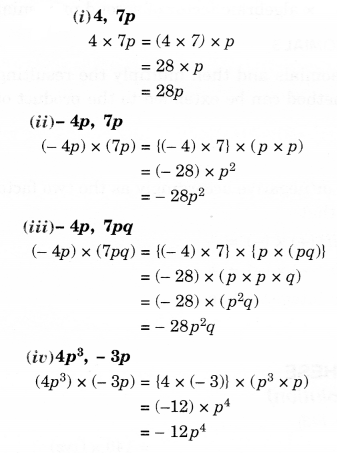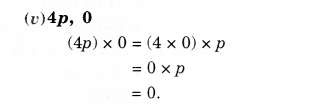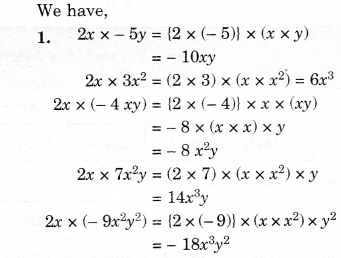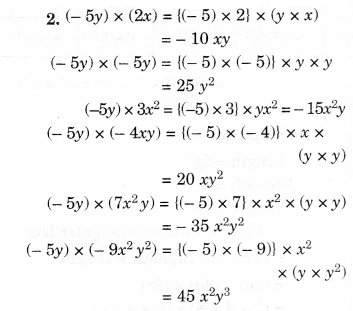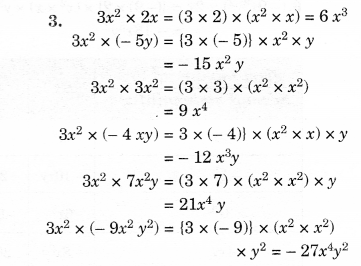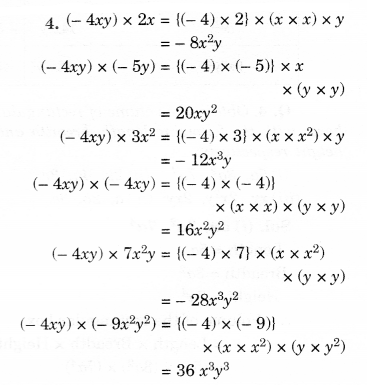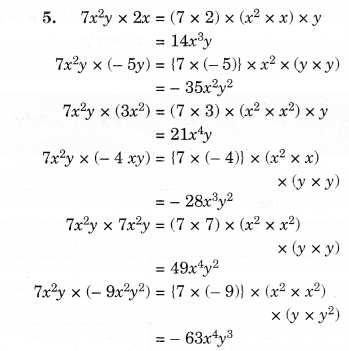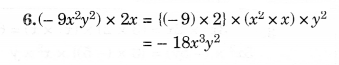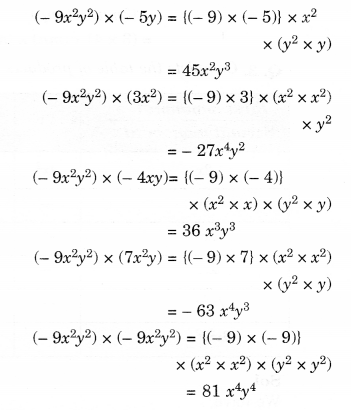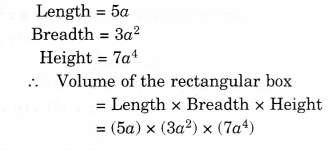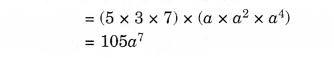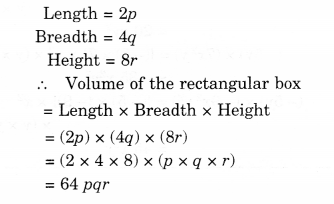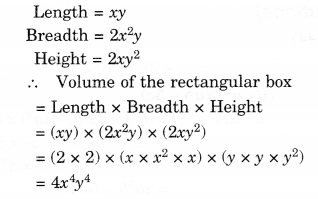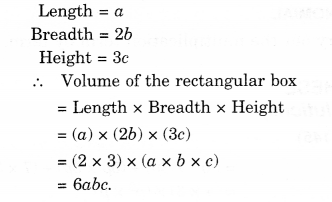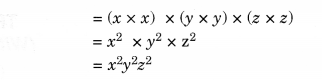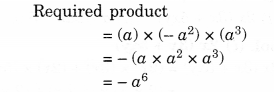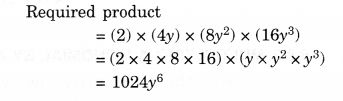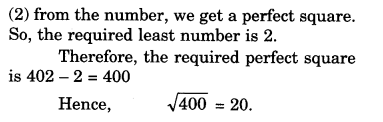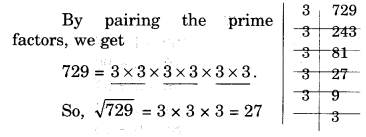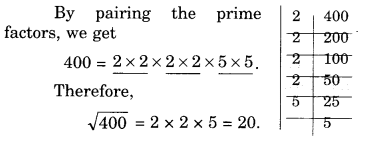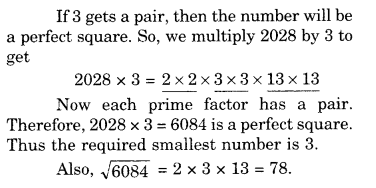NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.2.

• Visualising Solid Shapes Class 8 Ex 10.1
• Visualising Solid Shapes Class 8 Ex 10.3

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 10
Chapter Name	Visualising Solid Shapes
Exercise	Ex 10.2
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.2

Question 1.
Look at the given map of a city.
Answer the following.
(a) Colour the map as follows: Bluewater, Red-fire station, Orange-Library, Yellow-schools, Green-Parks, Pink-Community Centre, Purple-Hospital, Brown-Cemetery.
(b) Mark a green X’ at the intersection of Road ‘C’ and Nehru Road, Green Y’ at the intersection of Gandhi Road and Road A.
(c) In red, draw a short street route from Library to the bus depot.
(d) Which is further east, the city park or the market?
(e) Which is further south, the primary school or the Sr. Secondary School?

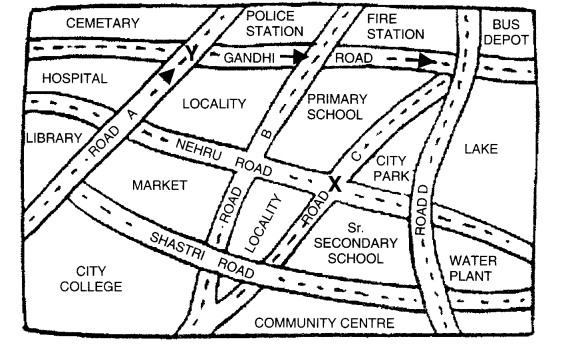
Solution.
(a) Please color yourself.
(b) See the above figure.
(c) See the above figure.
(d) City Park.
(e) Senior Secondary school.

Question 2.
Draw a map of your classroom using a proper scale and symbols for different objects.
Solution.
Please draw yourself.

Question 3.
Draw a map of your school compound using a proper scale and symbols for various features like playground main building, garden etc.
Solution.
Please draw yourself.

Question 4.
Draw a map giving instructions to your friend so that she reaches your house without any difficulty.
Solution.
Please draw yourself.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.2 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 10 Visualising Solid Shapes Ex 10.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5.

• Algebraic Expressions and Identities Class 8 Ex 9.1
• Algebraic Expressions and Identities Class 8 Ex 9.2
• Algebraic Expressions and Identities Class 8 Ex 9.3
• Algebraic Expressions and Identities Class 8 Ex 9.4

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 9
Chapter Name	Algebraic Expressions and Identities
Exercise	Ex 9.5
Number of Questions Solved	8
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5

Question 1.
Use a suitable identity to get each of the following products:


Solution.

Question 2.
Use the identity \((x+a)(x+b)={ x }^{ 2 }+(a+b)x+ab\) to find the following products:
(i) (x + 3) (x + 7)
(ii) (4x + 5) (4x + 1)
(iii) (4x – 5) (4x – 1)
(iv) (4x + 5) (4x – 1)
(v) (2x + 5y) (2x + 3y)
(vi) \((2{ a }^{ 2 }+9)(2{ a }^{ 2 }+5)\)
(vii) (xyz – 4) (xyz – 2).
Solution.

Question 3.
Find the following squares by using the identities.

Solution.

Question 4.
Simplify:

Solution.

Question 5.
Show that:

Solution.

Question 6.
Using identities, evaluate:

Solution.

Question 7.
Using \({ a }^{ 2 }-{ b }^{ 2 }=(a+b)(a-b)\), find

Solution.

Question 8.
Using \((x+a)(x+b)={ x }^{ 2 }+(a+b)x+ab\), find
(i) 103 x 104
(ii) 5.1 x 5.2
(iii) 103 x 98
(iv) 9.7 x 9.8
Solution.

We hope the NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.5, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4.

• Algebraic Expressions and Identities Class 8 Ex 9.1
• Algebraic Expressions and Identities Class 8 Ex 9.2
• Algebraic Expressions and Identities Class 8 Ex 9.3
• Algebraic Expressions and Identities Class 8 Ex 9.5

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 9
Chapter Name	Algebraic Expressions and Identities
Exercise	Ex 9.4
Number of Questions Solved	3
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4

Question 1.
Multiply the binomials:
(i) (2x + 5) and (4x – 3)
(ii) (y – 8) and (3y – 4)
(iii) (2.5l – 0.5 m) and (2.5l + 0.5m)
(iv) (a + 3b) and (x + 5)
(v) \((2pq+3{ q }^{ 2 })\quad and\quad (3pq-2{ q }^{ 2 })\)
(vi) \((\frac { 3 }{ 4 } { a }^{ 2 }+3{ b }^{ 2 })\quad and\quad 4({ a }^{ 2 }-\frac { 2 }{ 3 } { b }^{ 2 })\)
Solution.

Question 2.
Find the product:
(i) (5 – 2x) (3 + x)
(ii) (x + 7y) (7x —y)
(iii) \(({ a }^{ 2 }+b)(a+{ b }^{ 2 })\)
(iv) \(({ p }^{ 2 }-{ q }^{ 2 })(2p+q)\)
Solution.

Question 3.
Simplify.

Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.4, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.3 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.3.

• Algebraic Expressions and Identities Class 8 Ex 9.1
• Algebraic Expressions and Identities Class 8 Ex 9.2
• Algebraic Expressions and Identities Class 8 Ex 9.4
• Algebraic Expressions and Identities Class 8 Ex 9.5

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 9
Chapter Name	Algebraic Expressions and Identities
Exercise	Ex 9.3
Number of Questions Solved	5
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.3

Question 1.
Carry out the multiplication of the expressions in each of the following pairs:
(i) 4p, q + r
(ii) ab, a – b
(iii) \(a+b,\quad 7{ a }^{ 2 }{ b }^{ 2 }\)
(iv) \({ a }^{ 2 }-9,\quad 4a\)
(v) pq + qr + rp, 0
Solution.

Question 2.
Complete the table

Solution.

Question 3.
Find the product:


Solution.

Question 4.
(a) Simplify: 3x (4x – 5) + 3 and find its values for (i) x = 3, (ii) \(x=\frac { 1 }{ 2 } \)
(b) Simplify: \(a({ a }^{ 2 }+a+1)+5\) and find its value for (i)a = 0, (ii)a = 1 and (iii) a = -1.
Solution.

Question 5.
(a) Add: p(p – q), q(q – r) and r(r -p)
(b) Add: 2x(z – x – y) and 2y (z – y – x)
(c) Subtract: 3l (l – 4m + 5n) from 4l (10n – 3m + 2l)
(d) Subtract: 3a(a + b + c) – 2b(a – b + c) from 4c(- a + b + c).
Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.3 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.3, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.2.

• Algebraic Expressions and Identities Class 8 Ex 9.1
• Algebraic Expressions and Identities Class 8 Ex 9.3
• Algebraic Expressions and Identities Class 8 Ex 9.4
• Algebraic Expressions and Identities Class 8 Ex 9.5

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 9
Chapter Name	Algebraic Expressions and Identities
Exercise	Ex 9.2
Number of Questions Solved	5
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.2

Question 1.
Find the product of the following pairs of monomials:
(i) 4, 7p
(ii) – 4p, 7p
(iii) – 4p, 7pq
(iv) \(4{ p }^{ 3, },\quad -3p\)
(v) 4p, 0.
Solution.

Question 2.
Find the areas of rectangles with the following pairs of mononials as their lengths and breadths respectively:
(i) (p, q);
(ii) (10m, 5n);
(iii) (\(20{ x }^{ 2 },\quad 5{ y }^{ 2 }\));
(iv) (\(4x,\quad 3{ x }^{ 2 }\));
(v) (3mn, 4np).
Solution.
(i) (p, q)
Length = p
Breadth = q
∴ Area of the rectangle
= Length x Breadth
= pxq
= pq

(ii) (10m, 5n)
Length = 10 m
Breadth = 5 n
∴ Area of the rectangle
= Length x Breadth
= (10m) x (5n)
= (10 x 5) x (m x n)
= 50 x (mn)
= 50 mn

(iii) (\(20{ x }^{ 2 },\quad 5{ y }^{ 2 }\))
Length = \(20{ x }^{ 2 }\)
Breadth = \(5{ y }^{ 2 }\)
∴ Area of the rectangle
= Length x Breadth
= (\(20{ x }^{ 2 }\)) x (\(5{ y }^{ 2 }\))
= (20 x 5) x (\({ x }^{ 2 }\times { y }^{ 2 }\))
= 100 x (\({ x }^{ 2 }{ y }^{ 2 }\))
= 100\({ x }^{ 2 }{ y }^{ 2 }\)

(iv) (4x, 3xP)
Length = 4.x
Breadth = \(3{ x }^{ 2 }\)
∴ Area of the rectangle
= Length x Breadth =
(4x) x (\(3{ x }^{ 2 }\))
= (4 x 3) x (\(x\times { x }^{ 2 }\))
= 12 x \({ x }^{ 3 }\)
= 12×3

(v) (3mn, 4np)
Length = 3 mn
Breadth = 4np
∴ Area of the rectangle
= Length x Breadth
= (3mn) x (4np)
= (3 x 4) x (mn) x (np)
= 12 x m x (n x n) x p
= 12\(m{ n }^{ 2 }p\)

Question 3.
Complete the table of products.

Solution.

Question 4.
Obtain the volume of rectangular boxes with the following length, breadth and height respectively:
(i) \(5a,\quad 3{ a }^{ 2 },\quad 7{ a }^{ 4 }\)
(ii) 2p, 4q, 8r
(iii) \(xy,\quad 2{ x }^{ 2 }y,\quad 2x{ y }^{ 2 }\)
(iv) a, 2b, 3c
Solution.
(i) \(5a,\quad 3{ a }^{ 2 },\quad 7{ a }^{ 4 }\)

(ii) 2p, 4q, 8r

(iii) \(xy,\quad 2{ x }^{ 2 }y,\quad 2x{ y }^{ 2 }\)

(iv) a, 2b, 3c

Question 5.
Obtain the product of
(i) xy, yz, zx
(ii) \(a,\quad -{ a }^{ 2 },\quad { a }^{ 3 }\)
(iii) \(2,\quad 4y,\quad 8{ y }^{ 2 },\quad 16{ y }^{ 3 }\)
(iv) a, 2b, 3c, 6abc
(v) m, – mn, mnp.
Solution.
(i) xy, yz, zx
Required product
= (xy) x (yz) x (zx)

(ii) \(a,\quad -{ a }^{ 2 },\quad { a }^{ 3 }\)

(iii) \(2,\quad 4y,\quad 8{ y }^{ 2 },\quad 16{ y }^{ 3 }\)

(iv) a, 2b, 3c, 6abc

(v) m, – mn, mnp.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.2 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 9 Algebraic Expressions and Identities Ex 9.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.2.

• Comparing Quantities Class 8 Ex 8.1
• Comparing Quantities Class 8 Ex 8.3

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 8
Chapter Name	Comparing Quantities
Exercise	Ex 8.2
Number of Questions Solved	10
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.2

Question 1.
A man got a 10% increase in his salary. If his new salary is f1,54,000, find his original salary.
Solution.
100 + 10 = 110

Question 2.
On Sunday 845 people went to the Zoo. On Monday only 169 people went. What is the percent decrease in the people visiting the Zoo on Monday?
Solution.
Number of people who went to Zoo on Sunday = 845
Number of people who went to Zoo on Monday = 169
∴ Decrease in the number of people who went to Zoo 845 – 169 = 676.
∴Per cent decrease in the number of people visiting the Zoo on Monday
= \(\frac { decrease }{ original\quad number } \times 100%\)
= \(\frac { 676 }{ 845 } \times 100%=80%\)

Question 3.
A shopkeeper buys 80 articles for ₹ 2,400 and sells them for a profit of 16%. Find the selling price of one article.
Solution.
CP of 80 articles = ₹ 2400
Profit = 16% of ₹ 2400
= ₹ \(\frac { 16 }{ 100 } \times 2400\) = ₹ 384
∴SP of 80 articles
= CP + Profit
= ₹ 2400 + ₹ 384
= ₹ 2784
∴ SP of 1 article = ₹ \(\frac { 2784 }{ 80 } \) = ₹ 34.80
Hence, the selling price of one article is ₹ 34.80.

Question 4.
The cost of an article was ₹ 15,500, ₹450 were spent on its repairs. If it is sold for a profit of 15%, find the selling price of the article.
Solution.
CP of the article = ₹ 15,500
Money spent on its rapair = ₹ 450
Total CP of the article = ₹ 15,500 + ₹ 450
(overhead expenses)
= ₹ 15,950
Profit = 15% of ₹ 15,950
= ₹ \(\frac { 15 }{ 100 } \times 15,950\) = ₹ 2392.50
.-. SP of the article
= CP + Profit
=₹ 15,950 + ₹ 2392.50
= ₹ 18342.50
Hence, the selling price of the article is ₹ 18342.50.

Question 5.
A VCR and TV mere bought for ₹ 8,000 each. The shopkeeper made a loss of 4% on the VCR and a profit of 8% on TV. Find the gain or loss percent on the whole transaction.
Solution.
Combined CP of VCR and TV
= ₹ 8,000 + ₹ 8,000 = ₹ 16,000

Question 6.
During a sale, a shop offered a discount of 10% on the marked prices of all the items. What would a customer have to pay for a pair of jeans marked at ₹ 1450 and two shirts marked at ₹ 850 each?
Solution.
For a pair of jeans
Marked price = ₹ 1450
Discount rate = 10%
Discount = 10% of ₹ 1450
= ₹ \(\frac { 10 }{ 100 } \times 1450\) = ₹ 145
∴ Sale price = Marked price – Discount
= ₹ 1450- ₹ 145 = ₹ 1305
For two shirts
Marked price = ₹ 850 x 2 = ₹ 1700
Discount rate = 10%
∴ Discount
= 10% of ₹ 1700
₹ \(\frac { 10 }{ 100 } \times 1700\) x 1700 = ₹ 170
∴ Sale price
= Marked price – Discount
= ₹ 1700 – ₹ 170 =₹ 1530
Total payment made by customer
= ₹ 1305 + ₹ 1530 = ₹ 2835
Hence, the customer will have to pay ₹ 2835 for a pair of jeans and two shirts.

Question 7.
A milkman sold two of his buffaloes for ₹ 20,000 each. On one he made a gain of 5% and on the other a loss of 10%. Find his overall gain or loss. (Hint: Find CP of each.)
Solution.
Combined SP
= ₹ 20,000 x 2 = ₹ 40,000
For first buffalo

Question 8.
The price of a TV is ₹ 13,000. The sales tax charged on it is at the rate of 12%. Find the amount that Vinod will have to pay if he buys it.
Solution.
Price of TV = ₹ 13,000
Sales tax charged on it
= 12% of ₹ 13,000
= ₹ \(\frac { 12 }{ 100 } \times 13,000\) = ₹ 1560
∴ Amount to be paid
= Price + Sales Tax
= ₹ 13,000 + ₹ 1,560
= ₹ 14,560.
Hence, the amount that Vinod will have to pay for the TV if he buys it is ₹ 14,560.

Question 9.
Arun bought a pair of skates at a sale where the discount is given was 20%. If the amount he pays is ₹ 1,600, find the marked price.
Solution.
Amount paid = ₹ 1600
Discount rate = 20%.
100 – 20 = 80
∵ If amount paid is ₹ 80, then the marked price = ₹ 100
∴ If amount paid is ₹ 1, then the marked price = ₹ \(\frac { 100 }{ 80 } \)
∴ If amount paid is ₹ 1600, then the marked price = \(\frac { 100 }{ 80 } \times 1600\) = ₹ 2000
Hence, the marked price of the pair of skates is ₹ 2000.
Aliter:
Let the market price of the pair of shoes be ₹ 100.
Rate of discount = 20%
∴ Discount = 20% of ₹ 100
= \(\frac { 20 }{ 100 } \times 100\) = ₹ 20
∴ Sale price = Marked price – Discount
= ₹ 100 – ₹ 20 = ₹ 80
∵ If the sale price is ₹ 80, then, the marked price = ₹ 100
∴ If the sale price is ₹ 1, then the marked price = ₹ \(\frac { 100 }{ 80 } \)
∴ If the sale price is ₹ 1600, then the marked price = ₹ \(\frac { 100 }{ 80 } \times 1600\) = ₹ 2000
Hence, the marked price of the pair of shoes is ₹ 2000.

Question 10.
I purchased a hair-dryer for ₹ 5,400 including 8% VAT. Find the price before VAT was added.
Solution.
Price of hair-dryer including VAT = ₹ 5400
VAT rate = 8%
100 + 8 = 108
∵ When price including VAT is ₹ 108,
original price = ₹ 100
∴ When price including VAT is ₹ 5,400,
original price = ₹ \(\frac { 100 }{ 108 } \times \left( 5,400 \right) \) = ₹ 5,000
Hence, the price before VAT was added is ₹ 5,000.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.2 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 8 Comparing Quantities Ex 8.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.2.

• Cubes and Cube Roots Class 8 Ex 7.1

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 7
Chapter Name	Cubes and Cube Roots
Exercise	Ex 7.2
Number of Questions Solved	4
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.2

Question 1.
Find the cube root of each of the following numbers by prime factorisation method:
(i) 64
(ii) 512
(iii) 10648
(iv) 27000
(v) 15625
(vi) 13824
(vii) 110592
(viii) 46656
(ix) 175616
(x) 91125
Solution.
(i) 64

(ii) 512

(iii) 10648

(iv) 27000

(v) 15625

(vi) 13824

(vii) 110592

(viii) 46656

(ix) 175616

(x) 91125

Question 2.
State true or false:
(i) Cube of any odd number is even,
(ii) A perfect cube does not end with two zeros.
(iii) If square of a number ends with 5, then its cube ends with 25.
(iv) There is no perfect cube which ends with 8.
(v) The cube of a two digit number may be a three digit number.
(vi) The cube of a two digit number may have seven or more digits.
(vii) The cube of a single digit number may be a single digit number.
Solution.
(i) False
(ii) True
(iii) False ⇒ \({ 15 }^{ 2 }\) = 225, \({ 15 }^{ 3 }\) = 3375
(iv) False ⇒ \({ 12 }^{ 3 }\) = 1728
(v) False ⇒ \({ 10 }^{ 3 }\) = 1000, \({ 99 }^{ 3 }\) = 970299
(vi) False ⇒ \({ 10 }^{ 3 }\) = 1000, \({ 99 }^{ 3 }\) = 970299
(vii) True ⇒ \({ 1 }^{ 3 }\) = 1; \({ 2 }^{ 3 }\) = 8

Question 3.
You are told that 1,331 is a perfect cube. Can you guess without factorization what is its cube root? Similarly, guess the cube roots of 4913, 12167, 32768.
Solution.
By guess,
Cube root of 1331 =11
Similarly,
Cube root of 4913 = 17
Cube root of 12167 = 23
Cube root of 32768 = 32
EXPLANATIONS
(i)
Cube root of 1331
The given number is 1331.

Step 1. Form groups of three starting from the rightmost digit of 1331. 1 331
In this case, one group i.e., 331 has three digits whereas 1 has only 1 digit.
Step 2. Take 331.
The digit 1 is at one’s place. We take the one’s place of the required cube root as 1.
Step 3. Take the other group, i.e., 1. Cube of 1 is 1.
Take 1 as ten’s place of the cube root of 1331.
Thus, \(\sqrt [ 3 ]{ 1331 } =11\)

(ii)
Cube root of 4913
The given number is 4913.

Step 1. Form groups of three starting from the rightmost digit of 4913.
In this case one group, i.e., 913 has three digits whereas 4 has only one digit.
Step 2. Take 913.
The digit 3 is at its one’s place. We take the one’s place of the required cube root as 7.
Step 3. Take the other group, i.e., 4. Cube of 1 is 1 and cube of 2 is 8. 4 lies between 1 and 8.
The smaller number among 1 and 2 is 1.
The one’s place of 1 is 1 itself. Take 1 as ten’s place of the cube root of 4913.
Thus, \(\sqrt [ 3 ]{ 4913 } =17\)

(iii)
Cube root of 12167
The given number is 12167.

Step 1. Form groups of three starting from the rightmost digit of 12167.
12 167. In this case, one group, i. e., 167 has three digits whereas 12 has only two digits.
Step 2. Take 167.
The digit 7 is at its one’s place. We take the one’s place of the required cube root as 3.
Step 3. Take the other group, i.e., 12. Cube of 2 is 8 and cube of 3 is 27. 12 lies between 8 and 27. The smaller among 2 and 3 is 2.
The one’s place of 2 is 2 itself. Take 2 as ten’s place of the cube root of 12167.
Thus, A/12167 = 23.
Thus, \(\sqrt [ 3 ]{ 12167 } =23\).

(iv)
Cube root of 32768
The given number is 32768.

Step 1. Form groups of three starting from the rightmost digit of 32768.
32 768. In this case one group,
i. e., 768 has three digits whereas 32 has only two digits.
Step 2. Take 768.
The digit 8 is at its one’s place. We take the one’s place of the required cube root as 2.
Step 3. Take the other group, i.e., 32.
Cube of 3 is 27 and cube of 4 is 64.
32 lies between 27 and 64.
The smaller number between 3 and 4 is 3.
The ones place of 3 is 3 itself. Take 3 as ten’s place of the cube root of 32768.
Thus, \(\sqrt [ 3 ]{ 32768 } =32\).

 

We hope the NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.2 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 7 Cubes and Cube Roots Ex 7.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.4 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.4.

• Squares and Square Roots Class 8 Ex 6.1
• Squares and Square Roots Class 8 Ex 6.2
• Squares and Square Roots Class 8 Ex 6.3

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 6
Chapter Name	Squares and Square Roots
Exercise	Ex 6.4
Number of Questions Solved	9
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.4

Question 1.
Find the square root of each of the following numbers by Division method:

Solution.
(i) 2304

(ii) 4489

(iii) 3481

(iv) 529

(v) 3249

(vi) 1369
(vii) 5776

(viii) 7921

(ix) 576

(x) 1024

(xi) 3136

(xii) 900

Question 2.
Find the number of digits in the square root of each of the following numbers (without any calculation):
(i) 64
(ii) 144
(iii) 4489
(iv) 27225
(v) 390625.
Solution.
(i) 64
Number (n) of digits in 64 = 2 which is even.
∴ Number of digits in the square root of 64 \(\frac { n }{ 2 } =\frac { 2 }{ 2 } =1\)

(ii) 144
Number (n) of digits in 144 = 3 which is
∴ Number of digits in the square root of 144 \(\frac { n+1 }{ 2 } =\frac { 3+1 }{ 2 } =\frac { 4 }{ 2 } =2\)

(iii) 4489
Number (n) of digits in 4489 = 4 which is even.
∴ Number of digits in the square root of 4489 \(\frac { n }{ 2 } =\frac { 4 }{ 2 } =2\)

(iv) 27225
Number (n) of digits in 27225 = 5 which is odd.
∴ Number of digits in the square root of 27225 \(\frac { n+1 }{ 2 } =\frac { 5+1 }{ 2 } =\frac { 6 }{ 2 } =3\)

(v) 390625
Number (n) of digits in 390625 = 6 which is even.
∴ Number of digits in the square root of 390625 \(\frac { n }{ 2 } =\frac { 6 }{ 2 } =3\)

Question 3.
Find the square root of the following decimal numbers:
(i) 2.56
(ii) 7.29
(iii) 51.84
(iv) 42.25
(v) 31.36
Solution.
(i) 2.56

(ii) 7.29

(iii) 51.84

(iv) 42.25

(v) 31.36

Question 4.
Find the least number which must be subtracted from each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 402
(ii) 1989
(iii) 3250
(iv) 825
(v) 4000
Solution.
(i)402

(ii) 1989

(iii) 3250

(iv) 825

(v) 4000

Question 5.
Find the least number which must be added to each of the following numbers so as to get a perfect square. Also find the square root of the perfect square so obtained.
(i) 525
(ii) 1750
(iii) 252
(iv) 1825
(v) 6412
Solution.
(i) 525

(ii) 1750

(iii) 252

(iv) 1825

(v) 6412

Question 6.
Find the length of the side of a square whose area is 441 \({ m }^{ 2 }\).
Solution.
Area of the square = 441 \({ m }^{ 2 }\)
∴ Length of the side of the square

Question 7.
In a right triangle ABC, ∠B = 90°.
(a) If AB = 6 cm, BC = 8 cm, find AC
(b) If AC 13 cm, BC = 5 cm, find AB.
Solution.
(a) In the right triangle ABC,
∠B = 90°
Given

Question 8.
A gardener has 1000 plants. He wants to plant these in such a way that the number of rows and the number of columns remain same. Find the minimum number of plants he needs more for this.
Solution.
Let the number of rows be x.
Then the number of columns is x.

Question 9.
There are 500 children in a school. For a P.T. drill they have to stand in such a manner that the number of rows is equal to number of columns. How many children would be left out in this arrangement?
Solution.
Let the number of rows be x.
Then the number of columns is x.

We hope the NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.4 are part help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.4 are part, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.3 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.3.

• Squares and Square Roots Class 8 Ex 6.1
• Squares and Square Roots Class 8 Ex 6.2
• Squares and Square Roots Class 8 Ex 6.4

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 6
Chapter Name	Squares and Square Roots
Exercise	Ex 6.3
Number of Questions Solved	10
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.3

Question 1.
What could be the possible ‘one’s’ digits of the square root of each of the following numbers ?
(i) 9801
(ii) 99856
(iii) 998001
(iv) 657666025.
Solution.
(i) 9801
∵ 1 x 1 = 1 and 9 x 9 = 81
∵ The possible one’s digit of the square root of the number 9801 could be 1 or 9.

(ii) 99856
∵ 4 x 4 = 16 and 6 x 6 = 36
∵ The possible one’s digit of the square root of the number 99856 could be 4 or 6.

(iii) 998001
∵ 1×1 = 1 and 9 x 9 = 81
∵ The possible one’s digit of the square root of the number 998001 could be 1 or 9.

(iv) 657666025
∵ 5 x 5 = 25
∵ The possible one’s digit of the square root of the number 657666025 could be 5.

Question 2.
Without doing any calculation, find the numbers which are surely not perfect squares.
(i) 153
(ii) 257
(iii) 408
Solution.
(i) 153
The number 153 is surely not a perfect square because it ends in 3 whereas the square numbers end with 0, 1, 4, 5, 6 or 9.

(ii) 257
The number 257 is surely not a perfect square because it ends in 7 whereas the square numbers end with 0, 1, 4, 5, 6 or 9.

(iii) 408
The number 408 is surely not a perfect square because it ends in 8 whereas the square numbers end with 0, 1, 4, 5, 6 or 9.

(iv) 441
The number may be a perfect square as the square numbers end wTith 0, 1, 4, 5, 6 or 9.

Question 3.
Find the square roots of 100 and 169 by the method of repeated subtraction.
Solution.
(i) 100

• 100 – 1 = 99
• 99 – 3 = 96
• 96 – 5 = 91
• 91 – 7 = 84
• 84 – 9 = 75
• 75 – 11 = 64
• 64 – 13 = 51
• 51 – 15 = 36
• 36 – 17 = 19
• 19 – 19 = 0

Since from 100, we subtracted successive odd numbers starting from 1 and obtained 0 at the 10th step, therefore,
\(\sqrt { 100 } =10\)

(ii) 169

• 169 – 1 = 168
• 168 – 3 = 165
• 165 – 5 = 160
• 160 – 7 = 153
• 153 – 9 = 144
• 144-11 = 133
• 133 – 13 = 120
• 120 – 15 = 105
• 105 – 17 = 88
• 88 – 19 = 69
• 69 – 21 = 48
• 48 – 23 = 25
• 25 – 25 = 0

Since rom 169, we subtracted successive odd numbers starting from 1 and obtained 0 at the 13th step, therefore,
\(\sqrt { 169 } =13\)

Question 4.
Find the square roots of the following numbers by the Prime Factorisation Method:
(i) 729
(ii) 400
(iii) 1764
(iv) 4095
(v) 7744
(vi) 9604
(vii) 5929
(viii) 9216
(ix) 529
(x) 8100
Solution.
(i) 729
The prime factorisation of 729 is
729 = 3 x 3 x 3 x 3 x 3 x 3.

(ii) 400
The prime factorisation of 400 is
400 = 2 x 2 x 2 x 2 x 5 x 5.

(iii) 1764

(iv) 4096

(v) 7744

(vi) 9604

(vii) 5929

(viii) 9216

(ix) 529

(x) 8100

Question 5.
For each of the following numbers, find the smallest whole number by which it should be multiplied so as to get a perfect square number. Also find the square root of the square number so obtained.
(i) 252
(ii) 180
(iii) 1008
(iv) 2028
(v) 1458
(vi) 768
Solution.
(i) 252

(ii) 180

(iii) 1008

(iv) 2028

(v) 1458

(vi) 768

Question 6.
For each of the following numbers, find the smallest whole number by which it should be divided so as to get a perfect square. Also find the square root of the square number so obtained.
(i) 252
(ii) 2925
(iii) 396
(iv) 2645
(v) 2800
(vi) 1620
Solution.
(i) 252

(ii) 2925

(iii) 396

(iv) 2645

(v) 2800

(vi) 1620

Question 7.
The students of Class VIII of a school donated? 2401 in all, for Prime Minister’s National Relief Fund. Each student donated as rr’iny rupees as the number of students in the class. Find the number of students in the class.
Solution.
Let the number of students in the class be x.

Question 8.
2025 plants are to be planted in a garden in such a way that each row contains as many plants as the number of rows. Find the number of rows and the number of plants in each row.
Solution.
Let the number of rows be x.
Then, number of plants in each row = x.

Question 9.
Find the smallest square number that is divisible by each of the numbers 4, 9 and 10.
Solution.

In order to get a perfect square, each factor of 180 must be paired. So, we need to make pair of 5.
Therefore, 180 should be multiplied by 5.
Hence, the required smallest square number is 180 x 5 = 900.

Question 10.
Find the smallest square number that is divisible by each of the numbers 8, 15 and 20.
Solution.

 

We hope the NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.3 are part help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.3 are part, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.2 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.2.

• Squares and Square Roots Class 8 Ex 6.1
• Squares and Square Roots Class 8 Ex 6.3
• Squares and Square Roots Class 8 Ex 6.4

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 6
Chapter Name	Squares and Square Roots
Exercise	Ex 6.2
Number of Questions Solved	2
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.2

Question 1.
Find the square of the following numbers:
(i) 32
(ii) 35
(iii) 86
(iv) 93
(v) 71
(vi) 46
Solution.
(i) 32
32 = 30 + 2
Therefore, \({ 32 }^{ 2 }\) = \({ \left( 30+2 \right) }^{ 2 }\)
= 30 (30 + 2) + 2 (30 + 2)
= 900 + 60 + 60 + 4
= 1024

(ii) 35
35 = 30 + 5
Therefore, \({ 35 }^{ 2 }\) = \({ \left( 30+5 \right) }^{ 2 }\)
= 30 (30 + 5) + 5 (30 + 5)
= 900 + 150 + 150 + 25
= 1225

(iii) 86
86 = 80 + 6
Therefore, \({ 86 }^{ 2 }\)= \({ \left( 80+6 \right) }^{ 2 }\)
= 80 (80 + 6) + 6 (80 + 6)
= 6400 + 480 + 480 + 36
= 7396

(iv) 93
93 = 90 + 3
Therefore, \({ 90 }^{ 2 }\)= \({ \left( 90+3\right) }^{ 2 }\)
= 90 (90 + 3) + 3 (90 + 3)
= 8100 + 270 + 270 + 9
= 8649

(v) 71
71 = 70 + 1
Therefore, \({ 70 }^{ 2 }\)= \({ \left( 70+1\right) }^{ 2 }\)
= 70 (70 + 1) + 1 (70 + 1)
= 4900 + 70 + 70 + 1
= 5041

(vi) 46
46 = 40 + 6
Therefore, \({ 40 }^{ 2 }\)= \({ \left( 40+6\right) }^{ 2 }\)
= 40 (40 + 6) + 6 (40 + 6)
= 1600 + 240 + 240 + 36
= 2116

Question 2.
Write a Pythagorean triplet whose one number is
(i) 6
(ii) 14
(iii) 16
(iv) 18
Solution.
(i) 6
Let 2m = 6
⇒ \(m=\frac { 6 }{ 2 } =3\)

(ii) 14
Let 2m = 14

(iii) 16
Let 2m = 16

(iv) 18
Let 2m = 18

We hope the NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.2 are part help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 6 Squares and Square Roots Ex 6.2 are part, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.3 are part of NCERT Solutions for Class 8 Maths. Here we have given NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.3.

• Data Handling Class 8 Ex 5.1
• Data Handling Class 8 Ex 5.2

Board	CBSE
Textbook	NCERT
Class	Class 8
Subject	Maths
Chapter	Chapter 5
Chapter Name	Data Handling
Exercise	Ex 5.3
Number of Questions Solved	6
Category	NCERT Solutions

NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.3

Question 1.
List the outcomes you can see in these experiments.
(a) Spinning a wheel

(b) Tossing two coins together
Solution.
(a) Outcomes in spinning the given wheel are A, B, C and D.
(b) Outcomes in tossing two coins together are HT, HH, TH, TT (Here HT means Head on first coin and Tail on the second coin and so on).

Question 2.
When a die is thrown, list the outcomes of an event of getting
(i)
(a) a prime number
(b) not a prime number

(ii)
(a) a number greater than 5
(b) a number not greater than 5.
Solution.
Possible outcomes are:
1, 2, 3, 4, 5, and 6.
Out of these, prime numbers are
2, 3 and 5.

(i)
(a) Outcomes of an event of getting a prime number are: 2, 3 and 5
(b) Outcomes of an event of not getting a prime number are 1, 4 and 6.

(ii)
(a) Outcomes of an event of getting a number greater than 5 are 6
(b) Outcomes of an event of getting a; number not greater than 5 are 1, 2, 3, 4 and 5.

Question 3.
Find the
(a) Probability of the pointer stopping on D in (Question l-(a))?
(b) Probability of getting an ace from a j well shuffled deck of 52 playing cards?
(c) Probability of getting a red apple. (See figure)

Solution.
(a) There are in all 5 outcomes of the event. These are A, B, C and D. The pointer stopping on D has only 1 outcome, i.e., D
∴ Probability of the pointer stopping on D =\(\frac { 1 }{ 5 } \)

(b) Total number of playing cards = 52 Number of possible outcomes = 52
Number of aces in a deck of playing cards = 4
cards = 4
∴ Probability of getting an ace from a well shuffled deck of 52
playing cards = \(\frac { 4 }{ 52 } \) = \(\frac { 1 }{ 13 } \)

(c) Total number of apples = 7
Number of red apples = 4
∴ Probability of getting a red apple = \(\frac { 4 }{7} \)

Question 4.
Numbers 1 to 10 are written on ten separate slips (one number on one slip), kept in a box and mixed well. One slip is chosen from the box without looking into it. What is the probability of?
(i) getting a number 6?
(ii) getting a number less than 6?
(iii) getting a number greater than 6?
(iv) getting a 1-digit number?
Solution.
Total number of outcomes of the event (1, 2, 3, 4, 5, 6, 7, 8, 9 and 10) = 10
(i)
∵ Number of outcomes of getting a number 6=1
∴ Probability of getting a number \(\frac { 1 }{10} \)

(ii)
∵ There are 5 numbers (1, 2, 3, 4 and 5) less than 6.
∴ Number of outcomes of getting a number less than 6 = 5
∴ Probability of getting a number less than \(6=\frac { 5 }{ 10 } =\frac { 1 }{ 2 } \)

(iii)
∵ There are 4 numbers (7, 8, 9 and 10) greater than 6
∴ Number of outcomes of getting a number greater than 6 = 4
∴ Probability of getting a number greater than \(6=\frac { 4 }{ 10 } =\frac { 2}{ 15 } \)

(iv)
∵ There are 9 1-digit numbers (1, 2, 3, 4, 5, 6, 7, 8 and 9)
∴ Number of outcomes of getting a 1-digit number = 9
∴ Probability of getting a 1-digit number \(=\frac { 9 }{ 10 } \)

Question 5.
If you have a spinning wheel with 3 green sectors, 1 blue sector and 1 red sector, what is the probability of getting a green sector? What is the probability of getting a nonblue sector?
Solution.
Number of green sectors = 3
Number of blue sectors = 1
Number of red sectors = 1
∴ Total number of sectors = 3 + 1 + 1=5
∴ Total number of outcomes of the event = 5
Number of outcomes of getting a green sector = 3
∴ Probability of getting a green sector = \(\frac { 3 }{ 5 } \)
Number of outcomes of getting a non-blue sector = Number of green sectors + Number of red sectors
=3+1=4
∴ Probability of getting a non-blue sector = \(\frac { 4 }{ 5 } \).

Question 6.
Find the probabilities of the events given in Question 2.
Solution.
Total number of outcomes of the event (1, 2, 3, 4, 5 and 6) = 6
(i)
(a) Number of prime numbers (2, 3 and 5) = 3
∴ Number of outcomes of getting a prime number = 3
∴ Probability of getting a prime number = \(\frac { 3 }{ 6 } =\frac { 1 }{ 2 } \).
(b) Number of non-prime numbers (1, 4 and 6) = 3
∴ Number of outcomes of getting a non-prime number = 3
∴ Probability of getting a non-prime number = \(\frac { 3 }{ 6 } =\frac { 1 }{ 2 } \).

(ii)
(a) Number greater than 5 = 6, i.e., only one.
∴ Number of outcomes of getting a number greater than 5 = 1
∴ Probability of getting a number greater than 5 = \(\frac { 1 }{ 6 } \).
(b) Number of numbers not greater than 5 (1, 2, 3, 4 and 5) = 5
∴ Number of outcomes of getting a number not greater than 5 = 5
∴ Probability of getting a number not greater than 5 = \(\frac { 5 }{ 6 } \).

We hope the NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.3 help you. If you have any query regarding NCERT Solutions for Class 8 Maths Chapter 5 Data Handling Ex 5.3, drop a comment below and we will get back to you at the earliest.