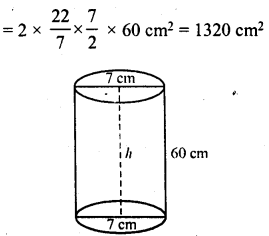
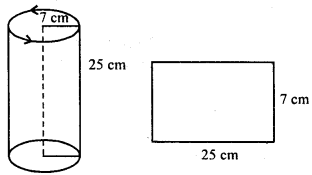
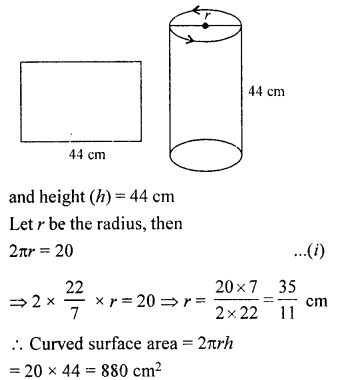
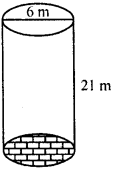
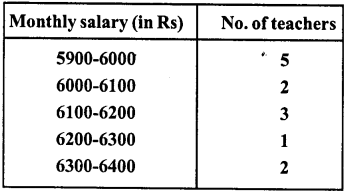
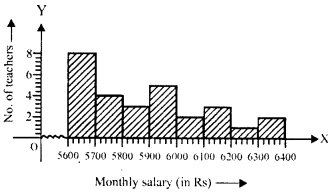
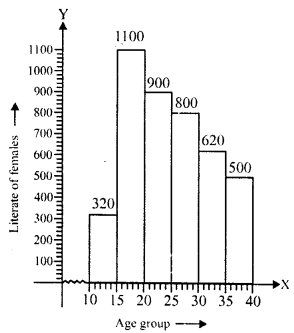
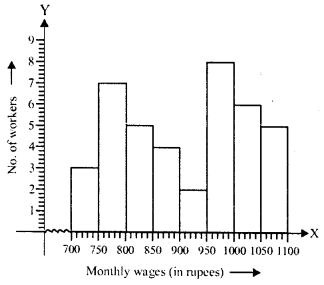
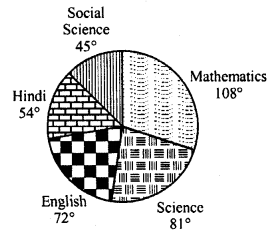
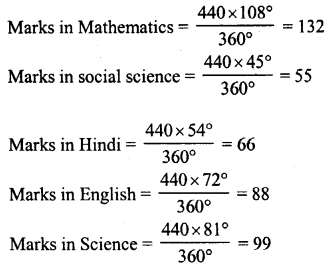
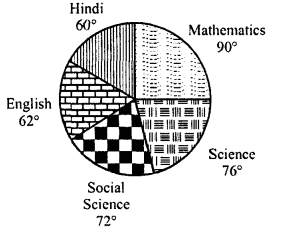
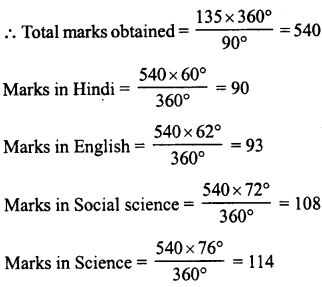
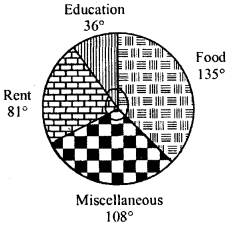
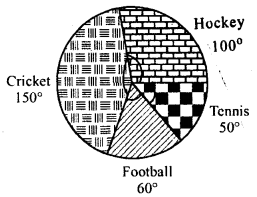
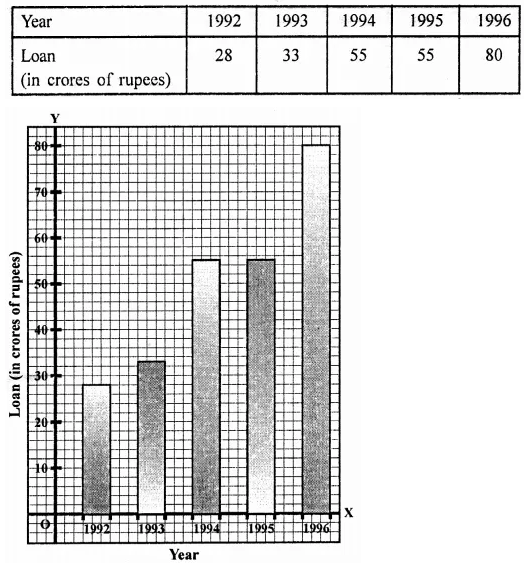
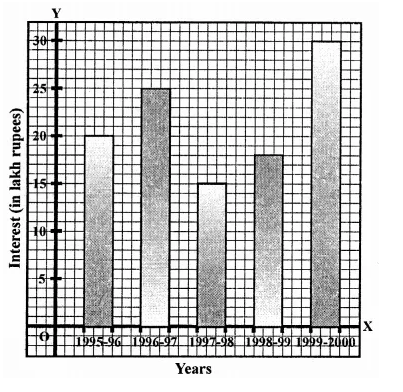
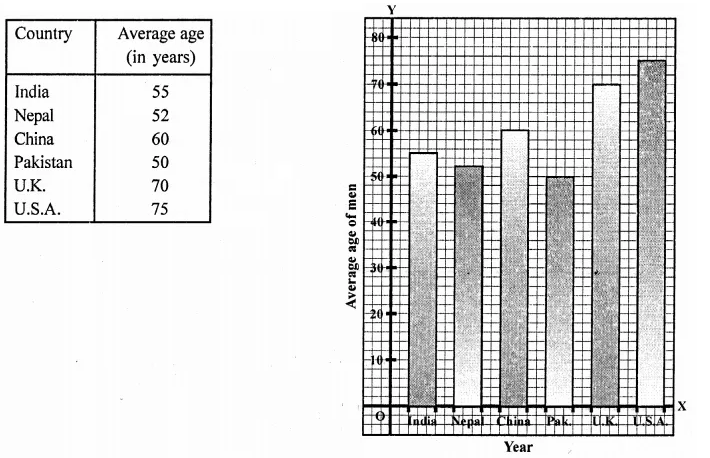
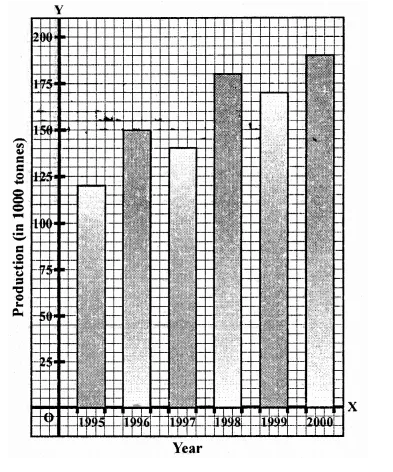
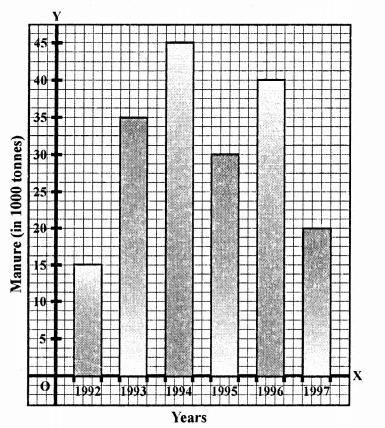
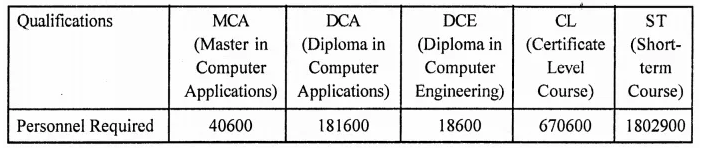
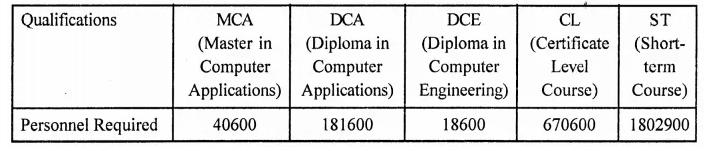
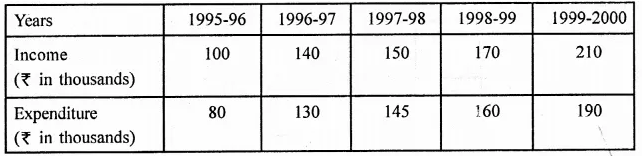
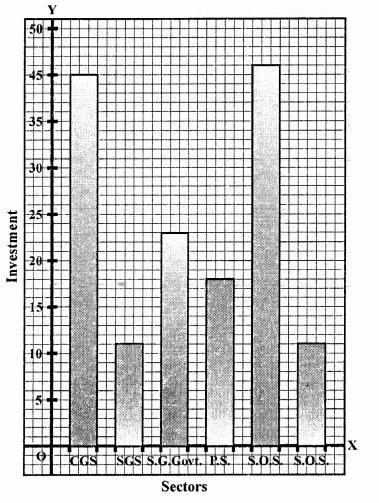
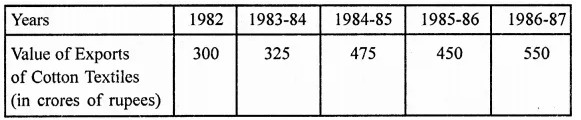
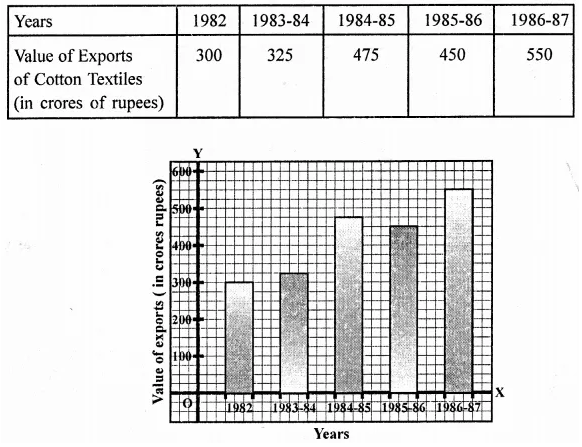
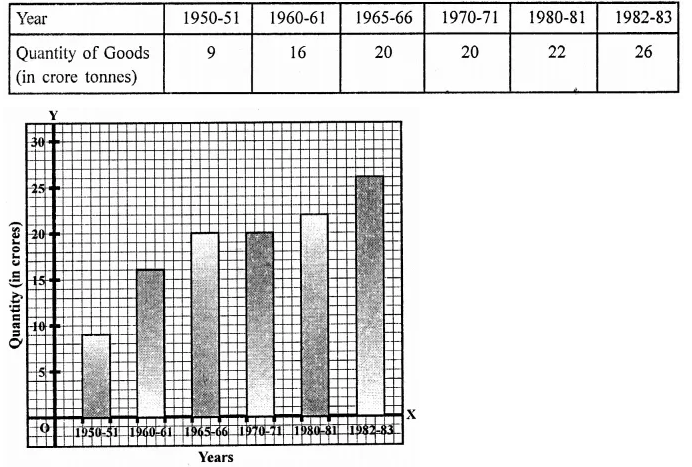
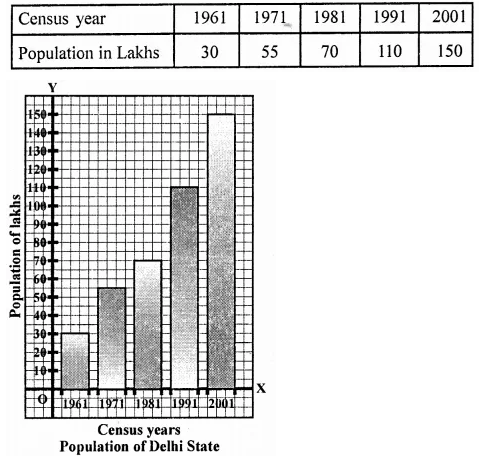
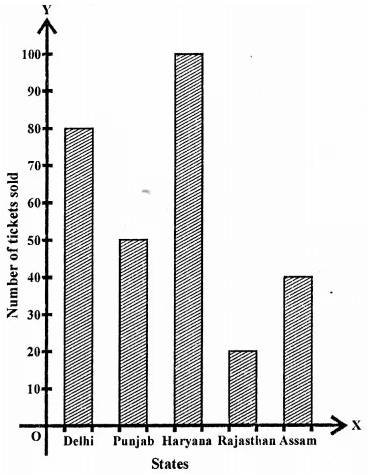
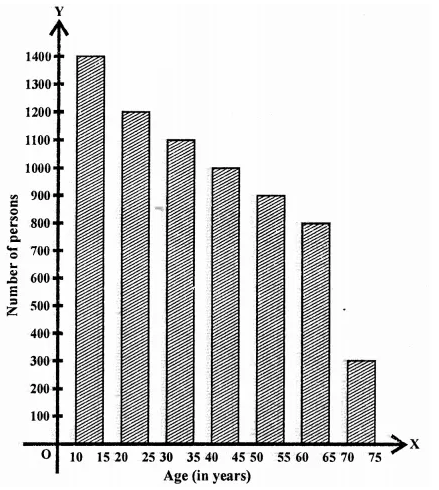
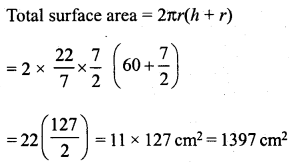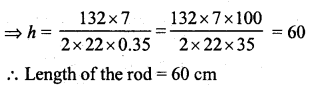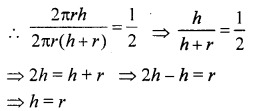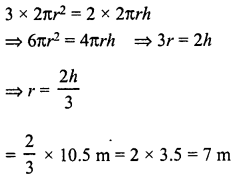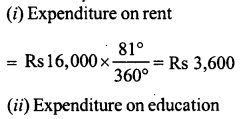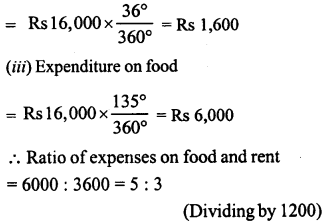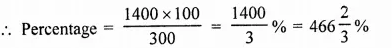NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.1 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.1.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 11 |
| Chapter Name | Circles |
| Exercise | Ex 11.1 |
| Number of Questions Solved | 2 |
| Category | NCERT Solutions |
NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.1
Question 1.
Fill in the blanks.
(i) The centre of a circle lies in ___ of the circle. (exterior/interior)
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in ____ of the circle, (exterior/interior)
(iii) The longest chord of a circle is a ____ of the circle.
(iv) An arc is a ____ when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and ____ of the circle.
(vi) A circle divides the plane, on which it lies, in ____ parts.
Solution:
(i) The centre of a circle lies in interior of the circle.
(ii) A point, whose distance from the centre of a circle is greater than its radius lies in exterior of the circle.
(iii) The longest chord of a circle is a diameter of the circle.
(iv) An arc is a semi-circle when its ends are the ends of a diameter.
(v) Segment of a circle is the region between an arc and chord of the circle.
(vi) A circle divides the plane, on which it lies, in three parts.
Question 2.
Write True or False. Give reason for your answers.
(i) Line segment joining the centre to any point on the circle is a , radius of the circle.
(ii) A circle has only finite number of equal chords.
(iii) If a circle is divided into three equal arcs, each is a major arc.
(iv) A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
(v) Sector is the region between the chord and its corresponding arc.
(vi) A circle is a plane figure.
Solution:
(i) True. Because all points are equidistant from the centre to the circle.
(ii) False. Because circle has infinitely may equal chords can be drawn.
(iii) False. Because all three arcs are equal, so their is no difference between the major and minor arcs.
(iv) True. By the definition of diameter, that diameter is twice the radius.
(v) False. Because the sector is the region between two radii and an arc.
(vi) True. Because circle is a part of the plane figure.
We hope the NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.1, help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 11 Circles Ex 11.1, drop a comment below and we will get back to you at the earliest.