Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.
Ionisation of Weak Acids
We have already learnt that weak acids are partially dissociated in water and there is an equilibrium between the undissociated acid and its dissociated ions. Consider the ionisation of a weak monobasic acid HA in water.
Applying law of chemical equilibrium, the equilibrium constant Kc is given by the expression
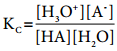 …………. (8.9)
…………. (8.9)
The square brackets, as usual, represent the concentrations of the respective species in moles per litre. In dilute solutions, water is present in large excess and hence, its concentration may be taken as constant say K. Further H3O+ indicates that hydrogen ion is hydrated, for simplicity it may be replaced by H+. The above equation may then be written as,
![]() ………….. (8.10)
………….. (8.10)
The product of the two constants KC and K gives another constant. Let it be Ka
![]() …………. (8.11)
…………. (8.11)
The constant Ka is called dissociation constant of the acid. Like other equilibrium constants, Ka also varies only with temperature. Similarly, for a weak base, the dissociation constant can be written as below.
![]() ………….. (8.12)
………….. (8.12)
Ostwald’s Dilution Law
Ostwald’s dilution law relates the dissociation constant of the weak acid (Ka) with its degree of dissociation (α) and the concentration (c). Degree of dissociation (α) is the fraction of the total number of moles of a substance that dissociates at equilibrium.
![]()
We shall derive an expression for ostwald’s law by considering a weak acid, i.e. acetic acid (CH3COOH). The dissociation of acetic acid can be represented as
CH3COOH ⇄ H+ + CH3COO–
The dissociation constant of acetic acid is,
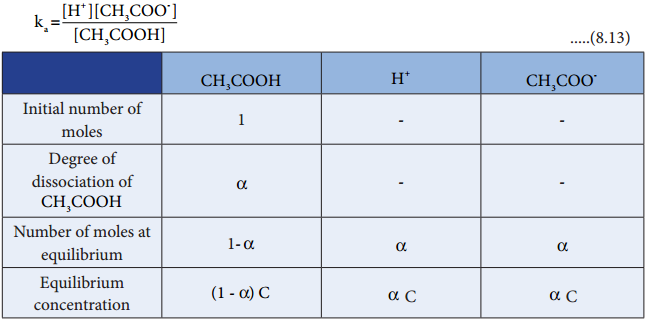
Substituting the equilibrium concentration in equation (8.13)
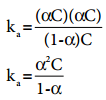 …………. (8.14)
…………. (8.14)
We know that weak acid dissociates only to a very small extent. Compared to one, α is so small and hence in the denominator (1 – α) ~ 1. The above expression (8.14) now becomes,
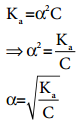 ………….. (8.15)
………….. (8.15)
Let us consider an acid with Ka value 4 × 10-4 and calculate the degree of dissociation of that acid at two different concentration 1 × 10-2M and 1 × 10-4M using the above expression (8.15) For 1 × 10-2M,
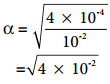
= 2 × 10-1
= 0.2
For 1 × 10-4M
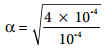
= 2
When the dilution increases by 100 times, (Concentration decreases from 1 × 10-2M to 1 × 10-2M), the dissociation increases by 10 times. Thus, we can conclude that, when dilution increases, the degree of dissociation of weak electrolyte also increases. This statement is known as Ostwald’s dilution Law.
The concentration of H+ (H3O+) can be caluculated using the Ka value as below.
[H+] = αC (Refer table) ………….. (8.16)
Equilibrium molar concentration of [H+] is equal to αC

Similarly, for a weak base
Kb = α2 and α = \(\sqrt{\frac{K_{b}}{C}}\)
[OH–] = αC
(or)
[OH–] = \(\sqrt{\mathrm{K}_{\mathrm{b}} \mathrm{C}}\) ………….. (8.18)
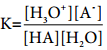 ………… (8.1)
………… (8.1)