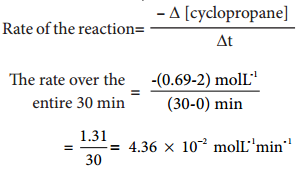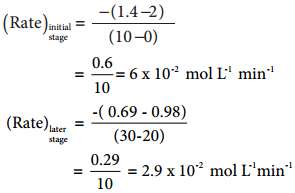Category: Chemistry

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Rate Law and Rate Constant

Rate Law and Rate Constant:

We have just learnt that, the rate of the reaction depends upon the concentration of the reactant. Now let us understand how the reaction rate is related to concentration by considering the following general reaction.

xA + yB → products

The rate law for the above reaction is generally expressed as Rate = k [A]^m[B]ⁿ

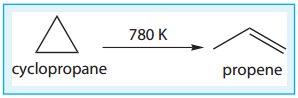
Where k is proportionality constant called the rate constant. The values of m and n represent the reaction order with respect to A and B respectively. The overall order of the reaction is given by (m+n). The values of the exponents (m and n) in the rate law must be determined by experiment. They cannot be deduced from the Stoichiometry of the reaction. For example, consider the isomerisation of cyclopropane, that we discussed earlier.

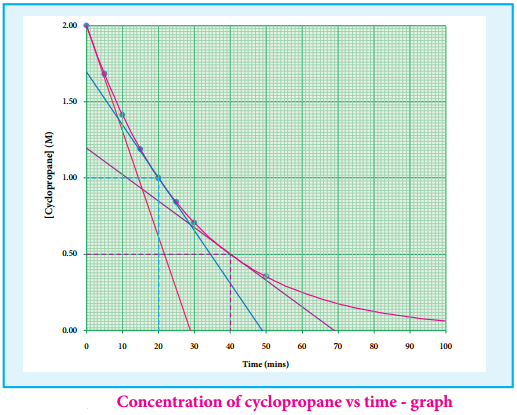
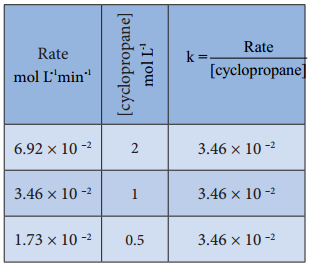
The results shown in table 7.2 indicate that if the concentration of cyclopropane is reduced to half, the rate also reduced to half. It means that the rate depends upon [cyclopropane] raised to the first power i.e., Rate = k[cyclopropane]¹

⇒ \(\frac{Rate}{[cyclopropane]}\) = k

Rate Constant for Isomerisation

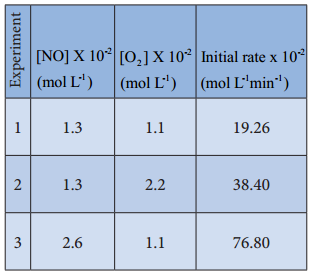
Let us consider an another example, the oxidation of nitric oxide (NO)

2NO(g) + O₂(g) → 2NO₂(g)

Series of experiments are conducted by keeping the concentration of one of the reactants constant and the changing the concentration of the others.

Rate = k [NO]^m[O₂]ⁿ
For experiment 1, the rate law is
Rate₁ = k [NO]^m[O₂]ⁿ
19.26 × 10^-2 = k[1.3]^m[1.1]ⁿ ………….. (1)
Similarly for experiment 2
Rate₂ = k[NO]^m[O₂]ⁿ
38.40 × 10^-2 = k[1.3]^m[2.2]ⁿ …………… (2)
For experiment 3
Rate₃ = k[NO]^m[O₂]ⁿ
76.8 × 10^-2 = k[2.6]^m[1.1]ⁿ …………….. (3)

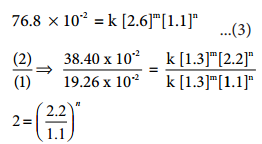
2=2ⁿ i.e., n = 1

Therefore the reaction is first order with respect to O₂

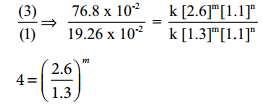
4=2^m i.e., m = 2

Therefore the reaction is second order with respect to NO

The rate law is Rate₁ = k[NO]²[O₂]¹
The overall order of the reaction = (2 + 1) = 3

Differences Between Rate and Rate Constant of a Reaction:

Rate of a Reaction	Rate Constant of a Reaction
1. It represents the speed at which the reactants are converted into products at any instant.	1. It is a proportionality constant.
2. It is measured as decrease in the concentration of the reactants or increase in the concentration of products.	2. It is equal to therate of reaction, when the concentration of each of the reactants is unity
3. It depends on the initial concentration of reactants.	3. It does not depend on the initial concentration of reactants.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Rate of a Chemical Reaction

A rate is a change in a particular variable per unit time. You have already learnt in physics that change in the displacement of a particle per unit time gives its velocity. Similarly in a chemical reaction, the change in the concentration of the species involved in a chemical reaction per unit time gives the rate of a reaction.

Let us consider a simple general reaction

A → B

The concentration of the reactant ([A]) can be measured at different time intervals. Let the concentration of A at two different times t₂ and t₂, (t₂ > t₁) be [A₁] and [A₂] respectively. The rate of the reaction can be expressed as

During the reaction, the concentration of the reactant decreases i.e. [A₂] < [A₁] and hence the change in concentration [A₂] [A₁] gives a negative value. By convention the reaction rate is a positive one and hence a negative sign is introduced in the rate expression (equation 7.1).

If the reaction is followed by measuring the product concentration, the rate is given by (\(\frac{∆[B]}{∆t}\)) since [B₂] > [B₁], no minus sign is required here.

Change in Concentration of A and B for the Reaction A → B

Unit of Rate of a Reaction:

Usually, concentration is expressed in number of moles per litre and time is expressed in seconds and therefore the unit of the rate of a reaction is mol L^-1s^-1. Depending upon the nature of the reaction, minute, hour, year etc can also be used. For a gas phase reaction, the concentration of the gaseous species is usually expressed in terms of their partial pressures and in such cases the unit of reaction rate is atm s^-1.

Stoichiometry and Rate of a Reaction:

In a reaction A → B, the stoichiometry of both reactant and product are same, and hence the rate of disappearance of reactant (A) and the rate of appearance of product (B) are same. Now, let us consider a different reaction

A → 2B

In this case, for every mole of A, that disappears two moles of B appear, i.e., the rate of formation of B is twice as fast as the rate of disappearance of A. therefore, the rate of the reaction can be expressed as below.

Rate = \(\frac{+d[B]}{dt}\) = 2(-\(\frac{d[A]}{dt}\)) In other words,
Rate = \(\frac{-d[A]}{dt}\) = \(\frac{1}{2}\) \(\frac{d[B]}{dt}\)

For a general reaction, the rate of the reaction is equal to the rate of consumption of a reactant (or formation of a product) divided by its coeffcient in the balanced equation

xA + yB → lC + mD
Rate = \(\frac{-1}{x}\) \(\frac{d[A]}{dt}\) = \(\frac{-1}{y}\) \(\frac{d[B]}{dt}\)
= \(\frac{1}{l}\) \(\frac{d[C]}{dt}\)
= \(\frac{1}{m}\) \(\frac{d{D]}{dt}\)

Average and Instantaneous Rate:

Let us understand the average rate and instantaneous rate by considering the isomerisation of cyclopropane.

The kinetics of the above reaction is followed by measuring the concentration of cyclopropane at regular intervals and the observations are shown below. (Table 7.1)

Concentration of Cyclopropane at various times during its Isomerisation at 780K

table 1

It means that during the first 30 minutes of the reaction, the concentration of the reactant (cyclo propane) decreases as an average of 4.36 × 10^-2 mol L^-1 each minute.

Let us calculate the average rate for an initial and later stage over a short period.

From the above calculations, we come to know that the rate decreases with time as the reaction proceeds and the average rate cannot be used to predict the rate of the reaction at any instant. The rate of the reaction, at a particular instant during the reaction is called the instantaneous rate,

As ∆t → 0;
\(\frac{-∆[cyclopropane]}{∆t}\) = \(\frac{-∆[cyclopropane]}{dt}\)

A plot of [cyclopropane] Vs (time) gives a curve as shown in the figure 7.2. Instantaneous rate at a particular instant ‘t’ \(\frac{-d[cyclopropane]}{dt}\) is obtained by calculating the slope of a tangent drawn to the curve at that instant.

In general, the instantaneous reaction rate at a moment of mixing the reactants (t = 0) is calculated from the slope of the tangent drawn to the curve. The rate calculated by this method is called initial rate of a reaction.

Let us calculate the instantaneous rate of isomerisation cyclopropane at different concentrations: 2M, 1M and 0.5M from the graph shown in fig 7.2, the results obtained are tabulated below.

Rate of Isomerisation

table 2

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Imperfection in Solids

According to the law of nature nothing is perfect, and so crystals need not be perfect. They always found to have some defects in the arrangement of their constituent particles. These defects affect the physical and chemical properties of the solid and also play an important role in various processes. For example, a process called doping leads to a crystal imperfection and it increases the electrical conductivity of a semiconductor material such as silicon.

The ability of ferromagnetic material such as iron, nickel etc., to be magnetized and demagnetized depends on the presence of imperfections. Crystal defects are classified as follows

1. Point defects
2. Line defects
3. Interstitial defects
4. Volume defects

In this portion, we concentrate on point defects, more specifically in ionic solids. Point defects are further classified as follows.

Stoichiometric Defects in Ionic Solid:

This defect is also called intrinsic (or) thermodynamic defect. In stoichiometric ionic crystals, a vacancy of one ion must always be associated with either by the absence of another oppositely charged ion (or) the presence of same charged ion in the interstitial position so as to maintain the electrical neutrality.

Schottky Defect:

Schottky defect arises due to the missing of equal number of cations and anions from the crystal lattice. This effect does not change the stoichiometry of the crystal. Ionic solids in which the cation and anion are of almost of similar size show schottky defect. Example: NaCl.

Presence of large number of schottky defects in a crystal, lowers its density. For example, the theoretical density of vanadium monoxide (VO) calculated using the edge length of the unit cell is 6.5 g cm^-3, but the actual experimental density is 5.6 g cm^-3. It indicates that there is approximately 14% Schottky defect in VO crystal. Presence of Schottky defect in the crystal provides a simple way by which atoms or ions can move within the crystal lattice.

Frenkel Defect:

Frenkel defect arises due to the dislocation of ions from its crystal lattice. The ion which is missing from the lattice point occupies an interstitial position. This defect is shown by ionic solids in which cation and anion differ in size. Unlike Schottky defect, this defect does not affect the density of the crystal. For example AgBr, in this case, small Ag⁺ ion leaves its normal site and occupies an interstitial position as shown in the figure.

Metal Excess Defect:

Metal excess defect arises due to the presence of more number of metal ions as compared to anions. Alkali metal halides NaCl, KCl show this type of defect. The electrical neutrality of the crystal can be maintained by the presence of anionic vacancies equal to the excess metal ions (or) by the presence of extra cation and electron present in interstitial position.

For example, when NaCl crystals are heated in the presence of sodium vapour, Na⁺ ions are formed and are deposited on the surface of the crystal. Chloride ions (Cl^–) diffuse to the surface from the lattice point and combines with Na⁺ ion.

The electron lost by the sodium vapour diffuse into the crystal lattice and occupies the vacancy created by the Cl^– ions. Such anionic vacancies which are occupied by unpaired electrons are called F centers. Hence, the formula of NaCl which contains excess Na⁺ ions can be written as Na_1+xCl.

ZnO is colourless at room temperature. When it is heated, it becomes yellow in colour. On heating, it loses oxygen and thereby forming free Zn²⁺ ions. The excess Zn²⁺ ions move to interstitial sites and the electrons also occupy the interstitial positions.

Metal Deficiency Defect:

Metal deficiency defect arises due to the presence of less number of cations than the anions. This defect is observed in a crystal in which, the cations have variable oxidation states. For example, in FeO crystal, some of the Fe²⁺ ions are missing from the crystal lattice.

To maintain the electrical neutrality, twice the number of other Fe²⁺ ions in the crystal is oxidized to Fe³⁺ ions. In such cases, overall number of Fe²⁺ and Fe³⁺ ions is less than the O^2- ions. It was experimentally found that the general formula of ferrous oxide is Fe_xO, where x ranges from 0.93 to 0.98.

Impurity Defect:

A general method of introducing defects in ionic solids is by adding impurity ions. If the impurity ions are in different valance state from that of host, vacancies are created in the crystal lattice of the host. For example, addition of CdCl₂ to AgCl yields solid solutions where the divalent cation Cd²⁺ occupies the position of Ag⁺. This will disturb the electrical neutrality of the crystal. In order to maintain the same, proportional number of Ag⁺ ions leaves the lattice. This produces a cation vacancy in the lattice, such kind of crystal defects are called impurity defects.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Packing in Crystals

Let us consider the packing of fruits for display in fruit stalls. They are in a closest packed arrangement as shown in the following fig we can extend this analogy to visualize the packing of constituents (atoms/ions/ molecules) in crystals, by treating them as hard spheres.

To maximize the attractive forces between the constituents, they generally tend to pack together as close as possible to each other. In this portion we discuss how to pack identical spheres to create cubic and hexagonal unit cell. Before moving on to these three dimensional arrangements, let us first consider the two dimensional arrangement of spheres for better understanding.

Linear Arrangement of Spheres in One Direction:

In a specific direction, there is only one possibility to arrange the spheres in one direction as shown in the fig. in this arrangement each sphere is in contact with two neighbouring spheres on either side.

Two Dimensional Close Packing:

Two dimensional planar packing can be done in the following two different ways.

(i) AAA Type:

Linear arrangement of spheres in one direction is repeated in two dimension i.e., more number of rows can be generated identical to the one dimensional arrangement such that all spheres of different rows align vertically as well as horizontally as shown in the fig.

If we denote the first row as A type arrangement, then the above mentioned packing is called AAA type, because all rows are identical as the first one. In this arrangement each sphere is in contact with four of its neighbours.

(ii) ABAB Type:

In this type, the second row spheres are arranged in such a way that they fit in the depression of the first row as shown in the figure. The second row is denoted as B type. The third row is arranged similar to the first row A, and the fourth one is arranged similar to second one. i.e., the pattern is repeated as ABAB.

In this arrangement each sphere is in contact with 6 of its neighbouring spheres. On comparing these two arrangements (AAAA…type and ABAB….type) we found that the closest arrangement is ABAB…type.

Simple Cubic Arrangement:

This type of three dimensional packing arrangements can be obtained by repeating the AAAA type two dimensional arrangements in three dimensions. i.e., spheres in one layer sitting directly on the top of those in the previous layer so that all layers are identical.

All spheres of different layers of crystal are perfectly aligned horizontally and also vertically, so that any unit cell of such arrangement as simple cubic structure as shown in fig. In simple cubic packing, each sphere is in contact with 6 neighbouring spheres Four in its own layer, one above and one below and hence the coordination number of the sphere in simple cubic arrangement is 6.

Packing Efficiency:

There is some free space between the spheres of a single layer and the spheres of successive layers. The percentage of total volume occupied by these constituent spheres gives the packing efficiency of an arrangement. Let us calculate the packing efficiency in simple cubic arrangement,

Let us consider a cube with an edge length ‘a’ as shown in fig. Volume of the cube with edge length a is = a × a × a = a³ Let ‘r’ is the radius of the sphere. From the figure, a = 2r ⇒r = \(\frac{a}{2}\)

∴ Volume of the sphere with radius ‘r’
= \(\frac{4}{3}\)πr³
= \(\frac{4}{3}\)π(\(\frac{a}{2}\))³
= \(\frac{4}{3}\)π(\(\frac{\mathrm{a}^{3}}{8}\))
= \(\frac{\pi \mathrm{a}^{3}}{6}\) ……………. (1)

In a simple cubic arrangement, number of spheres belongs to a unit cell is equal to one
∴ Total volume occupied by the spheres in sc unit cell = 1 × (\(\frac{\mathrm{a}^{3}}{6}\)) ……………… (2)
Dividing (2) by (3)
Packing Fraction = \(\frac{\left(\frac{\pi a^{3}}{6}\right)}{\left(a^{3}\right)}\) × 100 = \(\frac{100π}{6}\)
= 52.38%

i.e., only 52.38% of the available volume is occupied by the spheres in simple cubic packing, making inefficient use of available space and hence minimizing the attractive forces.

Body Centered Cubic Arrangement

In this arrangement, the spheres in the first layer (A type) are slightly separated and the second layer is formed by arranging the spheres in the depressions between the spheres in layer A as shown in figure. The third layer is a repeat of the first. This pattern ABABAB is repeated throughout the crystal. In this arrangement, each sphere has a coordination number of 8, four neighbors in the layer above and four in the layer below.

Packing Efficiency:

Here, the spheres are touching along the leading diagonal of the cube as shown in the fig.

In ∆ABC
AC² = AB² + BC²
AC = \(\sqrt{\mathrm{AB}^{2}+\mathrm{BC}^{2}}\)
AC = \(\sqrt{\mathrm{a}^{2}+\mathrm{a}^{2}}\) = \(\sqrt{2 a^{2}}\) = \(\sqrt{2}\)a

In ∆ACG

∴ Volume of the sphere with radius ‘r’

Number of spheres belong to a unit cell in bcc arrangement is equal to two and hence the total volume of all spheres

i.e., 68 % of the available volume is occupied. The available space is used more efficiently than in simple cubic packing.

The Hexagonal and Face Centered Cubic Arrangement:

Formation of First Layer:

In this arrangement, the first layer is formed by arranging the spheres as in the case of two dimensional ABAB arrangements i.e. the spheres of second row fit into the depression of first row. Now designate this first layer as ‘a’. The next layer is formed by placing the spheres in the depressions of the first layer. Let the second layer be ‘b’.

Formation of Second Layer:

In the first layer (a) there are two types of voids (or holes) and they are designated as x and y. The second layer (b) can be formed by placing the spheres either on the depression (voids/holes) x (or) on y let us consider the formation of second layer by placing the spheres on the depression (x).

Wherever a sphere of second layer (b) is above the void (x) of the first layer (a), a tetrahedral void is formed. This constitutes four spheres – three in the lower (a) and one in the upper layer (b). When the centers of these four spheres are joined, a tetrahedron is formed.

At the same time, the voids (y) in the first layer (a) are partially covered by the spheres of layer (b), now such a void in (a) is called a octahedral void. This constitutes six spheres – three in the lower layer (a) and three in the upper layer (b).

When the centers of these six spheres are joined, an octahedron is formed. Simultaneously new tetrahedral voids (or holes) are also created by three spheres in second layer (b) and one sphere of first layer (a).

Formation of Third Layer:

The third layer of spheres can be formed in two ways to acheive closest packing

• Aba arrangement – hcp structure
• Abc arrangement – ccp structure

The spheres can be arranged so as to fit into the depression in such a way that the third layer is directly over a first layer as shown in the figure. This “aba’’ arrangement is known as the hexagonal close packed (hcp) arrangement. In this arrangement, the tetrahedral voids of the second layer are covered by the spheres of the third layer.

Alternatively, the third layer may be placed over the second layer in such a way that all the spheres of the third layer fit in octahedral voids. This arrangement of the third layer is different from other two layers (a) and (b), and hence, the third layer is designated (c). If the stacking of layers is continued in abcabcabc pattern, then the arrangement is called cubic close packed (ccp) structure.

In both hcp and ccp arrangements, the coordination number of each sphere is 12 – six neighbouring spheres in its own layer, three spheres in the layer above and three sphere in the layer below. This is the most efficient packing.

The cubic close packing is based on the face centered cubic unit cell. Let us calculate the packing efficiency in fcc unit cell.

Total number of spheres belongs to a single fcc unit cell is 4

Radius Ratio:

The structure of an ionic compound depends upon the stoichiometry and the size of the ions.generally in ionic crystals the bigger anions are present in the close packed arrangements and the cations occupy the voids.

The ratio of radius of cation and anion (\(\frac{\mathrm{r}_{\mathrm{C}^{+}} {\mathrm{r}_{\mathrm{A}^{-}}}\)) plays an important role in determining the structure. The following table shows the relation between the radius ratio and the structural arrangement in ionic solids.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Primitive and Non-Primitive Unit Cell

There are two types of unit cells:

There are two types of unit cells primitive and non-primitive. A unit cell that contains only one type of lattice point is called a primitive unit cell, which is made up from the lattice points at each of the corners. In case of non-primitive unit cells, there are additional lattice points, either on a face of the unit cell or with in the unit cell.

There are seven primitive crystal systems; cubic, tetragonal, orthorhombic, hexagonal, monoclinic, triclinic and rhombohedral. They differ in the arrangement of their crystallographic axes and angles. Corresponding to the above seven, Bravis defined 14 possible crystal systems as shown in the figure.

Number of atoms in a cubic cell:

Primitive (or) Simple Cubic Unit Cell(SC)

In the simple cubic unit cell, each corner is occupied by an identical atoms or ions or molecules. And they touch along the edges of the cube, do not touch diagonally. The coordination number of each atom is 6. Each atom in the corner of the cubic unit cell is shared by 8 neighboring unit cells and therefore atoms per unit cell is equal to \(\frac{\mathrm{N}_{\mathrm{c}}}{8}\), where N_c is the number of atoms at the corners.
∴ Number of atoms in a SC unit cell = (\(\frac{Nc}{8}\))
= (\(\frac{8}{8}\)) = 1

Body Centered Cubic Unit Cell(BCC)

In a body centered cubic unit cell, each corner is occupied by an identical particle and in addition to that one atom occupies the body centre. Those atoms which occupy the corners do not touch each other, however they all touch the one that occupies the body centre.

Hence, each atom is surrounded by eight nearest neighbours and coordination number is 8. An atom present at the body centre belongs to only to a particular unit cell i.e unshared by other unit cell.
∴ Number of atoms in a bcc unit cell = (\(\frac{Nc}{8}\)) + (\(\frac{\mathrm{N}_{\mathrm{b}}}{1}\))
= (\(\frac{8}{8}\) + \(\frac{1}{1}\))
= (1 + 1)
= 2

Face Centered Cubic Unit Cell(FCC)

In a face centered cubic unit cell, identical atoms lie at each corner as well as in the centre of each face. Those atoms in the corners touch those in the faces but not each other. The atoms in the face centre is being shared by two unit cells, each atom in the face centers makes (\(\frac{1}{2}\)) contribution to the unit cell.
∴ Number of atoms in a fcc unitcell = (\(\frac{\mathrm{N}_{\mathrm{c}}}{8}\)) + (\(\frac{\mathrm{N}_{\mathrm{f}}}{8}\))
= (\(\frac{8}{8}\) + \(\frac{6}{2}\))
= (1 + 3)
= 4

Drawing the crystal lattice on paper is not an easy task. The constituents in a unit cell touch each other and form a three dimensional network. This can be simplified by drawing crystal structure with the help of small circles (spheres) corresponding constituent particles and connecting neighbouring particles using a straight line as shown in the figure.

Calculations Involving Unit Cell Dimensions:

X-Ray diffraction analysis is the most powerful tool for the determination of crystal structure. The inter planar distance (d) between two successive planes of atoms can be calculated using the following equation form the X-Ray diffraction data 2dsinθ = nλ

The above equation is known as Bragg’s equation.

Where

λ is the wavelength of X-ray used for diffraction.
θ is the angle of diffraction
n is the order of diffraction

By knowing the values of θ, λ and n we can calculate the value of d.

d = \(\frac{nλ}{2sinθ}\)

Using these values the edge length of the unit cell can be calculated.

Calculation of Density:

Using the edge length of a unit cell, we can calculate the density (ρ) of the crystal by considering a cubic unit cell as follows.

Equation (6) contains four variables namely ρ, n, M and a. If any three variables are known, the fourth one can be caluculated.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Classification of Crystalline Solids

The structural units of an ionic crystal are cations and anions. They are bound together by strong electrostatic attractive forces. To maximize the attractive force, cations are surrounded by as many anions as possible and vice versa. Ionic crystals possess definite crystal structure; many solids are cubic close packed. Example: The arrangement of Na⁺ and Cl^– ions in NaCl crystal.

Characteristics:

1. Ionic solids have high melting points.
2. These solids do not conduct electricity, because the ions are fixed in their lattice positions.
3. They do conduct electricity in molten state (or) when dissolved in water because, the ions are free to move in the molten state or solution.
4. They are hard as only strong external force can change the relative positions of ions.

Covalent Solids:

In covalent solids, the constituents (atoms) are bound together in a three dimensional network entirely by covalent bonds. Examples: Diamond, silicon carbide etc. Such covalent network crystals are very hard, and have high melting point. They are usually poor thermal and electrical conductors.

Molecular Solids:

In molecular solids, the constituents are neutral molecules. They are held together by weak vander Waals forces. Generally molecular solids are soft and they do not conduct electricity. These molecular solids are further classified into three types.

(i) Non-Polar Molecular Solids:

In non polar molecular solids constituent molecules are held together by weak dispersion forces or London forces. They have low melting points and are usually in liquids or gaseous state at room temperature. Examples: naphthalene, anthracene etc.,

(ii) Polar Molecular Solids

The constituents are molecules formed by polar covalent bonds. They are held together by relatively strong dipole-dipole interactions. They have higher melting points than the nonpolar molecular solids. Examples are solid CO₂, solid NH₃ etc.

(iii) Hydrogen Bonded Molecular Solids

The constituents are held together by hydrogen bonds. They are generally soft solids under room temperature. Examples: solid ice (H₂O), glucose, urea etc.,

Metallic Solids:

You have already studied in XI STD about the nature of metallic bonding. In metallic solids, the lattice points are occupied by positive metal ions and a cloud of electrons pervades the space. They are hard, and have high melting point. Metallic solids possess excellent electrical and thermal conductivity. They possess bright lustre. Examples: Metals and metal alloys belong to this type of solids, for example Cu, Fe, Zn, Ag, Au, CuZn etc.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Crystal Lattice and Unit Cell

Crystalline solid is characterised by a definite orientation of atoms, ions or molecules, relative to one another in a three dimensional pattern. The regular arrangement of these species throughout the crystal is called a crystal lattice. A basic repeating structural unit of a crystalline solid is called a unit cell. The following figure illustrates the lattice point and the unit cell.

A crystal may be considered to consist of large number of unit cells, each one in direct contact with its nearer neighbour and all similarly oriented in space. The number of nearest neighbours that surrounding a particle in a crystal is called the coordination number of that particle.

A unit cell is characterised by the three edge lengths or lattice constants a, b and c and the angle between the edges α, β and γ

The crystal lattice is the arrangement of the constituent particles like atoms, molecules, or ions in a three dimensional surface. On the other hand, the unit cell is known to be the building blocks of the crystal lattice, as they get repeated in three-dimensional space to yield shape to the crystal.

A unit cell is the smallest portion of a crystal lattice that shows the three-dimensional pattern of the entire crystal. A crystal can be thought of as the same unit cell repeated over and over in three dimensions.

The total three-dimensional arrangement of particles of a crystal is called the crystal structure. The actual arrangement of particles in the crystal is a lattice. The smallest part of a crystal that has the three dimensional pattern of the whole lattice is called a unit cell.

What is Crystal Lattice? The crystal lattice is the symmetrical three-dimensional structural arrangements of atoms, ions or molecules (constituent particle) inside a crystalline solid as points. It can be defined as the geometrical arrangement of the atoms, ions or molecules of the crystalline solid as points in space.

In total there are seven crystal systems: triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal, and cubic.

A lattice system is a class of lattices with the same set of lattice point groups, which are subgroups of the arithmetic crystal classes. The 14 Bravais lattices are grouped into seven lattice systems: triclinic, monoclinic, orthorhombic, tetragonal, rhombohedral, hexagonal, and cubic.

A lattice is a hypothetical regular and periodic arrangement of points in space. It is used to describe the structure of a crystal. A basis is a collection of atoms in particular fixed arrangement in space.

Lattice Points:

Point in a crystal with specific arrangement of atoms, reproduced many times in a macroscopic crystal. The choice of the lattice point within the unit cell is arbitrary.

Crystal Basis:

Arrangement of atoms within the unit cell.

There are four types of crystals:

1. Ionic
2. Metallic
3. Covalent network, and
4. Molecular

A lattice is an ordered array of points describing the arrangement of particles that form a crystal. The unit cell of a crystal is defined by the lattice points. For example, the image shown here is the unit cell of a primitive cubic structure. In the structure drawn, all of the particles (yellow) are the same.

The arrangement of atoms in a crystal. Each point represents one or more atoms in the actual crystal, and if the points are connected by lines, a crystal lattice is formed; the lattice is divided into a number of identical blocks, or unit cells, characteristic of the Bravais lattices.

Diamond is composed of carbon atoms stacked tightly together in a cubic crystal structure, making it a very strong material. This shows us that it is not only important to know what elements are in the mineral, but it is also very important to know how those elements are stacked together.

They are cubic, tetragonal, hexagonal (trigonal), orthorhombic, monoclinic, and triclinic. Seven-crystal system under their respective names, Bravias lattice.

A lattice is an abstract structure studied in the mathematical subdisciplines of order theory and abstract algebra. It consists of a partially ordered set in which every two elements have a unique supremum (also called a least upper bound or join) and a unique infinitum (also called a greatest lower bound or meet).

Crystals are composed of three-dimensional patterns. These patterns consist of atoms or groups of atoms in ordered and symmetrical arrangements which are repeated at regular intervals keeping the same orientation to one another.

A lattice is made by crisscrossing pieces of lath, thin strips of wood, at right angles. The small squares left open between the strips of wood create a gridlike, ornamental pattern. Panels of lattice often enclose other structures, such as a garden bench or gazebo.

The crystal structure is formed by associating every lattice point with an assembly of atoms or molecules or ions, which are identical in composition, arrangement and orientation, is called as the basis. The atomic arrangement in a crystal is called crystal structure.

A lattice point is a point at the intersection of two or more grid lines in a regularly spaced array of points, which is a point lattice. In a plane, point lattices can be constructed having unit cells in the shape of a square, rectangle, hexagon, and other shapes.

The definition of lattice is a structure made from wood or metal pieces arranged in a criss-cross or diamond pattern with spaces in between. A metal fence that is made up of pieces of metal arranged in criss-cross patterns with open air in between the pieces of metal is an example of lattice.

The most common and important are face-centred cubic (FCC) and hexagonal close-packed (HCP) structures. To get a clear picture of arrangements of atoms in these two crystal structures, it is necessary to examine the geometry of possible close-packing of atoms.

There are four types of crystals: covalent, ionic, metallic, and molecular. Each type has a different type of connection, or bond, between its atoms. The type of atoms and the arrangement of bonds dictate what type of crystal is formed.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Classification of Solids

We can classify solids into the following two major types based on the arrangement of their constituents.

• Crystalline solids
• Amorphous solids

The term crystal comes from the Greek word “krystallos” which means clear ice. This term was first applied to the transparent quartz stones, and then the name is used for solids bounded by many flat, symmetrically arranged faces.

A crystalline solid is one in which its constituents (atoms, ions or molecules), have an orderly arrangement extending over a long range. The arrangement of such constituents in a crystalline solid is such that the potential energy of the system is at minimum. In contrast, in amorphous solids (In Greek, amorphous means no form) the constituents are randomly arranged.

The following table shows the differences between crystalline and amorphous solids.

Crystalline Solids	Amorphous Solids
1. Long range orderly arrangement of constitutents	1. Short range, random arrangement of constituents
2. Definite shape	2. Irregular Shape
3. Generally crystalline solids are anisotropic in nature	3. They are isotropic like liquids
4. They are true solids	4. They are considered as pseudo solids (or) super cooled liquids
5. Definite Heat of fusion	5. Heat of fusion is not definite
6. They have sharp melting points	6. Gradually soften over a range of temperature and so can be moulded
7. Examples: Nacl, diamond etc.	7. Examples: Rubber, plastics, glass etc.

Isotropy

Isotropy means uniformity in all directions. In solid state isotropy means having identical values of physical properties such as refractive index, electrical conductance etc., in all directions, whereas anisotropy is the property which depends on the direction of measurement.

Crystalline solids are anisotropic and they show different values of physical properties when measured along different directions. The following figure illustrates the anisotropy in crystals due to different arrangement of their constituents along different directions.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

General Characteristics of Solids

We have already learnt in XI STD that gas molecules move randomly without exerting reasonable forces on one another. Unlike gases, in solids the atoms, ions or molecules are held together by strong force of attraction. The general characteristics of solids are as follows,

• Solids have definite volume and shape.
• Solids are rigid and incompressible
• Solids have strong cohesive forces.
• Solids have short inter atomic, ionic or molecular distances.
• Their constituents (atoms, ions or molecules) have fixed positions and can only oscillate about their mean positions.

solid have a fixed shape and a fixed volume, solid cannot be compressed solids have high density force of attraction between the particles is very strong. The space between the particles of solids is negligible.

Definite shape, definite volume, definite melting point, high density, incompressibility, and low rate of diffusion.

Solids have a definite mass, volume, and shape because strong intermolecular forces hold the constituent particles of matter together. The intermolecular force tends to dominate the thermal energy at low temperature and the solids stay in the fixed state. In a solid and liquid, the mass and volume remain the same.

Solids have many different properties, including conductivity, malleability, density, hardness, and optical transmission, to name a few.

A solid is a sample of matter that retains its shape and density when not confined. Examples of solids are common table salt, table sugar, water ice, frozen carbon dioxide (dry ice), glass, rock, most metals, and wood. When a solid is heated, the atoms or molecules gain kinetic energy.

Solids can be classified into two types: crystalline and amorphous. Crystalline solids are the most common type of solid. They are characterized by a regular crystalline organization of atoms that confer a long-range order. Amorphous, or non-crystalline, solids lack this long-range order.

The major types of solids are ionic, molecular, covalent, and metallic. Ionic solids consist of positively and negatively charged ions held together by electrostatic forces; the strength of the bonding is reflected in the lattice energy. Ionic solids tend to have high melting points and are rather hard.

The most obvious physical properties of a liquid are its retention of volume and its conformation to the shape of its container. When a liquid substance is poured into a vessel, it takes the shape of the vessel, and, as long as the substance stays in the liquid state, it will remain inside the vessel.

Some substances form crystalline solids consisting of particles in a very organized structure; others form amorphous (noncrystalline) solids with an internal structure that is not ordered. The main types of crystalline solids are ionic solids, metallic solids, covalent network solids, and molecular solids.

Mechanical Properties of solids describe characteristics such as their strength and resistance to deformation. Examples of mechanical properties are elasticity, plasticity, strength, abrasion, hardness, ductility, brittleness, malleability and toughness.

Solids like to hold their shape. In the same way that a large solid holds its shape, the atoms inside of a solid are not allowed to move around too much. Atoms and molecules in liquids and gases are bouncing and floating around, free to move where they want.

A solid is characterized by structural rigidity and resistance to a force applied to the surface. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire available volume like a gas.

Solids have definite shapes and definite volumes and are not compressible to any extent. There are two main categories of solids-crystalline solids and amorphous solids. Crystalline solids are those in which the atoms, ions, or molecules that make up the solid exist in a regular, well-defined arrangement.

In a solid, atoms and molecules are arranged in such a way that each molecule is acted upon by the forces due to the neighbouring molecules. These forces are known as inter molecular forces.

In crystalline solids, the atoms, ions or molecules are arranged in an ordered and symmetrical pattern that is repeated over the entire crystal. The smallest repeating structure of a solid is called a unit cell, which is like a brick in a wall. Unit cells combine to form a network called a crystal lattice.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Importance and Applications of Coordination Complexes

The coordination complexes are of great importance. These compounds are present in many plants, animals and in minerals. Some Important applications of coordination complexes are described below.

1. Phthalo blue – a bright blue pigment is a complex of Copper (II) ion and it is used in printing ink and in the packaging industry.

2. Purification of Nickel by Mond’s process involves formation [Ni(CO)₄], which Yields 99.5% pure Nickel on decomposition.

3. EDTA is used as a chelating ligand for the separation of lanthanides,in softning of hard water and also in removing lead poisoning.

4. Coordination complexes are used in the extraction of silver and gold from their ores by forming soluble cyano complex. These cyano complexes are reduced by zinc to yield metals. This process is called as Mac-Arthur-Forrest cyanide process.

5. Some metal ions are estimated more accurately by complex formation. For example, Ni²⁺ ions present in Nickel chloride solution is estimated accurately for forming an insoluble complex called [Ni(DMG)₂].

6. Many of the complexes are used as catalysts in organic and inorganic reactions. For example,

• Wilkinson’s catalyst – [(PPh₃)₃RhCl] is used for hydrogenation of alkenes.
• Ziegler-Natta catalyst – [TiCl₄] + Al(C₂H₅)₃ is used in the polymerization of ethene.

7. In order to get a fine and uniform deposit of superior metals (Ag, Au, Pt etc.,) over base metals, Coordination complexes [Ag(CN)₂]^– and [Au(CN)₂]^– etc., are used in electrolytic bath.

8. Many complexes are used as medicines for the treatment of various diseases. For example,

• Ca-EDTA chelate, is used in the treatment of lead and radioactive poisoning. That is for removing lead and radioactive metal ions from the body.
• Cis-platin is used as an antitumor drug in cancer treatment.

9. In photography, when the developed film is washed with sodium thio sulphatesolution (hypo), the negative film gets filed. Undecomposed AgBr forms a soluble complex called sodiumdithiosulphatoargentate (I) which can be easily removed by washing the film with water.

AgBr + 2 Na₂S₂O₃ → Na₃[Ag(S₂O₃)₂] + 2 NaBr

10. Many biological systems contain metal complexes. For example,

• A red blood corpuscles (RBC) is composed of heme group, which is Fe²⁺ – Porphyrin complex it plays an important role in carrying oxygen from lungs to tissues and carbon dioxide from tissues to lungs.
• Chlorophyll, a green pigment present in green plants and algae, is a coordination complex containing Mg²⁺ as central metal ion surrounded by a modified Porphyrin ligand called corrin ring.
• It plays an important role in photosynthesis, by which plants converts CO₂ and water into carbohydrates and oxygen.
• Vitamin B₁₂(cyanocobalamine) is the only vitamin consist of metal ion. it is a coordination complex in which the central metal ion is Co⁺ surrounded by Porphyrin like ligand.
• Many enzymes are known to be metal complexes, they regulate biological processes.
• For example, Carboxypeptidase is a protease enzyme that hydrolytic enzyme important in digestion, contains a zinc ion coordinated to the protein.

Find free online Chemistry Topics covering a broad range of concepts from research institutes around the world.

Stability of Metal Complexes

The stability of coordination complexes can be interpreted in two different ways. The first one is thermodynamic stability and second one is kinetic stability. Thermodynamic stability of a coordination complex refers to the free energy change (∆G) of a complex formation reaction. Kinetic stability of a coordination complex refers to the ligand substitution. In some cases, complexes can undergo rapid ligand substitution; such complexes are called labile complexes. However, some complexes undergo ligand substitution very slowly (or sometimes no substitution), such complexes are called inert complexes.

Stability Constant: (β)

The stability of a coordination complex is a measure of its resistance to the replacement of one ligand by another. The stability of a complex refers to the degree of association between two species involved in an equilibrium. Let us consider the following complex formation reaction

So, as the concentration of [Cu(NH₃)₄]²⁺ increases the value of stability complexes also increases. Therefore the greater the value of stability constant greater is the stability of the complex.

Generally coordination complexes are stable in their solutions; however, the complex ion can undergo dissociation to a small extent. Extent of dissociation depends on the strength of the metal ligand bond, thus Stronger the M ← L, lesser is the dissociation.

In aqueous solutions, when complex ion dissociates, there will be equilibrium between undissociated complex ion and dissociated ions. Hence the stability of the metal complex can be expressed in terms of dissociation equilibrium constant or instability constant (α). For example let us consider the dissociation of [Cu(NH₃)₄]²⁺ in aqueous solution.

[Cu(NH₃)₄]²⁺ ⇄ Cu²⁺ + 4NH₃

The dissociation equilibrium constant or instability constant is represented as follows,

From (1) and (2) we can say that, the reciprocal of dissociation equilibrium constant (α) is called as formation equilibrium constant or stability constant (β). β = (\(\frac{1}{α}\)).

Significance of Stability Constants

The stability of coordination complex is measured in terms of its stability constant (β). Higher the value of stability constant for a complex ion, greater is the stability of the complex ion. Stability constant values of some important complexes are listed in table

By comparing stability constant values in the above table, we can say that among the five complexes listed, [Hg(CN)₄]^2- is most stable complex ion and [Fe(SCN)]²⁺ is least stable.

Stepwise Formation Constants and Overall Formation Constants

When a free metal ion is in aqueous medium, it is surrounded by (coordinated with) water molecules. It is represented as [MS₆]. If ligands which are stronger than water are added to this metal salt solution, coordinated water molecules are replaced by strong ligands.

Let us consider the formation of a metal complex ML₆ in aqueous medium. (Charge on the metal ion is ignored) complex formation may occur in single step or step by step. If ligands added to the metal ion in single step, then

β_overall is called as overall stability constant. As solvent is present in large excess, its concentration in the above equation can be ignored.

If these six ligands are added to the metal ion one by one, then the formation of complex [ML₆] can be supposed to take place through six different steps as shown below. Generally step wise stability constants are represented by the symbol k.

In the above equilibrium, the values k₁, k₂, k₃, k₄, k₅ and k₆ are called step wise stability constants. By carrying out small a mathematical manipulation, we can show that overall stability constant β is the product of all step wise stability constants k₁, k₂, k₃, k₄, k₅ and k₆.
β = k₁ × k₂ × k₃ × k₄ × k₅ × k₆

On taking logarithm both sides
log(β) = log(k₁) + log(k₂) + log(k₃) + log(k₄) + log(k₅) + log(k₆).