Category: ICSE Class 10

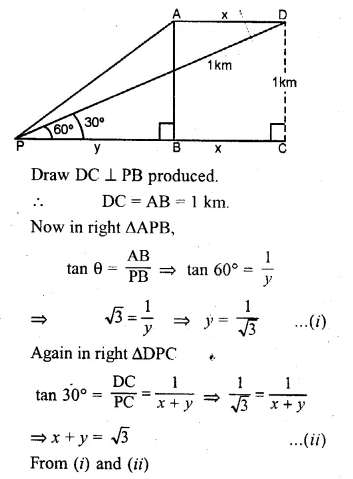
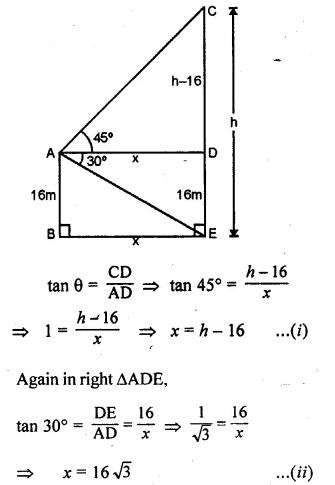
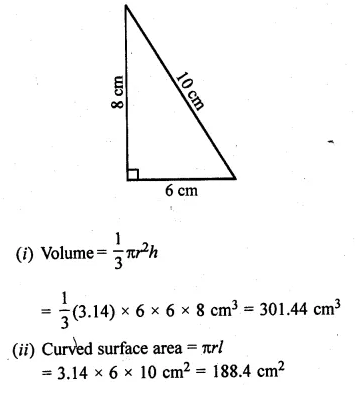
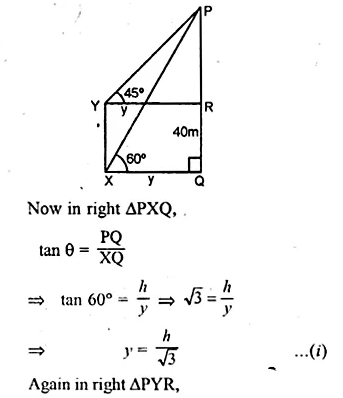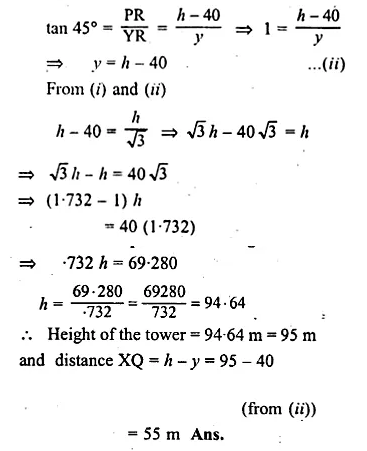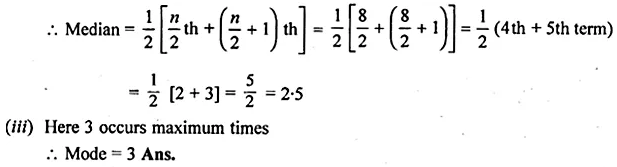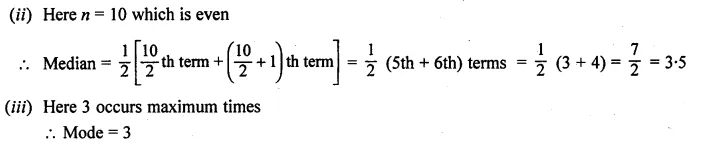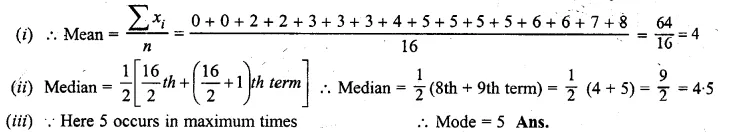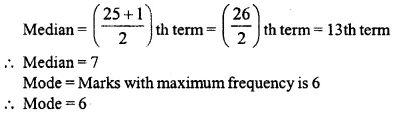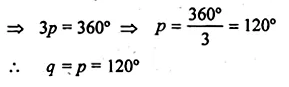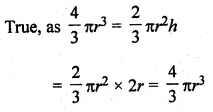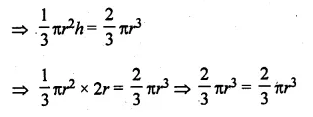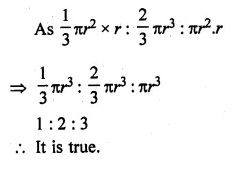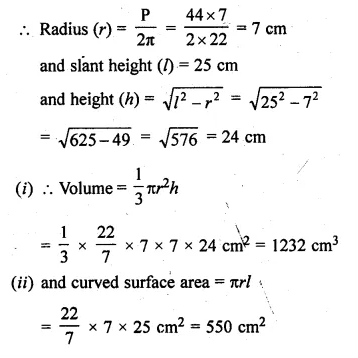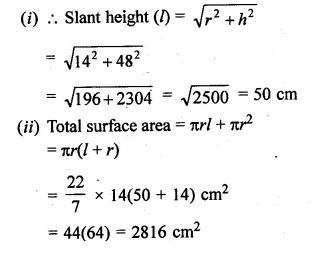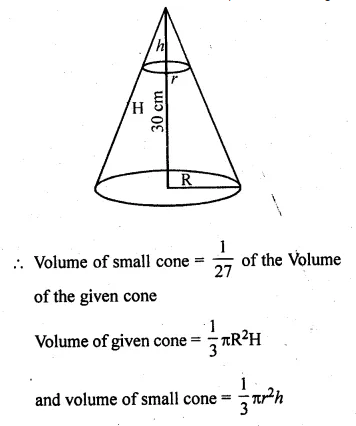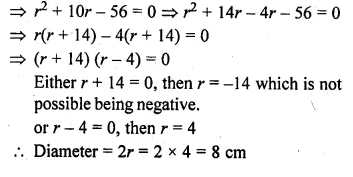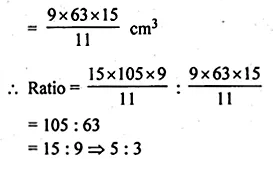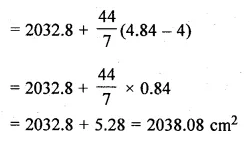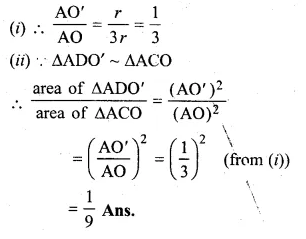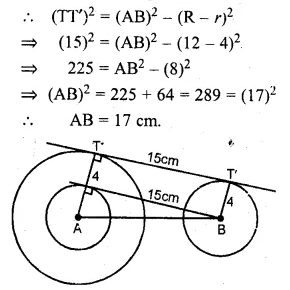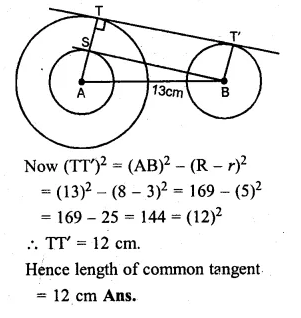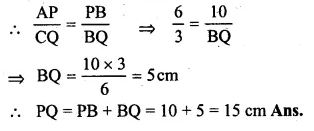ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test

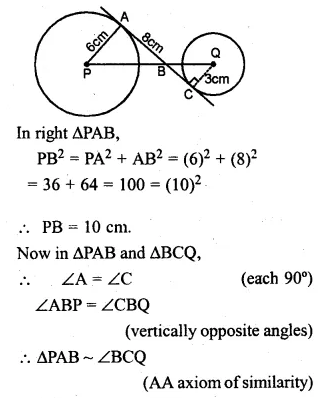
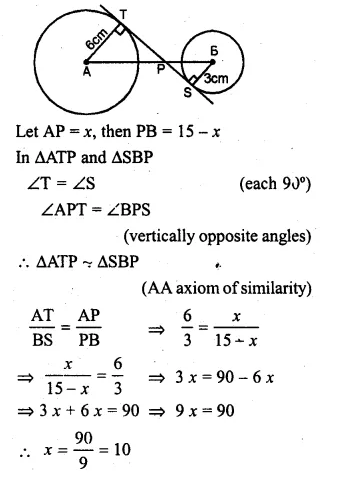
Question 1.
(a) Calculate the arithmetic mean of 5.7, 6.6, 7.2, 9.3, 6.2.
(b) The weights (in kg) of 8 new born babies are 3, 3.2, 3.4, 3.5, 4, 3.6, 4.1, 3.2. Find the mean weight of the babies.
Solution:
(a) Sum of 5 observations = 5.7 + 6.6 + 7.2 + 9.3 + 6.2 = 35.0
∴ Mean = \(\\ \frac { 35.0 }{ 5 } \) = 7
(b) Weights of 8 babies (in kg) are 3, 3.2, 3.4, 3.5, 4, 3.6, 4.1, 3.2
∴ Total weights of 8 babies
= 3 + 3.2 + 3.4 + 3.5 + 4 + 3.6 + 4.1 + 3.2 = 28.0 kg
Mean weight = \(\frac { \sum { { x }_{ i } } }{ n } \)
= \(\\ \frac { 28.0 }{ 8 } \) (Here n = 8)
= 3.5 kg

Question 2.
The marks obtained by 15 students in a class test are 12, 14, 07, 09, 23, 11, 08, 13, 11, 19, 16, 24, 17, 03, 20 find
(i) the mean of their marks.
(ii) the mean of their marks when the marks of each student are increased by 4.
(iii) the mean of their marks when 2 marks are deducted from the marks of each student.
(iv) the mean of their marks when the marks of each student are doubled.
Solution:
Sum of marks of 15 students.
= 12 + 14 + 07 + 09 + 23 + 11 + 08 + 13 + 11 + 19 + 16 + 24 + 17 + 03 + 20
= 207
(i) Mean = \(\\ \frac { 207 }{ 15 } \)
= 13.8

Question 3.
(a) The mean of the numbers 6, y, 7, x, 14 is 8. Express y in terms of x.
(b) The mean of 9 variates is 11. If eight of them are 7, 12, 9, 14, 21, 3, 8 and 15 find the 9th variate.
Solution:
(a) Sum of numbers = 6 + y + 7 + x + 14
= 27 + x + y …(i)
But mean of 5 numbers = 8
∴ Sum = 8 × 5 = 40 …(ii)
From (i) and (ii)
27 + x + y = 40
⇒ x + y = 40 – 27 = 13
∴ y = 13 – x
(b) Mean of 9 variates = 11
∴ Total sum =11 × 9 = 99
But sum of 8 of these variates
= 7 + 12 + 9 + 14 + 21 + 3 + 8 + 15 = 89
∴ 9th variate = 99 – 89 = 10

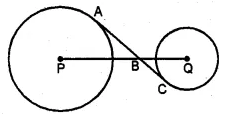
Question 4.
(a) The mean age of 33 students of a class is 13 years. If one girl leaves the class, the mean becomes \(12 \frac { 15 }{ 16 } \) years. What is the age of the girl ?
(b) In a class test, the mean of marks scored by a class of 40 students was calculated as 18.2. Later on, it was detected that marks of one student was wrongly copied as 21 instead of 29. Find the correct mean.
Solution:
(a) Mean age of 33 students = 13 years
Total age = 13 × 33 = 429 years
After leaving one girl, the mean of 32

Question 5.
Find the mean of 25 given numbers when the mean of 10 of them is 13 and the mean of the remaining numbers is 18.
Solution:
Mean of 10 numbers = 13
Sum = 13 × 10 = 130
and mean of remaining 15 numbers = 18
Sum = 18 × 15 = 270
Total sum of 25 numbers = 130 + 270 = 400
Mean of 25 numbers = \(\\ \frac { 400 }{ 25 } \) = 16

Question 6.
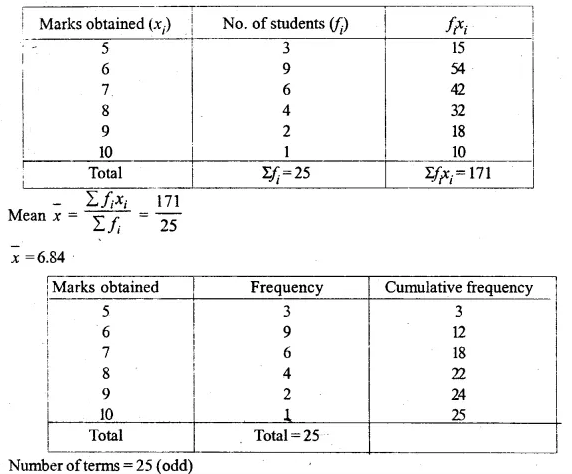
Find the mean of the following distribution:

Solution:

Question 7.
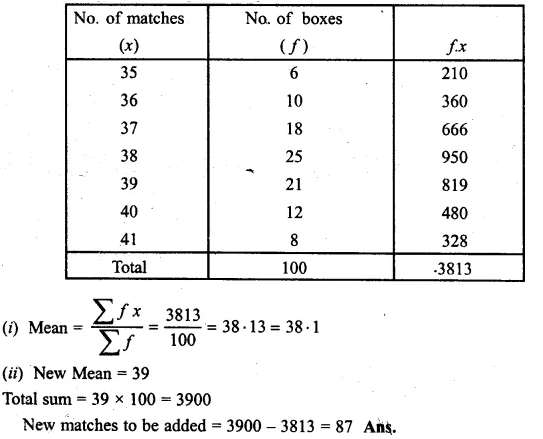
The contents of 100 match boxes were checked to determine the number of matches they contained

(i) Calculate, correct to one decimal place, the mean number of matches per box.
(ii) Determine how many extra matches would have to be added to the total contents of the 100 boxes to; bring the mean upto exactly 39 matches. (1997)
Solution:

Question 8.
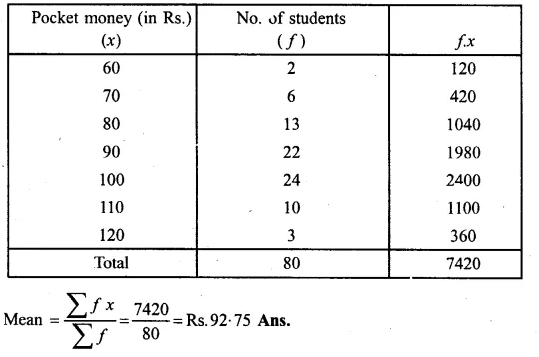
Calculate the mean for the following distribution :
>
Solution:

Question 9.
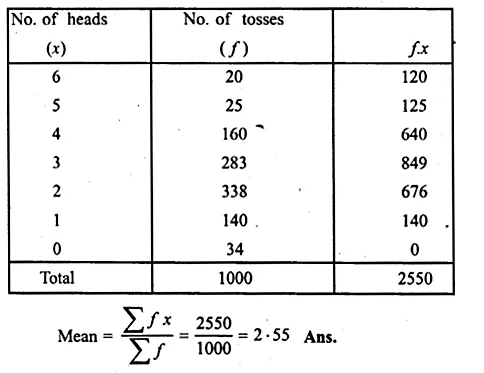
Six coins were tossed 1000 times, and at each toss the number of heads were counted and the results were recorded as under :

Calculate the mean for this distribution.
Solution:

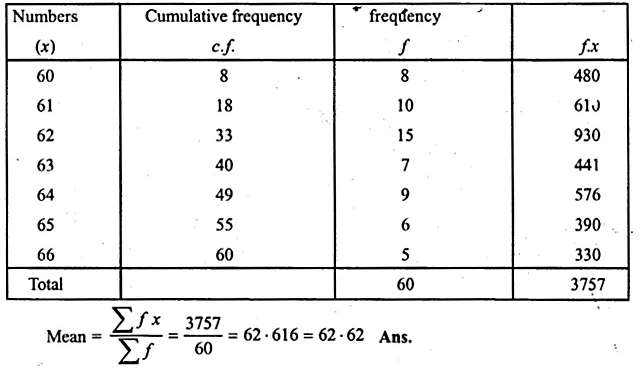
Question 10.
Find the mean for the following distribution

Solution:

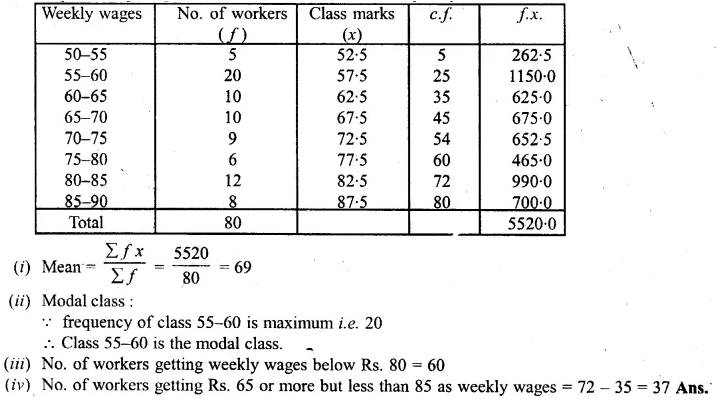
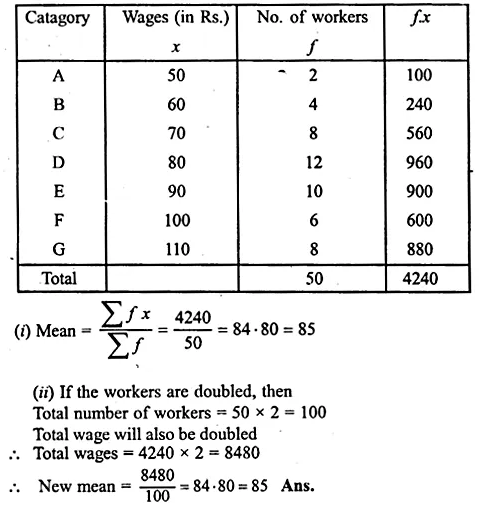
Question 11.

(i) Calculate the mean wage correct to the nearest rupee (1995)
(ii) If the number of workers in each category is doubled, what would be the new mean wage ?
Solution:

Question 12.
If the mean of the following distribution is 7.5, find the missing frequency ” f “.

Solution:

Question 13.
Find the value of the missing variate for the following distribution whose mean is 10

Solution:
Let missing variate be x, then

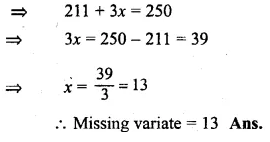
Question 14.
Marks obtained by 40 students in a short assessment are given below, where a and b are two missing data.

If the mean of the distribution is 7.2, find a and b.
Solution:

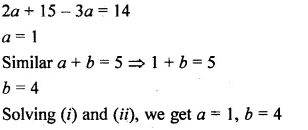
Question 15.
Find the mean of the following distribution

Solution:

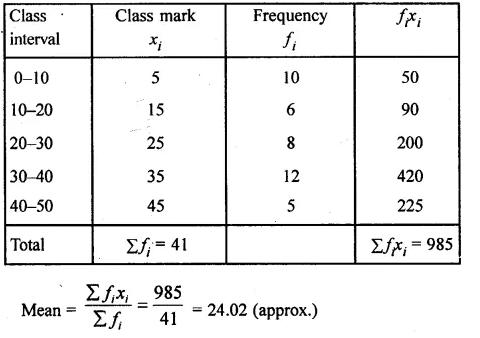
Question 16.
Calculate the mean of the following distribution:

Solution:
Consider the following distribution :

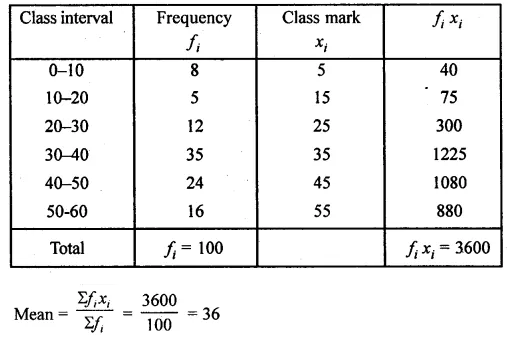
Question 17.
Calculate the mean of the following distribution using step deviation method:

Solution:

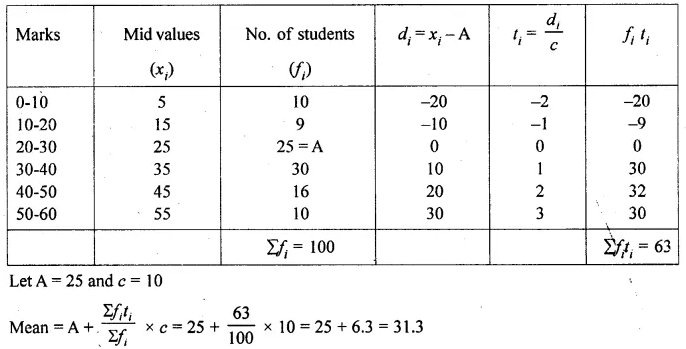
Question 18.
Find the mean of the following frequency distribution:

Solution:

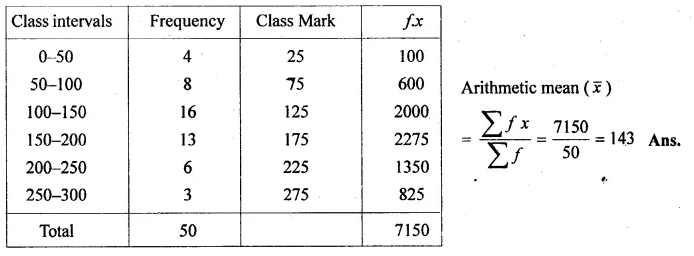
Question 19.
The following table gives the daily wages of workers in a factory:

Calculate their mean by short cut method.
Solution:

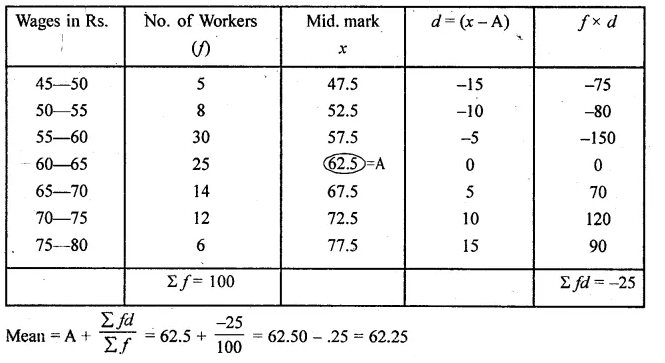
Question 20.
Calculate the mean of the distribution given below using the short cut method.

Solution:

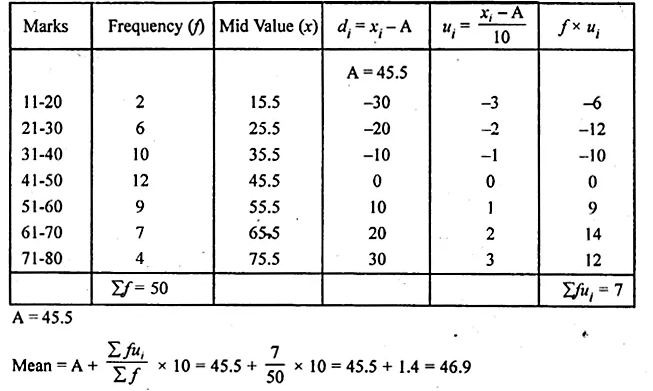
Question 21.
A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a students was absent.

Solution:

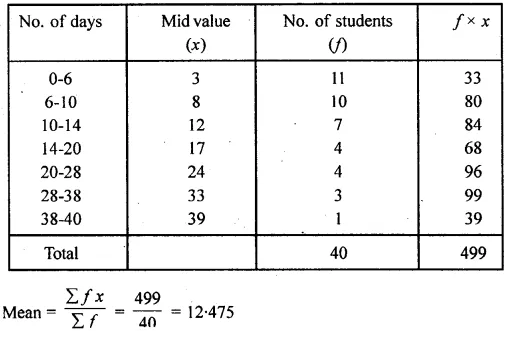
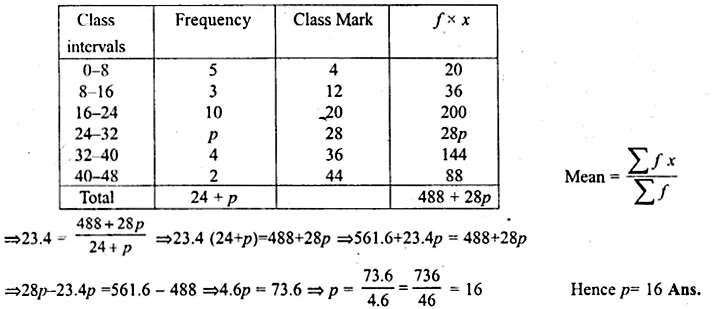
Question 22.
The mean of the following distribution is 23.4. Find the value of p.

Solution:

Question 23.
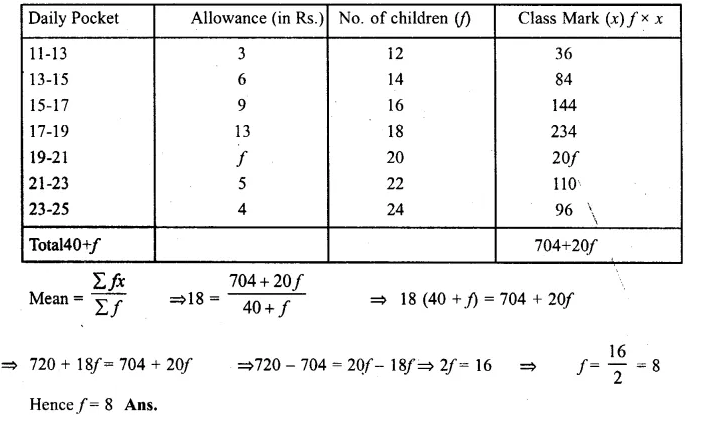
The following distribution shows the daily pocket allowance fo children of a locality. The mean pocket allowance is Rs. 18. Find the value of f

Solution:
Mean = Rs. 18

Question 24.
The mean of the following distribution is 50 and the sum of all the frequencies is 120. Find the values of p and q.

Solution:
Mean = 50, Total number of frequency = 120

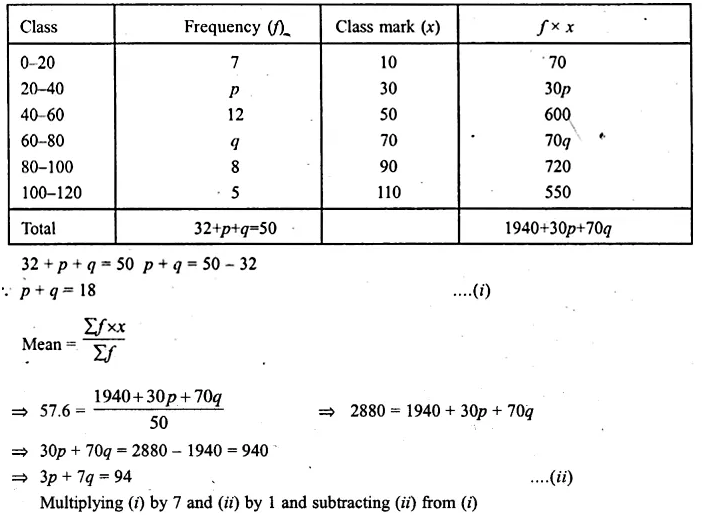
Question 25.
The mean of the following frequency distribution is 57.6 and the sum of all the frequencies is 50. Find the values of p and q.

Solution:
Mean = 57.6
and sum of all frequencies = 50

Question 26.
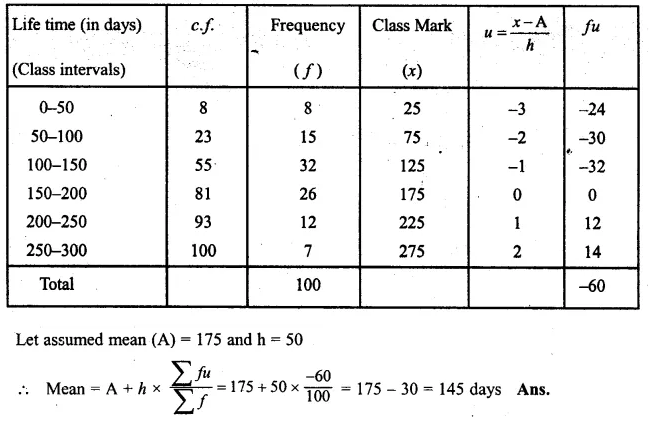
The following table gives the life time in days of 100 electricity tubes of a certain make :

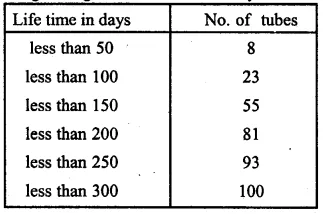
Find the mean life time of electricity tubes.
Solution:

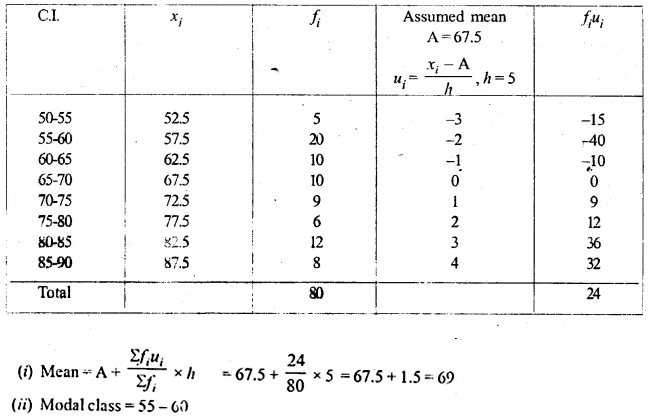
Question 27.
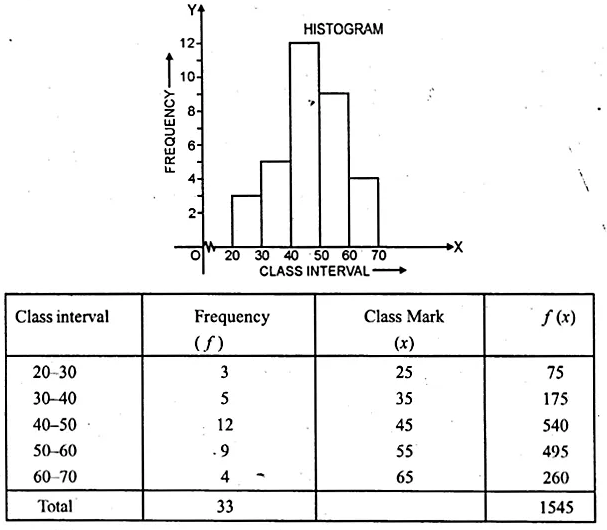
Using the information given in the adjoining histogram, calculate the mean correct to one decimal place.
Solution:
From the histogram given, we represent the information in the following table :

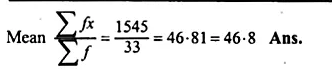
We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances Ex 20
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances Chapter Test

Question 1.
The angle of elevation of the top of a tower from a point A (on the ground) is 30°. On walking 50 m towards the tower, the angle of elevation is found to be 60°. Calculate
(i) the height of the tower (correct to one decimal place).
(ii) the distance of the tower from A.
Solution:
Let TR be the tower and A is a point on the ground
and angle of elevation of the top of tower = 30°
AB = 50 m
and from B, the angle of elevation is 60°
Let TR = h and AR = x
BR = x – 50

Question 2.
An aeroplane 3000 m high passes vertically above another aeroplane at an instant when the angles of elevation of the two aeroplanes from the same point on the ground are 60° and 45° respectively. Find the vertical distance between the two planes.
Solution:
Let A and B are two aeroplanes
and P is a point on the ground such that
angles of elevations from A and B are 60° and 45° respectively.
AC = 3000 m
Let AB = x
∴ BC = 3000 – x
Let PC = y

Question 3.
A 7m long flagstaff is fixed on the top of a tower. From a point on the ground, the angles of elevation of the top and bottom of the flagstaff are 45° and 36° respectively. Find the height of the tower correct to one place of demical.
Solution:
Let TR be the tower and PT is the flag on it such that PT = 7m
Let TR = h and AR = x
Angles of elevation from P and T are 45° and 36° respectively.
Now in right ∆PAR

Question 4.
A boy 1.6 m tall is 20 m away from a tower and observes that the angle of elevation of the top of the tower is 60°. Find the height of the tower.
Solution:
Let AB be the boy and TR be the tower
∴ AB = 1.6 m
Let TR = h
from A, show AE || BR
∴ ER = AB = 1.6 m
TE = h – 1.6
AE = BR = 20 m

h = 36.24
∴ Height of tower = 36.24 m

Question 5.
A boy 1.54 m tall can just see the sun over a wall 3.64 m high which is 2.1 m away from him. Find the angle of elevation of the sun.
Solution:
Let AB be the boy and CD be the wall which is at a distance of 2.1 m

Question 6.
In the adjoining figure, the angle of elevation of the top P of a vertical tower from a point X is 60° ; at a point Y, 40 m vertically above X, the angle of elevation is 45°. Find
(i) the height of the tower PQ
(ii) the distance XQ
(Give your answer to the nearest metre)

Solution:
Let PQ be the tower and let PQ = h
and XQ = YR = y
XY = 40 m
∴ PR = h – 40

Question 7.
An aeroplane is flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
Solution:
A and D are the two positions of the aeroplane ;
AB is the height and P is the point
∴ AB = 1 km,
Let AD = x and PB = y
and angles of elevation from A and D at point P are 60° and 30° respectively.

Question 8.
A man on the deck of a ship is 16 m above the water level. He observes that the angle of elevation of the top of a cliff is 45° and the angle of depression of the base is 30°. Calculate the distance of the cliff from the ship and the height of the cliff.
Solution:
Let A is the man on the deck of a ship B and CE is the cliff.
AB = 16 m and angle of elevation from the top of the cliff in 45°
and the angle of depression at the base of the cliff is 30°.
Let CE = h, AD = x, then
CD = h – 16, AD = BE = x
Now in right ∆CAD

Question 9.
There is a small island in between a river 100 metres wide. A tall tree stands on the island. P and Q are points directly opposite to each other on the two banks and in the line with the tree. If the angles of elevation of the top of the tree from P and Q are 30° and 45° respectively, find the height of the tree.
Solution:
The width of the river (PQ) = 100 m.
B is the island and AB is the tree on it.

Question 10.
A man standing on the deck of the ship which is 20 m above the sea-level, observes the angle of elevation of a bird as 30° and the angle of depression of its reflection in the sea as 60°. Find the height of the bird
Solution:
Let P is the man standing on the deck of a ship
which is 20 m above the sea level and B is the bird.
Now angle of elevation of the bird from P = 30°
and angle of depression from P to the shadow of the bird in the sea

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances Chapter Test help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances Chapter Test, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.6
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Chapter Test

Question 1.
Find the mode of the following sets of numbers ;
(i) 3, 2, 0, 1, 2, 3, 5, 3
(ii) 5, 7, 6, 8, 9, 0, 6, 8, 1, 8
(iii) 9, 0, 2, 8, 5, 3, 5, 4, 1, 5, 2, 7
Solution:
(i) ∵ The number 3 occurs maximum times
Mode = 3
(ii) ∵ The number 8 occurs maximum times
Mode = 8
(iii) ∵ The number 5, occurs maximum times
Mode = 5

Question 2.
Calculate the mean, the median and the mode of the numbers : 3, 2, 6, 3, 3, 1, 1, 2
Solution:
Arranging in ascending order 1, 1, 2, 2, 3, 3, 3, 6
(i) Mean = \(\frac { \sum { { x }_{ i } } }{ n } \)
= \(\frac { 1+1+2+2+3+3+3+6 }{ 8 } \)
= \(\\ \frac { 21 }{ 8 } \)
= 2.625
(ii) Here n = 8 which is even

Question 3.
Find the mean, median and mode of the following distribution : 8, 10, 7, 6, 10, 11, 6, 13, 10
Solution:
Mean = \(\\ \frac { 8+10+7+6+10+11+6+13+10 }{ 2 } \)
= \(\\ \frac { 81 }{ 9 } \) = 9
Given nos. in ascending order are as follows:
6, 6, 7, 8, 10, 10, 10, 11, 13
Median = \(\\ \frac { n+1 }{ 2 } \) th term = \(\\ \frac { 9+1 }{ 2 } \) = 5th term = 10
Mode = 10 (having highest frequency 3 times)

Question 4.
Calculate the mean, the median and the mode of the following numbers : 3, 1, 5, 6, 3, 4, 5, 3, 7, 2
Solution:
Arranging in ascending order 1, 2, 3, 3, 3, 4, 5, 5, 6, 7
(i) Mean = \(\frac { \sum { { x }_{ i } } }{ n } \)
= \(\frac { 1+2+3+3+3+4+5+5+6+7 }{ 8 } \)
= \(\\ \frac { 39 }{ 10 } \)
= 3.9

Question 5.
The marks of 10 students of a class in an examination arranged in ascending order are as follows: 13, 35, 43, 46, x, x +4, 55, 61,71, 80
If the median marks is 48, find the value of x. Hence, find the mode of the given data. (2017)
Solution:
Given marks are 13, 35, 43, 46, x, x + 4, 55, 61, 71, 80
n = 10 (even), median = 48

Question 6.
A boy scored the following marks in various class tests during a term each test being marked out of 20: 15, 17, 16, 7, 10, 12, 14, 16, 19, 12, 16
(i) What are his modal marks ?
(ii) What are his median marks ?
(iii) What are his mean marks ?
Solution:
Arranging in ascending order 7, 10, 12, 12, 14, 15, 16, 16, 16, 17, 19
(ii) Here n = 11 which is odd

Question 7.
Find the mean, median and mode of the following marks obtained by 16 students in a class test marked out of 10 marks : 0, 0, 2, 2, 3, 3, 3, 4, 5, 5, 5, 5, 6, 6, 7, 8
Solution:
Here, n = 16

Question 8.
Find the mode and median of the following frequency distribution :

Solution:

Question 9.
The marks obtained by 30 students in a class assessment of 5 marks is given below:

Calculate the mean, median and mode of the above distribution.
Solution:

Question 10.
The distribution given below shows the marks obtained by 25 students in an aptitude test. Find the mean, median and mode of the distribution.

Solution:

Question 11.
At a shooting competition, the scores of a competitor were as given below :

(i) What was his modal score ?
(ii) What was his median score ?
(iii) What was his total score ?
(iv) What was his mean ?
Solution:
Writing the given distribution in cumulative frequency distribution:

Question 12.
(i) Using step-deviation method, calculate the mean marks of the following distribution.
(ii) State the modal class.

Solution:

Question 13.
The following table gives the weekly wages (in Rs.) of workers in a factory :

Calculate:
(i) The mean.
(ii) the modal class
(iii) the number of workers getting weekly wages below Rs. 80.
(iv) the number of workers getting Rs. 65 or more but less than Rs. 85 as weekly wages.
Solution:
Representing the given distribution in cumulative frequency distribution

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 21 Measures of Central Tendency Ex 21.3, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances Ex 20
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances Chapter Test

Choose the correct answer from the given four options (1 to 9):

Question 1.
In the given figure, the length of BC is
(a) 2 √3 cm
(b) 3 √3 km
(c) 4 √3 cm
(d) 3 cm

Solution:
In the given figure, \(\\ \frac { BC }{ AC } \) = sin 30°
⇒ \(\\ \frac { BC }{ 6 } \) = \(\\ \frac { 1 }{ 2 } \)
⇒ BC = \(\\ \frac { 6 }{ 2 } \) = 3cm (d)

Question 2.
In the given figure, if the angle of elevation is 60° and the distance AB = 10 √3 m, then the height of the tower is
(a) 20 √3 cm
(b) 10 m
(c) 30 m
(d) 30 √3 m

Solution:
In the given figure,
∠A = 60°, AB = 10 √3 m
Let BC = h
tan 60° = \(\frac { h }{ 10\sqrt { 3 } } \)
⇒ \(\sqrt { 3 } =\frac { h }{ 10\sqrt { 3 } } \)
⇒ h = 10 √3 × √3 = 10 × 3 = 30 m (c)

Question 3.
If a kite is flying at a height of 40 √3 metres from the level-ground, attached to a string inclined at 60° to the horizontal, then the length of the string is
(a) 80 m
(b) 60 √3 m
(c) 80 √3 m
(d) 120 m
Solution:
Let K is kite
Height of KT = 40 √3 m
Angle of elevation of string at the ground = 60°
Let length of string AK = x m

Question 4.
The top of a broken tree has its top touching the ground (shown in the given figure) at a distance of 10 m from the bottom. If the angle made by the broken part with ground is 30°, then the length of the broken part is
(a) 10 √3 m
(b) \(\frac { 20 }{ \sqrt { 3 } } \)
(c) 20 m
(d) 20 √3 m

Solution:
From the figure, AC is the height of tree and from B, it was broken
AB = A’C
Angle of elevation = 30°
A’C = 10 m
Let AC = hm’
and A’B = x m
BC = h – x m
\(cos\theta =\frac { A’C }{ A’B } \)
\(cos{ 30 }^{ o }=\frac { 10 }{ x } \)

Question 5.
If the angle of depression of an object from a 75 m high tower is 30°, then the distance of the object from the tower is
(a) 25 √3 m
(b) 50√ 3 m
(c) 75 √3 m
(d) 150 m
Solution:
Height tower AB = 75 m
C is an object on the ground and angle of depression from A is 30°.

Question 6.
A ladder 14 m long rests against a wall. If the foot of the ladder is 7 m from the wall, then the angle of elevation is
(a) 15°
(b) 30°
(c) 45°
(d) 60°
Solution:
Length of a ladder AB = 14 m

Question 7.
If a pole 6 m high casts shadow 2 √3 m long on the ground, then the sun’s elevation is
(a) 60°
(b) 45°
(c) 30°
(d) 90°
Solution:
Height of pole AB = 6 m
and its shadow BC = 2√3 m

Question 8.
If the length of the shadow of a tower is √3 times that of its height, then the angle of elevation of the sun is
(a) 15°
(b) 30°
(c) 45°
(d) 60°
Solution:
Let height of a tower AB = h m
Then its shadow BC = √3 hm

Question 9.
In ∆ABC, ∠A = 30° and ∠B = 90°. If AC = 8 cm, then its area is
(a) 16 √3 cm²
(b) 16 m²
(c) 8 √3 cm²
(d) 6 √3 cm²
Solution:
In ∆ABC, ∠A = 30°, ∠B = 90°
AC = 8 cm

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances MCQS help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 20 Heights and Distances MCQS, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Chapter Test

Question 1.
Using the given information, find the value of x in each of the following figures :


Solution:
(i) ∠ADB and ∠ACB are in the same segment.
∠ADB = ∠ACB = 50°
Now in ∆ADB,
∠DAB + X + ∠ADB = 180°

Question 2.
If O is the centre of the circle, find the value of x in each of the following figures (using the given information):


Solution:
(i) ∠ACB = ∠ADB
(Angles in the same segment of a circle)
But ∠ADB = x°

Question 3.
(a) In the figure (i) given below, AD || BC. If ∠ACB = 35°. Find the measurement of ∠DBC.
(b) In the figure (ii) given below, it is given that O is the centre of the circle and ∠AOC = 130°. Find∠ABC

Solution:
(a) Construction: Join AB
∠A = ∠C = 35° [∵ Alt angles]

Question 4.
(a) In the figure (i) given below, calculate the values of x and y.
(b) In the figure (ii) given below, O is the centre of the circle. Calculate the values of x and y.

Solution:
(a) ABCD is a cyclic quadrilateral

Question 5.
(a) In the figure (i) given below, M, A, B, N are points on a circle having centre O. AN and MB cut at Y. If ∠NYB = 50° and ∠YNB = 20°, find ∠MAN and the reflex angle MON.
(b) In the figrue (ii) given below, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°, find
(i) ∠ACB
(ii) ∠OBC
(iii) ∠OAB
(iv) ∠CBA

Solution:
(a) ∠NYB = 50°, ∠YNB = 20°.

Question 6.
(a) In the figure (i) given below, O is the centre of the circle and ∠PBA = 42°. Calculate the value of ∠PQB
(b) In the figure (ii) given below, AB is a diameter of the circle whose centre is O. Given that ∠ECD = ∠EDC = 32°, calculate
(i) ∠CEF
(ii) ∠COF.

Solution:
(a) In ∆APB,
∠APB = 90° (Angle in a semi-circle)
But ∠A + ∠APB + ∠ABP = 180° (Angles of a triangle)
∠A + 90° + 42°= 180°
∠A + 132° = 180°
⇒ ∠A = 180° – 132° = 48°
But ∠A = ∠PQB

Question 7.
(a) In the figure (i) given below, AB is a diameter of the circle APBR. APQ and RBQ are straight lines, ∠A = 35°, ∠Q = 25°. Find (i) ∠PRB (ii) ∠PBR (iii) ∠BPR.
(b) In the figure (ii) given below, it is given that ∠ABC = 40° and AD is a diameter of the circle. Calculate ∠DAC.

Solution:
(a) (i) ∠PRB = ∠BAP
(Angles in the same segment of the circle)
∴ ∠PRB = 35° (∵ ∠BAP = 35° given)
(ii) In ∆PRQ,

Question 8.
(a) In the figure given below, P and Q are centres of two circles intersecting at B and C. ACD is a st. line. Calculate the numerical value of x.

(b) In the figure given below, O is the circumcentre of triangle ABC in which AC = BC. Given that ∠ACB = 56°, calculate
(i)∠CAB
(ii)∠OAC

Solution:
Given that
(a) Arc AB subtends ∠APB at the centre
and ∠ACB at the remaining part of the circle

Question 9.
(a) In the figure (i) given below, chord ED is parallel to the diameter AC of the circle. Given ∠CBE = 65°, calculate ∠DEC.

(b) In the figure (ii) given below, C is a point on the minor arc AB of the circle with centre O. Given ∠ACB = p°, ∠AOB = q°, express q in terms of p. Calculate p if OACB is a parallelogram.
Solution:
(a) ∠CBE = ∠CAE
(Angle in the same segment of a circle)
⇒ ∠CAE = 65°
∠AEC = 90° (Angle in a semi circle)
Now in ∆AEC
∠AEC + ∠CAE + ∠ACE = 180° (Angle of a triangle)
⇒ 90°+ 65° +∠ACE = 180°
⇒ 155° + ∠ACE = 180°
⇒ ∠ACE = 180° – 155° – 25°
∵AC || ED (given)
∴∠ACE = ∠DEC (alternate angles)
∴∠DEC = 25°

Question 10.
(a) In the figure (i) given below, straight lines AB and CD pass through the centre O of a circle. If ∠OCE = 40° and ∠AOD = 75°, find the number of degrees in :
(i) ∠CDE
(ii) ∠OBE.
(b) In the figure (ii) given below, I is the incentre of ∆ABC. AI produced meets the circumcircle of ∆ABC at D. Given that ∠ABC = 55° and ∠ACB = 65°, calculate
(i) ∠BCD
(ii) ∠CBD
(iii) ∠DCI
(iv) ∠BIC.

Solution:
(a) (i) ∠CED = 90° (Angle in semi-circle)
In ∆CED
∠CED + ∠CDE + ∠DCE = 180°
⇒ 90° +∠CDE + 40° = 180°
⇒ 130° + ∠CDE = 180°
⇒ ∠CDE = 180° – 130° = 50°

NCVT MIS 2019

Question 11.
O is the circumcentre of the triangle ABC and D is mid-point of the base BC. Prove that ∠BOD = ∠A.
Solution:
In the given figure, O is the centre of circumcentre of ∆ABC.
D is mid-point of BC. BO, CO and OD are joined.

Question 12.
In the given figure, AB and CD are equal chords. AD and BC intersect at E. Prove that AE = CE and BE = DE.

Solution:
In the given figure, AB and CD are two equal chords
AD and BC intersect each other at E.
To prove : AE = CE and BE = DE
Proof:
In ∆AEB and ∆CED
AB = CD (given)
∠A = ∠C (angles in the same segment)
∠B = ∠D (angles in the same segment)
∴ ∆AEB ≅ ∆CED (ASA axiom)
∴ AE = CE and BE = DE (c.p.c.t.)

Question 13.
(a) In the figure (i) given below, AB is a diameter of a circle with centre O. AC and BD are perpendiculars on a line PQ. BD meets the circle at E. Prove that AC = ED.
(b) In the figure (ii) given below, O is the centre of a circle. Chord CD is parallel to the diameter AB. If ∠ABC = 25°, calculate ∠CED.

Solution:
(a) Given: AB is the diameter of a circle with centre O.
AC and BD are perpendiculars on a line PQ,
such that BD meets the circle at E.

Question 14.
In the adjoining figure, O is the centre of the given circle and OABC is a parallelogram. BC is produced to meet the circle at D.
Prove that ∠ABC = 2 ∠OAD.

Solution:
Given: In the figure,
OABC is a || gm and O is the centre of the circle.
BC is produced to meet the circle at D.
To Prove : ∠ABC = 2∠OAD.
Construction: Join AD.

Question 15.
(a) In the figure (i) given below, P is the point of intersection of the chords BC and AQ such that AB = AP. Prove that CP = CQ.

(b) In the figure (i) given below, AB = AC = CD, ∠ADC = 38°. Calculate :
(i) ∠ABC (ii) ∠BEC.

Solution:
(a) Given: Two chords AQ and BC intersect each other at P
inside the circle. AB and CQ are joined and AB = AP.
To Prove : CP = CQ
Construction : Join AC.
Proof: In ∆ABP and ∆CQP
∴ ∠B = ∠Q

Question 16.
(a) In the figure (i) given below, CP bisects ∠ACB. Prove that DP bisects ∠ADB.
(b) In the figure (ii) given below, BDbisects ∠ABC. Prove that \(\frac { AB }{ BD } =\frac { BE }{ BC } \)

Solution:
(a)Given: In the figure, CP is the bisector of
∠ACB meeting the circle at P.
PD is joined

Question 17.
(a) In the figure (ii) given below, chords AB and CD of a circle intersect at E.
(i) Prove that triangles ADE and CBE are similar.
(ii) Given DC =12 cm, DE = 4 cm and AE = 16 cm, calculate the length of BE.

(b) In the figure (ii) given below, AB and CD are two intersecting chords of a circle. Name two triangles which are similar. Hence, calculate CP given that AP = 6cm, PB = 4 cm, and CD = 14 cm (PC > PD).

Solution:
(a) Given: Two chords AB and CD intersect each other
at E inside the circle.

Question 18.
In the adjoining figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find DE. (2008)

Solution:
In the figure, AE and BC intersect each other at D.
AB is joined.

Question 19.
(a) In the figure (i) given below, PR is a diameter of the circle, PQ = 7 cm, QR = 6 cm and RS = 2 cm. Calculate the perimeter of the cyclic quadrilateral PQRS.
(b) In the figure (ii) given below, the diagonals of a cyclic quadrilateral ABCD intersect in P and the area of the triangle APB is 24 cm². If AB = 8 cm and CD = 5 cm, calculate the area of ∆DPC.

Solution:
(a) PR is the diameter of the circle
PQ = 7 cm, QR = 6 cm, RS = 2 cm.

Question 20.
(a) In the figure (i) given below, QPX is the bisector of ∠YXZ of the triangle XYZ. Prove that XY : XQ = XP : XZ,
(b) In the figure (ii) given below, chords BA and DC of a circle meet at P. Prove that:
(i) ∠PAD = ∠PCB
(ii) PA. PB = PC . PD.

Solution:
(a) Given: ∆XYZ is inscribed in a circle.
Bisector of ∠YXZ meets the circle at Q.
QY is joined.
To Prove : XY : XQ = XP : XZ

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.1 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.1, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Ex 14
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Chapter Test

Question 1.
Draw a straight line AB of length 8 cm. Draw the locus of all points which are equidistant from A and B. Prove your statement.
Solution:
(i) Draw a line segment AB = 8 cm.

(ii) Draw the perpendicular bisector of AB intersecting AB at D.
∴ Every point P on it will be equidistant from A and B.
(iii) Take a point P on the perpendicular bisector.
(iv) Join PA and PB.
Proof: In ∆PAD and ∆PBD
PD = PD (common)
AD = BD (D is mid-point of AB)
∠PDA = ∠PDB (each 90°)
∴ ∆ PAD ≅ ∆ PBD (SAS axiom of congruency)
∴PA = PB (c.p.c.t.)
Similarly, we can prove any other point on the
perpendicular bisector of AB is equidistant from A and B.
Hence Proved.

Question 2.
A point P is allowed to travel in space. State the locus of P so that it always remains at a constant distance from a fixed point C.
Solution:
The point P is moving in the space and
it is at a constant distance from a fixed point C.
∴ Its locus is a sphere.

Question 3.
Draw a line segment AB of length 7 cm. Construct the locus of a point P such that area of triangle PAB is 14 cm².
Solution:
Base of ∆PAB = 7 cm
and its area = 14 cm²

Now draw a line XY parallel to AB at a distance of 4 cm.
Now take any point P on XY
Join PA and PB
area of ∆PAB = 14 cm.
Hence locus of P is the line XY
which is parallel to AB at a distance of 4 cm.

Question 4.
Draw a line segment AB of length 12 cm. Mark M, the mid-point of AB. Draw and describe the locus of a point which is
(i) at a distance of 3 cm from AB.
(ii) at a distance of 5 cm from the point M. Mark the points P, Q, R, S which satisfy both the above conditions. What kind of quadrilateral is PQRS? Compute the area of the quadrilateral PQRS.
Solution:
Steps of Construction :

(i) Take a line AB = 12 cm
(ii) Take M, the midpoint of AB.
(iii) Draw straight lines CD and EF parallel to AB at a distance of 3 cm.
(iv) With centre M and radius 5 cm,
draw areas which intersect CD at P and Q and EF at R and S.
(v) Join QR and PS.
PQRS is a rectangle where the length PQ = 8 cm.
Area of rectangle PQRS = PQ x RS = 8 x 6 = 48 cm²

Question 5.
AB and CD are two intersecting lines. Find the position of a point which is at a distance of 2 cm from AB and 1.6 cm from CD.
Solution:
(i) AB and CD are the intersecting lines which intersect each other at O.

(ii) Draw a line EF parallel to AB and GH parallel to CD intersecting each other at P
P is the required point.

Question 6.
Two straight lines PQ and PK cross each other at P at an angle of 75°. S is a stone on the road PQ, 800 m from P towards Q. By drawing a figure to scale 1 cm = 100 m, locate the position of a flagstaff X, which is equidistant from P and S, and is also equidistant from the road.
Solution:
1 cm = 100 cm
800 m = 8 cm.
Steps of Construction :
(i) Draw the lines PQ and PK intersecting each other
at P making an angle of 75°.

(ii) Take a point S on PQ such that PS = 8 cm.
(iii) Draw the perpendicular bisector of PS.
(iv) Draw the angle bisector of ∠KPS intersecting
the perpendicular bisector at X.
X is the required point which is equidistant from P and S
and also from PQ and PK.

Question 7.
Construct a rhombus PQRS whose diagonals PR, QS are 8 cm and 6 cm respectively. Find by construction a point X equidistant from PQ, PS and equidistant from R, S. Measure XR.
Solution:
Steps of Construction :

(i) Take PR = 8 cm and draw the perpendicular bisector
of PR intersecting it at O.
(ii) From O, out. off OS = OQ = 3 cm
(iii) Join PQ, QR, RS and SP.
PQRS is a rhombus. Whose diagonal are PR and QS.
(iv) PR is the bisector of ∠SPQ.
(v) Draw the perpendicular bisector of SR intersecting PR at X
∴ X is equidistant from PQ and PS and also from S and R.
On measuring length of XR = 3.2 cm (approx)

Question 8.
Without using set square or protractor, construct the parallelogram ABCD in which AB = 5.1 cm. the diagonal AC = 5.6 cm and the diagonal BD = 7 cm. Locate the point P on DC, which is equidistant from AB and BC.
Solution:
Steps of Construction :

(i) Take AB = 5.1 cm
(ii) At A, with readius \(\\ \frac { 5.6 }{ 2 } \) = 2.8 cm
and at B with radius \(\\ \frac { 7.0 }{ 2 } \) = 3.5 cm,
draw two arcs intersecting each other at O.
(iii) Join AO and produce it to C such that
OC = AD = 2.8 cm and
join BO and produce it to D such that
BO = OD = 3.5 cm
(iv) Join BC, CD, DA
ABCD is a parallelogram.
(v) Draw the angle bisector of ∠ABC intersecting CD at P.
P is the required point which is equidistant from AB and BC.

Question 9.
By using ruler and compass only, construct a quadrilateral ABCD in which AB = 6.5 cm, AD = 4cm and ∠DAB = 75°. C is equidistant from the sides AB and AD, also C is equidistant from the points A and B.
Solution:
Steps of Construction :

(i) Draw a line segment AB = 6.5 cm.
(ii) At A, draw a ray making an angle of 75° and cut off AD = 4 cm.
(iii) Draw the bisector of ∠DAB.
(iv) Draw perpendicular bisector of AB intersecting the angle bisector at C.
(v) Join CB and CD.
ABCD is the required quadrilateral.

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3

More Exercise

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Chapter Test

Question 1.
Find the surface area of a sphere of radius :
(i) 14 cm
(ii) 10.5 cm
Solution:
(i) Radius (r) = 14 cm
Surface area = \(4\pi { r }^{ 2 }=4\times \frac { 22 }{ 7 } \times 14\times 14 \) cm²
= 2964 cm²

Question 2.
Find the volume of a sphere of radius :
(i) 0.63 m
(ii) 11.2 cm
Solution:
(i) Radius (r) = 0.63 m
Volume = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }\)

Question 3.
Find the surface area of a sphere of diameter: (i) 21 cm (ii) 3.5 cm
Solution:
(i) Diameter = 21 cm
Radius (r) = \(\\ \frac { 21 }{ 2 } \) cm

Question 4.
A shot-put is a metallic sphere of radius 4.9 cm. If the density of the metal is 7.8 g per cm³, find the mass of the shot-put.
Solution:
Radius of the metallic shot-put = 4.9 cm
Volume = \(\frac { 4 }{ 3 } \pi { r }^{ 3 }\)

Question 5.
Find the diameter of a sphere whose surface area is 154 cm².
Solution:
Surface area of a sphere = 154 cm²

Question 6.
Find:
(i) the curved surface area.
(ii) the total surface area of a hemisphere of radius 21 cm.
Solution:
Radius of a hemisphere = 21 cm
(i) Curved surface area = 2πr²

Question 7.
A hemispherical brass bowl has inner- diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of Rs 16 per 100 cm².
Solution:
The inner diameter of hemispherical bowl = 10.5 cm

Question 8.
The radius of a spherical balloon increases from 7 cm to 14 cm as air is jumped into it. Find the ratio of the surface areas of the balloon in two cases.
Solution:
Original radius of balloon = 7 cm
Radius after filling the air in it = 14 cm
The surface area of balloon, the original position

Question 9.
A sphere and a cube have the same surface. Show that the ratio of the volume of the sphere to that of the cube is √6 : √π
Solution:
Let the edge of a cube = a
Surface area = 6a²
and surface area of sphere = 6a²

Question 10.
(a) If the ratio of the radii of two sphere is 3 : 7, find :
(i) the ratio of their volumes.
(ii) the ratio of their surface areas.
(b) If the ratio of the volumes of the two sphere is 125 : 64, find the ratio of their surface areas.
Solution:
(a) Ratio in radii of two spheres = 3 : 7
Let radius of the first sphere = 3x
and radius of the second sphere = 7x

Question 11.
A cube of side 4 cm contains a sphere touching its sides. Find the volume of the gap in between.
Solution:
Side of a cube = 4 cm
Volume (side)³ = 4 × 4 × 4 = 64 cm³
Diameter of sphere contained by this cube is d = 4 cm

Question 12.
Find the volume of a sphere whose surface area is 154 cm².
Solution:
Given that
Surface area of a sphere = 154 cm²

Question 13.
If the volume of a sphere is \(179 \frac { 2 }{ 3 } \) cm³, find its radius and the surface area.
Solution:
Given that
Volume of a sphere = \(179 \frac { 2 }{ 3 } \) cm³
= \(\\ \frac { 539 }{ 3 } \) cm³

Question 14.
A hemispherical bowl has a radius of 3.5 cm. What would be the volume of water it would contain?
Solution:
Radius of a hemispherical bowl (r) = 3.5 cm
= \(\\ \frac { 7 }{ 2 } \) cm

Question 15.
The water for a factory is stored in a hemispherical tank whose internal diameter is 14 m. The tank contains 50 kilolitres of water. Water is pumped into the tank to fill to its capacity. Find the volume of water pumped into the tank.
Solution:
Internal diameter of a hemispherical tank (r) = 14 m
Radius of the tank = \(\\ \frac { 14 }{ 2 } \) = 7 m
Water stored in it = 50 kilolitres of water

Question 16.
The surface area of a solid sphere is 1256 cm². It is cut into two hemispheres. Find the total surface area and the volume of a hemisphere. Take π = 3.14.
Solution:
Surface area of a solid sphere = 1256 cm²
By cutting it into two hemisphere,
Curved surface area of each hemisphere

Question 17.
Write whether the following statements are true or false. Justify your answer :
(i) The volume of a sphere is equal to two-third of the volume of a cylinder whose height and diameter are equal to the diameter of the sphere.
(ii) The volume of the largest right circular cone that can be fitted in a cube whose edge is 2r equals the volume of a hemisphere of radius r.
(iii) A cone, a hemisphere and a cylinder stand on equal bases and have the same height. The ratio of their volumes is 1 : 2 : 3.
Solution:
(i) The volume of a sphere is equal to the two third of the volume of a cylinder
whose height and diameter are equal to the diameter of the sphere.

(ii) The volume of the longest right circular cone that can be filled in a cube
whose edge is 2r equal to the volume of a hemisphere of radius r

(iii) A cone, a hemisphere and a cylinder stand on equal bases and have the same height.
The ratio of their volumes is 1 : 2 : 3

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Ex 14

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Ex 14

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Ex 14
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Chapter Test

Question 1.
A point moves such that its distance from a fixed line AB is always the same. What is the relation between AB and the path traveled by P ?
Solution:
Let point P moves in such a way that
it is at a fixed distance from the fixed line AB.

∴ It is a set of two lines l and m parallel to AB
drawn on either side of it at equal distance from it.

Question 2.
A point P moves so that its perpendicular distance from two given lines AB and CD are equal. State the locus of the point P.
Solution:
(i) When two lines AB and CD are parallel,
then the locus of the point P which is equidistant
from AB and CD is a line (l)
in the midway of AB and CD and parallel to them

(ii) If AB and CD are intersecting lines,
then the locus of the point P will be a
pair of the straight lines l and m which bisect
the angles between the given lines AB and CD.

Question 3.
P is a fixed point and a point Q moves such that the distance PQ is constant, what is the locus of the path traced out by the point Q ?
Solution:
∴ P is a fixed point and Q is a moving point
such that it is always at an equidistant from P.

∴ P is the centre of the path of Q which is a circle.
The distance between P and Q is the radius of the circle.
Hence locus of point Q is a circle with P as centre.

Question 4.
(i) AB is a fixed line. State the locus of the point P so that ∠APB = 90°.
(ii) A, B are fixed points. State the locus of the point P so that ∠APB = 60°.
Solution:
(i) AB is a fixed line and P is a point
such that ∠APB = 90°.

The locus of P will be the circle whose diameter is AB.
We know that the angle in a semi-circle is always equal to 90°.
∠APB = 90°
(ii) AB is a fixed line and P is a point such that ∠APB = 60°.
The locus of P will be a major segment of a circle whose AB is a chord.

Question 5.
Draw and describe the locus in each of the following cases :
(i) The locus of points at a distance 2.5 cm from a fixed line.
(ii) The locus of vertices of all isosceles triangles having a common base.
(iii) The locus of points inside a circle and equidistant from two fixed points on the circle.
(iv) The locus of centres of all circles passing through two fixed points.
(v) The locus of a point in rhombus ABCD which is equidistant from AB and AD. (1998)
(vi) The locus of a point in the rhombus ABCD which is equidistant from points A and C.
Solution:
1. Draw a given line AB.
2. Draw lines of l and m parallel to AB at a distance of 2.5 cm.
Lines l and m are the locus of point P which is at a distance of 2.5 cm.

(ii) ∆ABC is an isosceles triangle in which AB = AC.
From A, draw AD perpendicular to BC.
AD is the locus of the point A the vertices of ∆ABC.
In rt. ∆ABD and ∆ACD
Side AD = AD (Common)
Hyp. AB = AC (given)
∴ ∆ABD = ∆ACD (R.H.S. Axiom)
∴ BD = DC (c.p.c.t.)
Hence locus of vertices of isosceles triangles
having common base is the perpendicular bisector of BC.
(iii) (i) Draw a circle with centre O.

(ii) Take points A and B on it and join them.
(iii) Draw a perpendicular bisector of AB
which passes from O and meets the circle at C.
CE the diameter, which is the locus of a point inside the circle
and equidistant from two points A and B at the circle.
(iv) Let C1, C2, C3 be the centres of the circle
which pass through the two fixed points A and B.

Draw a line XY passing through these centres C1, C2, C3.
Hence locus of centres of circles passing through two points A and B
is the perpendicular bisector of the line segment joining the two fixed points.
(v) In rhombus ABCD, Join AC.

AC is the diagonal of rhombus ABCD
∴ AC bisect ∠A.
∴ Any point on AC, is the locus which is equidistant from AB and AD.
(vi) ABCD is a rhombus. Join BD

BD is the locus of a point in the rhombus which is equidistant from A and C.
Diagonal BD bisects  ∠B and ∠D.
Any point on BD will be equidistant from A and C.

Question 6.
Describe completely the locus of points in each of the following cases :
(i) mid-point of radii of a circle.
(ii) centre of a ball, rolling along a straight line on a level floor.
(iii) point in a plane equidistant from a given line.
(iv) point in a plane, at a constant distance of 5 cm from a fixed point (in the plane).
(v) centre of a circle of varying radius and touching two arms of ∠ADC.
(vi) centre of a circle of varying radius and touching a fixed circle, centre O, at a fixed point A on it.
(vii) centre of a circle of radius 2 cm and touching a fixed circle of radius 3 cm with centre 0.
Solution:
(i) The locus of midpoints of the radii of a circle
is another concentric circle with radius is
half of the radius of the given circle.

(ii) AB is the straight line on the ground and the ball is rolling on it
∴ locus of the centre of the ball is a line parallel A lo the given line AB.

(iii) AB is the given line and P is a point in the plane.

From P, draw a line CD and another line EF from P’ parallel to AB.
Thus CD and EF are the lines which are the locus of the point equidistant from AB
(iv) Take a point O and another point P such that OP = 5 cm.
with centre O and radius equal to OP, draw a circle.
Thus this circle is the locus of point P
which is at a distance of 5 cm from O, the given point.

(v) Draw the bisector BX of ∠ABC.
This bisector of an angle is the locus of the centre of a circle with different radii.
Any point on BX, is equidistant from the arms BA and BC of the ∠ABC.

(vi) A circle with centre O is given and one point A on it.
The locus of the centre of a circle which touches the circle
at the fixed point A on it, is a line joining the points O and A.

(vii) (a) If the circle with 2 cm as radius touches the given circle
externally then the locus of the centre of the circle
will be a concentric circle with radius 3+2 = 5 cm.

If the circle with 2 cm as radius touches the given circle with 3 cm as radius internally,
then the locus of the centre of the circle will be a concentric circle with radius 3-2 = 1 cm.

Question 7.
Using ruler and compasses construct :
(i) a triangle ABC in which AB = 5.5 cm, BC = 3.4 cm and CA = 4.9 cm.
(ii) the locus of points equidistant from A and C.
Solution:
(i) Draw BC = 3.4 and mark the arcs of 5.5 add 4.9 cm from B and C.
Join A, B and C.
ABC is the required triangle.
(ii) Draw ⊥ bisector of AC.
(iii) Draw an angle of 90° at AB at A which intersects ⊥ bisector at O.
Draw circle taking 0 as centre and OA as the radius.

Question 8.
Construct triangle ABC, with AB = 7 cm, BC = 8 cm and ∠ABC = 60°. Locate by construction the point P such that :
(i) P is equidistant from B and C and
(ii) P is equidistant from AB and BC
(iii) Measure and record the length of PB. (2000)
Solution:

(i) Take BC = 8 cm a long line segment. At B,
draw a ray BX making an angle of 60° with BC.
Cut off BA = 7 cm. and join AC.
(i) Draw the perpendicular bisector of BC.
(ii) Draw the angle bisector of ∠B which intersect
the perpendicular bisector of BC at P. P is the required point.
(iii) On measuring the length of BP = 4.6 cm (approx.)

Question 9.
A straight line AB is 8 cm long. Locate by construction the locus of a point which is :
(i) Equidistant from A and B.
(ii) Always 4 cm from the line AB.
(iii) Mark two points X and Y, which are 4 cm from AB and equidistant from A and B. Name the figure AXBY.(2008)
Solution:
Steps of construction:

(i) Draw a line segment AB = 8 cm.
(ii) With the help of compasses and ruler,
draw the perpendicular bisector l of AB which intersects AB at O.
(iii) Then any point on l, is equidistant from A and B.
(iv) Cut off OX = OY = 4 cm. The X and Y are the required loci,
which is equidistant from AB and also from A and B.
(v) Join AX, XB, BY and YA.
The figures so formed AXBY is the shape of a square because
its diagonals are equal and bisect each other at right angles.

Question 10.
Use ruler and compasses only for this question.
(i) Construct ∆ABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure arid record the length of PB. (2010)
Solution:
In ∆ABC, AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°

Steps of construction :
(a) (i) Draw a line segment BC = 6 cm
(ii) At, B draw a ray BX making an angle of 60° and cut off BA = 3.5 cm.
(iii) Join AC.
The ∆ABC is the required triangle.
(b) Draw the bisector BY of ∠ABC.
(c) Draw the perpendicular bisector of BC which intersects BY at P.
P is the required point P which is equidistant from BC and BA
and also equidistant from B and C.
On measuring PB it is 3.4 cm (approx)

Question 11.
Construct a triangle ABC with AB = 5.5 cm, AC = 6 cm and ∠BAC = 105°. Hence:
(i) Construct the locus of points equidistant from BA and BC.
(ii) Construct the locus of points equidistant from B and C.
(iii) Mark the point which satisfies the above two loci as P. Measure and write the length of PC.
Solution:
Steps of construction :

Construct the triangle ABC with AB = 5.5 cm
∠BAC = 105° and AC = 6 cm
(i) Points which are equidistant from BA and BC lies on the bisector of ∠ABC.
(ii) Points equidistant from B and C lies on the perpendicular bisector of BC.
Draw perpendicular bisector of BC.
The required point P is the point of intersection of the bisector of
∠ABC and the perpendicular bisector of BC.
(iii) Required length of PC = 4.8 cm.

Question 12.
In the given diagram, A, B and C are fixed collinear points; D is a fixed point outside the line: Locate

(i) the point P on AB such that CP = DP.
(ii) the points Q such that CQ = DQ = 3 cm. How many such points are possible?
(iii) the points R on AB such that DR = 4 cm. How many such points are possible?
(iv) the points S such that CS = DS and S is 4 cm away from the line CD. How many such points are possible?
(v) Are the points P, Q, R collinear?
(vi) Are the points P, Q, S collinear?
Solution:
Points A, B and C are collinear and D is any point outside AB.

(i) Join CD.
(ii) Draw the perpendicular bisector of CD which meets AB in P.
(iii) P is the required point such that CP = DP
(iv) With centres C and D, draw two arcs with 3 cm radius
which intersect each other at Q and Q’.
Hence there are two points Q and Q’ which are equidistant from C and D.
(v) With centre D, and radius 4 cm draw an arc which intersects AB at R and R’
∴ R and R’ are the two point on AB.
(vi) With centre C and D, draw arcs with a radius equal to
4 cm which intersects each other in S and S’.
∴ There can be two such points which are equidistant from C and D.
(vii) No P, Q, R are not collinear.
(viii) Yes, P, Q, S are collinear.

Question 13.
Points A, B and C represent position of three towers such that AB = 60 m, BC = 73m and CA = 52 m. Taking a scale of 10 m to 1 cm, make an accurate drawing of ∆ABC. Find by drawing, the location of a point which is equidistant from A, B and C, and its actual distance from any of the towers.
Solution:
AB = 60 mm = 6.0 cm, BC = 73 mm = 7.3 cm
and CA = 52 mm = 5.2 cm.

(i) Draw a line segment BC = 7.3cm
(ii) With Centre B and radius 6cm and with centre C
and radius 5.2 cm, draw two arcs intersecting each other at A
(iii) Joining AB and AC.
(iv) Draw the perpendicular bisector of AB, BC and CA respectively,
which intersect each other at point P. Join PB.
P is equidistant from A, B and C on measuring PB = 3.7 cm.
Actual distance = 37 m.

Question 14.
Draw two intersecting lines to include an angle of 30°. Use ruler and compasses to locate points which are equidistant from these lines and also 2 cm away from their point of intersection. How many such points exist ? (1990)
Solution:
(i) Two lines AB and CD intersect each other at O.

(ii) Draw the bisector of ∠BOD and ∠AOD
(iii) With centre O and radius equal to 2 cm.
marks points on the bisector of angles at P, Q, R and S respectively.
Hence there are four points which are equidistant
from AB and CD and 2 cm from 0, the point of intersection of AB and CD.

Question 15.
Without using set square or protractor, construct the quadrilateral ABCD in which ∠BAD = 45°, AD = AB = 6 cm, BC = 3.6 cm and CD = 5 cm.
(i) Measure ∠BCD.
(ii) Locate the point P on BD which is equidistant from BC and CD. (1992)
Solution:
(i) Take AB = 6 cm long
(ii) AT A, draw the angle of 45° and cut off AD = 6 cm

(iii) With centre D and radius 5 cm and with centre B,
and radius 3.5 cm draw two arcs intersecting each other at C.
(iv) Join CD and CB and join BD
ABCD is the required quadrilateral.
(v) On measuring ∠BCD = 65°.
(vi) Draw the bisector of ∠BCD which intersects BD at P.
P is the required point which is equidistant from CD and CB.

Question 16.
Without using set square or protractor, construct rhombus ABCD with sides of length 4 cm and diagonal AC of length 5 cm. Measure ∠ABC. Find the point R on AD such that RB = RC. Measure the length of AR. (1990)

Solution:
(i) Take AB = 4 cm
(ii) With centre A, draw an arc of 5 cm radius
and with B draw another arc of radius 4 cm intersecting each other at C.
(iii) Join AC and BD.
(iv) Again with centre A and C,
draw two arcs of radius 4 cm intersecting each other on D.
(v) Join AD and CD.
ABCD is the required rhombus and on measuring the ∠ABC, it is 78°.
(vi) Draw perpendicular bisector of BC intersecting AD at R.
On measuring the length of AR, it is equal to 1.2 cm.

Question 17.
Without using set-squares or protractor construct :
(i) Triangle ABC, in which AB = 5.5 cm, BC = 3.2 cm and CA = 4.8 cm.
(ii) Draw the locus of a point which moves so that it is always 2.5 cm from B.
(iii) Draw the locus of a point which moves so that it is equidistant from the sides BC and CA.
(iv) Mark the point of intersection of the loci with the letter P and measure PC. (1994)
Solution:
Steps of Construction :
(i) Draw BC = 3.2 cm long.
(ii) With centre B and radius 5.5 cm
and with centre C and radius 4.8 cm
draw arcs intersecting each other at A.

(iiii) Join AB and AC.
(iv) Draw the bisector of ∠BCA.
(v) With centre B and radius 2.5 cm,
draw an arc intersecting the angle bisector of ∠BCA at P and P’.
P and P’ are two loci which satisfy the given condition.
On measuring CP and CP’
CP = 3.6 cm and CP’ =1.1 cm.

Question 18.
By using ruler and compasses only, construct an isosceles triangle ABC in which BC = 5 cm, AB = AC and ∠BAC = 90°. Locate the point P such that :
(i) P is equidistant from the sides BC and AC.
(ii) P is equidistant from the points B and C.
Solution:
Steps of Construction :
(i) Take BC = 5.0 cm and bisect it at D.

(ii) Taking BC as diameter, draw a semicircle.
(iii) At D, draw a perpendicular intersecting the circle at A
(iv) Join AB and AC.
(v) Draw the angle bisector of C intersecting
the perpendicular at P. P is the required point.

Question 19.
Using ruler and compasses only, construct a quadrilateral ABCD in which AB = 6 cm, BC = 5 cm, ∠B = 60°, AD = 5 cm and D is equidistant from AB and BC. Measure CD. (1983)
Solution:
Steps of Construction :
(i) Draw AB = 6 cm

(ii) At B, draw angle of 60° and cut off BC = 5 cm.
(iii) Draw the angle bisector of ∠B.
(iv) With centre A and radius 5 cm. draw an arc
which intersects the angle bisector of ∠B at D
(v) Join AD and DC.
ABCD in the required quadrilateral.
On measuring CD, it is 5.3 cm (approx).

Question 20.
Construct an isosceles triangle ABC such that AB = 6 cm, BC = AC = 4 cm. Bisect ∠C internally and mark a point P on this bisector such that CP = 5 cm. Find the points Q and R which are 5 cm from P and also 5 cm from the line AB (2001)
Solution:
Steps of Construction :
(i) Draw a line AB = 6 cm

(ii) With centre A and B and radius 4 cm,
draw two arcs intersecting each other at C.
(iii) Join CA and CB
(iv) Draw the bisector of ∠C and cut off CP = 5 cm
(v) Draw a line XY parallel to AB at a distance of 5 cm.
(vi) From P, draw arcs of radius 5 cm each intersecting
the line XY at Q and R. Hence Q and R are the required points.

Question 21.
Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark two chords AB and AC of the circle of length 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC, (1995)
Solution:
Steps of Construction :
(i) With centre 0 and radius 4 cm draw a circle.
(ii) Take point A on this circle.

(iii) With centre A and radius 6 cm draw an arc cutting the circle at B.
(iv) Again with radius 5 cm, draw another arc cutting the circle at C.
(v) Join AB and AC.
(vi) Draw the perpendicular bisector of AC.
Any point on it, will be equidistant from A and C.
(vii) Draw the angle bisector of ∠A intersecting
the perpendicular bisector of AC at P. P is the required locus.

Question 22.
Ruler and compasses only may be used in this question. All construction lines and arcs must be clearly shown, and be of sufficient length and clarity to permit assessment.
(i) Construct a triangle ABC, in which BC = 6 cm, AB = 9 cm. and ∠ABC = 60°.
(ii) Construct the locus of all points, inside ∆ABC, which are equidistant from B and C.
(iii) Construct the locus of the vertices of the triangles with BC as base, which are equal in area to ∆ABC.
(iv) Mark the point Q, in your construction, which would make ∆QBC equal in area to ∆ABC, and isosceles.
(v) Measure and record the length of CQ. (1998)
Solution:
Steps of Construction :
(i) Draw AB = 9 cm
(ii) At B draw an angle of 60° and cut off BC = 6 cm.
(iii) Join AC

(iv) Draw perpendicular bisector of BC.
All points on it will be equidistant from B and C.
(v) From A, draw a line XY parallel to BC.
(vi) Produce the perpendicular bisector of BC to meet XY in Q.
(vii) Join QC and QB.
∆QBC will be the triangle equal in area to ∆ABC
because these are on the same base BC and between the same parallel lines.
On measuring, the length of CQ is 8.2 cm (approx.).

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 14 Locus Ex 14 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2

More Exercise

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Chapter Test

Take π = \(\\ \frac { 22 }{ 7 } \) unless stated otherwise.

Question 1.
Write whether the following statements are true or false. Justify your answer.
(i) If the radius of a right circular cone is halved and its height is doubled, the volume will remain unchanged.
(ii) A cylinder and a right circular cone are having the same base radius and same height. The volume of the cylinder is three times the volume of the cone.
(iii) In a right circular cone, height, radius and slant height are always the sides of a right triangle.
Solution:
(i) If the radius of a right circular cone is halved and its height is doubled,
then the volume will remain unchanged
It is wrong as

(ii) A cylinder and a right circular cone are having the same base radius
and same height the volume of the cylinder is three times the volume of cone – It is true as
Volume of cylinder = \(\pi { r }^{ 2 }h=3\times \frac { 1 }{ 3 } \pi { r }^{ 2 }h\) = 3(volume of cone)
(iii) In a right circular cone, height, radius and slant height are always the sides of a right triangle
It is true as in a cone and in a right-angled triangle.
Hypotenuse (slant x height) = r² + h²
and cone is formed by revolving the right triangle about the perpendicular.

Question 2.
Find the curved surface area of a right circular cone whose slant height is 10 cm and base radius is 7 cm.
Solution:
10 Slant height of a cone (l) = 10 cm
and radius of the base = 7 cm
Curved surface area = πrl
= \(\\ \frac { 22 }{ 7 } \) × 7 × 10 = 220 cm²

Question 3.
Diameter of the base of a cone is 10.5 cm and slant height is 10 cm. Find its curved surface area.
Solution:
The diameter of the base of a cone = 10.5cm
Its radius (r) = \(\\ \frac { 10.5 }{ 7 } \) = 5.25 cm
and slant height (l) = 10 cm
Curved surface area = πrl
= \(\\ \frac { 22 }{ 7 } \) × 5.25 × 10 cm²
= 165.0 cm²

Question 4.
Curved surface area of a cone is 308 cm² and its slant height is 14 cm. Find ,
(i)radius of the base
(ii)total surface area of the cone.
Solution:
Curved surface area of a cone = 308 cm²
Slant height = 14 cm

Question 5.
Find the volume of the right circular cone with
(i) radius 6 cm and height 7 cm
(ii) radius 3.5 cm and height 12 cm.
Solution:
(i) Radius of cone (r) = 6 cm
and height (h) = 7 cm
Volume = \(\frac { 1 }{ 3 } \pi { r }^{ 2 }h \)

Question 6.
Find the capacity in litres of a conical vessel with
(i) radius 7 cm, slant height 25 cm
(ii) height 12 cm, slant height 13 cm
Solution:
(i) Radius = 7 cm
and slant height (l) = 25 cm

Question 7.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kiloliters ?
Solution:
Diameter of top of conical pit = 3.5 m
Radius (r) = \(\\ \frac { 3.5 }{ 2 } \) = 1.75 m
and depth (h) = 12m

Question 8.
If the volume of a right circular cone of height 9 cm is 48π cm³, find the diameter of its base.
Solution:
Volume of a right circular cone = 48π cm³
Height (h) = 9 cm

Question 9.
The height of a cone is 15 cm. If its volume is 1570 cm³, find the radius of the base. (Use π = 3.14)
Solution:
Height of cone (h) = 15 cm
Volume = 1570 cm³

Question 10.
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white washing its curved surface area at the rate of Rs 210 per 100 m².
Solution:
Slant height of conical tomb (l) = 25 m
and base diameter = 14 m
Radius(r) = \(\\ \frac { 14 }{ 2 } \) = 7m

Question 11.
A conical tent is 10 m high and the radius of its base is 24 m. Find :
(i) slant height of the tent.
(ii) cost of the canvas required to make the tent, if the cost of 1 m² canvas is Rs 70.
Solution:
Height of a conical tent (h) = 10 m
and radius (r) = 24 m

Question 12.
A Jocker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the cloth required to make 10 such caps.
Solution:
Base radius of a conical cap = 7 cm
and height (h) = 24 cm

= 550 x 10
= 5500 cm²

Question 13.
(a) The ratio of the base radii of two right circular cones of the same height is 3 : 4. Find the ratio of their volumes.
(b) The ratio of the heights of two right circular cones is 5 : 2 and that of their base radii is 2 : 5. Find the ratio of their volumes.
(c) The height and the radius of the base of a right circular cone is half the corresponding height and radius of another bigger cone. Find:
(i) the ratio of their volumes.
(ii) the ratio of their lateral surface areas.
Solution:
(i) The ratio in base radii of two right circular cones of the same height = 3 : 4
Let h be the height and radius of first cone = 3x and
Radius of second cone = 4x

Question 14.
Find what length of canvas 2 m in width is required to make a conical tent 20 m in diameter and 42 m in slant height allowing 10% for folds and the stitching. Also find the cost of the canvas at the rate of Rs 80 per metre.
Solution:
Diameter of the base of the conical tent = 20 m
Radius (r) = \(\\ \frac { 20 }{ 2 } \) = 10 m
and slant height (h) = 42 m

Question 15.
The perimeter of the base of a cone is 44 cm and the slant height is 25 cm. Find the volume and the curved surface of the cone.
Solution:
Perimeter of the base of a cone = 44 cm

Question 16.
The volume of a right circular cone is 9856 cm³ and the area of its base is 616 cm². Find
(i) the slant height of the cone.
(ii) total surface area of the cone.
Solution:
Volume of a circular cone = 9856 cm³
Area of the base = 616 cm²

Question 17.
A right triangle with sides 6 cm, 8 cm and 10 cm is revolved about the side 8 cm. Find the volume and the curved surface of the cone so formed. (Take π = 3.14)
Solution:
Sides of a right triangle are 6 cm and 8 cm
It is revolved around 8 cm side
Radius (r) = 6 cm
Height (h) = 8 cm
Slant height (l) = 10 cm

Question 18.
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to its base. If its volume be \(\\ \frac { 1 }{ 27 } \) of the volume of the given cone, at what height above the base is the section cut?
Solution:
Height of a cone (H) = 30 cm
A small cone is cut off from the top of the cone given


h = 10 cm
∴ A line parallel to base at a distance of 30 – 10 = 20 cm is drawn.

Question 19.
A semi-circular lamina of radius 35 cm is folded so that the two bounding radii are joined together to form a cone. Find
(i) the radius of the cone.
(ii) the (lateral) surface area of the cone.
Solution:
Radius of a semi-circular lamina = 35 cm
By folding it a cone is formed whose slant height (l) = r = 35
and half circumference = circumference of the top of the cone

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.1

More Exercise

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Chapter Test

Take π = \(\\ \frac { 22 }{ 7 } \) unless stated otherwise.

Question 1.
Find the total surface area of a solid cylinder of radius 5 cm and height 10 cm. Leave your answer in terms of π.
Solution:
Radius of the cylinder (r) = 5 cm
Height (h) = 10 cm
Total surface area = 2πr (h + r)
= 2π x 5(10 + 5) cm²
= 10 x 15π
= 150π cm²

Question 2.
An electric geyser is cylindrical in shape, having a diameter of 35 cm and height 1.2m. Neglecting the thickness of its walls, calculate
(i) its outer lateral surface area,
(ii) its capacity in litres.
Solution:
Diameter of cylindrical geyser = 35 cm
Radius (r) = \(\\ \frac { 35 }{ 2 } \) cm
Height = 1.2 m = 120 cm

Question 3.
A school provides milk to the students daily in cylindrical glasses of diameter 7 cm. If the glass is filled with milk upto a height of 12 cm, find how many litres of milk is needed to serve 1600 students.
Solution:
Number of students = 1600
Diameter of cylindrical glasses = 7 cm
Radius (r) = \(\\ \frac { 7 }{ 2 } \) cm

Question 4.
In the given figure, a rectangular tin foil of size 22 cm by 16 cm is wrapped around to form a cylinder of height 16 cm. Find the volume of the cylinder.

Solution:
Length of rectangular tin foil (l) = 22 cm
and breadth (b) = 16 cm
By folding lengthwise, the radius of the cylinder

Question 5.
(i) How many cubic metres of soil must be dug out to make a well 20 metres deep and 2 metres in diameter?
(ii) If the inner curved surface of the well in part (i) above is to be plastered at the rate of Rs 50 per m², find the cost of plastering.
Solution:
(i) Depth of well (h) = 20 m
and diameter = 2 m

Question 6.
A roadroller (in the shape of a cylinder) has a diameter 0.7 m and its width is 1.2 m. Find the least number of revolutions that the roller must make in order to level a playground of size 120 m by 44 m.
Solution:
Diameter of a road roller = 0.7 m
Radius (r) = \(\\ \frac { 0.7 }{ 2 } \) = 0.35 m
and width (h) = 1.2 m

Question 7.
If the volume of a cylinder of height 7 cm is 448 π cm³, find its lateral surface area and total surface area.
Solution:
Volume of a cylinder = 448 π cm³
Height (h) = 7 cm

Question 8.
A wooden pole is 7 m high and 20 cm in diameter. Find its weight if the wood weighs 225 kg per m³.
Solution:
Height of a wooden pole (h) = 7 m
Diameter = 20 cm

Question 9.
The area of the curved surface of a cylinder is 4400 cm², and the circumference of its base is 110 cm. Find
(i) the height of the cylinder.
(ii) the volume of the cylinder.
Solution:
Area of the curved surface of a cylinder = 4400 cm²
Circumference of base = 110 cm

Question 10.
A cylinder has a diameter of 20 cm. The area of curved surface is 1000 cm². Find
(i) the height of the cylinder correct to one decimal place.
(ii) the volume of the cylinder correct to one decimal place. (Take π = 3.14)
Solution:
Diameter of a cylinder = 20 cm
Radius (r) = \(\\ \frac { 20 }{ 2 } \) = 10 cm
Curved surface area = 1000 cm²

Question 11.
The barrel of a fountain pen, cylindrical in shape, is 7 cm long and 5 mm in diameter. A full barrel of ink in the pen will be used up when writing 310 words on an average. How many words would use up a bottle of ink containing one-fifth of a litre?
Answer correct to the nearest. 100 words.
Solution:
Height of cylindrical barrel of a pen (h) = 7 cm
Diameter = 5 mm

Question 12.
Find the ratio between the total surface area of a cylinder to its curved surface area given that its height and radius are 7.5 cm and 3.5 cm.
Solution:
Radius of a cylinder (r) = 3.5 cm
and height (h) = 7.5 cm
Total surface area = 2πr(r + h)

Question 13.
The radius of the base of a right circular cylinder is halved and the height is doubled. What is the ratio of the volume of the new cylinder to that of the original cylinder?
Solution:
Let the radius of the base of a right circular cylinder = r
and height (h) = h
Volume = πr²h

Question 14.
(i) The sum of the radius and the height of a cylinder is 37 cm and the total surface area of the cylinder is 1628 cm². Find the height and the volume of the cylinder.
(ii) The total surface area of a cylinder is 352 cm². If its height is 10 cm, then find the diameter of the base.
Solution:
Sum of radius and height of a cylinder = 37 cm
Total surface area = 1628 cm²
Let r be radius and h be height, then r × h = 37
and 2πr(r + h) = 1628

Question 15.
The ratio between the curved surface and the total surface of a cylinder is 1 : 2. Find the volume of the cylinder, given that its total surface area is 616 cm².
Solution:
Ratio between curved surface area and total surface area = 1 : 2
Total surface area = 616 cm²

Question 16.
Two cylindrical jars contain the same amount of milk. If their diameters are in the ratio 3 : 4, find the ratio of their heights.
Solution:
Volume of two cylinders is the same
Diameter of both cylinder are in the ratio = 3 : 4

Question 17.
A rectangular sheet of tin foil of size 30 cm x 18 cm can be rolled to form a cylinder in two ways along length and along breadth. Find the ratio of volumes of the two cylinders thus formed.
Solution:
Size of the sheet = 30 cm × 18 cm
(i) By rolling lengthwise,
The circumference of the cylinder = 2πr = 30

Question 18.
A cylindrical tube open at both ends is made of metal. The internal diameter of the tube is 11.2 cm and its length is 21 cm. The metal thickness is 0.4 cm. Calculate the volume of the metal.
Solution:
Internal diameter of a metal tube = 11.2 cm
and radius (r) = \(\\ \frac { 11.2 }{ 2 } \) = 5.6 cm
Length (h) = 21 cm
Thickness of metal = 0.4 cm
External radius (R) = 5.6 + 0.4 = 6.0 cm

Question 19.
The given figure shows a metal pipe 77 cm long. The inner diameter of a cross-section is 4 cm and the outer one is 4.4 cm. Find its
(i) inner curved surface area
(ii) outer curved surface area
(iii) total surface area.

Solution:
In the given figure,
Length of metal pipe (h) = 77 cm
Inner diameter = 4 cm

Question 20.
A lead pencil consists of a cylinder of wood with a solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
Solution:
Diameter of the pencil = 7 mm
Radius (R) = \(\\ \frac { 7 }{ 2 } \) mm = \(\\ \frac { 7 }{ 20 } \) cm
Diameter of graphite (lead) = 1 mm

Question 21.
A soft drink is available in two packs
(i) a tin can with a rectangular base of length 5 cm and width 4 cm, having a height of 15 cm and
(ii) a plastic cylinder with circular base of diameter 7 cm and height 10 cm. Which container has greater capacity and by how much?
Solution:
(i) Base of the tin of rectangular base = 5 cm × 4 cm
Height = 15 cm
Volume = lbh = 5 × 4 × 15 = 300 cm³
(ii) Base diameter of cylindrical plastic cylinder = 7 cm

Question 22.
A cylindrical roller made of iron is 2 m long. Its inner diameter is 35 cm and the thickness is 7 cm all round. Find the weight of the roller in kg, if 1 cm³ of iron weighs 8 g.
Solution:
Length of cylindrical roller (h) = 2 m = 200 cm
Diameter = 35 cm
Inner radius = \(\\ \frac { 35 }{ 2 } \) cm
Thickness = 7 cm

We hope the ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.1 help you. If you have any query regarding ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 17 Mensuration Ex 17.1, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Chapter Test

Question 1.
Find the length of the tangent drawn to a circle of radius 3 cm, from a point distant 5 cm from the centre.
Solution:
In a circle with centre O and radius 3 cm
and P is at a distance of 5 cm.

Question 2.
A point P is at a distance 13 cm from the centre C of a circle and PT is a tangent to the given circle. If PT = 12 cm, find the radius of the circle.
Solution:
CT is the radius
CP = 13 cm and tangent PT = 12 cm

Question 3.
The tangent to a circle of radius 6 cm from an external point P, is of length 8 cm. Calculate the distance of P from the nearest point of the circle.

Solution:
Radius of the circle = 6 cm
and length of tangent = 8 cm
Let OP be the distance
i.e. OA = 6 cm, AP = 8 cm .
OA is the radius

Question 4.
Two concentric circles are of the radii 13 cm and 5 cm. Find the length of the chord of the outer circle which touches the inner circle.
Solution:
Two concentric circles with centre O
OP and OB are the radii of the circles respectively, then
OP = 5 cm, OB = 13 cm.

Question 5.
Two circles of radii 5 cm and 2-8 cm touch each other. Find the distance between their centres if they touch :
(i) externally
(ii) internally.
Solution:
Radii of the circles are 5 cm and 2.8 cm.
i.e. OP = 5 cm and CP = 2.8 cm.

(i) When the circles touch externally,
then the distance between their centres = OC = 5 + 2.8 = 7.8 cm.
(ii) When the circles touch internally,
then the distance between their centres = OC = 5.0 – 2.8 = 2.2 cm

Question 6.
(a) In figure (i) given below, triangle ABC is circumscribed, find x.
(b) In figure (ii) given below, quadrilateral ABCD is circumscribed, find x.

Solution:
(a) From A, AP and AQ are the tangents to the circle
∴ AQ = AP = 4cm

Question 7.
(a) In figure (i) given below, quadrilateral ABCD is circumscribed; find the perimeter of quadrilateral ABCD.
(b) In figure (ii) given below, quadrilateral ABCD is circumscribed and AD ⊥ DC ; find x if radius of incircle is 10 cm.

Solution:
(a) From A, AP and AS are the tangents to the circle
∴AS = AP = 6
From B, BP and BQ are the tangents
∴BQ = BP = 5
From C, CQ and CR are the tangents

Question 8.
(a) In the figure (i) given below, O is the centre of the circle and AB is a tangent at B. If AB = 15 cm and AC = 7.5 cm, find the radius of the circle.
(b) In the figure (ii) given below, from an external point P, tangents PA and PB are drawn to a circle. CE is a tangent to the circle at D. If AP = 15 cm, find the perimeter of the triangle PEC.

Solution:
(i) Join OB
∠OBA = 90°
(Radius through the point of contact is
perpendicular to the tangent)

Question 9.
(a) If a, b, c are the sides of a right triangle where c is the hypotenuse, prove that the radius r of the circle which touches the sides of the triangle is given by
\(r= \frac { a+b-c }{ 2 } \)
(b) In the given figure, PB is a tangent to a circle with centre O at B. AB is a chord of length 24 cm at a distance of 5 cm from the centre. If the length of the tangent is 20 cm, find the length of OP.

Solution:
(a) Let the circle touch the sides BC, CA and AB
of the right triangle ABC at points D, E and F respectively,
where BC = a, CA = b
and AB = c (as showing in the given figure).

Question 10.
Three circles of radii 2 cm, 3 cm and 4 cm touch each other externally. Find the perimeter of the triangle obtained on joining the centres of these circles.
Solution:
Three circles with centres A, B and C touch each other externally
at P, Q and R respectively and the radii of these circles are
2 cm, 3 cm and 4 cm.

Question 11.
(a) In the figure (i) given below, the sides of the quadrilateral touch the circle. Prove that AB + CD = BC + DA.
(b) In the figure (ii) given below, ABC is triangle with AB = 10cm, BC = 8cm and AC = 6cm (not drawn to scale). Three circles are drawn touching each other with vertices A, B and C as their centres. Find the radii of the three circles

Solution:
(a) Given: Sides of quadrilateral ABCD touch the circle at
P, Q, R and S respectively.

Question 12.
(a) ln the figure (i) PQ = 24 cm, QR = 7 cm and ∠PQR = 90°. Find the radius of the inscribed circle ∆PQR

(b) In the figure (ii) given below, two concentric circles with centre O are of radii 5 cm and 3 cm. From an external point P, tangents PA and PB are drawn to these circles. If AP = 12cm, find BP.

Solution:
(a) In the figure, a circle is inscribed in the triangle PQR
which touches the sides. O is centre of the circle.
PQ = 24cm, QR = 7 cm ∠PQR = 90°
OM is joined.

Question 13.
(a) In the figure (i) given below, AB = 8 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all three semi-circles as shown, find its radius.

(b) In the figure (ii) given below, equal circles with centres O and O’ touch each other at X. OO’ is produced to meet a circle O’ at A. AC is tangent to the circle whose centre is O. O’D is perpendicular to AC. Find the value of :
(i) \(\\ \frac { AO’ }{ AO } \)
(ii) \(\frac { area\quad of\quad \Delta ADO’ }{ area\quad of\quad \Delta ACO } \)

Solution:
(a) Let x be the radius of the circle
with centre C and radii of each equal

Question 14.
The length of the direct common tangent to two circles of radii 12 cm and 4 cm is 15 cm. Calculate the distance between their centres.
Solution:
Let R and r be the radii of the circles
with centre A and B respectively
Let TT’ be their common tangent.

Hence distance between their centres = 17 cm Ans.

Question 15.
Calculate the length of a direct common tangent to two circles of radii 3 cm and 8 cm with their centres 13 cm apart.
Solution:
Let A and B be the centres of the circles
whose radii are 8 cm and 3 cm and
let TT’ length of their common tangent and AB = 13 cm.

Question 16.
In the given figure, AC is a transverse common tangent to two circles with centres P and Q and of radii 6 cm and 3 cm respectively. Given that AB = 8 cm, calculate PQ.

Solution:
AC is a transverse common tangent to the two circles
with centre P and Q and of radii 6 cm and 3 cm respectively
AB = 8 cm. Join AP and CQ.

Question 17.
Two circles with centres A, B are of radii 6 cm and 3 cm respectively. If AB = 15 cm, find the length of a transverse common tangent to these circles.
Solution:
AB = 15 cm.
Radius of the circle with centre A = 6 cm
and radius of second circle with radius B = 3 cm.

Question 18.
(a) In the figure (i) given below, PA and PB are tangents at a points A and B respectively of a circle with centre O. Q and R are points on the circle. If ∠APB = 70°, find (i) ∠AOB (ii) ∠AQB (iii) ∠ARB
(b) In the figure (ii) given below, two circles touch internally at P from an external point Q on the common tangent at P, two tangents QA and QB are drawn to the two circles. Prove that QA = QB.

Solution:
(a) To find : (i) ∠AOB, (ii) ∠AQB, (iii) ∠ARB
Given: PA and PB are tangents at the points A and B respectively
of a circle with centre O and OA and OB are radii on it.
∠APB = 70°
Construction: Join AB

Question 19.
In the given figure, AD is a diameter of a circle with centre O and AB is tangent at A. C is a point on the circle such that DC produced intersects the tangent of B. If ∠ABC = 50°, find ∠AOC.

Solution:
Given AB is tangent to the circle at A and OA is radius, OA ⊥ AB
In ∆ABD

Question 20.
In the given figure, tangents PQ and PR are drawn from an external point P to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, Find ∠RQS

Solution:
In the given figure,
PQ and PR are tangents to the circle with centre O drawn from P
∠RPQ = 30°
Chord RS || PQ is drawn
To find ∠RQS
∴ PQ = PR (tangents to the circle)

Question 21.
(a) In the figure (i) given below, PQ is a tangent to the circle at A, DB is a diameter, ∠ADB = 30° and ∠CBD = 60°, calculate (i) ∠QAB (ii) ∠PAD (iii) ∠CDB.

(b) In the figure (ii) given below, ABCD is a cyclic quadrilateral. The tangent to the circle at B meets DC produced at F. If ∠EAB = 85° and ∠BFC = 50°, find ∠CAB.

Solution:
(a) PQ is tangent and AD is chord
(i) ∴ ∠QAB = ∠BDA = 30°
(Angles in the alternate segment)
(ii) In ∆ADB,
∠DAB = 90° (Angle in a semi-circle)



⇒ ∠CAB = 35°

Question 22.
(a) In the figure (i) given below, O is the centre of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and z. (2015)
(b) In the figure (ii) given below, O is the centre of the circle. PS and PT are tangents and ∠SPT = 84°. Calculate the sizes of the angles TOS and TQS.

Solution:
Consider the following figure:
TS ⊥ SP,
∠TSR = ∠OSP = 90°
In ∆TSR,
∠TSR + ∠TRS + ∠RTS = 180°

Question 23.
In the given figure, O is the centre of the circle. Tangents to the circle at A and B meet at C. If ∠ACO = 30°, find
(i) ∠BCO (ii) ∠AOR (iii) ∠APB

Solution:
(i) ∠BCO = ∠ACO = 30°
(∵ C is the intersecting point of tangent AC and BC)
(ii) ∠OAC = ∠OBC = 90°
∵∠AOC = ∠BOC = 180° – (90° + 30°) = 60°
(∵ sum of the three angles a ∆ is 180°)

Question 24.
(a) In the figure (i) given below, O is the centre of the circle. The tangent at B and D meet at P. If AB is parallel to CD and ∠ ABC = 55°. find: (i)∠BOD (ii) ∠BPD
(b) In the figure (ii) given below. O is the centre of the circle. AB is a diameter, TPT’ is a tangent to the circle at P. If ∠BPT’ = 30°, calculate : (i)∠APT (ii) ∠B OP.

Solution:
(a) AB || CD
(i) ∠ABC = ∠BCD (Alternate angles)
⇒ ∠BCD = 55°

Question 25.
In the adjoining figure, ABCD is a cyclic quadrilateral.

The line PQ is the tangent to the circle at A. If ∠CAQ : ∠CAP = 1 : 2, AB bisects ∠CAQ and AD bisects ∠CAP, then find the measure of the angles of the cyclic quadrilateral. Also prove that BD is a diameter of the circle.
Solution:
ABCD is a cyclic quadrilateral.
PAQ is the tangent to the circle at A.
∠CAD : ∠CAP = 1 : 2.
AB and AD are the bisectors of ∠CAQ and ∠CAP respectively

Question 26.
In a triangle ABC, the incircle (centre O) touches BC, CA and AB at P, Q and R respectively. Calculate (i) ∠QOR (ii) ∠QPR given that ∠A = 60°.
Solution:
OQ and OR are the radii and AC and AB are tangents.
OQ ⊥ AC and OR ⊥ AB
Now in the quad. AROQ

Question 27.
(a) In the figure (0 given below, AB is a diameter. The tangent at C meets AB produced at Q, ∠CAB = 34°. Find
(i) ∠CBA (ii) ∠CQA (2006)

(b) In the figure (ii) given below, AP and BP are tangents to the circle with centre O. Given ∠APB = 60°, calculate.
(i) ∠AOB (ii) ∠OAB (iii) ∠ACB.

Solution:
(a) AB is the diameter.

Question 28.
(a) In the figure (i) given below, O is the centre of the circumcircle of triangle XYZ. Tangents at X and Y intersect at T. Given ∠XTY = 80° and ∠XOZ = 140°, calculate the value of ∠ZXY. (1994)
(b) In the figure (ii) given below, O is the centre of the circle and PT is the tangent to the circle at P. Given ∠QPT = 30°, calculate (i) ∠PRQ (ii) ∠POQ.

Solution:
(a) Join OY, OX and OY are the radii of the circle
and XT and YT are the tangents to the circle.

Question 29.
Two chords AB, CD of a circle intersect internally at a point P. If
(i) AP = cm, PB = 4 cm and PD = 3 cm, find PC.
(ii) AB = 12 cm, AP = 2 cm, PC = 5 cm, find PD.
(iii) AP = 5 cm, PB = 6 cm and CD = 13 cm, find CP.
Solution:
In a circle, two chords AB and CD intersect
each other at P internally.

Question 30.
(a) In the figure (i) given below, PT is a tangent to the circle. Find TP if AT = 16 cm and AB = 12 cm.

(b) In the figure given below, diameter AB and chord CD of a circle meet at P. PT is a tangent to the circle at T. CD = 7.8 cm, PD = 5 cm, PB = 4 cm. Find (i) AB. (ii)the length of tangent PT.

Solution:
(a) PT is the tangent to the circle and AT is a secant.
PT² = TA × TB
Now TA = 16 cm, AB = 12 cm
TB = AT – AB = 16 – 12 = 4 cm
∴ PT² = 16 + 4 = 64 = (8)²
⇒ PT = 8 cm or TP = 8 cm
(b) PT is tangent and PDC is secant out to the circle
∴ PT² = PC × PD

Question 31.
PAB is secant and PT is tangent to a circle
(i) PT = 8 cm and PA = 5 cm, find the length of AB.
(ii) PA = 4.5 cm and AB = 13.5 cm, find the length of PT.
Solution:
∵ PT is the tangent and PAB is the secant of the circle.

Question 32.
In the adjoining figure, CBA is a secant and CD is tangent to the circle. If AB = 7 cm and BC = 9 cm, then
(i) Prove that ∆ACD ~ ∆DCB.
(ii) Find the length of CD.

Solution:
In ∆ACD and ∆DCB
∠C = ∠C (common)
∠CAD = ∠CDB

Question 33.
(a) In the figure (i) given below, PAB is secant and PT is tangent to a circle. If PA : AB = 1:3 and PT = 6 cm, find the length of PB.
(b) In the figure (ii) given below, ABC is an isosceles triangle in which AB = AC and Q is mid-point of AC. If APB is a secant, and AC is tangent to the circle at Q, prove that AB = 4 AP.

Solution:
(a) In the figure (i),
PAB is secant and PT is the tangent to the circle.
PT² = PA × PB

Question 34.
Two chords AB, CD of a circle intersect externally at a point P. If PA = PC, Prove that AB = CD.
Solution:
Given: Two chords AB and CD intersect
each other at P outside the circle. PA = PC.

Question 35.
(a) In the figure (i) given below, AT is tangent to a circle at A. If ∠BAT = 45° and ∠BAC = 65°, find ∠ABC.

(b) In the figure (ii) given below, A, B and C are three points on a circle. The tangent at C meets BA produced at T. Given that ∠ATC = 36° and ∠ACT = 48°, calculate the angle subtended by AB at the centre of the circle. (2001)

Solution:
(a) AT is the tangent to the circle at A
and AB is the chord of the circle.

Question 36.
In the adjoining figure ∆ABC is isosceles with AB = AC. Prove that the tangent at A to the circumcircle of ∆ABC is parallel to BC.

Solution:
Given: ∆ABC is an isosceles triangle with AB = AC.
AT is the tangent to the circumcircle at A.

Question 37.
If the sides of a rectangle touch a circle, prove that the rectangle is a square.
Solution:
Given: A circle touches the sides AB, BC, CD and DA
of a rectangle ABCD at P, Q, R and S respectively.

To Prove : ABCD is a square.

Question 38.
(a) In the figure (i) given below, two circles intersect at A, B. From a point P on one of these circles, two line segments PAC and PBD are drawn, intersecting the other circle at C and D respectively. Prove that CD is parallel to the tangent at P.

(b) In the figure (ii) given below, two circles with centres C, C’ intersect at A, B and the point C lies on the circle with centre C’. PQ is a tangent to the circle with centre C’ at A. Prove that AC bisects ∠PAB.

Solution:
Given: Two circles intersect each other at A and B.
From a point P on one circle, PAC and PBD are drawn.
From P, PT is a tangent drawn. CD is joined.

Question 39.
(a) In the figure (i) given below, AB is a chord of the circle with centre O, BT is tangent to the circle. If ∠OAB = 32°, find the values of x and y.

(b) In the figure (ii) given below, O and O’ are centres of two circles touching each other externally at the point P. The common tangent at P meets a direct common tangent AB at M. Prove that:
(i) M bisects AB (ii) ∠APB = 90°.

Solution:
AB is a chord of a circle with centre O.
BT is a tangent to the circle and ∠OAB = 32°.
∴ In ∆OAB,
OA = OB (radii of the same circle)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 15 Circles Ex 15.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.