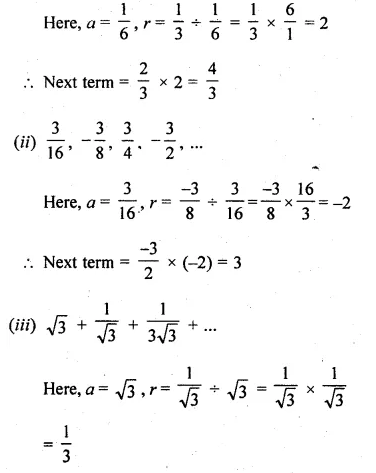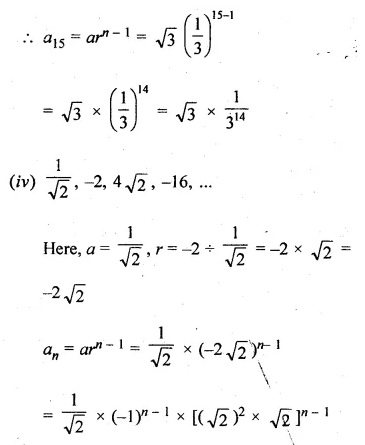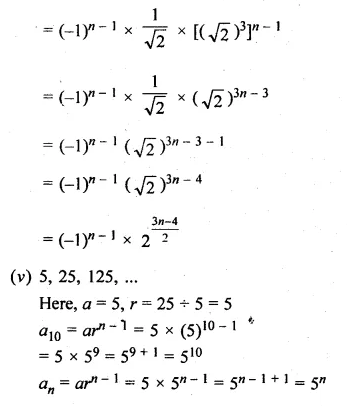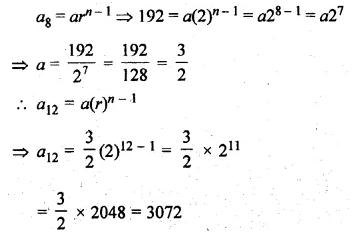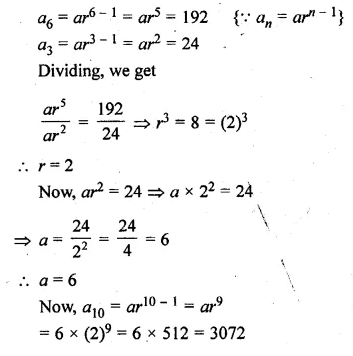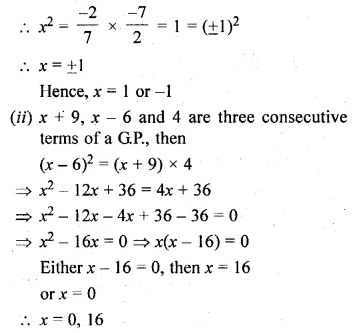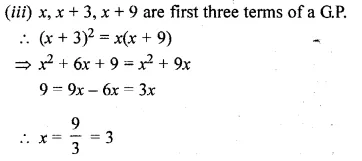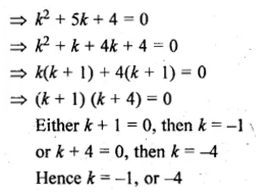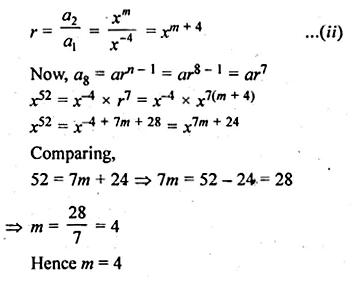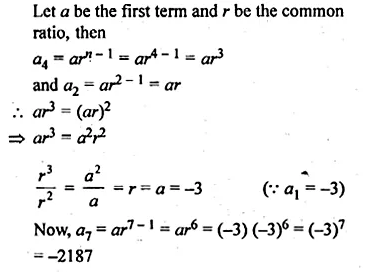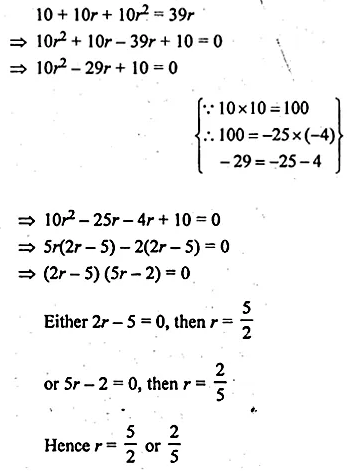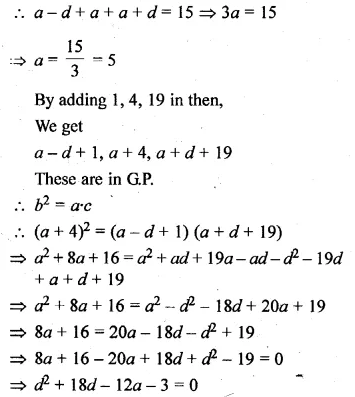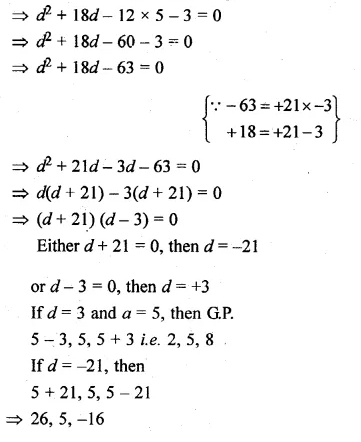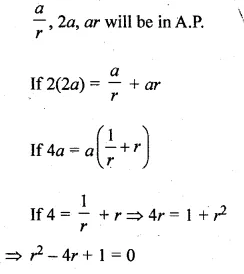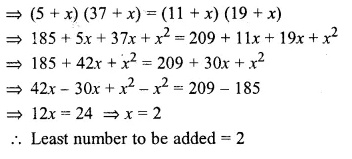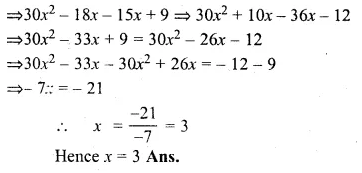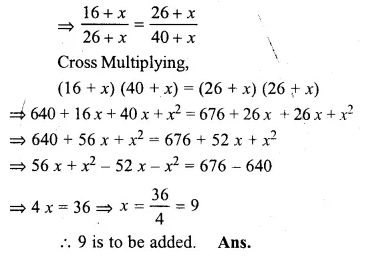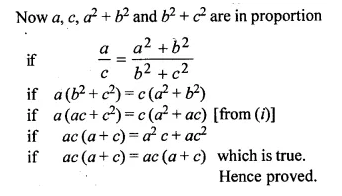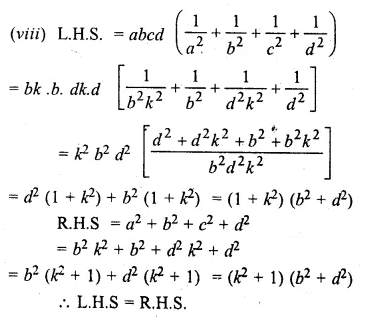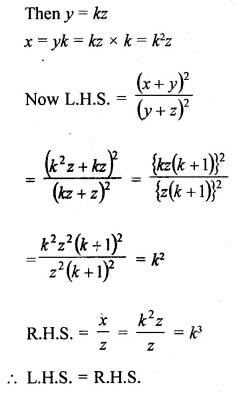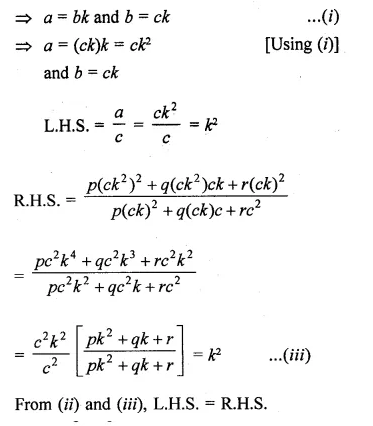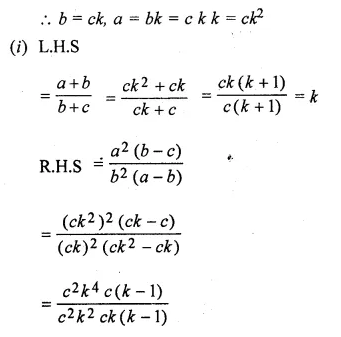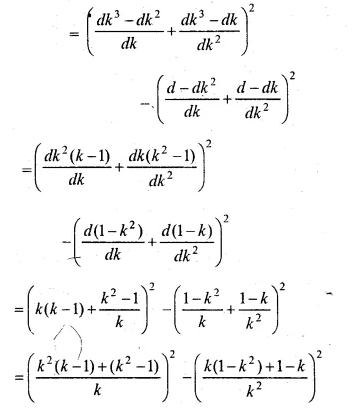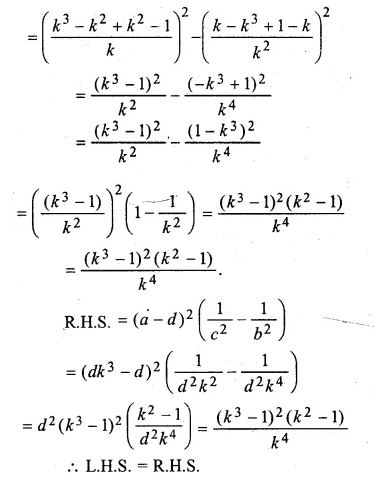Category: ICSE Class 10

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Find the sum of:
(i) 20 terms of the series 2 + 6 + 18 + …
(ii) 10 terms of series 1 + √3 + 3 + …
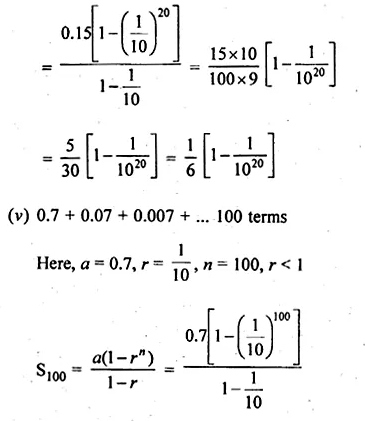
(iii) 6 terms of the GP. 1, \(– \frac { 2 }{ 3 } \) , \(\\ \frac { 4 }{ 9 } \), …
(iv) 20 terms of the GP. 0.15, 0.015, 0.0015,…
(v) 100 terms of the series 0.7 + 0.07 + 0.007 +…
(vi) 5 terms and n terms of the series \(1+\frac { 2 }{ 3 } +\frac { 4 }{ 9 } +…\)
(vii) n terms of the G.P. √7, √21, 3√7, …
(viii)n terms of the G.P. 1, – a, a², – a³, … (a ≠ – 1)
(ix) n terms of the G.P. x³, x⁵ , x⁷, … (x ≠ ±1).
Solution:
(i) 2 + 6 + 18 + … 20 terms
Here, a = 2, r = 3, n = 20, r > 1

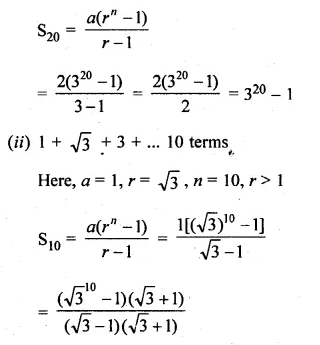
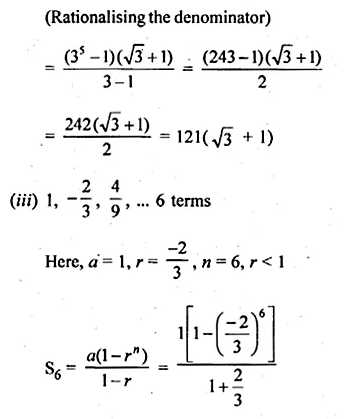
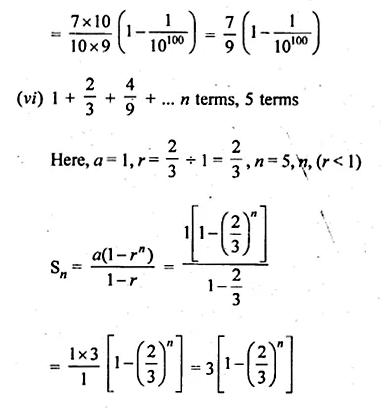
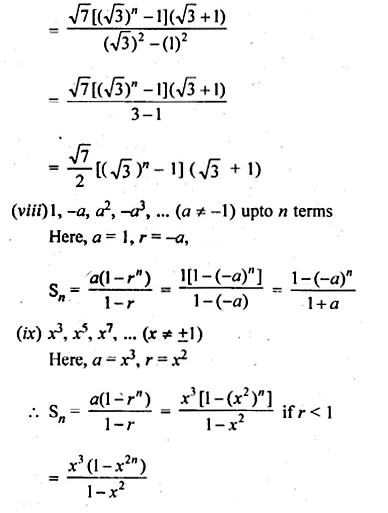
Question 2.
Find the sum of the first 10 terms of the geometric series
√2 + √6 + √18 + ….
Solution:
√2 + √6 + √18 + ….
Here, a = √2 , r = √3, r > 1

Question 3.
Find the sum of the series 81 – 27 + 9….\(– \frac { 1 }{ 27 } \)
Solution:
Given
81 – 27 + 9….\(– \frac { 1 }{ 27 } \)

Question 4.
The nth term of a G.P. is 128 and the sum of its n terms is 255. If its common ratio is 2, then find its first term.
Solution:
In a G.P.
T_n =128
S_n = 255
r = 2,
Let a be the first term, then

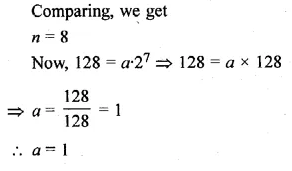
Question 5.
If the sum of first six terms of any G.P. is equal to 9 times the sum of the first three terms, then find the common ratio of the G.P.
Solution:
Sum of first 6 terms of a G.P. = 9 x The of first 3 terms
Let a be the first term and r be the common ratio

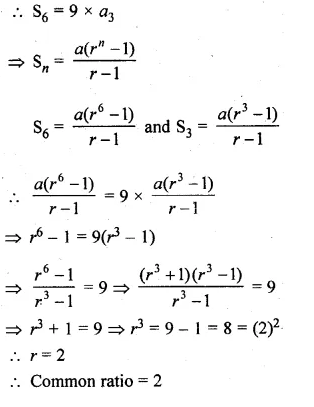
Question 6.
A G.P. consists of an even number of terms. If the sum of all the terms is 3 times the sum of the odd terms, then find its common ratio.
Solution:
Let the G.P. be a, ar, ar², … ar^{2n – 1}
These are 2n in number, which is an even number
A.T.Q.

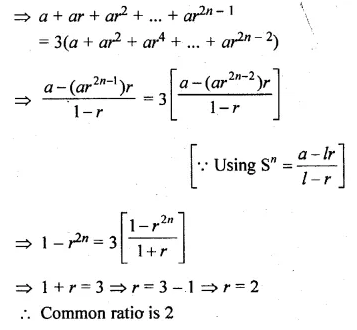
Question 7.
(i) How many terms of the G.P. 3, 3², 3³, … are needed to give the sum 120?
(ii) How many terms of the G.P. 1, 4, 16, … must be taken to have their sum equal to 341?
Solution:
In G.P.
(i) 3, 3², 3³, …
Sum = 120, Here, a = 3, r = \(\frac { { 3 }^{ 2 } }{ 3 } \) = 3, r > 1

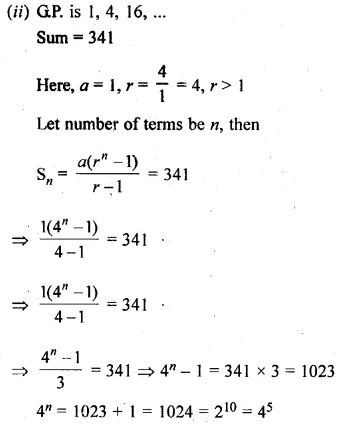
Question 8.
How many terms of the GP. 1, √2 > 2, 2 √2 , … are required to give a sum of 1023( √2 + 1)?
Solution:
GP. 1, √2 > 2, 2 √2 , …
Sum = 1023 (√2 + 1)
Here, a = 1, r = √2 . r > 1
Let number of terms be n, then

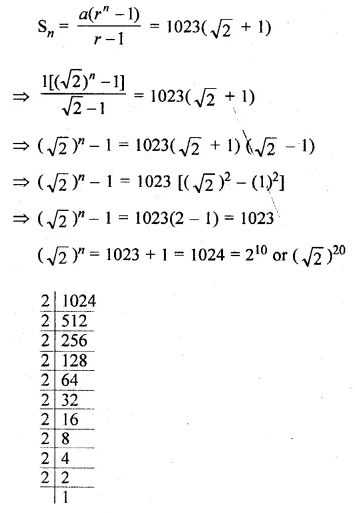
Question 9.
How many terms of the \(\frac { 2 }{ 9 } -\frac { 1 }{ 3 } +\frac { 1 }{ 2 } +…\) will make the sum \(\\ \frac { 55 }{ 72 } \) ?
Solution:
G.P. is \(\frac { 2 }{ 9 } -\frac { 1 }{ 3 } +\frac { 1 }{ 2 } +…\)
sum \(\\ \frac { 55 }{ 72 } \)

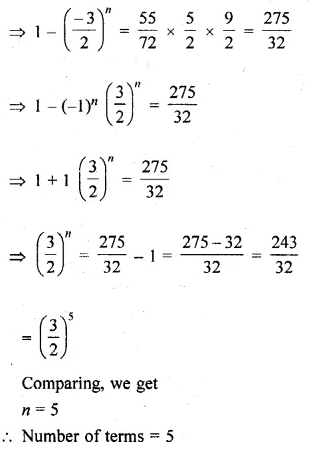
Question 10.
The 2nd and 5th terms of a geometric series are \(– \frac { 1 }{ 2 } \) and sum \(\\ \frac { 1 }{ 16 } \) respectively. Find the sum of the series upto 8 terms.
Solution:
In a G.P.
a₂ = \(– \frac { 1 }{ 2 } \) and a₅ = \(\\ \frac { 1 }{ 16 } \)
Let a be the first term and r be the common ratio

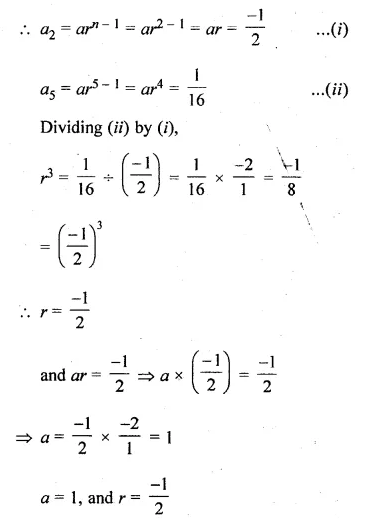
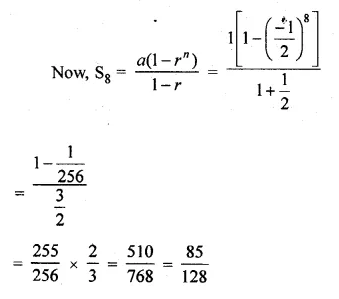
Question 11.
The first term of a G.P. is 27 and 8th term is \(\\ \frac { 1 }{ 81 } \) . Find the sum of its first 10 terms.
Solution:
In a G.P.
First term (a) = 27
a₈ = 81
Let r be the common ratio, then

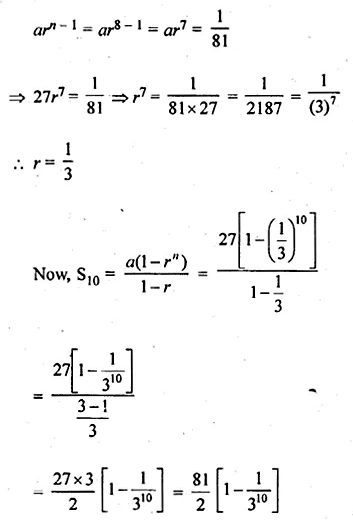
Question 12.
Find the first term of the G.P. whose common ratio is 3, last term is 486 and the sum of whose terms is 728
Solution:
Common ratio of a G.P. = 3
and last term = 486
and sum of terms = 728

Question 13.
In a G.P. the first term is 7, the last term is 448, and the sum is 889. Find the common ratio.
Solution:
In a GP.
First term (a) = 7, last term (l) = 448
and sum = 889
Let r be the common ratio, then

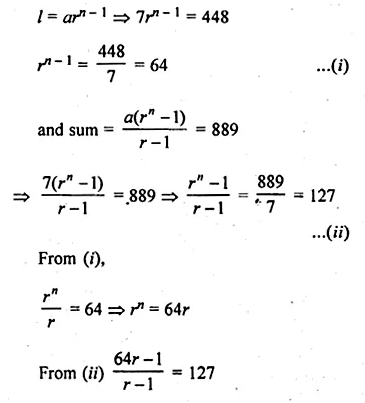
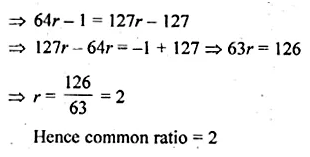
Question 14.
Find the third term of a G.P. whose common ratio is 3 and the sum of whose first seven terms is 2186.
Solution:
In a G.P.
Common ratio = 3

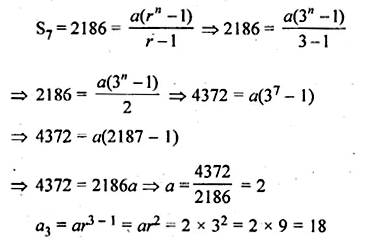
Question 15.
If the first term of a G.P. is 5 and the sum of first three terms is \(\\ \frac { 31 }{ 5 } \), find the common ratio.
Solution:
In a G.P.
First term (a) = 5

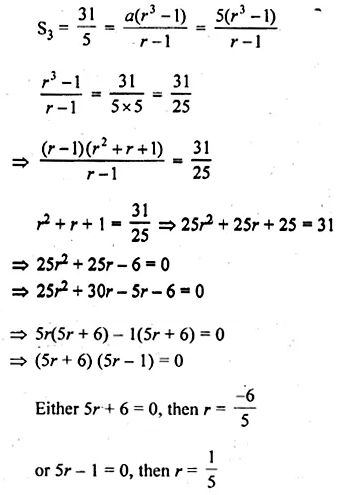
Question 16.
The sum of first three terms of a GP. is to the sum of first six terms as 125 : 152. Find the common ratio of the GP.
Solution:
S₃ ÷ S₆ = 125 : 152
Let r be the common ratio and a be the first number, then

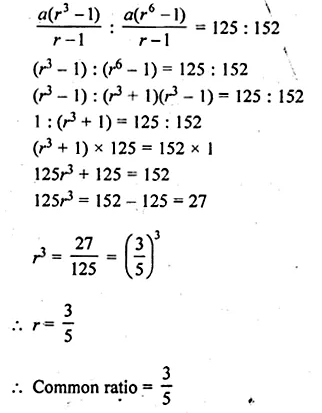
Question 17.
Find the sum of the products of the corresponding terms of the geometric progression 2, 4, 8, 16, 32 and 128, 32, 8, 2, \(\\ \frac { 1 }{ 2 } \)
Solution:
Sum of the product of corresponding terms of the G.M.s

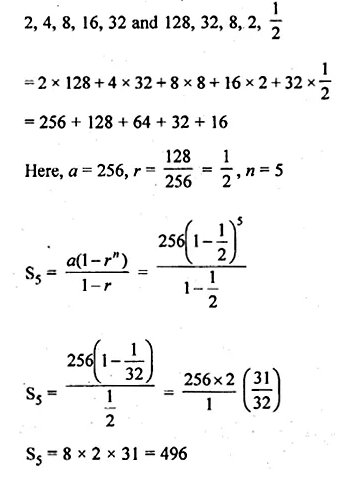
Question 18.
Evaluate \(\sum _{ n=1 }^{ 50 }{ \left( { 2 }^{ n }-1 \right) } \)
Solution:
\(\sum _{ n=1 }^{ 50 }{ \left( { 2 }^{ n }-1 \right) } \)
Here n = 1, 2, 3,….,50

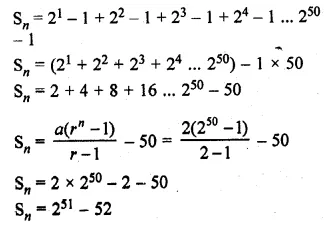
Question 19.
Find the sum of n terms of a series whose mth term is 2^m + 2m.
Solution:
a_m = 2^m + 2m
a₁ = 2¹ + 2 x 1 = 2 + 2

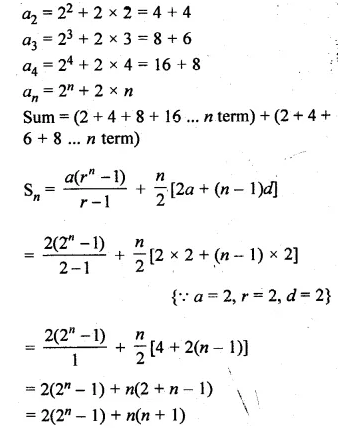
Question 20.
Sum the series
x(x + y) + x² (x² + y²) + x³ (x³ + y³) … to n terms.
Solution:
Given
S_n = x(x + y) + x² (x² + y²) + x³ (x³ + y³) … n terms

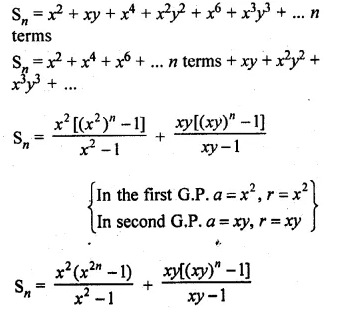
Question 21.
Find the sum of the series
1 + (1 + x) + (1 + x + x²) + … to n terms, x ≠ 1.
Solution:
1 + (1 + x) + (1 + x + x²) +… n terms, x ≠ 1
Multiply and divide by (1 – x)

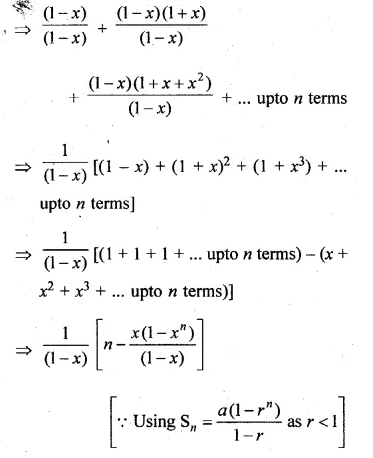
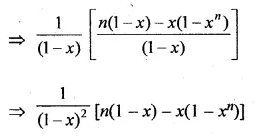
Question 22.
Find the sum of the following series to n terms:
(i) 7 + 77 + 777 + …
(ii) 8 + 88 + 888 + …
(iii) 0.5 + 0.55 + 0.555 + …
Solution:
(i) 7 + 77 + 777 + … n terms
= 7[1 + 11 + 111 + … n terms]

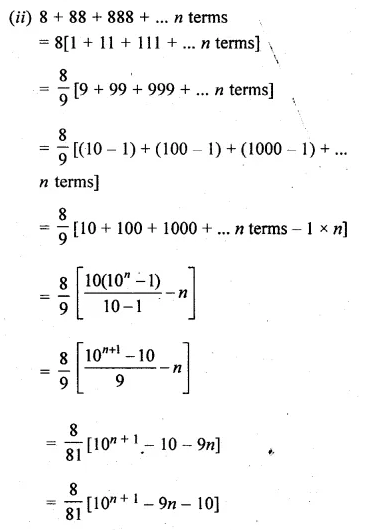
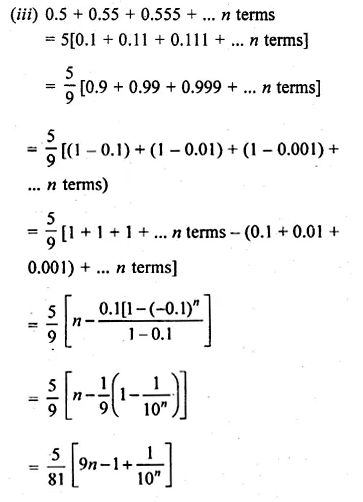
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test.

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

Question 1.
The point P (4, – 7) on reflection in x-axis is mapped onto P’. Then P’ on reflection in the y-axis is mapped onto P”. Find the co-ordinates of P’ and P”. Write down a single transformation that maps P onto P”.
Solution:
P’ is the image of P (4, -7) reflected in x-axis
∴ Co-ordinates of P’ are (4, 7)
Again P” is the image of P’ reflected in y-axis
∴ Co-ordinates of P” are (-4, 7)
∴ Single transformation that maps P and P” is in the origin.

Question 2.
The point P (a, b) is first reflected in the origin and then reflected in the y-axis to P’. If P’ has co-ordinates (3, – 4), evaluate a, b
Solution:
The co-ordinates of image of P(a, b) reflected in origin are (-a, -b).
Again the co-ordinates of P’, image of the above point (-a, -b)
reflected in the y-axis are (a, -b).
But co-ordinates of P’ are (3, -4)
∴a = 3 and -b = -4
b = 4 Hence a = 3, b = 4.

Question 3.
A point P (a, b) becomes ( – 2, c) after reflection in the x-axis, and P becomes (d, 5) after reflection in the origin. Find the values of a, b, c and d.
Solution:
If the image of P (a, b) after reflected in the x-axis be (a, -b) but it Is given (-2, c).
a = -2, c = -b
If P is reflected in the origin, then its co-ordinates will be (-a, -b), but it is given (d, 5)
∴ -b = 5 ⇒ b = -5
d = -a = -(-2) = 2, c = -b = -(-5) = 5
Hence a = -2, b = -5, c = 5, d = 2

Question 4.
A (4, – 1), B (0, 7) and C ( – 2, 5) are the vertices of a triangle. ∆ ABC is reflected in the y-axis and then reflected in the origin. Find the co-ordinates of the final images of the vertices.
Solution:
A (4, -1), B (0, 7) and C (-2, 5) are the vertices of ∆ABC.
After reflecting in y-axis, the co-ordinates of points will be
A’ (-4, -1), B’ (0, 7), C’ (2, 5). Again reflecting in origin,
the co-ordinates of the images of the vertices will be
A” (4, 1), B” (0, -7), C” (-2, -5)

Question 5.
The points A (4, – 11), B (5, 3), C (2, 15), and D (1, 1) are the vertices of a parallelogram. If the parallelogram is reflected in the y-axis and then in the origin, find the co-ordinates of the final images. Check whether it remains a parallelogram. Write down a single transformation that brings the above change.
Solution:
The points A (4, -11), B (5, 3), C (2, 15) and D (1, 1) are the vertices of a parallelogram.
After reflecting in/-axis, the images of these points will be
A’ ( -4, 11), B’ (-5, 3), C (-2, 15) and D’ (-1, 1).
Again reflecting these points in origin, the image of these points will be
A” (4, -11), B” (5, -3), C” (2, -15), D” (0, -1)
Yes, the reflection of a single transformation is in the x-axis.

Question 6.
Use a graph paper for this question (take 2 cm = 1 unit on both x and y axes).
(i) Plot the following points:
A (0, 4), B (2, 3), C (1, 1) and D (2, 0).
(ii) Reflect points B, C, D on 7-axis and write down their coordinates. Name the images as B’, C’, D’ respectively.
(iii) Join points A, B, C, D, D’, C’, B’ and A in order, so as to form a closed figure. Write down the equation of line of symmetry of the figure formed. (2017)
Solution:
(i) On graph A (0, 4), B (2, 3), C (1, 1) and D (2, 0)
(ii) B’ = (-2, 3), C’ = (-1, 1), D’ = (-2, 0)

The equation of the line of symmetry is x = 0

Question 7.
The triangle OAB is reflected in the origin O to triangle OA’B’. A’ and B’ have coordinates ( – 3, – 4) and (0, – 5) respectively.
(i) Find the co-ordinates of A and B.
(ii) Draw a diagram to represent the given information.
(iii) What kind of figure is the quadrilateral ABA’B’?
(iv) Find the coordinates of A”, the reflection of A in the origin followed by reflection in the y-axis.
(v) Find the co-ordinates of B”, the reflection of B in the x-axis followed by reflection in the origin.
Solution:
∆ OAB is reflected in the origin O to ∆ OA’B’,
Co-ordinates of A’ = (-3, -4), B’ (0, -5).
.’. Co-ordinates of A will be (3, 4) and of B will be (0, 5).
(ii) The diagram representing the given information has been drawn here.
(iii) The figure in the diagram is a rectangle.
(iv) The co-ordinates of B’, the reflection of B is the x-axis is (0, -5)
and co-ordinates of B”, the reflection in origin of the point (0, -5) will be (0, 5).
(v) The co-ordinates of the points, the reflection of A in the origin are (-3, -4)
and coordinates of A”, the reflected in y-axis of the point (-3, – 4) are (3, -4)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Choose the correct answer from the given four options (1 to 14) :

Question 1.
If A = [a_ij]_2×2 where a_ij = i + j, then A is equal to
(a) \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \)
(b) \(\begin{bmatrix} 2 & 3 \\ 3 & 4 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 2 \\ 1 & 2 \end{bmatrix} \)
(d) \(\begin{bmatrix} 1 & 1 \\ 2 & 2 \end{bmatrix} \)
Solution:
A = [a_ij]_2×2 where a_ij = i + j, then A is equal to
\(\begin{bmatrix} 2 & 3 \\ 3 & 4 \end{bmatrix} \) (b)

Question 2.
If \(\begin{bmatrix} x+3 & 4 \\ y-4 & x+y \end{bmatrix}=\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \) then the values of x and y are
(a) x = 2, y = 7
(b) x = 7, y = 2
(c) x = 3, y = 6
(d) x = – 2, y = 7
Solution:
\(\begin{bmatrix} x+3 & 4 \\ y-4 & x+y \end{bmatrix}=\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \)
Comparing we get
x + 3 = 5
⇒ x = 5 – 3 = 2
and y – 4 = 3
⇒ y = 3 + 4 = 7
x = 2, y = 7 (a)

Question 3.
If \(\begin{bmatrix} x+2y & -y \\ 3x & 7 \end{bmatrix}=\begin{bmatrix} -4 & 3 \\ 6 & 4 \end{bmatrix} \) then the values of x and y are
(a) x = 2, y = 3
(b) x = 2, y = – 3
(c) x = – 2, y = 3
(d) x = 3, y = 2
Solution:
\(\begin{bmatrix} x+2y & -y \\ 3x & 7 \end{bmatrix}=\begin{bmatrix} -4 & 3 \\ 6 & 4 \end{bmatrix} \)
Comparing, we get
3x = 6
⇒ \(x= \frac { 6 }{ 3 } \) = 2
⇒ -y = 3
⇒ y = – 3
x = 2, y = -3 (b)

Question 4.
If \(\begin{bmatrix} x-2y & 5 \\ 3 & y \end{bmatrix}=\begin{bmatrix} 6 & 5 \\ 3 & -2 \end{bmatrix} \) then the value of x is
(a) – 2
(b) 0
(c) 1
(d) 2
Solution:
\(\begin{bmatrix} x-2y & 5 \\ 3 & y \end{bmatrix}=\begin{bmatrix} 6 & 5 \\ 3 & -2 \end{bmatrix} \)
Comparing, we get
y = -2
and x – 2y = 6
⇒ x – 2 x (-2) = 6
⇒ x + 4 = 6
⇒ x = 6 – 4 = 2 (d)

Question 5.
If \(\begin{bmatrix} x+2y & 3y \\ 4x & 2 \end{bmatrix}=\begin{bmatrix} 0 & -3 \\ 8 & 2 \end{bmatrix} \) then the value of x – y is
(a) – 3
(b) 1
(c) 3
(d) 5
Solution:
\(\begin{bmatrix} x+2y & 3y \\ 4x & 2 \end{bmatrix}=\begin{bmatrix} 0 & -3 \\ 8 & 2 \end{bmatrix} \)
Comparing, we get
3y = -3
⇒ \(y= \frac { -3 }{ 3 } \) = -1
4x = 8
⇒ \(x= \frac { 8 }{ 4 } \) = 2
x – y = 2 – (-1) = 2 + 1 = 3 (c)

Question 6.
If \(x\left[ \begin{matrix} 2 \\ 3 \end{matrix} \right] +y\left[ \begin{matrix} -1 \\ 0 \end{matrix} \right] =\left[ \begin{matrix} 10 \\ 6 \end{matrix} \right] \) then the values of x and y are
(a) x = 2, y = 6
(b) x = 2, y = – 6
(c) x = 3, y = – 4
(d) x = 3, y = – 6
Solution:
Given
\(x\left[ \begin{matrix} 2 \\ 3 \end{matrix} \right] +y\left[ \begin{matrix} -1 \\ 0 \end{matrix} \right] =\left[ \begin{matrix} 10 \\ 6 \end{matrix} \right] \)

Question 7.
If B = \(\begin{bmatrix} -1 & 5 \\ 0 & 3 \end{bmatrix} \) and A – 2B = \(\begin{bmatrix} 0 & 4 \\ -7 & 5 \end{bmatrix} \)
then the matrix A is equal to
(a) \(\begin{bmatrix} 2 & 14 \\ -7 & 11 \end{bmatrix} \)
(b) \(\begin{bmatrix} -2 & 14 \\ 7 & 11 \end{bmatrix} \)
(c) \(\begin{bmatrix} 2 & -14 \\ 7 & 11 \end{bmatrix} \)
(d) \(\begin{bmatrix} -2 & 14 \\ -7 & 11 \end{bmatrix} \)
Solution:
Given
B = \(\begin{bmatrix} -1 & 5 \\ 0 & 3 \end{bmatrix} \) and
A – 2B = \(\begin{bmatrix} 0 & 4 \\ -7 & 5 \end{bmatrix} \)

Question 8.
If A + B = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \) and A – 2B = \(\begin{bmatrix} -1 & 1 \\ 0 & -1 \end{bmatrix} \)
then A is equal to
(a) \(\frac { 1 }{ 3 } \begin{bmatrix} 1 & 1 \\ 2 & 1 \end{bmatrix} \)
(b) \(\frac { 1 }{ 3 } \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 1 \\ 2 & 1 \end{bmatrix} \)
(d) \(\begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} \)
Solution:
A + B = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \) and
A – 2B = \(\begin{bmatrix} -1 & 1 \\ 0 & -1 \end{bmatrix} \)

Question 9.
A = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \) then A² =
(a) \(\begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix} \)
(b) \(\begin{bmatrix} 0 & 0 \\ 1 & 1 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)
(d) \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)
Solution:
Given
A = \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)

Question 10.
If A = \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \) , then A² =
(a) \(\begin{bmatrix} 1 & 1 \\ 0 & 0 \end{bmatrix} \)
(b) \(\begin{bmatrix} 0 & 0 \\ 1 & 1 \end{bmatrix} \)
(c) \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)
(d) \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \)
Solution:
Given
A = \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \)

Question 11.
If A = \(\begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} \) , then A² =
(a) A
(b) O
(c) I
(d) 2A
Solution:
Given
A = \(\begin{bmatrix} 0 & 0 \\ 1 & 0 \end{bmatrix} \)

Question 12.
If A = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \) , then A² =
(a) \(\begin{bmatrix} 2 & 0 \\ 1 & 1 \end{bmatrix} \)
(b) \(\begin{bmatrix} 1 & 0 \\ 1 & 2 \end{bmatrix} \)
(c) \(\begin{bmatrix} 1 & 0 \\ 2 & 1 \end{bmatrix} \)
(d) none of these
Solution:
Given
A = \(\begin{bmatrix} 1 & 0 \\ 1 & 1 \end{bmatrix} \)

Question 13.
If A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \) , then A² =
(a) \(\begin{bmatrix} 8 & 5 \\ -5 & 3 \end{bmatrix} \)
(b) \(\begin{bmatrix} 8 & -5 \\ 5 & 3 \end{bmatrix} \)
(c) \(\begin{bmatrix} 8 & -5 \\ -5 & -3 \end{bmatrix} \)
(d) \(\begin{bmatrix} 8 & -5 \\ -5 & 3 \end{bmatrix} \)
Solution:
A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \)
A² = A x A = \(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \)\(\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix} \)

Question 14.
If A = \(\begin{bmatrix} 2 & -2 \\ -2 & 2 \end{bmatrix} \) , then A² = pA, then the value of p is
(a) 2
(b) 4
(c) – 2
(d) – 4
Solution:
A = \(\begin{bmatrix} 2 & -2 \\ -2 & 2 \end{bmatrix} \)
and A² = pA

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

Choose the correct answer from the given four options (1 to 7) :

Question 1.
The reflection of the point P ( – 2, 3) in the x-axis is
(a) (2, 3)
(b) (2, – 3)
(c) ( – 2, – 3)
(d) ( – 2, 3)
Solution:
Reflection of the point P (-2, 3) in x-axis is (-2, -3) (c)

Question 2.
The reflection of the point P ( – 2, 3) in the y- axis is
(a) (2, 3)
(b) (2, – 3)
(c) ( – 2, – 3)
(d) (0, 3)
Solution:
The reflection of the point P (-2, 3) under reflection in y-axis (2, 3) (a)

Question 3.
If the image of the point P under reflection in the x-axis is ( – 3, 2), then the coordinates of the point P are
(a) (3, 2)
(b) ( – 3, – 2)
(c) (3, – 2)
(d) ( – 3, 0)
Solution:
The image of the point P under reflection in the x-axis is (-3, 2),
then the co-ordinates of the point P will be (-3, -2) (b)

Question 4.
The reflection of the point P (1, – 2) in the line y = – 1 is
(a) ( – 3, – 2)
(b) (1, – 4)
(c) (1 , 4)
(d) (1, 0)
Solution:
The reflection of the point P (1, -2) in the line y = -1 is (1, 0) (d)

Question 5.
The reflection of the point A (4, -1) in the line x = 2 is
(a) (0, – 1)
(b) (8, – 1)
(c) (0, 1)
(d) none of these
Solution:
The reflection of A (4, -1) in the line x = 2 will be A’ (0, -1) (a)

Question 6.
The reflection of the point ( – 3, 0) in the origin is the point
(a) (0, – 3)
(b) (0, 3)
(c) (3, 0)
(d) none of these
Solution:
Reflection of the point (-3, 0) in origin will be (3, 0) (c)

Question 7.
Which of the following points is invariant with respect to the line y = – 2 ?
(a) (3, 2)
(b) (3, – 2)
(c) (2, 3)
(d) ( – 2, 3)
Solution:
The variant points are (3, -2) (b)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Chapter Test

Question 1.
Can 0 be a term of a geometric progression?
Solution:
No, 0 is not a term of geometric progression.

Question 2.
(i) Find the next term of the list of numbers \(\frac { 1 }{ 6 } ,\frac { 1 }{ 3 } ,\frac { 2 }{ 3 } ,… \)
(ii) Find the next term of the list of numbers \(\frac { 3 }{ 16 } ,-\frac { 3 }{ 8 } ,\frac { 3 }{ 4 } ,-\frac { 3 }{ 2 } ,…\)
(iii) Find the 15th term of the series \(\sqrt { 3 } +\frac { 1 }{ \sqrt { 3 } } +\frac { 1 }{ 3\sqrt { 3 } } +…\)
(iv) Find the nth term of the list of numbers \(\frac { 1 }{ \sqrt { 2 } } ,-2,4\sqrt { 2 } ,-16,…\)
(v) Find the 10th and nth terms of the list of numbers 5, 25, 125, …
(vi) Find the 6th and the nth terms of the list of numbers \(\frac { 3 }{ 2 } ,\frac { 3 }{ 4 } ,\frac { 3 }{ 8 } ,…\)
(vii) Find the 6th term from the end of the list of numbers 3, – 6, 12, – 24, …, 12288.
Solution:
(i) Given
⇒ \(\frac { 1 }{ 6 } ,\frac { 1 }{ 3 } ,\frac { 2 }{ 3 } ,… \)

Question 3.
Which term of the G.P.
(i) 2, 2√2, 4, … is 128?
(ii) \(1,\frac { 1 }{ 3 } ,\frac { 1 }{ 9 } ,…is\quad \frac { 1 }{ 243 } ?\)
(iii) \(\frac { 1 }{ 3 } ,\frac { 1 }{ 9 } ,\frac { 1 }{ 27 } ,…is\quad \frac { 1 }{ 19683 } ? \)
Solution:
Given
(i) 2, 2√2, 4, … is 128?
Here a = 2, \(r=\frac { 2\sqrt { 2 } }{ 2 } =\sqrt { 2 } \), l = 128

Question 4.
Which term of the G.P. 3, – 3√3, 9, – 9√3, … is 729 ?
Solution:
G.P. 3, -3√3, 9, – 9√3, … is 729 ?
Here a = 3, \(r=\frac { -3\sqrt { 3 } }{ 3 } =\sqrt { -3 } \), l = 729

Question 5.
Determine the 12th term of a G.P. whose 8th term is 192 and common ratio is 2.
Solution:
In a G.P.
a₈ = 192 and r = 2
Let a be the first term and r be the common ratio then.

∴ a₁₂ = 3072

Question 6.
In a GP., the third term is 24 and 6th term is 192. Find the 10th term
Solution:
In a GP.
a₃ = 24 and a₆ = 192, a₁₀ = ?
Let a be the first term and r be the common ratio, therefore

Question 7.
Find the number of terms of a G.P. whose first term is \(\\ \frac { 3 }{ 4 } \), common ratio is 2 and the last term is 384.
Solution:
First term of a G.P. (a) = \(\\ \frac { 3 }{ 4 } \)
and common ratio (r) = 2
Last term = 384
Let number of terms is n

Question 8.
Find the value of x such that
(i) \(-\frac { 2 }{ 7 } ,x,-\frac { 7 }{ 2 } \) are three consecutive terms of a G.P.
(ii) x + 9, x – 6 and 4 are three consecutive terms of a G.P.
(iii) x, x + 3, x + 9 are first three terms of a G.P. Sol. Find the value of x
Solution:
Find the value of x
(i) \(-\frac { 2 }{ 7 } ,x,-\frac { 7 }{ 2 } \) are three consecutive terms of a G.P.

Question 9.
If the fourth, seventh and tenth terms of a G.P. are x, y, z respectively, prove that x, y, z are in G.P.
Solution:
In a G.P.
a₄ = x, a₇ = y, a₁₀ = z
To prove : x, y, z are in G.P.
Let a be the first term and r be the common

Question 10.
The 5th, 8th and 11th terms of a G.P. are p, q and s respectively. Show that q² = ps.
Solution:
In a G.P.
a₅ = p, a₈ = q and a₁₁ = s
To show that q² = px
Let a be the first term and r be the common

Question 11.
If a, b, c are in G.P., then show that a², b², c² are also in G.P.
Solution:
a, b, c are in G.P.
Show that a², b², c² are also in G.P
∵ a, b, c are in G.P., then
b² = ac …(i)
a², b², c² will be in G.P.
if (b²)² = a² x c²
⇒ (ac)² = a²c² [From (i)]
⇒ a²c² = a²c² which is true.
Hence proved.

Question 12.
If a, b, c are in A.P., then show that 3^a, 3^b, 3^c are in G.P.
Solution:
a, b and c are in A.P.
Then, 2b = a + c
Now, 3^a, 3^b, 3^c will be in G.P.
if (3^b)² = 3^a.3^c
if 3^2b = 3^a+c
Comparing, we get
if 2b = a + c
Which are in A.P. is given

Question 13.
If a, b, c are in A.P., then show that 10^{ax + 10}, 10^{bx + 10}, 10^{cx + 10}, x ≠ 0, are in G.P.
Solution:
a, b, c are in A.P.
To show that are in G.P.10^{ax + 10}, 10^{bx + 10}, 10^{cx + 10}, x ≠ 0
∵ a, b, c are in A.P.

Question 14.
If a, a²+ 2 and a³ + 10 are in G.P., then find the values(s) of a.
Solution:
a, a² + 2 and a³ + 10 are in G.P.
∵ (a² + 2)² = a(a³ + 10)

Question 15.
If k, 2k + 2, 3k + 3, … are in G.P., then find the common ratio of the G.P.
Solution:
k, 2k + 2, 3k + 3, … are in G.P.
then, (2k + 2)² = k(3k + 3)
⇒ 4k² + 8k + 4 = 3k² + 3k
⇒ 4k² + 8k + 4 – 3k² – 3k = 0

Question 16.
The first and the second terms of a GP. are x^-4 and x^m . If its 8th term is x⁵², then find the value of m.
Solution:
In a G.P.,
First term (a₁) = x^-4 …(i)
Second term (a₂) = x^m
Eighth term (a₈) = x⁵²

Question 17.
Find the geometric progression whose 4th term is 54 and the 7th Term is 1458.
Solution:
In a G.P.,
4th term (a₄) = 54

Question 18.
The fourth term of a GP. is the square of its second term and the first term is – 3. Determine its seventh term.
Solution:
In a GP.
a_n is square of a₂ i.e. an = (a₂)²
a₁ = – 3

Question 19.
The sum of first three terms of a G.P. is \(\\ \frac { 39 }{ 10 } \) and their product is 1. Find the common ratio and the terms.
Solution:
Sum of first three terms of G.P. = \(\\ \frac { 39 }{ 10 } \)
and their product = 1

Question 20.
Three numbers are in A.P. and their sum is 15. If 1, 4 and 19 are added to these numbers respectively, the resulting numbers are in G.P. Find the numbers.
Solution:
Given: Three numbers are in A.P. and their sum = 15
Let a – d, a, a + d be the three number in A.P.

Question 21.
Three numbers form an increasing G.P. If the middle term is doubled, then the new numbers are in A.P. Find the common ratio of the G.P.
Solution:
Three numbers form an increasing G.P.
Let \(\\ \frac { a }{ r } \) ,a,ar be three numbers in G.P.
Double the middle term, we get

Question 22.
Three numbers whose sum is 70 are in GP. If each of the extremes is multiplied by 4 and the mean by 5, the numbers will be in A.P. Find the numbers.
Solution:
Three numbers are in G.P.
Let numbers be
\(\\ \frac { r }{ a } \), a, ar

Question 23.
There are four numbers such that first three of them form an A.P. and the last three form a GP. The sum of the first and third number is 2 and that of second and fourth is 26. What are these numbers?
Solution:
There are 4 numbers, such that
First 3 numbers are in A.P. and
last 3 numbers are in GP.
Sum of first and third numbers = 2
and sum of 2nd and 4th = 26

Question 24.
(i) If a, b, c are in A.P. as well in G.P., prove that a = b = c.
(ii) If a, b, c are in A.P as well as in G.P., then find the value of a^b-c + b^c-a + c^a-b
Solution:
(i) a, b, c are in A.P. as well as in GP.
To prove: a = b = c
a, b, c are in A.P.

Question 25.
The terms of a G.P. with first term a and common ratio r are squared. Prove that resulting numbers form a G.P. Find its first term, common ratio and the nth term.
Solution:
In a G.P.,
The first term = a
and common ratio = r
GP. is a, ar, ar²
Squaring we get

Question 26.
Show that the products of the corresponding terms of two G.P.’s a, ar, ar², …, ar^n-1 and A, AR, AR², …, AR^n-1 form a G.P. and find the common ratio.
Solution:
It has to be proved that the sequence
aA, arAR, ar²AR², …, ar^n-1AR^n-1 and forms a G.P.

Question 27.
(i) If a, b, c are in G.P. show that \(\frac { 1 }{ a } ,\frac { 1 }{ b } ,\frac { 1 }{ c } \) are also in G.P.
(ii) If K is any positive real number and K^a, K^b K^c are three consecutive terms of a G.P., prove that a, b, c are three consecutive terms of an A.P.
(iii) If p, q, r are in A.P., show that pth, qth and rth terms of any G.P. are themselves in GP.
Solution:
(i) a, b, c are in G.P.
∴ b² = ac
\(\frac { 1 }{ a } ,\frac { 1 }{ b } ,\frac { 1 }{ c } \) will be in G.P.

Question 28.
If a, b, c are in GP., prove that the following are also in G.P.
(i) a³, b³, c³
(ii) a² + b², ab + bc, b² + c².
Solution:
(i) a, b, c are in G.P.
∴ b² = ac
a³, b³, c³ are in G.P.

Question 29.
If a, b, c, d are in G.P., show that
(i) a² + b², b² + c², c² + d² are in G.P.
(ii) (b – c)² + (c – a)² + (d – b)² = (a – d)².
Solution:
a, b, c, d are in G.P.
Let r be the common ratio, then a = a
b = ar, c = ar², d = ar³

Question 30.
The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour?
Solution:
Bacteria in the beginning = 30 = a
After every hours, it doubles itself
After 1 hour it becomes = 30 x 2 = 60 = ar
After 2 hours it will becomes = 60 x 2 = 120 = a²
After 3 hours, it will becomes = 120 x 2 = 240 = a³
After 4 hours it will becomes = 240 x 2 = 480 = a⁴
∴ After n hour, it will become = arⁿ

Question 31.
The length of the sides of a triangle form a G.P. If the perimeter of the triangle is 37 cm and the shortest side is of length 9 cm, find the lengths of the other two sides.
Solution:
Lengths of a triangle are in GP. and its sum is 37 cm
Let sides be a, ar, ar²
a + ar + ar² = 37
a = 9

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 9 Arithmetic and Geometric Progressions Ex 9.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Chapter Test

Question 1.
Find the co-ordinates of the images of the following points under reflection in the x- axis:
(i) (2, -5)
(ii) \(-\frac { 3 }{ 2 } ,-\frac { 1 }{ 2 } \)
(iii) ( – 7, 0)
Solution:
Co-ordinates of the images of the points
under reflection in the x-axis will be
(i) Image of (2, -5) will be (2, 5)
(ii) Image of \(-\frac { 3 }{ 2 } ,-\frac { 1 }{ 2 } \) will be \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of ( -7, 0) will be (-7, 0)

Question 2.
Find the co-ordinates of the images of the following points under reflection in the y-axis:
(i) (2, – 5)
(ii) \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) (0, – 7)
Solution:
Co-ordinates of the image of the points under reflection in the y-axis
(i) Image of (2, -5) will be ( -2, -5)
(ii) Image of \(-\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \) will be \(\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of (0, -7) will be (0, -7)

Question 3.
Find the co-ordinates of the images of the following points under reflection in the origin:
(i) (2, – 5)
(ii) \(\frac { -3 }{ 2 } ,\frac { -1 }{ 2 } \)
(iii) (0, 0)
Solution:
Co-ordinates of the image of the points under reflection in the y-axis
(i) Image of (2, -5) will be (-2, 5)
(ii) Image of \(\frac { -3 }{ 2 } ,\frac { -1 }{ 2 } \) will be \(\frac { 3 }{ 2 } ,\frac { 1 }{ 2 } \)
(iii) Image of (0, 0) will be (0, 0)

Question 4.
The image of a point P under reflection in the x-axis is (5, – 2). Write down the co-ordinates of P.
Solution:
As the image of a point (5, -2) under x – axis is P
∴ Co-ordinates of P will be (5, 2)

Question 5.
A point P is reflected in the x-axis. Co-ordinates of its image are (8, – 6).
(i) Find the co-ordinates of P.
(ii) Find the co-ordinates of the image of P under reflection in the y-axis.
Solution:
The co-ordinates of image of P which is reflected in x-axis are (8, – 6), then
(0 Co-ordinates of P will be (8, 6)
(ii) Co-ordinates of image of P under reflection in the y-axis will be ( – 8, 6)

Question 6.
A point P is reflected in the origin. Co-ordinates of its image are (2, – 5). Find
(i) the co-ordinates of P.
(ii) the co-ordinates of the image of P in the x-axis.
Solution:
The co-ordinates of image of a point P which is reflected in origin are (2, – 5), then
(i) Co-ordinates of P will be ( – 2, 5)
(ii) Co-ordinates of the image of P in the x- axis will be ( – 2, – 5)

Question 7.
(i) The point P (2, 3) is reflected in the line x = 4 to the point P’. Find the co-ordinates of the point P’.
(ii) Find the image of the point P (1, – 2) in the line x = – 1.
Solution:
(i) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit
(b) Plot point P (2, 3) on it.
(c) Draw a line x = 4 which is parallel to y-axis.
(d) From P, draw a perpendicular on x = 4, which intersects x = 4 at Q.
(e) Produce PQ to P’, such that QP’ = QP.
∴ P’ is the reflection of P in the line x = 4
Co-ordinates of P’ are (6, 3)

(ii) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot the point P (1, -2) on it.
(c) Draw a line x = -1 which is parallel toy-axis.
(d) From P, draw a perpendicular on the line x = -1, which meets it at Q.
(e) Produce PQ to P’ such that PQ = QP’
P’ is the image or reflection of P in the line x = -1
Co-ordinates of P’ are (-3, -2)
Co-ordinates of P’ are (-3, -2)

Question 8.
(i) The point P (2, 4) on reflection in the line y = 1 is mapped onto P’ Find the co-ordinates of P’.
(ii) Find the image of the point P ( – 3, – 5) in the line y = – 2.
Solution:
(i) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot point P (2, 4) on it.
(c) Draw a line y = 1, which is parallel to x-axis.
(d) From P, draw a perpendicular on y = 1 meeting it at Q.
(e) Produce PQ to P’ such that QP’ = PQ.
P’ is the reflection of P whose co-ordinates are (2, -2)

(ii) (a) Draw axis XOX’ and YOY’ and take 1 cm = 1 unit.
(b) Plot point P (-3, -5) on it.
(c) Draw a line y = -2 which is parallel to the x-axis.
(d) From P, draw a perpendicular on y = -2 which meets it at Q.
(e) Produce PQ to P’ such that QP’ = PQ.
Then P’ is the image of P, whose co-ordinates are (-3, 1).

Question 9.
The point P ( – 4, – 5) on reflection in y-axis is mapped on P’. The point P’ on reflection in the origin is mapped on P”. Find the co-ordinates of P’ and P”. Write down a single transformation that maps P onto P”.
Solution:
P’ is the image of point P (-4, -5) in y-axis
∴Co-ordinates of P’ will be (4, -5)
Again P” is the image of P’ under reflection in origin will be (-4, 5).
The single transformation that maps P onto P” is the x-axis

Question 10.
Write down the co-ordinates of the image of the point (3, – 2) when :
(i) reflected in the x-axis
(ii) reflected in the y-axis
(iii) reflected in the x-axis followed by reflection in the y-axis
(iv) reflected in the origin. (2000)
Solution:
Co-ordinates of the given points are (3, -2).
(i) Co-ordinates of the image reflected in x- axis will be (3, 2)
(ii) Co-ordinates of the image reflected in y- axis will be (-3, -2)
(iii) Co-ordinates of the point reflected in x- axis followed by reflection in the y-axis will be (-3, 2)
(iv) Co-ordinates of the point reflected in the origin will be (-3, 2)

Question 11.
Find the co-ordinates of the image of (3, 1) under reflection in x-axis followed by a reflection in the line x = 1.
Solution:
(i) Draw axis XOX’ and YOY’ taking 1 cm = 1 unit.
(ii) Plot a point P (3, 1).
(iii) Draw a line x = 1, which is parallel to y-axis.
(iv) From P, draw a perpendicular on x-axis meeting it at Q.
(v) Produce PQ to P’ such that QP’ = PQ, then
P’ is the image of P is x-axis. Then co-ordinates of P’ will be (3, -1)
(vi) From P’, draw a perpendicular on x = 1 meeting it at R.
(vii) Produce P’R to P” such that RP” = P’R
∴P” is the image of P’ in the line x = 1
Co-ordinates of P” are (-1, -1)

Question 12.
If P’ ( – 4, – 3) is the image of a point P under reflection in the origin, find
(i) the co-ordinates of P.
(ii) the co-ordinates of the image of P under reflection in the line y = – 2.
Solution:
(i) Reflection of P is P’ (-4, -3) in the origin
∴ Co-ordinates of P will be (4, 3)
Draw a line y = -2, which is parallel to x-axis
(ii) From P, draw a perpendicular on y = -2 meetings it at Q
Produce PQ to P” such that QP” = PQ
∴P” will the image of P in the line y = -2
∴Co-ordinates of P” will be (4, -7)

Question 13.
A Point P (a, b) is reflected in the x-axis to P’ (2, – 3), write down the values of a and b. P” is the image of P, when reflected in the y-axis. Write down the co-ordinates of P”. Find the co-ordinates of P”’, when P is reflected in the line parallel to y-axis such that x = 4. (1998)
Solution:
P’ (2, -3) is the reflection of P (a, b) in the x-axis
∴Co-ordinates of P’ will be P’ (a, – b) but P’ is (2, -3)
Comparing a = 2, b = 3

∴Co-ordinates of P will be (2, 3)
P” is the image of P when reflected in y-axis
∴Co-ordinate of P” will be ( – 2, 3)
Draw a line x = 4, which is parallel to y-axis
and P'” is the image of P when it is reflected in the line x = 4,
then P'” is its reflection Co-ordinates of P”‘ will be (6, 3).

Question 14.
(i) Point P (a, b) is reflected in the x-axis to P’ (5, – 2). Write down the values of a and b.
(ii) P” is the image of P when reflected in the y-axis. Write down the co-ordinates of P”.
(iii) Name a single transformation that maps P’ to P”. (1997)
Solution:
(i) Image of P (a, b) reflected in the x-axis to P’ (5, -2)
∴ a = 5 and b = 2
(ii) P” is the image of P when reflected in the y-axis
∴ its co-ordinates will be (-5, -2).
(iii) The single transformation that maps P’ to P” is the origin.

Question 15.
Points A and B have co-ordinates (2, 5) and (0, 3). Find
(i) the image A’ of A under reflection in the x-axis.
(ii) the image B’ of B under reflection in the line AA’.
Solution:
Co-ordinates of A are (2, 5) and of B are (0, 3)

(i) Co-ordinates of A’, the image of A reflected in the x-axis will be (2, -5)
(ii) Co-ordinates of B’, the image of B under reflection in the line AA’ will be (4, 3).

Question 16.
Plot the points A (2, – 3), B ( – 1, 2) and C (0, – 2) on the graph paper. Draw the triangle formed by reflecting these points in the x-axis. Are the two triangles congruent?

Solution:
The points A (2, -3), B (-1, 2) and C(0, -2) has been plotted on the graph paper as shown and are joined to form a triangle ABC. The co-ordinates of the images of A, B and C reflected in x-axis will be A’ (2, 3), B’ (-1, -2), C’ (0, 2) respectively and are joined to from another ∆ A’B’C’
Yes, these two triangles are congruent.

Question 17.
The points (6, 2), (3, – 1) and ( – 2, 4) are the vertices of a right angled triangle. Check whether it remains a right angled triangle after reflection in the y-axis.
Solution:
Let A (6, 2), B (3, -1) and C (-2, 4) be the points of a right-angled triangle
then the co-ordinates of the images of A, B, C reflected in y-axis be
A’ (-6, 2), B’ (-3, -1) and C’ (2, 4).

By joining these points, we find that ∆A’B’C’ is also a right angled triangle.

Question 18.
The triangle ABC where A (1, 2), B (4, 8), C (6, 8) is reflected in the x-axis to triangle A’ B’ C’. The triangle A’ B’ C’ is then reflected in.the origin to triangle A”B”C” Write down the co-ordinates of A”, B”, C”. Write down a single transformation that maps ABC onto A” B” C”.
Solution:
The co-ordinates of ∆ ABC are A (1, 2) B (4, 8), C (6, 8)
which are reflected in x- axis as A’, B’ and C’.
∴ The co-ordinates of A’ (1, -2), B (4, -8) and C (6, -8).
A’, B’ and C’ are again reflected in origins to form an ∆A”B”C”.
∴ The co-ordinates of A” will be (-1, 2), B” (-4, 8) and C” (-6, 8)
The single transformation that maps ABC onto A” B” C” is y-axis.

Question 19.
The image of a point P on reflection in a line l is point P’. Describe the location of the line l.
Solution:
The line will be the right bisector of the line segment joining P and P’.

Question 20.
Given two points P and Q, and that (1) the image of P on reflection in y-axis is the point Q and (2) the mid point of PQ is invariant on reflection in x-axis. Locate
(i) the x-axis
(ii) the y-axis and
(iii) the origin.
Solution:
Q is the image of P on reflection in y-axis
and mid point of PQ is invariant on reflection in x-axis

(i) x-axis will be the line joining the points P and Q.
(ii) The line perpendicular bisector of line segment PQ is the y-axis.
(iii) The origin will be the mid point of line segment PQ.

Question 21.
The point ( – 3, 0) on reflection in a line is mapped as (3, 0) and the point (2, – 3) on reflection in the same line is mapped as ( – 2, – 3).
(i) Name the mirror line.
(ii) Write the co-ordinates of the image of ( – 3, – 4) in the mirror line.
Solution:
The point (-3,0) is the image of point (3, 0)
and point (2, -3) is image of point (-2, -3) reflected on the same line.
(i) It is clear that the mirror line will be y-axis.
(ii) The co-ordinates of the image of the point (-3, -4)
reflected in the same line i.e. y-axis will be (3, -4).

Question 22.
A ( – 2, 4) and B ( – 4, 2) are reflected in the y-axis. If A’ and B’ are images of A and B respectively, find

(i) the co-ordinates of A’ and B’.
(ii) Assign special name to quad. AA’B’B.
(iii) State whether AB’ = BA’.
Solution:
A (-2, 4) and B (-4, 2) are reflected in y- axis as A’ and B’.

(i) Co-ordinates of A’ are (2, 4) and of B are (4, 2).
(ii) The quadrilateral AA’ B’ B is an isosceles trapezium.
(iii) yes, AB’ = BA’

Question 23.
Use graph paper for this question.
(i) The point P (2, – 4) is reflected about the line x = 0 to get the image Q. Find the co-ordinates of Q.
(ii) Point Q is reflected about the line y = 0 to get the image R. Find the co-ordinates of R.
(iii) Name the figure PQR.
(iv) Find the area of figure PQR. (2007)
Solution:
(i) Since the point Q is the reflection of the point P (2, -4) in the line x = 0,
the co-ordinates of Q are (2, 4).
(ii) Since R is the reflection of Q (2, 4) about the line y = 0,
the co-ordinates of R are ( – 2, 4).
(iii) Figure PQR is the right angled triangle PQR.

(iv) Area of ∆ PQR = \(\\ \frac { 1 }{ 2 } \) x QR x PQ
= \(\\ \frac { 1 }{ 2 } \) x 4 x 8
= 16 sq. units.

Question 24.
Use graph paper for this question. The point P (5, 3) was reflected in the origin to get the image P’.
(i) Write down the co-ordinates of P’.
(ii) If M is the foot of perpendicular from P to the x-axis, find the co-ordinates of M.
(iii) If N is the foot of the perpendicular from P’ to the x-axis, find the co-ordinates of N.
(iv) Name the figure PMP’N.
(v) Find the area of the figure PMP’N. (2001)
Solution:
P’ is the image of point P (5, 3) reflected in the origin.

(i) Co-ordinates of P’ will be (-5, -3).
(ii) M is the foot of the perpendicular from P to the x-axis.
Co-ordinates of M will be (5, 0)
(iii) N is the foot of the perpendicular from P’ to x-axis.
Co-ordinates of N will be (-5, 0).
(iv) By joining the points, the figure PMP’N is a parallelogram.
(v) Area of the parallelogram = 2 x area of ∆ MPN
= 2 x \(\\ \frac { 1 }{ 2 } \) x MN x PM = MN x PM
= 10 x 3 = 30 sq. units. Ans.

Question 25.
Using a graph paper, plot the points A (6, 4) and B (0, 4).
(i) Reflect A and B in the origin to get the images A’ and B’.
(ii) Write the co-ordinates of A’ and B’.
(iii) State the geometrical name for the figure ABA’B’.
(iv) Find its perimeter.
Solution:
(i) A (6, 4), B (0, 4)

Perimeter = Sum of all sides = 6 + 10 + 6 + 10 = 32 units

Question 26.
Use graph paper to answer this question
(i) Plot the points A (4, 6) and B (1, 2).
(ii) If A’ is the image of A when reflected in x-axis, write the co-ordinates of A’.
(iii) If B’ is the image of B when B is reflected in the line AA’, write the co-ordinates of B’.
(iv) Give the geometrical name for the figure ABA’B’. (2009)
Solution:
(i) Plotting the points A (4, 6) and B (1, 2) on the given graph.
(ii) A’ = (4, -6)
(iii) B’ = (7, 2)
(iv) In the quadrilateral ABA’B’, we have AB = AB’ and A’B = A’B’
Hence, ABA’B’ is a kite.

Question 27.
The points A (2, 3), B (4, 5) and C (7, 2) are the vertices’s of ∆ABC. (2006)
(i) Write down the co-ordinates of A1, B1, C1 if ∆ A1B1C1 is the image of ∆ ABC when reflected in the origin.
(ii) Write down the co-ordinates of A2, B2, C2 if ∆ A2B2C2 is the image of ∆ ABC when reflected in the x-axis.
(iii) Assign the special name to the quadrilateral BCC2B2 and find its area.


Solution:
Points A (2, 3), B (4, 5) and C (7, 2) are the vertices’s of ∆ ABC.
A1, B1 and C1 are the images of A, B and C reflected in the origin.
(i) Co-ordinates of A1 = (-2, -3) of B1 (-4, -5) and of C1 (-7, -2).
(ii) Co-ordinates of A2, B2 and C2 the images of A, B and C
when reflected in x-axis are A2 (2, – 3), B2 (4, – 5), C2 (7, – 2)
(iii) The quadrilateral formed by joining the points,
BCC2B2 is an isosceles trapezium and its area

Question 28.
The point P (3, 4) is reflected to P’ in the x-axis and O’ is the image of O (origin) in the line PP’. Find :
(i) the co-ordinates of P’ and O’,
(ii) the length of segments PP’ and OO’.
(iii) the perimeter of the quadrilateral POP’O’.
Solution:
P’ is the image of P (3, 4) reflected in x- axis
and O’ is the image of O the origin in the line P’P.
(i) Co-ordinates of P’ are (3, -4)
and co-ordinates of O’ reflected in PP’ are (6, 0)
(ii) Length of PP’ = 8 units and OO’ = 6 units
(iii) Perimeter of POP’O’ is

Question 29.
Use a graph paper for this question. (Take 10 small divisions = 1 unit on both axes). P and Q have co-ordinates (0, 5) and ( – 2, 4).
(i) P is invariant when reflected in an axis. Name the axis.
(ii) Find the image of Q on reflection in the axis found in (i).
(iii) (0, k) on reflection in the origin is invariant. Write the value of k.
(iv) Write the co-ordinates of the image of Q, obtained by reflecting it in the origin followed by reflection in x-axis. (2005)
Solution:

(i) Two points P (0, 5) and Q (-2, 4) are given As the abscissa of P is 0.
It is invariant when is reflected in y-axis.
(ii) Let Q’ be the image of Q on reflection in y-axis.
Co-ordinate of Q’ will be (2, 4)
(iii) (0, k) on reflection in the origin is invariant.
co-ordinates of image will be (0, 0). k = 0
(iv) The reflection of Q in the origin is the point Q”
and its co-ordinates will be (2, – 4)
and reflection of Q” (2, – 4) in x-axis is (2, 4) which is the point Q’

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 10 Reflection Ex 10 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test

Question 1.
Check whether the following are quadratic equations:
(i)\(\sqrt { 3 } { x }^{ 2 }-2x+\frac { 3 }{ 5 } =0\)
(ii)(2x + 1) (3x – 2) = 6(x + 1) (x – 2)
(iii)\({ (x-3) }^{ 3 }+5={ x }^{ 3 }+7{ x }^{ 2 }-1\)
(iv)\(x-\frac { 3 }{ x } =2,x\neq 0\)
(v)\(x+\frac { 2 }{ x } ={ x }^{ 2 },x\neq 0\)
(vi)\({ x }^{ 2 }+\frac { 1 }{ { x }^{ 2 } } =3,x\neq 0 \)
Solution:
(i) \(\sqrt { 3 } { x }^{ 2 }-2x+\frac { 3 }{ 5 } =0\)
It is a quadratic equation as it is power of 2.
(ii) (2x + 1) (3x – 2) = 6(x + 1) (x – 2)
6x² – 4x + 3x – 2 = 6(x² – 2x + x – 2)
6x² – x – 2 = 6x² – 12x + 6x – 12

Question 2.
In each of the following, determine whether the given numbers are roots of the given equations or not;
(i) x² – x + 1 = 0; 1, – 1
(ii) x² – 5x + 6 = 0; 2, – 3
(iii) 3x² – 13x – 10 = 0; 5,\(\\ \frac { -2 }{ 3 } \)
(iv) 6x² – x – 2 = 0;\(\\ \frac { -1 }{ 2 } \), \(\\ \frac { 2 }{ 3 } \)
Solution:
(i) x² – x + 1 = 0; 1, -1
Where x = 1, then
(1)² – 1 + 1 = 1 – 1 + 1 = 1 ≠ 0
∴ x = 1 does not satisfy it

Question 3.
In each of the following, determine whether the given numbers are solutions of the given equation or not:
(i) x² – 3√3x + 6 = 0; √3, – 2√3
(ii) x² – √2x – 4 = 0, x = – √2, 2√2
Solution:
(i) x² – 3√3x + 6 = 0; √3, -2√3
(a) Substituting the value of x = √3

Question 4.
(i) If \(– \frac { 1 }{ 2 } \) is a solution of the equation 3x² + 2kx – 3 = 0, find the value of k.
(ii) If \(\\ \frac { 2 }{ 3 } \) is a solution of the equation 7x² + kx – 3 = 0, find the value of k.
Solution:
(i) x = \(– \frac { 1 }{ 2 } \) is a solution of the
3x² + 2kx – 3 = 0,
Substituting the value of x in the given equation

Question 5.
(i) If √2 is a root of the equation kx² + √2 – 4 = 0, find the value of k.
(ii) If a is a root of the equation x² – (a + b)x + k = 0, find the value of k.
Solution:
(i) kx² + √2 – 4 = 0, x = √2
x = √2 is its solution

Question 6.
If \(\\ \frac { 2 }{ 3 } \) and – 3 are the roots of the equation px² + 7x + q = 0, find the values of p and q.
Solution:
\(\\ \frac { 2 }{ 3 } \) and – 3 are the roots of the equation px² + 7x + q = 0
Substituting the value of x = \(\\ \frac { 2 }{ 3 } \) and – 3 respectively, we get

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test

Choose the correct answer from the given four options (1 to 15) :

Question 1.
Which of the following is not a quadratic equation ?
(a) (x + 2)² = 2(x + 3)
(b) x² + 3x = ( – 1) (1 – 3x)
(c) (x + 2) (x – 1) = x² – 2x – 3
(d) x³ – x² + 2x + 1 = (x + 1)³
Solution:
(a) (x + 2)² = 2(x + 3)
⇒ x² + 4x + 4 = 2x + 6
⇒ x² + 4x – 2x + 4 – 6 = 0
⇒ x² + 2x – 2
It is a quadratic equation.

Question 2.
Which of the following is a quadratic equation ?
(a) (x – 2) (x + 1) = (x – 1) (x – 3)
(b) (x + 2)³ = 2x(x² – 1)
(c) x² + 3x + 1 = (x – 2)²
(d) 8(x – 2)³ = (2x – 1)³ + 3
Solution:
(a) (x – 2) (x + 1) = (x – 1) (x – 3)
⇒ x² + x – 2x – 2 = x² – 3x – x + 3
⇒ 3x + x – 2x + x = 3 + 2
⇒ 3x = 5
It is not a quadratic equation.

Question 3.
Which of the following equations has 2 as a root ?
(a) x² – 4x + 5 = 0
(b) x² + 3x – 12 = 0
(c) 2x² – 7x + 6 = 0
(d) 3x² – 6x – 2 = 0
Solution:
(a) x² – 4x + 5 = 0
⇒ (2)² – 4x² + 5 = 0
⇒ 4 – 8 + 5 = 0
⇒ 9 – 8 ≠ 0
2 is not its root.

Question 4.
If \(\\ \frac { 1 }{ 2 } \) is a root of the equation x² + kx – \(\\ \frac { 5 }{ 4 } \) = 0, then the value of k is
(a) 2
(b) – 2
(c) \(\\ \frac { 1 }{ 4 } \)
(d) \(\\ \frac { 1 }{ 2 } \)
Solution:
\(\\ \frac { 1 }{ 2 } \) is a root of the equation
x² + kx – \(\\ \frac { 5 }{ 4 } \) = 0
Substituting the value of x = \(\\ \frac { 1 }{ 2 } \) in the

Question 5.
If \(\\ \frac { 1 }{ 2 } \) is a root of the quadratic equation 4x² – 4kx + k + 5 = 0, then the value of k is
(a) – 6
(b) – 3
(c) 3
(d) 6
Solution:
\(\\ \frac { 1 }{ 2 } \) is a root of the equation
4x² – 4kx + k + 5 = 0

Question 6.
The roots of the equation x² – 3x – 10 = 0 are
(a) 2,- 5
(b) – 2, 5
(c) 2, 5
(d) – 2, – 5
Solution:
x² – 3x – 10 = 0

x = 5, – 2 or – 2, 5 (b)

Question 7.
If one root of a quadratic equation with rational coefficients is \(\frac { 3-\sqrt { 5 } }{ 2 } \), then the other
(a)\(\frac { -3-\sqrt { 5 } }{ 2 } \)
(b)\(\frac { -3+\sqrt { 5 } }{ 2 } \)
(c)\(\frac { 3+\sqrt { 5 } }{ 2 } \)
(d)\(\frac { \sqrt { 3 } +5 }{ 2 } \)
Solution:
One root of a quadratic equation is \(\frac { 3-\sqrt { 5 } }{ 2 } \)
then other root will be \(\frac { 3+\sqrt { 5 } }{ 2 } \) (c)

Question 8.
If the equation 2x² – 5x + (k + 3) = 0 has equal roots then the value of k is
(a)\(\\ \frac { 9 }{ 8 } \)
(b)\(– \frac { 9 }{ 8 } \)
(c)\(\\ \frac { 1 }{ 8 } \)
(d)\(– \frac { 1 }{ 8 } \)
Solution:
2x² – 5x + (k + 3) = 0
a = 2, b = -5, c = k + 3

Question 9.
The value(s) of k for which the quadratic equation 2x² – kx + k = 0 has equal roots is (are)
(a) 0 only
(b) 4
(c) 8 only
(d) 0, 8
Solution:
2x² – kx + k = 0
a = 2, b = -k, c = k

Question 10.
If the equation 3x² – kx + 2k =0 roots, then the the value(s) of k is (are)
(a) 6
(b) 0 Only
(c) 24 only
(d) 0
Solution:
3x² – kx + 2k = 0
Here, a = 3, b = -k, c = 2k

Question 11.
If the equation {k + 1)x² – 2(k – 1)x + 1 = 0 has equal roots, then the values of k are
(a) 1, 3
(b) 0, 3
(c) 0, 1
(d) 0, 1
Solution:
(k + 1)x² – 2(k – 1)x + 1 = 0
Here, a = k + 1, b = -2(k – 1), c = 1

k = 0, 3 (b)

Question 12.
If the equation 2x² – 6x + p = 0 has real and different roots, then the values ofp are given by
(a)p < \(\\ \frac { 9 }{ 2 } \)
(b)p ≤ \(\\ \frac { 9 }{ 2 } \)
(c)p > \(\\ \frac { 9 }{ 2 } \)
(d)p ≥ \(\\ \frac { 9 }{ 2 } \)
Solution:
2x² – 6x + p = 0
Here, a = 2, b = -6, c = p

Question 13.
The quadratic equation 2x² – √5x + 1 = 0 has
(a) two distinct real roots
(b) two equal real roots
(c) no real roots
(d) more than two real roots
Solution:
2x² – √5x + 1 = 0
Here, a = 2, b = -√5, c = 1

Question 14.
Which of the following equations has two distinct real roots ?
(a) 2x² – 3√2x + \(\\ \frac { 9 }{ 4 } \) = 0
(b) x² + x – 5 = 0
(c) x² + 3x + 2√2 = 0
(d) 5x² – 3x + 1 = 0
Solution:
(a) 2x² – 3√2x + \(\\ \frac { 9 }{ 4 } \) = 0
b² – 4ac = ( -3√2)² – 4 x 2 x \(\\ \frac { 9 }{ 4 } \) = 18 – 18 = 0
.’. Roots are real and equal.

Question 15.
Which of the following equations has no real roots ?
(a) x² – 4x + 3√2 = 0
(b) x² + 4x – 3√2 = 0
(c) x² – 4x – 3√2 = 0
(d) 3x² + 4√3x + 4 = 0
Solution:
(a) x² – 4x + 3√2 = 0
b² – 4ac = ( -4)² – 4 × 1 × 3√2
= 16 – 12√2
= 16 – 12(1.4)
= 16 – 16.8
= -0.8
b² – 4ac < 0
Roots are not real. (a)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Chapter Test

Question 1.
Find the value of x in the following proportions :
(i) 10 : 35 = x : 42
(ii) 3 : x = 24 : 2
(iii) 2.5 : 1.5 = x : 3
(iv) x : 50 :: 3 : 2
Solution:
(i) 10 : 35 = x : 42
⇒ 35 × x = 10 × 42

Question 2.
Find the fourth proportional to
(i) 3, 12, 15
(ii) \(\frac { 1 }{ 3 } ,\frac { 1 }{ 4 } ,\frac { 1 }{ 5 } \)
(iii) 1.5, 2.5, 4.5
(iv) 9.6 kg, 7.2 kg, 28.8 kg
Solution:
(i) Let fourth proportional to
3, 12, 15 be x.
then 3 : 12 :: 15 : x

Question 3.
Find the third proportional to
(i) 5, 10
(ii) 0.24, 0.6
(iii) Rs. 3, Rs. 12
(iv) \(5 \frac { 1 }{ 4 } \) and 7.
Solution:
(i) Let x be the third proportional to 5, 10,
then 5 : 10 :: 10 : x

Question 4.
Find the mean proportion of:
(i) 5 and 80
(ii) \(\\ \frac { 1 }{ 12 } \) and \(\\ \frac { 1 }{ 75 } \)
(iii) 8.1 and 2.5
(iv) (a – b) and (a³ – a²b), a> b
Solution:
(i) Let x be the mean proportion of 5 and 80 ,
then 5 : x : : x : 80
x² = 5 x 80
⇒ x = \(\sqrt { 5\times 80 } =\sqrt { 400 } \) = 20
x = 20

Question 5.
If a, 12, 16 and b are in continued proportion find a and b.
Solution:
∵ a, 12, 16, b are in continued proportion, then

Question 6.
What number must be added to each of the numbers 5, 11, 19 and 37 so that they are in proportion ? (2009)
Solution:
Let x be added to 5, 11, 19 and 37 to make them in proportion.
5 + x : 11 + x : : 19 + x : 37 + x

Question 7.
What number should be subtracted from each of the numbers 23, 30, 57 and 78 so that the remainders are in proportion ? (2004)
Solution:
Let x be subtracted from each term, then
23 – x, 30 – x, 57 – x and 78 – x are proportional
23 – x : 30 – x : : 57 – x : 78 – x

Question 8.
If 2x – 1, 5x – 6, 6x + 2 and 15x – 9 are in proportion, find the value of x.
Solution:
∵ 2x – 1, 5x – 6, 6x + 2 and 15x – 9 are in proportion.
then (2x – 1) (15x – 9) = (5x – 6) (6x + 2)

Question 9.
If x + 5 is the mean proportion between x + 2 and x + 9, find the value of x.
Solution:
∵ x + 5 is the mean proportion between x + 2 and x + 9, then
(x + 5)² = (x + 2) (x + 9)
⇒ x² + 10x + 25 = x² + 11x + 18
⇒ x² + 10x – x² – 11x = 18 – 25
⇒ – x = – 7
∵ x = 7 Ans.

Question 10.
What number must be added to each of the numbers 16, 26 and 40 so that the resulting numbers may be in continued proportion?
Solution:
Let x be added to each number then
16 + x, 26 + x and 40 + x
are in continued proportion.

Question 11.
Find two numbers such that the mean proportional between them is 28 and the third proportional to them is 224.
Solution:
Let the two numbers are a and b.
∵ 28 is the mean proportional
∵ a : 28 : : 28 : b

Question 12.
If b is the mean proportional between a and c, prove that a, c, a² + b², and b² + c² are proportional.
Solution:
∵ b is the mean proportional between a and c, then,
b² = a × c ⇒ b² = ac …(i)

Question 13.
If b is the mean proportional between a and c, prove that (ab + bc) is the mean proportional between (a² + b²) and (b² + c²).
Solution:
b is the mean proportional between a and c then
b² = ac …(i)
Now if (ab + bc) is the mean proportional

Question 14.
If y is mean proportional between x and z, prove that
xyz (x + y + z)³ = (xy + yz + zx)³.
Solution:
∵ y is the mean proportional between
x and z, then
y² = xz …(i)

Question 15.
If a + c = mb and \(\frac { 1 }{ b } +\frac { 1 }{ d } =\frac { m }{ c } \), prove that a, b, c and d are in proportion.
Solution:
a + c = mb and \(\frac { 1 }{ b } +\frac { 1 }{ d } =\frac { m }{ c } \)
a + c = mb

Question 16.
If \(\frac { x }{ a } =\frac { y }{ b } =\frac { z }{ c } \), prove that
(i)\(\frac { { x }^{ 3 } }{ { a }^{ 2 } } +\frac { { y }^{ 3 } }{ { b }^{ 2 } } +\frac { { z }^{ 3 } }{ { c }^{ 2 } } =\frac { { \left( x+y+z \right) }^{ 3 } }{ { \left( a+b+c \right) }^{ 2 } } \)

Solution:
\(\frac { x }{ a } =\frac { y }{ b } =\frac { z }{ c } \)
∴ x = ak, y = bk, z = ck

Question 17.
If \(\frac { a }{ b } =\frac { c }{ d } =\frac { e }{ f } \) prove that :
(i) (b² + d² + f²) (a² + c² + e²) = (ab + cd + ef)²

Solution:
\(\frac { a }{ b } =\frac { c }{ d } =\frac { e }{ f } \) = k(say)
∴ a = bk, c = dk, e =fk

Question 18.
If ax = by = cz; prove that
\(\frac { { x }^{ 2 } }{ yz } +\frac { { y }^{ 2 } }{ zx } +\frac { { z }^{ 2 } }{ xy } \) = \(\frac { bc }{ { a }^{ 2 } } +\frac { ca }{ { b }^{ 2 } } +\frac { ab }{ { c }^{ 2 } } \)
Solution:
Let ax = by = cz = k

Question 19.
If a, b, c and d are in proportion, prove that:
(i) (5a + 7b) (2c – 3d) = (5c + 7d) (2a – 3b)
(ii) (ma + nb) : b = (mc + nd) : d
(iii) (a⁴ + c⁴) : (b⁴ + d⁴) = a² c² : b² d².

Solution:
∵ a, b, c, d are in proportion
\(\\ \frac { a }{ b } \) = \(\\ \frac { c }{ d } \) = k(say)

Question 20.
If x, y, z are in continued proportion, prove that:\(\frac { { \left( x+y \right) }^{ 2 } }{ { \left( y+z \right) }^{ 2 } } =\frac { x }{ z } \). (2010)
Solution:
x, y, z are in continued proportion
Let \(\\ \frac { x }{ y } \) = \(\\ \frac { y }{ z } \) = k

Question 21.
If a, b, c are in continued proportion, prove that:
\(\frac { { pa }^{ 2 }+qab+{ rb }^{ 2 } }{ { pb }^{ 2 }+qbc+{ rc }^{ 2 } } =\frac { a }{ c } \)
Solution:
Given a, b, c are in continued proportion
\(\frac { { pa }^{ 2 }+qab+{ rb }^{ 2 } }{ { pb }^{ 2 }+qbc+{ rc }^{ 2 } } =\frac { a }{ c } \)
Let \(\\ \frac { a }{ b } \) = \(\\ \frac { b }{ c } \) = k

Question 22.
If a, b, c are in continued proportion, prove that:
(i) \(\frac { a+b }{ b+c } =\frac { { a }^{ 2 }(b-c) }{ { b }^{ 2 }(a-b) } \)

Solution:
As a, b, c, are in continued proportion
Let \(\\ \frac { a }{ b } \) = \(\\ \frac { b }{ c } \) = k

Question 23.
If a, b, c, d are in continued proportion, prove that:
(i) \(\frac { { a }^{ 3 }+{ b }^{ 3 }+{ c }^{ 3 } }{ { b }^{ 3 }+{ c }^{ 3 }+{ d }^{ 3 } } =\frac { a }{ d } \)

Solution:
a, b, c, d are in continued proportion
∴ \(\frac { a }{ b } =\frac { b }{ c } =\frac { c }{ d } =k(say)\)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Chapter Test

Question 1.
(i)\(\begin{bmatrix} 2 & -1 \\ 5 & 1 \end{bmatrix}\)
(ii)[2 3 – 7]
(iii)\(\left[ \begin{matrix} 3 \\ 0 \\ -1 \end{matrix} \right] \)
(iv)\(\left[ \begin{matrix} \begin{matrix} 2 \\ 0 \\ 1 \end{matrix} & \begin{matrix} -4 \\ 0 \\ 7 \end{matrix} \end{matrix} \right] \)
(v)\(\left[ \begin{matrix} \begin{matrix} 2 & 7 & 8 \end{matrix} \\ \begin{matrix} -1 & \sqrt { 2 } & 0 \end{matrix} \end{matrix} \right] \)
(vi)\(\left[ \begin{matrix} \begin{matrix} 0 & 0 & 0 \end{matrix} \\ \begin{matrix} 0 & 0 & 0 \end{matrix} \end{matrix} \right] \)
Solution:
(i) It is square matrix of order 2
(ii) It is row matrix of order 1 × 3
(iii) It is column matrix of order 3 × 1
(iv) It is matrix of order 3 × 2
(v) It is matrix of order 2 × 3
(vi) It is zero matrix of order 2 × 3

Question 2.
(i) If a matrix has 4 elements, what are the possible order it can have ?
(ii) If a matrix has 8 elements, what are the possible order it can have ?
Solution:
(i) It can have 1 × 4, 4 × 1 or 2 × 2 order
(ii) It can have 1 × 8, 8 × 1,2 × 4 or 4 × 2 order

Question 3.
Construct a 2 x 2 matrix whose elements a_ij are given by
(i) a_ij = 2i – j
(ii) a_ij = i.j
Solution:
(i) It can be \(\begin{bmatrix} 1 & 0 \\ 3 & 2 \end{bmatrix}\)
(ii) It can be \(\begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}\)

Question 4.
Find the values of x and y if : \(\left[ \begin{matrix} 2x+y \\ 3x-2y \end{matrix} \right] =\left[ \begin{matrix} 5 \\ 4 \end{matrix} \right] \)
Solution:
Comparing corresponding elements,
2x + y = 5 …(i)
3x – 2y = 4 …(ii)
Multiply (i) by 2 and (ii) by ‘1’ we get
4x + 2y = 10, 3x – 2y = 4
Adding we get, 7x = 14 ⇒ x = 2
Substituting the value of x in (i)
2 x 2 + y = 5 ⇒ 4 + y = 5
y = 5 – 4 = 1
Hence x = 2, y = 1

Question 5.
Find the value of x if \(\left[ \begin{matrix} \begin{matrix} 3x+y & \quad -y \end{matrix} \\ \begin{matrix} 2y-x & \quad \quad 3 \end{matrix} \end{matrix} \right] =\begin{bmatrix} 1 & 2 \\ -5 & 3 \end{bmatrix} \)
Solution:
\(\left[ \begin{matrix} \begin{matrix} 3x+y & \quad -y \end{matrix} \\ \begin{matrix} 2y-x & \quad \quad 3 \end{matrix} \end{matrix} \right] =\begin{bmatrix} 1 & 2 \\ -5 & 3 \end{bmatrix} \)
Comparing the corresponding terms, we get.
-y = 2
⇒ y = -2

Question 6.
If \(\left[ \begin{matrix} \begin{matrix} x+3 & \quad \quad 4 \end{matrix} \\ \begin{matrix} y-4 & \quad \quad x+y \end{matrix} \end{matrix} \right] =\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \) ,find values of x and y
Solution:
\(\left[ \begin{matrix} \begin{matrix} x+3 & \quad \quad 4 \end{matrix} \\ \begin{matrix} y-4 & \quad \quad x+y \end{matrix} \end{matrix} \right] =\begin{bmatrix} 5 & 4 \\ 3 & 9 \end{bmatrix} \)
Comparing the corresponding terms, we get.
x + 3 = 5
⇒ x = 5 – 3 = 2
⇒ y – 4 = 3
⇒ y = 3 + 4 = 7
x = 2, y = 7

Question 7.
Find the values of x, y and z if
\(\left[ \begin{matrix} \begin{matrix} x+2 & \quad \quad 6 \end{matrix} \\ \begin{matrix} 3 & \quad \quad \quad 5z \end{matrix} \end{matrix} \right] =\begin{bmatrix} -5 & \quad { y }^{ 2 }+y \\ 3 & -20 \end{bmatrix}\)
Solution:
Comparing the corresponding elements of equal determinents,
x + 2 = -5
⇒ x = -5 – 2 = -7

Question 8.
Find the values of x, y, a and b if
\(\begin{bmatrix} x-2 & y \\ a+2b & 3a-b \end{bmatrix}=\begin{bmatrix} 3 & 1 \\ 5 & 1 \end{bmatrix}\)
Solution:
Comparing corresponding elements
x – 2 = 3, y = 1
x = 3 + 2 = 5
a + 2b = 5 ……(i)
3a – b = 1 ……..(ii)

Question 9.
Find the values of a, b, c and d if
\(\begin{bmatrix} a+b & 3 \\ 5+c & ab \end{bmatrix}=\begin{bmatrix} 6 & d \\ -1 & 8 \end{bmatrix} \)
Solution:
\(\begin{bmatrix} a+b & 3 \\ 5+c & ab \end{bmatrix}=\begin{bmatrix} 6 & d \\ -1 & 8 \end{bmatrix} \)
Comparing the corresponding terms, we get.
3 = d ⇒ d = 3
⇒ 5 + c = – 1
⇒ c = -1 – 5
⇒ c = -6
a + b = 6 and ab = 8

Question 10.
Find the values of x, y, a and b, if
\(\left[ \begin{matrix} \begin{matrix} 3x+4y & 2 & x-2y \end{matrix} \\ \begin{matrix} a+b & 2a-b & -1 \end{matrix} \end{matrix} \right] =\left[ \begin{matrix} \begin{matrix} 2 & \quad 2\quad & 4 \end{matrix} \\ \begin{matrix} 5 & -5 & -1 \end{matrix} \end{matrix} \right] \)
Solution:
Comparing the corresponding terms, we get.
3x + 4y = 2 ……(i)
x – 2y = 4 …….(ii)
Multiplying (i) by 1 and (ii) by 2

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 8 Matrices Ex 8.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test

Question 1.
(i) Find two consecutive natural numbers such that the sum of their squares is 61.
(ii) Find two consecutive integers such that the sum of their squares is 61.
Solution:
Let the first natural number = x
then second natural number = x + 1
According to the condition, (x)² + (x + 1)² = 61

Question 2.
(i) If the product of two positive consecutive even integers is 288, find the integers.
(ii) If the product of two consecutive even integers is 224, find the integers.
(iii) Find two consecutive even natural numbers such that the sum of their squares is 340.
(iv) Find two consecutive odd integers such that the sum of their squares is 394.
Solution:
(i) Let first positive even integer = 2x
then second even integer = 2x + 2
According to the condition,
2x × (2x + 2) = 288
⇒ 4x² + 4x – 288 = 0
⇒ x² + x – 72 = 0 (Dividing by 4)

Question 3.
The sum of two numbers is 9 and the sum of their squares is 41. Taking one number as x, form ail equation in x and solve it to find the numbers.
Solution:
Sum of two numbers = 9
Let first number = x
then second number = 9 – x
Now according to the condition,

Question 4.
Five times a certain whole number is equal to three less than twice the square of the number. Find the number.
Solution:
Let number = x
Now according to the condition,
5x = 2x² – 3

Question 5.
Sum of two natural numbers is 8 and the difference of their reciprocal is 2/15. Find the numbers.
Solution:
Let x and y be two numbers
Given that, x + y = 8 ……(i)

Question 6.
The difference between the squares of two numbers is 45. The square of the smaller number is 4 times the larger number. Determine the numbers.
Solution:
Let the larger number = x
then smaller number = y
Now according to the condition,

Question 7.
There are three consecutive positive integers such that the sum of the square of the first and the product of other two is 154. What are the integers?
Solution:
Let the first integer = x
then second integer = x + 1
and third integer = x + 2
Now according to the condition,

Question 8.
(i) Find three successive even natural numbers, the sum of whose squares is 308.
(ii) Find three consecutive odd integers, the sum of whose squares is 83.
Solution:
(i) Let first even number = 2x
second even number = 2x + 2
third even number = 2x + 4
Now according to the condition,

Question 9.
In a certain positive fraction, the denominator is greater than the numerator by 3. If 1 is subtracted from both the numerator and denominator, the fraction is decreased by \(\\ \frac { 1 }{ 14 } \). Find the fraction.
Solution:
Let the numerator of a fraction = x
then denominator = x + 3
then fraction = \(\\ \frac { x }{ x+3 } \)
Now according to the condition,

Question 10.
The sum of the numerator and denominator of a certain positive fraction is 8. If 2 is added to both the numerator and denominator, the fraction is increased by \(\\ \frac { 4 }{ 35 } \). Find the fraction.
Solution:
Let the denominator of a positive fraction = x
then numerator = 8 – x

Question 11.
A two digit number contains the bigger at ten’s place. The product of the digits is 27 and the difference between two digits is 6. Find the number.
Solution:
Let unit’s digit = x
then tens digit = x + 6
Number = x + 10(x + 6)
= x + 10x + 60
= 11x + 60

Question 12.
A two digit positive number is such that the product of its digits is 6. If 9 is added to the number, the digits interchange their places. Find the number. (2014)
Solution:
Let 2-digit number = xy = 10x + y
Reversed digits = yx = 10y + x
According to question,

Question 13.
A rectangle of area 105 cm² has its length equal to x cm. Write down its breadth in terms of x. Given that the perimeter is 44 cm, write down an equation in x and solve it to determine the dimensions of the rectangle.
Solution:
Perimeter of rectangle = 44 cm
length + breadth = \(\\ \frac { 44 }{ 2 } \) = 22 cm
Let length = x
then breadth = 22 – x
According to the condition,

Question 14.
A rectangular garden 10 m by 16 m is to be surrounded by a concrete walk of uniform width. Given that the area of the walk is 120 square metres, assuming the width of the walk to be x, form an equation in x and solve it to find the value of x. (1992)
Solution:
Length of garden = 16 m
and width = 10 m
Let the width of walk = x m
Outer length = 16 + 2x
and outer width = 10 + 2x
Now according to the condition,

Question 15.
(i) Harish made a rectangular garden, with its length 5 metres more than its width. The next year, he increased the length by 3 metres and decreased the width by 2 metres. If the area of the second garden was 119 sq m, was the second garden larger or smaller ?
(ii) The length of a rectangle exceeds its breadth by 5 m. If the breadth were doubled and the length reduced by 9 m, the area of the rectangle would have increased by 140 m². Find its dimensions.
Solution:
In first case,
Let length of the garden = x m
then width = (x – 5) m
Area = l x b = x(x – 5) sq. m
In second case,

Question 16.
The perimeter of a rectangular plot is 180 m and its area is 1800 m². Take the length of the plot as x m. Use the perimeter 180 m to write the value of the breadth in terms of x. Use the values of length, breadth and the area to write an equation in x. Solve the equation to calculate the length and breadth of the plot. (1993)
Solution:
The perimeter of a rectangular field = 180 m
and area = 1800 m²
Let length = x m

Question 17.
The lengths of the parallel sides of a trapezium are (x + 9) cm and (2x – 3) cm and the distance between them is (x + 4) cm. If its area is 540 cm², find x.
Solution:
Area of a trapezium = \(\\ \frac { 1 }{ 2 } \)
(sum of parallel sides) x height
Lengths of parallel sides are (x + 9) and (2x – 3)
and height = (x + 4)
According to the condition,

Question 18.
If the perimeter of a rectangular plot is 68 m and the length of its diagonal is 26 m, find its area.
Solution:
Perimeter = 68 m and diagonal = 26 m
Length + breadth = \(\\ \frac { 68 }{ 2 } \) = 34 m
Let length = x m
then breadth = (34 – x) m

Question 19.
If the sum of two smaller sides of a right – angled triangle is 17cm and the perimeter is 30cm, then find the area of the triangle.
Solution:
The perimeter of the triangle = 30 cm.
Let one of the two small sides = x
then, other side = 17 – x

Question 20.
The hypotenuse of grassy land in the shape of a right triangle is 1 metre more than twice the shortest side. If the third side is 7 metres more than the shortest side, find the sides of the grassy land.
Solution:
Let the shortest side = x
Hypotenuse = 2x + 1
and third side = x + 7
According to the condition,

Question 21.
Mohini wishes to fit three rods together in the shape of a right triangle. If the hypotenuse is 2 cm longer than the base and 4 cm longer than the shortest side, find the lengths of the rods.
Solution:
Let the length of hypotenuse = x cm
then base = (x – 2) cm
and shortest side = x – 4
According to the condition,

Question 22.
In a P.T. display, 480 students are arranged in rows and columns. If there are 4 more students in each row than the number of rows, find the number of students in each row.
Solution:
Total number of students = 480
Let the number of students in each row = x

Question 23.
In an auditorium, the number of rows are equal to the number of seats in each row.If the number of rows is doubled and number of seats in each row is reduced by 5, then the total number of seats is increased by 375. How many rows were there?
Solution:
Let the number of rows = x
then no. of seats in each row = x
and total number of seats = x × x = x²
According to the condition,

Question 24.
At an annual function of a school, each student gives the gift to every other student. If the number of gifts is 1980, find the number of students.
Solution:
Let the number of students = x
then the number of gifts given = x – 1
Total number of gifts = x (x – 1)
According to the condition,
x (x – 1) = 1980

Question 25.
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain, its speed gets reduced by 10 km/h and as such it takes two hours longer to cover the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate x. (2016)
Solution:
Distance = 240 km
Let speed of a bus = x km/hr

Question 26.
The speed of an express train is x km/hr and the speed of an ordinary train is 12 km/hr less than that of the express train. If the ordinary train takes one hour longer than the express train to cover a distance of 240 km, find the speed of the express train.
Solution:
Let the speed of express train = x km
Then speed of the ordinary train = (x – 12) km
Time is taken to cover 240 km by the express

Question 27.
A car covers a distance of 400 km at a certain speed. Had the speed been 12 km/h more, the time taken for the journey would have been 1 hour 40 minutes less. Find the original speed of the car. (1996)
Solution:
Let the original speed of the car = x km/h.
Distance covered = 400 km

Question 28.
An aeroplane travelled a distance of 400 km at an average speed of x km/hr. On the return journey, the speed was increased by 40 km/hr. Write down an expression for the time taken for
(i)the onward journey,
(ii) the return journey.
If the return journey took 30 minutes less than the onward journey, write down an equation in x and find its value. (2002)
Solution:
Distance = 400 km
Speed of aeroplane = x km/hr

Question 29.
The distance by road between two towns A and B, is 216 km, and by rail it is 208 km. A car travels at a speed of x km/hr, and the train travels at a speed which is 16 km/hr faster than the car. Calculate :
(i) The time taken by the car, to reach town B from A, in terms of x ;
(ii) The time taken by the train, to reach town B from A, in terms of x ;
(iii) If the train takes 2 hours less than the car, to reach town B, obtain an equation in x and solve it.
(iv) Hence find the speed of the train. (1998)
Solution:
The distance by road between A and B = 216 km
and the distance by rail = 208 km
speed of car = x km/hr

Question 30.
An aeroplane flying with a wind of 30 km/hr takes 40 minutes less to fly 3600 km, than what it would have taken to fly against the same wind. Find the planes speed of flying in still air.
Solution:
Let the speed of the plane in still air = x km/hr
Speed of wind = 30 km/hr
Distance = 3600 km

Question 31.
A school bus transported an excursion party to a picnic spot 150 km away. While returning, it was raining and the bus had to reduce its speed by 5 km/hr, and it took one hour longer to make the return trip. Find the time taken to return.
Solution:
Distance = 150 km
Let the speed of bus = x km/hr

Question 32.
A boat can cover 10 km up the stream and 5 km down the stream in 6 hours. If the speed of the stream is 1.5 km/hr. find the speed of the boat in still water.
Solution:
Distance up stream = 10 km
and down stream = 5 km
Total time is taken = 6 hours
Speed of stream = 1.5 km/hr
Let the speed of a boat in still water = x km/hr
According to the condition,

Question 33.
Two pipes running together can fill a tank in \({ 11 }^{ 1/9 }\) minutes. If one pipe takes 5 minutes more than the other to fill the tank, find the time in which each pipe would/fill the tank.
Solution:
Let the time taken by one pipe = x minutes
Then time taken by second pipe = (x + 5) minutes
Time taken by both pipes = \({ 11 }^{ 1/9 }\) minutes
Now according to the condition.

Question 34.
(i) Rs. 480 is divided equally among ‘x’ children. If the number of children was 20 more then each would have got Rs. 12 less. Find ‘x’.
(ii) Rs. 6500 is divided equally among a certain number of persons. Had there been 15 more persons, each would have got Rs. 30 less. Find the original number of persons.
Solution:
(i) Share of each child = Rs \(\\ \frac { 480 }{ x } \)
According to the question

Question 35.
2x articles cost Rs. (5x + 54) and (x + 2) similar articles cost Rs. (10x – 4), find x.
Solution:
Cost of 2x articles = 5x + 54
Cost of 1 article = \(\\ \frac { 5x+54 }{ 2x } \) ….(i)
Again cost of x + 2 articles = 10x – 4

Question 36.
A trader buys x articles for a total cost of Rs. 600.
(i) Write down the cost of one article in terms of x. If the cost per article were Rs. 5 more, the number of articles that can be bought for Rs. 600 would be four less.
(ii) Write down the equation in x for the above situation and solve it to find x. (1999)
Solution:
Total cost = Rs. 600,
No. of articles = x

Question 37.
A shopkeeper buys a certain number of books for Rs 960. If the cost per book was Rs 8 less, the number of books that could be bought for Rs 960 would be 4 more. Taking the original cost of each book to be Rs x, write an equation in x and solve it to find the original cost of each book.
Solution:
Let original cost = Rs x
No. of books bought = \(\\ \frac { 960 }{ x } \)
New cost of books = Rs (x – 8)

Question 38.
A piece of cloth costs Rs. 300. If the piece was 5 metres longer and each metre of cloth costs Rs. 2 less, the cost of the piece would have remained unchanged. How long is the original piece of cloth and what is the rate per metre?
Solution:
The total cost of cloth piece = Rs. 300
Let the length of the piece of cloth in the beginning = x m

Question 39.
The hotel bill for a number of people for an overnight stay is Rs. 4800. If there were 4 more, the bill each person had to pay would have reduced by Rs. 200. Find the number of people staying overnight. (2000)
Solution:
Let the number of people = x
Amount of bill = Rs. 4800

Question 40.
A person was given Rs. 3000 for a tour. If he extends his tour programme by 5 days, he must cut down his daily expenses by Rs. 20. Find the number of days of his tour programme.
Solution:
Let the number of days of tour programme = x
Amount = Rs. 3000

Question 41.
Ritu bought a saree for Rs. 60 x and sold it for Rs. (500 + 4x) at a loss of x%. Find the cost price.
Solution:
The cost price of saree = Rs. 60x
and selling price = Rs. (500 + 4x)
Loss = x%
Now according to the condition

Question 42.
(i) The sum of the ages of Vivek and his younger brother Amit is 47 years. The product of their ages in years is 550. Find their ages. (2017)
(ii) Paul is x years old and his father’s age is twice the square of Paul’s age. Ten years hence, the father’s age will be four times Paul’s age. Find their present ages.
Solution:
(i) Let Vivek’s present age be x years.
His brother’s age = (47 – x) years
According to question,
x(47 – x) = 550
⇒ 47x – x² = 550
⇒ x² – 47x + 550 = 0
⇒ x² – 25x – 22x + 550 = 0
⇒ x(x – 25) – 22(x – 25) – 0

Question 43.
The age of a man is twice the square of the age of his son. Eight years hence, the age of the man will be 4 years more than three times the age of his son. Find the present age.
Solution:
Let the present age of the son = x years
then, the present age of the man = 2x² years.
8 years hence,
The age of son will be = (x + 8) years and the
age of man = (2x² + 8) years
According to the problem,

Question 44.
Two years ago, a man’s age was three times the square of his daughter’s age. Three years hence, his age will be four times his daughter’s age. Find their present ages.
Solution:
2 years ago,
Let the age of daughter = x
age of man = 3x²
then present age of daughter = x + 2
and mean = 3x² + 2

Question 45.
The length (in cm) of the hypotenuse of a right-angled triangle exceeds the length of one side by 2 cm and exceeds twice the length of another side by 1 cm. Find the length of each side. Also, find the perimeter and the area of the triangle.
Solution:
Let the length of one side = x cm
and other side = y cm.
then hypotenues = x + 2, and 2y + 1

Question 46.
If twice the area of a smaller square is subtracted from the area of a larger square, the result is 14 cm². However, if twice the area of the larger square is added to three times the area of the smaller square, the result is 203 cm². Determine the sides of the two squares.
Solution:
Let the side of smaller square = x cm
and side of bigger square = y cm
According to the condition,

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.