Circuit Diagram
A circuit diagram is a schematics diagram of an electric circuit in which different components of the circuit are represented by conventionally used symbols.
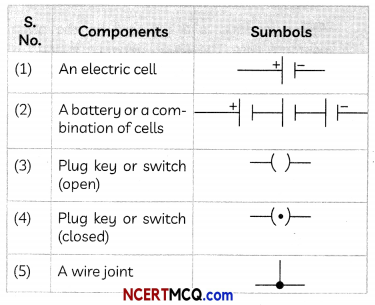
A circuit diagram is a schematics diagram of an electric circuit in which different components of the circuit are represented by conventionally used symbols.


The electric potential at a point is defined as the work done in moving a unit positive charge from infinity to that point.
Potential Difference between two points on a conductor carrying current is defined as the work defined in moving a unit positive charge from one point to the other.
Potential Difference = \(\frac{\text { Work Done }(\mathrm{W})}{\text { Charge }(\mathrm{Q})}\)
Example 1.
How much energy is given to each coulomb of charge passing through a 6 V battery?
Answer:
It is given that charge q = 1 C, V = 6V.
We know that work done W = q V = 1 × 6J = 6J.
Therefore, 6J energy is given to one coulomb of charge passing through a 6 V battery.
![]()
Volt: One volt is the potential difference be¬tween two points in a current-carrying conduc¬tor when 1 Joule of work is done in moving a charge of 1 Coulomb from one point to another.
1 Volt = \(\frac{1 \text { Joule }}{1 \text { Coulomb }}\)
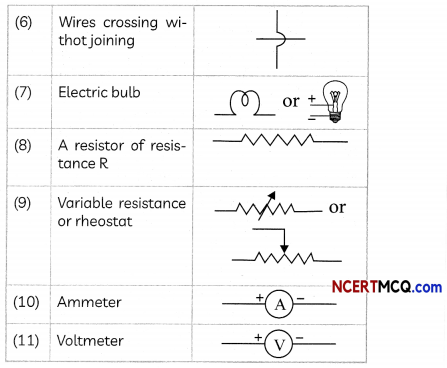
Voltmeter: It is an instrument to measure the potential difference. The voltmeter is always connected in parallel across the points between which the potential difference is to be measured.
Electricity is a form of energy and can be readily transmitted over large distances with relatively small loss in energy. In this chapter we will discuss about electric circuits, potential difference and flow of current in an electric circuit. We will also discuss Ohm’s law and the heating effect of electric current and its applications.
A continuous and closed path of an electric current is called an electric circuit.
Electric current is expressed by the amount of charge flowing through a particular of area in unit time. It is defined as the rate of flow electric charges i.e., the charge flowing per unit time.
Let Q denote the amount of charge flowing across a given point in the conductor in time t, then the current flowing is given by, I = Q/t.
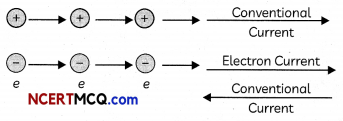
It is the direction in which the positive charges flow which is opposite to the direction of the flow of negative charges.
Ampere: One Ampere is defined as the current flowing when 1 Coulomb of charge flows across a point in 1 second.
1 Ampere = \(\frac{1 \text { Coulomb }}{1 \text { second }}\)
Small quantities of current are expressed in milliampere (1 mA = 10-3 A) or in microampere (1 yA = 10-6A).
Coulomb: It is the SI unit of charge and is the charge carried by 6 × 1018 electrons, since the charge of 1 electron = 1.6 × 10-19 C.
![]()
Example 1.
Calculate the number of electrons constituting one coulomb of charge.
Answer:
The charge on one electron (e) = 1.6 × 10-19 C.
Also, Charge q = ne, where n is the number of electrons. Therefore,
n = \(\frac{q}{e}=\frac{1}{1.6 \times 10^{-19}}\) = 6.25 × 1018 electrons
e 1.6 × 10-19
Ammeter: It is an instrument to measure electric current in a circuit and is always connected in series in a circuit through which the current is to be measured. The electric current flows in the circuit shown from the positive terminal to the negative terminal of the cell through the bulb and the ammeter.
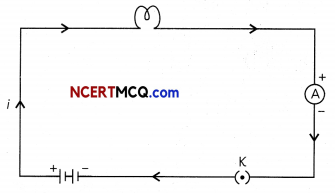
Figure above shows the schematic diagram of a typical electric circuit comprising a celL, an electric bulb, an ammeter and a plug key. The electric current flows in the circuit from the positive terminal of the cell to the negative terminal of the cell through the bulb and ammeter.
The flow of charge inside a conductor: When a wire is connected to a battery, the electrons which were drifting randomly in all directions, now become aligned in a particular direction and current begins to flow across the wire. When a steady current flows through a conductor, the electrons in it move with a certain average drift velocity.
The phenomenon of change in the direction of light on striking an obstacle like an atom, a molecule, dust particle, water droplet etc is known as scattering of Light. It involves bouncing off electromagnetic radiation by atoms/molecules of the medium through which they are travelling.
Tyndall effect deals with the phenomenon of scattering of light by colloidal particles.
The colour of the scattered light depends on the size of the scattering particle. Very fine particles scatter mainly blue light while particles of Larger size scatter light of Longer wavelength. If the size of the scattering particle is large enough, then the scattered light may even appear white.
![]()
The blue colour of the sky is due to the scattering of light by the large numbers of molecules present in the earth’s atmosphere. As the size of the scatterer is much smaller than the wavelength of light, light of a smaller wavelength is scattered the most. If the earth had no atmosphere, the sky would appear black in the day time as no colour of sunlight would be scattered then.
Clouds are visible to us due to scattering of light from lower parts of earth’s atmosphere which contains dust particles, water droplets, ice particles etc. As the size of the scatterer is much larger than the wavelength, all wavelengths are scattered nearly equally, due to which clouds appear generally white.
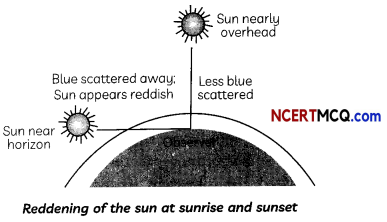
At the time of sunrise and sunset, the sun is near the horizon due to which sunrays have to travel much larger part of the atmosphere. Most of the blue light is thus scattered away. The red colour having the longest wavelength is scattered the least and hence enters our eyes. When the sun is nearly overhead, the sunlight has to pass through much smaller portion of earth’s atmosphere due to which scattering is much less and the sun looks white.
Atmospheric refraction is the refraction of light by the earth’s atmosphere due to the decrease of refractive index with decreasing density or increasing temperature of air.
The stars appear slightly higher than its actual position when viewed near the horizon due to the phenomenon of atmospheric refraction. When the starlight enters the earth’s atmosphere, where its refractive index is increasing gradually, the starlight is bent towards the normal.
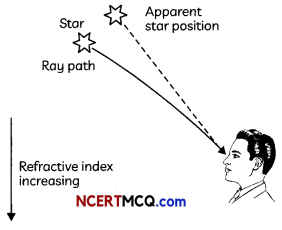
The apparent position of the star is not stationary, but keeps on changing slightly, since the physical conditions of the earth’s atmosphere are not stationary. Since the stars are very distant, they approximate point-sized sources of tight. As the path of rays of Light coming from the star goes on varying slightly, the apparent position of the star fluctuates and the amount of starlight entering the eye flickers – the star sometimes appears brighter, and at some other time, fainter, which is the twinkling effect.
![]()
Planets are much closer to the earth and therefore act as extended sources. A planet can therefore be considered as a collection of large number of point-sized objects such that the total variation in the amount of light entering our eye from all the individual point-sized sources will average to zero, and hence the twinkling effect is nullified.
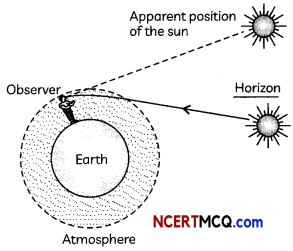
Advance sunrise and delayed sunset: The sun is visible to us 2 minutes before actual sunrise and 2 minutes after actual sunset due to atmospheric refraction.
The time difference between actual sunset and the apparent sunset is about 2 minutes. The apparent flattening of the Sun’s disc at sunrise and sunset is also due to the same phenomenon.
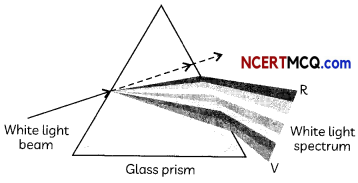
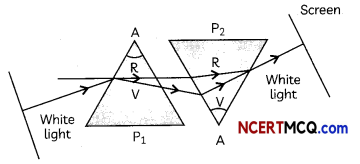
When white light is incident on a glass prism, it splits into a band of colours as the refracting surfaces of the glass prism are inclined at an angle.
Example 1.
Case Based:
Take a thick sheet of cardboard and make a smalt hole or narrow slit in its middle. Allow sunlight to fall on the narrow slit. This gives a narrow beam of white light. Now, take a glass prism and allow the light from the slit to fall on one of its faces as shown in figure.
Turn the prism slowly until the light that comes out of it appears on a nearby screen.
(A) When the prism is turned slowly in the above activity, it is observed that:
(I) White light comes out of the prism on a nearby screen
(II) A band of seven colours is observed on a nearby screen with red and Indigo colours at the two ends.
(III) A band of seven colours is observed on a nearby screen with Yellow and Violet colours at the two ends.
(IV) A band of seven colours is observed on a nearby screen with red and Violet colours at the two ends.
Select the incorrect observations from the above:
(a) Both (I) and (II)
(b) Both (II) and (III)
(c) (I), (II) and (III)
(d) (I), (III) and (IV)
Answer:
(c) (I), (II) and (III)
Explanation: When the prism is turned slowly, a band of seven colours is observed on a nearby screen, with red and violet colours at the two ends of the band. The various colours seen are Violet, Indigo, Blue, Green, Yellow, Orange and Red, as shown in figure. The band of the coloured components of a light beam is called its spectrum.
(B) The colour of light that has the minimum ve¬locity in the glass prism is:
(a) Red
(b) Green
(c) Blue
(d) Violet
Answer:
(d) Violet
Explanation: Violet colour has the minimum wavelength among the visible colours of the spectrum and deviates the maximum. This is because it has the minimum velocity in the glass prism since refractive index of glass is maximum for violet.
![]()
(C) Which colour of light deviates the most on passing white light through a prism?
Answer:
Violet colour deviates the most when white light is passed through a glass prism. This is be-cause violet has the least wavelength among the seven visible colours of spectrum and re-fractive index of glass for violet light is the maximum.
(D) When white light enters a glass prism from air, for which colour is the angle of deviation the least?
Answer:
The angle of deviation will be least for red colour as red colour has the longest wavelength among the visible colours of the spectrum and therefore refractive index of glass for red colour will be minimum. So, red will suffer the minimum deviation.
(E) Assertion (A): The rays of different colours emerge along different paths from a glass prism.
Reason (R): Light rays undergo refraction and bend away from the nor¬mal when they travel from glass prism to air.
(a) Both (A) and (R) are true and (R) is the correct explanation of the assertion.
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the assertion.
(c) (A) is true, but (R) is false.
(d) (A) is false, but (R) is true.
Answer:
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the (A).
Explanation: The rays of different colours emerge along different paths from a glass slab as the refractive index of glass is different for different colours due to which different colours bend by different amounts on passing through the glass prism. The reason given, though correct, does not explain the splitting of light into its constituent colours.
![]()
The splitting of light into its component colours is called dispersion of light.
The band of the coloured components of a light beam is known as its spectrum.The sequence of colours is Violet, Indigo, Blue, Green, Yellow, Orange and Red and is given by the famous acronym – VIBGYOR
Dispersion occurs because light rays of different colours travel with different speeds in a refractive medium. The refractive index of glass is largest for violet colour and least for red colour due to which violet colour is dispersed the maximum and red colour the least.
If a second identical prism is placed in an inverted position with respect to the first prism such that all colours of the spectrum pass through the second prism, then a beam of white light emerges from the other side of the second prism.
This observation gave Newton the idea that the sunlight is made up of seven colours.
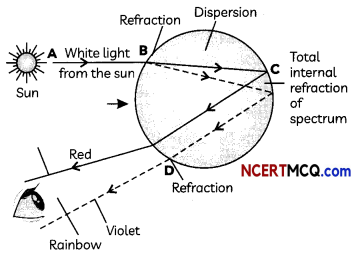
A rainbow is formed in the sky after a rain shower due to the dispersion of sunlight by the tiny droplets of water present in the atmosphere. It is always formed in a direction opposite to that of the Sun. The tiny droplets of water act like small prisms which refract and disperse the incident sunlight, then reflect the light internally and finally refract it again when it comes out of the raindrop. Different colours reach the observers eyes due to the dispersion of light and internal reflection.
Sometimes, the eye may gradually lose its power of accommodation due to which the person cannot see the objects distinctly and comfortably. The defects of vision are described below:
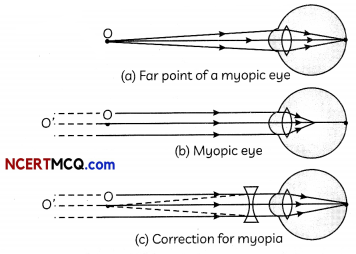
Myopia is also known as near-sightedness. A person can see nearby objects clearly but cannot see distant objects clearly as the image of the object is formed in front of the retina.
Causes of Myopia
Correction of Myopia
Myopia be corrected by using a concave (diverging) lens of appropriate focal Iength (or Power):
![]()
Example 1.
The far point of a myopic person is 80 cm in front of the eye. What is the nature and power of the lens required to correct the problem?
Answer:
To find the nature and power of lens, we will use u = ∞, v = -80 cm.
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}=-\frac{1}{80}\) ⇒ f = – 80cm = – 0.8m
It is a concave lens of focal length 0.8 m. Power of lens = -1.25 D.
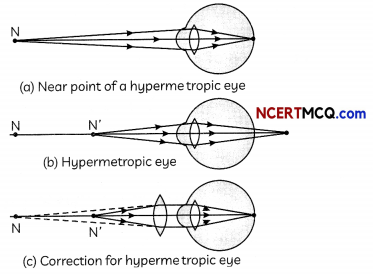
Hypermetropia can be corrected by using a convex (converging) lens of appropriate focal length (or Power).
Example 2.
A person needs a lens of power -5.5 dioptres for correcting his distant vision. For correcting his near vision he needs a Lens of power +1.5 dioptre. What is the focal length of the lens required for correcting (A) distant vision, and (B) near vision?
Answer:
The relation between power (P) and focal
(fin metres) is given by P = \(\frac{1}{f(\text { in } m)}\) length
(A) To find the focal length of the lens required for correcting distant vision, it is given that P = -5.5 D.
Therefore, using the reLation
P = \(\frac{1}{f(\text { in } m)}\)
⇒ f(in m) = \(\frac{1}{P}=+\frac{1}{5.5}\)
= + 0.67 m = + 66.67 cm
It is a concave lens of focal length 18 cm.
(B) To find the focal length of the lens required for correcting near vision, it is given that P = + 1.5 D.
Therefore, using the relation
P = \(\frac{1}{f(\text { in } m)}\)
⇒ f (in m)
= + 0.67 m = + 66.67 cm
It is a convex Lens of focal Length 66.67 cm.
With ageing, the near point of most people gradually recedes due to which they are unable to see nearby objects distinctly. A person may suffer from both myopia and hypermetropia
Causes of Presbyopia
Correction of Presbyopia
For a person suffering from both myopia and hypermetropia, bi-focal lenses are required in which the upper part is a concave lens and lower part is a convex lens.
![]()
Example 3.
The human eye can focus objects at different distances by adjusting the focal length of the eye lens. This is due to
(a) presbyopia.
(b) accommodation.
(c) near-sightedness.
(d) far-sightedness.
Answer:
(b) accommodation.
Explanation: The ability of the human eye to focus on nearby and distant objects by changing the curvature and hence focal length of the eye lens is called accommodation of the eye.
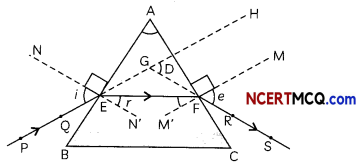
A prism has two triangular bases and three rectangular lateral surfaces which are inclined to each other. The angle between its two lateral faces is called the angle of the prism. In the figure,
PE – Incident ray ∠i – Angle of incidence
EF – Refracted ray ∠r – Angle of refraction
FS – Emergent ray ∠e – Angle of emergence
∠A – Angle of the prism ∠D – Angle of deviation
Optical instruments, including our eyes, extend the range of our vision and enable us to see objects varying in size from very tiny, nearby objects to very large, distant objects, in this chapter we shall study about the human eye and optical phenomena in nature, such as rainbow formation, splitting of white light and blue colour of the sky, etc.
The human eye is one of the most wonderful sense organs as it enables us to see various things and colours around us. It is like a camera.
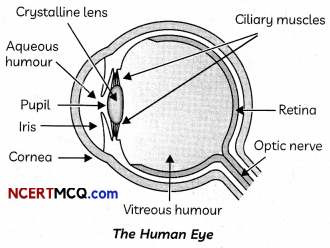
Retina:
This is a light sensitive screen inside the eye on which an inverted and real image of an object is formed by the eye lens. It contains light sensitive cells called rods and cones.
Cornea:
Cornea is a thin membrane covering the transparent bulge on the surface of the eyeball and through which light enters the eyes.
Aqueous Humour:
Aqueous humour acts as a lens along with the cornea and provides most of the refraction of light rays entering the eyes.
Crystalline Lens:
Crystalline lens provides the finer adjustment of focal length required to focus objects lying at various distances on the retina. It is composed of a fibrous jelly-like substance.
Iris:
Iris is a dark muscular assembly which lies behind the cornea and controls the size of the pupil.
Pupil:
Pupil is a variable aperture which regulates the amount of light entering the eyes. When the light is very bright, the pupil becomes very small (as the iris muscles contract) and in dim light, it opens up (as the iris muscles relax).
![]()
The ciliary muscles change the shape or curvature of the eye lens so that nearby, as well as distant objects, can be focused. The ciliary muscles contract when we are looking at nearby objects so that the eye lens becomes more round in shape thus reducing the focal length of the lens. When looking at distant objects, the eye lens relaxes, so that these objects can be seen clearly. The focal length of the eye lens is about 2.5 cm when the muscles are relaxed.
If due to damage or malfunction of any part of the visual system, there is a significant loss of visual functioning, it is called visual impairment. It can be due to damage to any of the structures involved in the transmission of light such as cornea, pupil, eye lens, etc or those responsible for the conversion of light to electrical impulses, like the retina or optic nerve.
Power of Accommodation is the ability of the eye lens to focus at nearby as well as distant objects by adjusting its focal length. For viewing nearby objects, the eye Lens becomes thick and for viewing distant objects, the eye lens becomes thin.
Least distance of distinct vision or near point: It is the minimum distance at which objects can be seen most distinctly without strain and is 25 cm for a normal eye.
Far point: It is the farthest point upto which the eye can see objects clearly and is infinity for a normal eye.
Power of accommodation: It is the maximum varia¬tion of the power of the eye for focusing on near and distant objects and is about 4 dioptres for a young adult with normal vision.
Cataract: It occurs when the crystalline lens of our eyes becomes hazy or even opaque due to the de-velopment of a membrane over it. It usually occurs at old age and leads to the decrease or loss of vision, but can be corrected by surgery.
Reason for having two eyes: Plaving two eyes gives us a wider field of view of about 180° with two eyes as compared to 150 with one eye. It also enables us to detect faint objects. Our eyes are positioned on the front of our heads which reduces the field of view in favour of stereopsis.
![]()
Example 1.
Why is a normal eye not able to see clearly the objects placed closer than 25 cm?
Answer:
A normal eye is not able to see clearly the objects placed closer than 25 cm as there is a limit to which the ciliary muscles can change the curvature of the eye lens. If the object is held closer than 25 cm, there is a lot of strain on the eyes.
When light travels from one medium to another, there is a change in its direction due to a change in speed of light. Consider a pencil that is partly immersed in water. The light reaching us from the portion of the pencil inside water seems to come from a different direction, compared to the part above water due to which the pencil appears to be displaced at the interface.
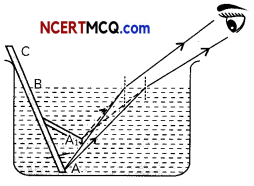
Example 1.
Case Based:
First, place a coin at the bottom of a bucket filled with water. With your eye to a side above water, try to pick up the coin in one go. Repeat the Activity.
Next, place a large shallow bowl on a table and put a coin in it. Move away slowly from the bowl. Stop when the coin just disappears from your sight. Ask a friend to pour water gently into the bowl without disturbing the coin. Keep looking for the coin from your position.
(A) Refer to the first activity. When a coin is placed at the bottom of a bucket filled with water and we try to pick up the coin with our eye to a side above the water:
(a) We are able to pick up the coin in one go
(b) We are able to pick up the coin but the coin slips from our hands as it is wet
(c) We are unable to pick up the coin as the water is too deep
(d) We are unable to pick up the coin in one go as the coin appears to be raised when kept in water.
Answer:
(d) We are unable to pick up the coin in one go as the coin appears to be raised when kept in water.
Explanation: The coin placed in water in a bucket appears to be raised as light rays travel from an optically denser medium (water) to an optically rarer medium (air) and hence bend away from the normal when they reach our eyes. The coin therefore appears to be raised.
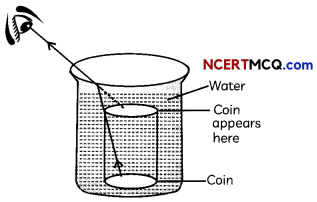
(B) In the second activity, the coin placed in a shallow bowl disappears when we move away from the bowl. When water is poured gently into the bowl:
(a) The coin will still not be visible
(b) The coin becomes visible again
(c) The coin appears to be at the bottom of the bowl
(d) The coin appears to be on the water surface.
Answer:
(b) The coin becomes visible again
Explanation: When water is gently poured into the bowl, the coin becomes visible again because due to refraction of Light travelling from water to air, the submerged coin seems raised to be above its actual level and thus becomes visible on seeing from the same side and distance. The coin appears slightly raised above its actual position due to refraction of light.
![]()
(C) What will be the absolute refractive index of a medium in which speed of light is 1.8 × 108 m/s?
Answer:
The absolute refractive index of a medium in which speed of light is 1.8 × 108 m/s will be 1.67.
Explanation: The absolute refractive index of a medium is defined as the ratio of speed of light in air or vacuum to the speed of light in the medium.
na = \(\frac{c}{v_{a}}=\frac{3 \times 10^{8}}{1.8 \times 10^{8}}=\frac{3}{1.8}\) = 1.67
(D) In which direction will light bend when it travels from a medium having refractive index 2.3 to a medium having refractive index 1.8?
Answer:
Light will bend away from the normal when it travels from the medium having refractive index 2.3 towards the medium having refractive index 1.8.
Explanation: A medium having refractive index 2.3 is optically more denser as compared to a medium having a refractive index 1.8. Therefore, light will bend away from the normal when it travels from the medium having refractive index 2.3 towards the medium having refractive index 1.8.
(E) Assertion (A): A coin kept in a shallow bowl appears to be raised.
Reason (R): Light rays undergo refraction and bend away from the normal when they travel from water to air.
(a) Both (A) and (R) are true and (R) is the correct explanation of the (A).
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the (A).
(c) (A) is true, but (R) is false.
(d) (A) is false, but(R) is true.
Answer:
(d) (A) is false, but (R) is true.
Explanation: When a coin is kept in a shallow bowl, there is no change in its apparent position as no refraction of light takes place. However, when it is kept in water, light undergoes refraction as it travels from water, which is an optically denser medium, to air, an optically rarer medium. Light rays bend away from the normal and hence the coin appears to be raised when kept in water.
The following are the laws of refraction:
The Refractive index
The refractive index of medium 2 with respect to medium 1 is defined as the ratio of the speed of light in first medium (v1) to the speed of light in the second medium (v2). It is linked to the relative speed of propagation of light in different media.
n21 = \(\frac{\text { Speed of light in first medium }\left(\mathrm{v}_{1}\right)}{\text { Speed of light in second medium }\left(\mathrm{v}_{2}\right)}\)
The refractive index of a medium with respect to vac-uum is called the absolute refractive index (the first medium is free space or vacuum). The refractive index of water is 1.33, which means that the ratio of speed of light in air and the speed of light in water is 1.33.
n = \(\frac{\text { Speed of light in vacuum (c) }}{\text { Speed of light in the medium (v’) }}\)
An optically denser medium may not possess greater mass density.
![]()
If n1 and n2 are the refractive indices of the first and the second medium with respect to vacuum, and the speed of light in the first and second medium is v1 and v2 respectively, Snell’s law can be written as,
n21 = \(\frac{\sin i}{\sin r}=\frac{v_{1}}{v_{2}}=\frac{\left(c / n_{1}\right)}{\left(c / n_{2}\right)}=\frac{n_{2}}{n_{1}}\)
A medium that has a larger refractive index as compared to another medium is called an optically denser medium. A ray of light travelling from a rarer medium to a denser medium bends towards the normal.
A medium that has a lower refractive index as compared to another medium is called an optically rarer medium. The speed of light is higher in a rarer medium than in a denser medium. Thus a ray of light travelling from a rare medium to a denser medium slows down and bends towards the normal.
Example 2.
The refractive index of diamond is 2.42. What is the meaning of this statement?
Answer:
The refractive index of diamond = 2.42 means
that 2.42 = \(\frac{c}{v}=\frac{3 \times 10^{8}}{v} \Rightarrow v=\frac{3 \times 10^{8}}{2.42}\)
where v = speed of light in diamond.
So, the statement means that the speed of light in diamond is less than the speed of light in vacuum by a factor of 2.42.
When a ray of light is incident from air (rarer medium) on a glass slab (denser medium), it bends towards the normal and when it emerges from the glass slab, the. emergent ray is parallel to the incident ray but is laterally displaced. The lateral displacement is proportional to the thickness of the glass slab.
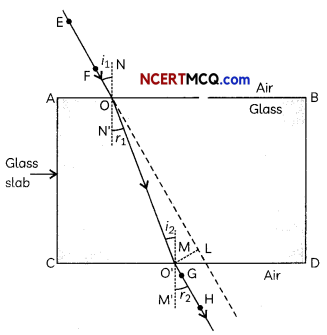
To find the refractive index of two media with respect to each other: Consider three transparent media 1, 2 and 3 having refractive indices n1 n2 and n3 respectively. Then, the refractive index of medium 3 with respect to medium 2 is given as,
n32 = \(\frac{n_{3}}{n_{2}}=\frac{n_{3} / n_{1}}{n_{2} / n_{1}}=\frac{n_{31}}{n_{21}}\) = n31 × n12
![]()
A lens is formed by joining together two refracting surfaces. A transparent material bound by two surfaces, of which one or both surfaces are sphericaL, forms a lens. This means that a lens is bound by at atleast one spherical surface. In such lenses, the other surface would be plane.
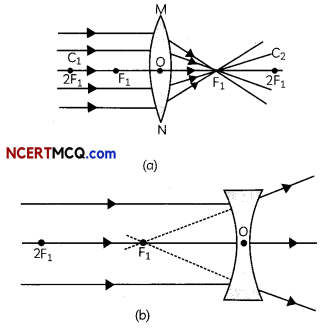
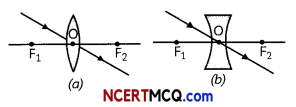
Convex tens: A Lens may have two spherical surfaces. bulging outwards. Such a Lens is called a double convex lens. It is simply called a convex lens. It is thicker at the middle as compared to the edges. Convex Lens converges light rays as shown in Fig. (a). Hence convex tenses are called converging lenses, Concave lens: A double concave tens is bounded by two spherical surfaces. curved inwards. It is thicker at the edges than at the middle. Such lenses diverge light rays as shown in Fig. (b). Such lenses are called diverging lenses. A double concave lens is simply called a concave lens.
A lens, either a convex lens or a concave lens, has two spherical surfaces. Each of these surfaces forms a part of a sphere.
Centre of curvature: The centres of spheres of which the lens is a part are called centres of curvature of the lens. The centre of curvature of a lens is usually represented by the letter C. Since there are two centres of curvature, we may represent them as C1 (2F1)and C2(2F2).
Principal axis: An imaginary straight line passing through the two centres of curvature of a lens is called its principal axis.
Optical centre: The central point of a lens is its optical centre. It is usually represented by the letter O. A ray of light through the optical centre of a lens passes without suffering any deviation.
Aperture: The effective diameter of the circular outline of a spherical lens is called its aperture. Lenses whose aperture is much less than its radius of curvature are called thin lenses with small apertures. If you pass parallel rays from the opposite surface of the lens, you get another principal focus on the opposite side. Letter F is usually used to represent the principal focus. However, a lens has two principal foci. They are represented by F1 and F2.
Focal length: The distance of the principal focus from the optical centre of a lens is called its focal length. The letter f is used to represent the focal length.
To understand the formation of images by a lens, the following rules should be considered:
1. A ray from the object and parallel to the principal. axis posses through the second principal focus F2 (in convex tens) or appears to diverge (in concave tens) from the first principaL focus. F1.
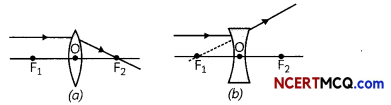
2. A ray of Light passing through the principal focus emerges parallel to the principal axis after refraction from a convex lens. A ray of tight appearing to meet at the principal focus of a concave lens will emerge paraLleL to the principal axis after refraction.
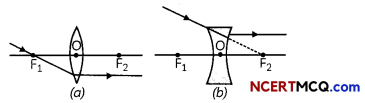
3. A ray of Light passing through the optical centre does not suffer any deviation.
![]()
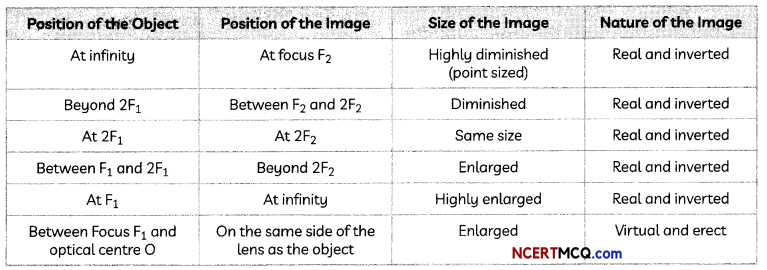
The image formed by a convex lens: The table below lists the position and nature of the image formed by a convex lens for different positions of the object.
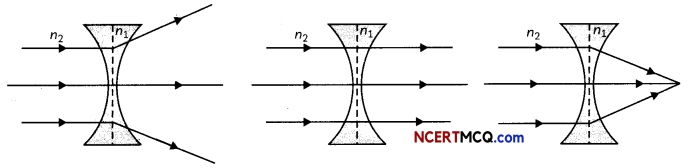
The image formed by a concave Lens:

When a concave lens made of a material of refractive index n1 is kept in a medium of refractive index n2 and a parallel beam of light is incident on the lens, the following figures show the path of rags of Light emerging from the concave Lens if (i) n1 > n2 (ii) n1 = n2 (iii) n1< n2.
Sign Conventions with Spherical Lenses
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\), where
u = object distances
v = image distance
f = Focal length
Magnification produced by a lens: It is defined as the ratio of the size of the image to the size of the object. Thus, magnification, m = \(\frac{\text { Size of image }}{\text { Size of object }}=\frac{h^{\prime}}{h}=\frac{v}{u}\)
Magnification is always positive in case of a concave mirror as it always produces a virtual and erect image.
In case of convex lens, Magnification is positive when the image formed is virtual and negative when image formed is real.
![]()
Example 3.
Which of the following lenses would you prefer to use while reading small letters found in a dictionary?
(a) A convex lens of focal length 50 cm.
(b) A concave lens of focal length 50 cm.
(c) A convex lens of focal length 5 cm.
(d) A concave lens of focal length 5 cm.
Answer:
(c) A convex lens of focal length 5 cm.
Explanation: Convex lens is used for reading small letters found in a dictionary. This is because it magnifies or enlarges the image of the object. As convex lens of shorter focal length has greater power as compared to convex lens of greater focal length, we will use convex lens of focal length 5 cm.
Example 4.
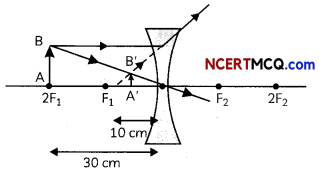
A concave lens of focal length 15 cm forms an image 10 cm from the lens. How far is the object placed from the lens? Draw the ray diagram.
Answer:
Given, f = – 15 cm, v = – 10 cm (minus sign is taken as a concave lens always forms a virtual image).
To find the object distance, we will use the lens formula \(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
Therefore, \(\frac{1}{u}=\frac{1}{v}-\frac{1}{f}=-\frac{1}{10}+\frac{1}{15}\)
\(=\frac{-3+2}{30}=-\frac{1}{30}\) ⇒ u = -30 cm
The object is placed 30 cm in front of the concave lens as shown in the ray diagram:
The power of lens is a measure of the degree of convergence or divergence of light rays falling on it and is defined as the reciprocal of its focal length.
P = \(\frac{1}{f}\)
Dioptre: The SI unit of power of a lens is dioptre (D) and is defined as the power of a lens whose focal length is 1 metre.
Important
The power of a concave lens is negative and that of a convex lens is positive. The power of a lens is more if it has a short focal length.
![]()
Example 5.
A doctor has prescribed a corrective lens of power +1.5 D. Find the focal length of the lens. Is the prescribed lens diverging or converging?
Answer:
The relation between power and focal Length of a lens is given by:
P(in D) = \(\frac{1}{f(\text { in } m)}\) ⇒ f(in m) = \(\frac{1}{P}=\frac{1}{1.5}\) = 0.66
As power (and hence focal length) is positive, the lens is convex having focal length 0.66 m or 66.66 cm.
Power of a combination of lenses: The net power of a combination of lenses is given by the algebraic sum of the individual powers P1 P2, P3,… of the lenses in contact, as
P = P1 + P2 + P3 + ………………..
The use of powers, instead of focal lengths, for lenses is quite convenient for opticians. The simple additive property of the powers of lenses can be used to design lens systems to minimise certain defects in images produced by a single lens. Such a lens system, consisting of several lenses, in contact, is commonly used in the design of camera lenses and the objectives of microscopes and telescopes.
Light is a form of electromagnetic radiation that causes in us a sensation of sight. It also provides us means of communication through optical fiber cables. Several phenomena taking place in nature can be explained by understanding the nature and properties of light.
Reflection of light is the bouncing back of light rays in the same medium on striking a smooth and polished surface.
The reflection of light from mirrors takes place according to the following laws of reflection:
Real image: The image formed by the actual intersection of rays after reflection from the object and which can be obtained on a screen is called a real image.
Virtual image: The image formed if the rays of light after reflection from the object do not actually meet but appear to meet when produced backward and which cannot be obtained on a screen is called a virtual image.
Characteristics of Image Formed by a Plane Mirror
A spherical mirror is a mirror whose reflecting surface is the part of a hollow sphere of glass. A concave mirror is the spherical mirror in which the reflecting surface is the concave or bent-in surface.
A convex mirror is a spherical mirror in which the reflecting surface is the convex or bulging-out surface.
Centre of curvature (C): It is the centre of the hollow sphere of glass of which the mirror is a part. It lies in front of a concave mirror and behind a convex mirror.
Radius of curvature(R): It is the radius of the hollow sphere of glass of which the mirror is part.
Pole (P): The centre of reflection surface of a spherical mirror.
Principal axis: It is the straight line passing through the centre of curvature and pole of a spherical mirror.
Aperture: It is the portion of a mirror from which the reflection of light actually takes place. It represents the size of the mirror. It is the diameter of the reflecting surface of spherical mirror.
Principal focus: The point on the principal axis of the mirror at which the rays of light incident on the mirror in a direction parallel to the principal axis meet after reflection (in case of concave mirror) or appear to diverge after reflection (in case of convex mirror). It is represented by the letter F.
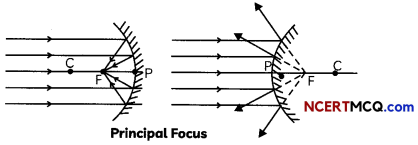
Relation between radius of curvature and focal length: The focal length of a spherical mirror is equal to half of its radius of curvature, i.e., f = R/2.
![]()
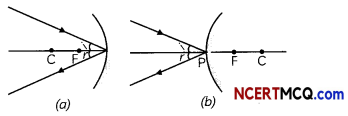
1. The ray parallel to the principal axis after reflec-tion passes through the principal focus F of a concave mirror or appears to pass through the principal focus of a convex mirror.
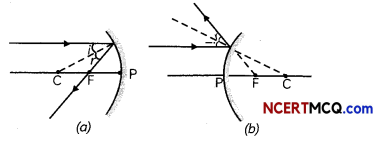
2. A ray passing through the principal focus of a con¬cave mirror or a ray which is directed towards the principal focus of convex mirror becomes parallel to the principal axis after reflection.
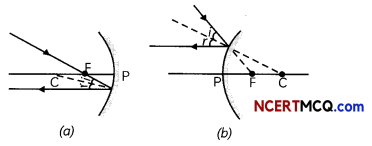
3. A ray passing through the centre of curvature of a concave mirror or directed towards the centre of curvature of convex mirror is reflected back along its own path. The light rays come back along the same path because the incident rays fall on the mirror along the normal to the reflecting surface.
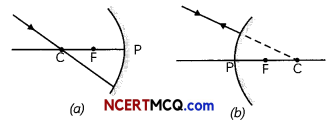
4. A ray incident obliquely to the principal axis at or a convex mirror reflected
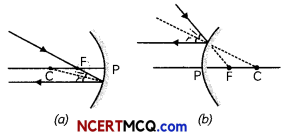
The image formed by a concave mirror: The nature, position and size of the image formed by a plane mirror depends on the position of the object in relation to points P, F and C.

![]()
Example 1.
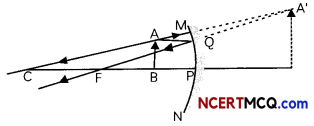
We wish to obtain an erect image of an object, using a concave mirror of focal length 15 cm. What should be the range of distance of the object from the mirror? What is the nature of the image? Is the image larger or smaller than the object? Draw a ray diagram to show the image formation in this case.
Answer:
A concave mirror forms an erect image of an object when the object lies between the pole and focus of the mirror. As the focal length of the concave mirror = 15 cm, therefore, range of distance of the object from the mirror = 0 to less than 15 cm in front of the mirror.
The image formed will be virtual and larger than the object.
Uses of concave mirrors:
Example 2.
Case Based:
In the first activity, take a convex mirror. Hold it in one hand. Hold a pencil in the upright position in the other hand. Observe the image of the pencil in the mirror. Now, move the pencil away from the mirror slowly and repeat this activity carefully.
In the second activity, observe the image of a distant object, say a distant tree, in a plane mirror. Try with plane mirrors of different sizes. Repeat this Activity with a concave mirror. Now try using a convex mirror.
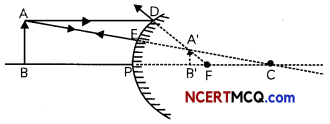
(A) In the first activity, the image of the pencil in the mirror is:
(a) Erect and enlarged
(b) Erect and diminished
(c) Inverted and diminished
(d) Inverted and enlarged.
Answer:
(b) Erect and diminished
Explanation: The image of pencil obtained in the convex mirror is erect and diminished. This is because a convex mirror always forms a virtual, erect and diminished image of an object.
(B) Select the incorrect observation when the pencil is moved away from the mirror slowly:
(I) The image becomes smaller
(II) The image becomes larger
(III) The image moves from the pole towards the focus.
(IV) The image moves farther away from the focus.
(a) Both (I) and (III)
(b) Both (I) and (IV)
(c) Both (II) and (III)
(d) Both (II) and (IV)
Answer:
(d) Both (II) and (IV)
Explanation: As the object is moved slowly away from the convex mirror, the distance of the image of the pencil from the mirror increases i.e., the image shifts from the pole towards the focus and the size of image gradually decreases. When the object is at infinity (very far), the image is at its focus.
(C) Can full length image of a distant object be seen in a plane mirror?
Answer:
No, full length image of a distant object cannot be seen in a plane mirror.
Explanation: Image formed in a plane mirror is of the same size as the object and hence full length image of distant object, such as a tree, cannot be seen in a plane mirror.
(D) Can full length image of a distant object be obtained in a concave mirror?
Answer:
No, full length image of a distant object cannot be seen in a concave mirror.
Explanation: Image formed of a distant object in a concave mirror is diminished due to which we cannot see the full length image of a distant object in a concave mirror.
You can see a full-length image of a tall building/ tree in a small convex mirror. One such mirror is fitted in a wall of Agra Fort. If you visit the Agra Fort, try to observe the full-length image of a distant, tall building/tomb in the wall mirror. To view the tomb distinctly, you should stand suitably at the terrace adjoining the wall.
(E) Assertion (A): Full-length image of a distant object, such as a tall building, can be seen in a convex mir¬ror.
Reason (R): A convex mirror has a greater focal length than a concave mirror of the same aperture.
(a) Both (A) and (R) are true and (R) is the correct explanation of the (A).
(b) Both (A) and (R) are true, but (R) is not the correct explanation of the (A).
(c) (A) is true, but (R) is false.
(d) (A) is false, but (R) is true.
Answer:
(c) (A) is true, but (R) is false.
Explanation: We can obtain Full Length image of a distant object, such as a tall building, can be seen in a convex mirror since a convex mirror always form a virtual and diminished image of an object. Moreover, convex mirror has a wider field of view due to which it is used as rear or side view mirrors in vehicles as distant objects in the backdrop can be seen clearly with much larger field of view.
Image formed by a convex mirror: A convex mirror always forms virtual and diminished image of objects. The image formed by a convex mirror is much smaller than the object which gives the convex mirror a wider field of view.
The image formed by a convex mirror becomes smaller and smaller and will move closer to the focus as the object is moved away from the convex mirror.

![]()
Example 3.
No matter how far you stand from a mirror, your image appears erect. The mirror is likely to be
(a) plane.
(b) concave.
(c) convex.
(d) either plane or convex.
Answer:
(d) either plane or convex.
Explanation: Only plane mirror and convex mirror always form virtual and erect image of object, no matter what the position of the object is.
1. As the position of object shifts from infinity to focus F, the position of image shifts from focus F to Infinity and size of image increases from highly diminished to highly enlarged.
2. When the object is that the focus, the image is at infinity. As the object moves towards the mirror within the focal point the image becomes virtual and upright behind the mirror. Initially the virtual image is much larger than the object and really far away, but as the object approaches the mirror the virtual image also approaches the mirror and decreases in size.
When the object is far away from the mirror the image is upright and located at the focal point. As the object approaches the mirror the image also approaches the mirror and grows until its height equals that of the object.
New Cartesian Sign Conventions for Reflection by Spherical Mirrors
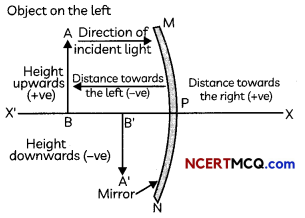
Important
The mirror formula gives a relation between the object distance (u), the image distance (v) and focal length (f) of a spherical mirror.
Mirror formula: \(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
![]()
Example 4.
The magnification produced by a plane mirror is +1. What does this mean?
Answer:
Magnification has two components: the sign denotes whether image is real (minus sign) or virtual (plus sign) and magnitude denotes the relative size of image as compared to the object.
As plane mirror always produces a virtual image, sign is plus. As size of image = size of object, magnitude is 1.
Therefore, magnification produced by a plane mirror is +1 indicates that image formed by a plane mirror is virtual and of same size as object.
Important
Example 5.
A concave mirror produces three times magnified (enlarged) real image of an object placed at 10 cm in front of it. Where is the image located?
Answer:
Magnification produced by a spherical mirror is
defined as m = \(\frac{\text { height of image }}{\text { height of object }}=-\frac{v}{u}\)
Here, m = – 3 (as image is three times magnified and real image).
u = -10 cm.
Therefore, m = \(-\frac{v}{u} \Rightarrow-3=-\frac{v}{-10} \Rightarrow\) v = -30 cm. u = -10
So, the image is located 30 cm in front of the concave mirror.
Example 1.
How are the areas of study evolution and classification – interlinked?
Answer:
The more characteristics two species have in common, the more closely they are related. And they are likely to have a common ancestor more recently. Classification of organisms necessarily involves organizing them in different groups, based on the similarities and differences of characteristics. Classifying organisms helps us in recognizing the basic arrangement of a hierarchical structure among diverse species. It tells us about the similarities and evolutionary relationships between various organisms. Classification of species is a reflection of their evolutionary relationship. Thus, we can say, the areas of study – evolution and classification – interlinked
Tracing Evolutionary Relationships
![]()
Those organs which are similar in structure, have the same developmental origin but perform different functions are known as homologous organs.
Example: forelimbs of mammals, birds, reptiles and amphibians.
The basic structure of the limbs is similar though it has been modified to perform different functions in various vertebrates. Such a homologous characteristic helps to identify an evolutionary relationship between apparently different species.
Those organs which perform similar functions but are structurally dissimilar are known as analogous organs.
Example: Wings of bats and wings of birds.
The wings of bats are skin folds stretched mainly between elongated fingers. But the wings of birds are a feathery covering all along the arm. The designs of the two wings, their structure and components, are very different. They Look similar because they have a common use for flying, but their origins are not common.
Similarly thorns and spines seen in plants are also analogous structures. Both are pointed structures that are protective in function. However, thorn is modification of stem and spine is modified leaf.
Another example of analogous structures in plants is the tendrils of different types carrying out similar function.

Fossils are the preserved traces of living organisms that lived millions of years ago.
Formation of fossils: Usually, when organisms die, their bodies will decompose and be lost. But every once in a while, the body or at least some parts may be in an environment that does not let it decompose completely. If a dead insect gets caught in hot mud, for example, it will not decompose quickly, and the mud will eventually harden and retain the impression of the body parts of the insect.
Analysis of the organ structure in fossils allows us to make estimates of how far back evolutionary relationships go.
Example: The fossil Archaeopteryx is considered to be the connecting link between birds and reptiles as it
has feathered wings and beak (like those of birds) but teeth and tail-like structures (like those of reptiles).
![]()
Example 2.
Explain the importance of fossils in deciding evolutionary relationships.
Answer:
Fossils are the remains or preserved traces of dead plants or animals, which died millions of years ago and some of them are already extinct. The remains or impressions of body part, sometimes can be found between different layers of earth under its surface. The study of fossils have helped us to know about the evolution or the link between two species. Fossils tells us how new species are developed from the old. So fossils have an importance in deciding evolutionary relationship.
Changes in DNA during reproduction are the basic events in evolution. Comparing the DNA of different species give us a direct estimate of how much the DNA has changed during the formation of these species. This method is now extensively used to define evolutionary relationships.
Evolution of Eyes: The complex body organs of animals such as eyes have been created in stages over many generations. Firstly, the rudimentary eye like that of a flatworm (Planaria) was formed, which are very simple and are just eye spots which can detect light. Starting from this basic design, more and more complex eyes were then evolved in various organisms. The evolution of eye is an example of evolution by stages.
Farmers have been cultivating wild cabbage as a food plant for a very long time and have produced or evolved entirely different looking vegetables like cabbage, broccoli, cauliflower, kohlrabi and kale from it by artificial selection.
Evolution is the production of a diversity of life forms and shaping of this diversity by environmental selection due to which more and more complex body designs have emerged. It is not as of when a new species is formed, the old species will disappear.
Note: It is not as if the body designs of older organisms were inefficient.
This is because many of the older and simpler forms of organisms still survive on earth. For example, one of the simplest and primitive life forms called ‘bacteria’ still inhabit some of the most inhospitable (or unfavourable) habitats such as hot springs, deep-sea thermal vents and the ice in Antarctica. Most other organisms cannot survive in such harsh environments.
![]()
Example 3.
In evolutionary terms, can we say which among bacteria, spiders, fish and chimpanzees have a ‘better’ body design? Why or why not?
Answer:
In evolutionary terms, we can not say which among bacteria, spiders, fish and chimpanzees have a ‘better’ body design. Because the evolutionary process takes into account the development of most efficient and suitable features in body designs of organisms for survival and adaptation favoring to a particular niche. For example, organisms with Complex and seemingly better body design, may not survive particular situations. Whereas, organisms like bacteria with its primitive body design and simple microbial life form may survive in the most inhospitable and extreme environmental conditions that are extraordinarily hot, cold or acidic.
Molecular phylogeny: Changes in the DNA during cell division would lead to changes in the proteins that are made from this new DNA and these changes would accumulate from one generation to the next. The idea behind molecular phylogeny is based on the idea that organisms that are more distantly related will accumulate a greater number of differences in their DNA. Such studies trace the evolution.