Category: Uncategorized

NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2.

Board	CBSE
Textbook	NCERT
Class	Class 10
Subject	Maths
Chapter	Chapter 11
Chapter Name	Constructions
Exercise	Ex 11.2
Number of Questions Solved	7
Category	NCERT Solutions

NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2

In each of the following, give the justification of the construction also:

Question 1.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.
Solution:
Steps of Construction:
1. Draw a circle of radius 6 cm.
2. Mark a point P at a distance 10 cm from the centre O.
3. Here OP = 10 cm, draw perpendicular bisector of OP, which intersects OP at O’.
4. Take O’ as centre, draw a circle of radius O’O, which passes through O and P and intersects the previous circle at points T and Q.
5. Join PT and PQ, measure them, these are the required tangents.

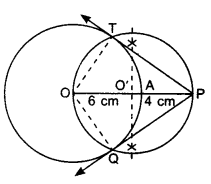
Justification:
Join OT and OQ.

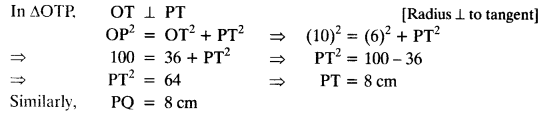
A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ PT = PQ.

Question 2.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Solution:
Steps of Construction:
1. Draw concentric circles of radius OA = 4 cm and OP = 6 cm having same centre O.
2. Mark these circles as C and C’.
3. Points O, A and P lie on the same line.
4. Draw perpendicular bisector of OP, which intersects OP at O’.
5. Take O’ as centre, draw a circle of radius OO’ which intersects the circle C at points T and Q.
6. Join PT and PQ, these are the required tangents.
7. Length of these tangents are approx. 4.5 cm.

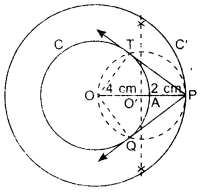
Justification:
Join OT and OQ.

A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ PT = PQ.

Question 3.
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Solution:
Steps of Construction:

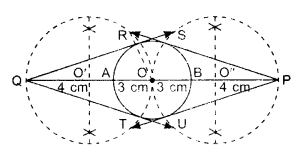
1. Draw a circle of radius 3 cm, having centre O. Mark this circle as C.
2. Mark points P and Q along its extended diameter such that OP = 7 cm and OQ = 7 cm.
3. Draw perpendicular bisector of OQ, intersecting OQ at O’.
4. Draw perpendicular bisector of OP intersecting OP at O”.
5. Take O’ as centre and draw a circle of radius OO’ which passes through points O and Q, intersecting circle C at points R and T.
6. Take O” as centre and draw a circle of radius O”P which passes through points O and P, intersecting the, circle C at points S and U.
7. Join QR and QT; PS and PU, these are the required tangents.
Justification:
Join OR.
In ∆OQR,
OR ⊥ QR [Radius ± to tangent]
OQ² = OR² + QR²
⇒ (7)² = (3)² + QR² ⇒ 49 = 9 + OR²
⇒ 40 = QR² ⇒ QR = 2 \(\sqrt{10}\) cm
Similary,
QT = 2 \(\sqrt{10}\) cm
PS = 2 \(\sqrt{10}\) cm
PU = 2 \(\sqrt{10}\) cm
A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ QR = QT and PS = PU

Question 4.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other at an angle of 60°.
Solution:
Steps of Construction:

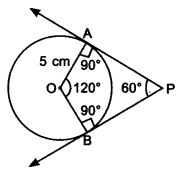
1. Draw a circle of radius 5 cm.
2. As tangents are inclined to each other at an angle of 60°.
∴ Angle between the radii of circle is 120°. (Use quadrilateral property)
3. Draw radii OA and OB inclined to each other at an angle 120°.
4. At points A and B, draw 90° angles. The arms of these angles intersect at point P.
5. PA and PB are the required tangents.
Justification:
In quadrilateral AOBP,
AP and BP are the tangents to the circle.
Join OP.
In right angled AOAP, OA ⊥ PA [Radius is ⊥ to tangent]

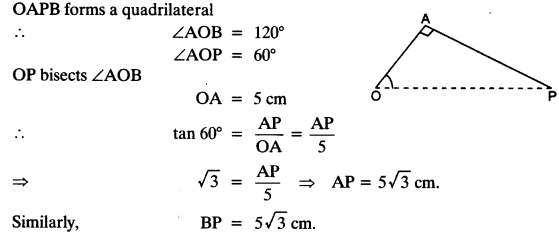
A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ PA = PB

Question 5.
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution:
Steps of Construction:

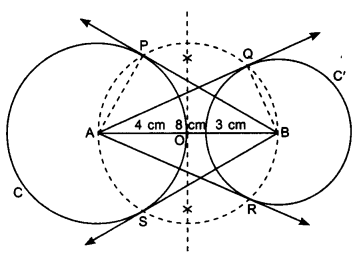
1. Draw a line segment AB = 8 cm.
2. Taking A as centre draw a circle C of radius 4 cm and taking B as centre draw a circle C’ of radius 3 cm.
3. Draw perpendicular bisector of AB, which intersects AB at point O.
4. Taking point O as centre draw a circle of radius 4 cm passing through points A and B which intersect circle C at P and S and circle C’ at points R and Q.
5. Join AQ, AR, BP and BS. These are the required tangents.
Justification:
Join AP.

A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ AQ = AR and BP = BS.

Question 6.
Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and ZB = 90°. BD is the perpendicular Burn B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Solution:
Steps of Construction:
1. Draw a right triangle ABC with AB = 6 cm, BC = 8 cm and ZB = 90°.
2. From B, draw BD perpendicular to AC.
3. Draw perpendicular bisector of BC which intersect BC at point O’.
4. Take O’ as centre and O’B as radius, draw a circle C’ passes through points B, C and D.

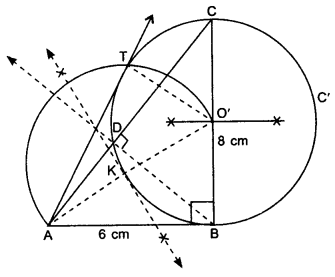
5. Join O’A and draw perpendicular bisector of O’A which intersect O’A at point K.
6. Take K as centre, draw an arc of radius KO’ intersect the previous circle C’ at T.
7. Join AT, AT is required tangent.
Justification:
∠BDC = 90°
∴ BC acts as diameter.
AB is tangent to circle having centre O’

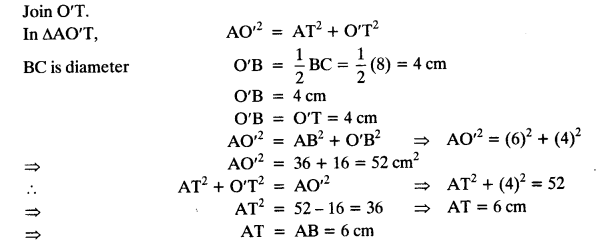
A pair of tangents can be drawn to a circle from an external point outside the circle. These two tangents are equal in lengths.
∴ AB = AT.

Question 7.
Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Solution:
Steps of Construction:
1. Draw a circle C’ with the help of a bangle, for finding the centre, take three non-collinear points A, B and C, lying on the circle. Join AB and BC and draw perpendicular bisector of AB and BC, both intersect at a point O,
‘O’ is centre of the circle.

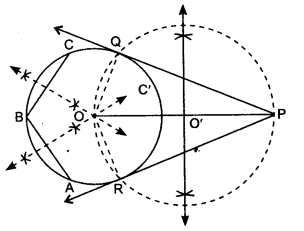
2. Take a point P outside the circle. Join OP.
3. Draw perpendicular bisector of OP, which intersects OP at point O’.
4. Take O’ as the centre with OO’ as radius draw a circle which passes through O and P, intersecting previous circle C’ at points R and Q.
5. Join PQ and PR.
6. PQ and PR are the required pair of tangents.
Justification:
Join OQ and OR.
In AOQP and AOPR, OQ = OR [Radii of the circle]
OP = OP [Common]
∠Q = ∠R = 90° [Radius is ⊥ to tangent]
∆OQP ≅ ∆ORP [by RHS]
∴ PQ = PR [By C.P.C.T]
A pair of tangents can be drawn to a circle from an external point lying outside the circle. These two tangents are equal in lengths.
∴ PQ = PR

We hope the NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2 help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 11 Constructions Ex 11.2, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.1 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.1.

Board	CBSE
Textbook	NCERT
Class	Class 10
Subject	Maths
Chapter	Chapter 14
Chapter Name	Statistics
Exercise	Ex 14.1
Number of Questions Solved	9
Category	NCERT Solutions

NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.1

Question 1.
A survey was conducted by a group of students as a part of their environment awareness programme, in which they collected the following data regarding the number of plants in 20 houses in a locality. Find the mean number of plants per house.

Which method did you use for finding the mean, and why?
Solution:

Since the values of x_i and f_i are small, so we have used direct method to find the mean.

Question 2.
Consider the following distribution of daily wages of 50 workers of a factory.

Find the mean daily wages of the workers of the factory by using an appropriate method.
Solution:
Here h = 20

Question 3.
The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is ₹ 18. Find the missing frequency f.

Solution:

Question 4.
Thirty women were examined in a hospital by a doctor and the number of heart beats per minute were recorded and summarised as follows. Find the mean heart beats per minute for these women, choosing a suitable method

Solution:

Question 5.
In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained varying number of mangoes. The following was the distribution of mangoes according to the number of boxes.

Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose?
Solution:
Here h = 3

Step deviation method.

Question 6.
The table below shows the daily expenditure on food of 25 households in a locality.

Find the mean daily expenditure on food by a suitable method.
Solution:

Question 7.
To find out the concentration of SO₂ in the air (in parts per million, i.e. ppm), the data was collected for 30 localities in a certain city and is presented below:

Find the mean concentration of SO₂ in the air.
Solution:
Here h = 0.04

Question 8.
A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.

Solution:

Question 9.
The following table gives the literacy rate (in percentage) of 35 cities. Find the mean literacy rate.

Solution:
Here h = 10

We hope the NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.1, help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 14 Statistics Ex 14.1, drop a comment below and we will get back to you at the earliest.

NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.4 are part of NCERT Solutions for Class 10 Maths. Here we have given NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.4.

Board	CBSE
Textbook	NCERT
Class	Class 10
Subject	Maths
Chapter	Chapter 13
Chapter Name	Surface Areas and Volumes
Exercise	Ex 13.4
Number of Questions Solved	5
Category	NCERT Solutions

NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.4

Unless stated otherwise, take π = \(\frac { 22 }{ 7 }\)

Question 1.
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular .ends are 4 cm and 2 cm. Find the capacity of the glass.
Solution:
Given: upper diameter = 4 cm ⇒ upper radius = \(\frac { 1 }{ 2 }\) = 2 cm = R
lower diameter = 2 cm ⇒ lower radius = \(\frac { 2 }{ 2 }\) = 1 cm = r
height of glass = 14 cm

Question 2.
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Solution:
Given: upper circumference of the frustum = 18 cm

Slant height (l) = 4 cm
We have C.S.A of the frustum = π (r₁ + r₂)l
Putting values from equation (i) and (ii), we get
Curved surface area = (πr₁ + πr₂)l = (9 + 3) x 4 = 12 x 4 = 48 cm²

Question 3.
A fez, the cap used by the Turks, is shaped like the frustum of a cone (see figure). If its radius on the open side is 10 cm, radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it.

Solution:
Radius of open side (r₁) = 10 cm
Radius of upper base (r₂) = 4 cm
Slant height (l) = 15 cm

Total surface area of the cap = C.S.A. of the frustum + Area of upper base
= 660 cm² + 50.28 cm² = 710.28 cm²

Question 4.
A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of ₹ 20 per litre. Also find the cost of metal sheet used to make the container, if it costs ₹ 8 per 100 cm2. (Take π = 3.14)
Solution:
Radius of the lower end (r₁) = 8 cm
Radius of the upper end (r₂) = 20 cm
Height of the frustum (h) = 16 cm

Question 5.
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter \(\frac { 1 }{ 16 }\) cm, find the length of the wire.
Solution:
Let ADC is a cone with vertical angle 600.
Now, cone is cut into two parts, parallel to its base at height 10 cm.
Radius of larger end of the frustum = R₁

A wire be formed having diameter \(\frac { 1 }{ 16 }\) cm and length be H cm
Volume of wire so obtained = πr²H

We hope the NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.4, help you. If you have any query regarding NCERT Solutions for Class 10 Maths Chapter 13 Surface Areas and Volumes Ex 13.4, drop a comment below and we will get back to you at the earliest.

ML Aggarwal Class 8 Solutions for ICSE Maths Model Question Paper 4

Choose the correct answer from the given four options (1-2):
Question 1.
\(\frac{103^{2}-97^{2}}{200}\) is equal to
(a) 3
(b) 4
(c) 5
(d) 6
Solution:

Question 2.
If the’ sum of three consecutive even integers is 36, then the largest integer is
(a) 10
(b) 12
(c) 14
(d) 16
Solution:

Question 3.
Find the area of rectangle whose length and breadth are respectively (4x² – 3x + 7) and (3 – 2x + 3x²).
Solution:

Question 4.
Factorize: a² – c² – 2ab + b².
Solution:

Question 5.
The ages of A and B are in the ratio 3 : 4. Five years later the sum of their ages will be 31 years. What are their present ages?
Solution:

Question 6.
The sum of the digits of a two-digit number is 13. If the number obtained by reversing the digits is 45 more than the original number. Find the original number.
Solution:

Question 7.
The ratio between an exterior angle and interior angle of a regular polygon is 1 : 5, find:
(i) the measure of each exterior angle,
(ii) the measure of each interior angle.
(iii) the number of sides of the polygon.
Solution:

Question 8.
Solve the inequality: 3 – \(\frac{x}{2}\) > 2 – \(\frac{x}{3}\) , x ϵ W.
Also represent its solution set on the number line.
Solution:

Question 9.
Factorise: x² + \(\frac{1}{x^{2}}-7\left(x-\frac{1}{x}\right)\) + 8.
Solution:

Question 10.
In the given figure, ABCD is a parallelogram. Find x, y, z and w.

Solution:

ML Aggarwal Class 8 Solutions for ICSE Maths

Selina Publishers Concise Biology Class 8 ICSE Solutions Chapter 4 Ecosystems

Selina Concise Biology Class 8 ICSE Solutions

CBSE Sample Papers for Class 10 Social Science Paper 2 are part of CBSE Sample Papers for Class 10 Social Science. Here we have given CBSE Sample Papers for Class 10 Social Science Paper 2.

CBSE Sample Papers for Class 10 Social Science Paper 2

Board	CBSE
Class	X
Subject	Social Science
Sample Paper Set	Paper 2
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 2 of Solved CBSE Sample Paper for Class 10 Social Science is given below with free PDF download solutions.

General Instructions:   

• The question paper has 27 questions in all. All questions are compulsory.
• Marks are indicated against each question.
• Questions from serial number 1 to 7 are very short answer questions. Each question carries 1 mark.
• Questions from serial number 8 to 18 are 3 marks questions. Answer of these questions should not exceed 80 words each.
• Questions from serial number 19 to 25 are 5 marks questions. Answer of these questions should not exceed 100 words each.
• Question number 26 and 27 are map questions of 2 marks from History and 3 marks from Geography. After completion, attach the maps inside the answer book

Question 1.
What was ‘cowries’?
OR
Who produced a music book that had a picture on the cover page announcing the ‘Dawn of the Century’?
OR
Who wrote several volumes on the London labour, and compiled long lists of those who made a living from crime?

Question 2.
Name the oldest Japanese book printed.
OR
What was the price of Henry Fielding’s Tom Jones (1749) issued in six volumes?

Question 3.
What do you understand by The Black Power?

Question 4.
Give a prominent example of a region with a low rainfall and which is drought prone.

Question 5.
What does development mean for a landless rural labourer?

Question 6.
What is a cheque?

Question 7.
What does Life Expectancy at birth denote?

Question 8.
Gandhiji decided to launch a nationwide satyagraha in 1919. Why?

Question 9.
Critically evaluate the conditions that favoured the conquests of Latin America by the European
powers like Spain and Portugal.
OR
What is proto-industrialisation? “In the seventeenth and eighteenth centuries, merchants from the towns in Europe began moving to the countryside”. Explain any two reasons.
OR
Who wrote ‘The Bitter Cry of Outcast London’? When? What was the issue author stated?

Question 10.
What is holding together Federation? Give examples of ‘holding together federations’.

Question 11.
What are Concurrent Lists? Give Examples.

Question 12.
Point out why the Mexico Olympics of 1968 was depicted as a landmark in the history of the
Civil Rights Movements in the United States of America.

Question 13.
Define the term resource. Do you think resources are free gift of nature?

Question 14.
Name the two important by-products of sugarcane other than the sugar and jaggery. State
the temperature and rainfall requirements of sugarcane. Also name the two major sugarcane producing states of India.

Question 15.
What is ‘Average Income’ Or ‘Per capita Income’?

Question 16.
Analyse the functions of Consumer Protection Councils?

Question 17.
Explain what is tertiary sector? Give examples.

Question 18.
Who supervises the functioning of banks? In what ways is the supervision done?

Question 19.
Write short notes on Gutenberg and the Printing Press.
OR
‘The most of readers of the novel lived in the city, the novel created in them a feeling of connection with the fate of rural communities’. Explain with suitable examples

Question 20.
From which language the term ‘liberalism’ derived? Give its meaning. What was liberalism
according to Middle Class?
OR
Why the French thought colonies necessary? What did they do for that? Explain any two points.

Question 21.
‘Democracy is an accountable, responsive and legitimate form of government’. Explain

Question 22.
Discuss Challenge of Expansion and Challenge of Deepening of Democracy with suitable
examples.

Question 23.
What is the total length of road networks in India? Explain how roads have edge over the
railways.

Question 24.
Name the most important metallurgical industry in India. Where is this industry concentrated?
Explain any two factors responsible for the concentration of this industry.

Question 25.
Explain any two rights of consumers that protect them from exploitation in the market place.

Question 26.
Two features A and B are marked on the given political outline map of India: Identify these features with the help of the following information and write their correct names on the lines marked in the map:
A. The place where the Indian National Congress Session was held in September 1922.
B. The place where Gandhiji broke the ‘Salt Law’.
OR
Locate and label on the same map given:
(1) The place where peasants organized a Satyagraha in 1917
(2) Nagpur

Question 27.
On the given same political outline map of India locate and label/identify the type of soil the following with appropriate symbols:
(1) Identity the type of soil in the shaded portion shown in map.
(2) Mysore Silk Textile Centre
(3)Vishakhapatnam Sea Port

Answers

Answer 1.
Cowries-the Hindi cowdi or seashells, used as a form of currency.
OR
In 1900, a popular music publisher E.T. Pauli.
OR
Henry Mayhew.

Answer 2.
The oldest Japanese book, printed in AD 868, is the Buddhist Diamond Sutra.
OR
Henry Fielding’s Tom Jones (1749) was issued in six volumes priced at three shillings each.

Answer 3.
A movement emerged in 1966 and lasted till 1975, which was a more militant anti-racist
movement, advocating even violence if necessary to end racism in the US.

Answer 4.
Rajasthan

Answer 5.
Ans. More days of work and better wages; local school is able to provide quality education for
children; there is health facilities, and there is no social discrimination.

Answer 6.
A cheque is a paper instructing the bank to pay a specific amount from the person’s account
to the person in whose name the cheque has been issued.

Answer 7.
Life Expectancy at birth denotes, as the name suggests, average expected length of life of a
person at the time of birth.

Answer 8.
(1) Gandhij i in 1919 decided to launch a nationwide satyagraha against the proposed Rowlatt Act (1919).
(2) This Act had been hurriedly passed through the Imperial Legislative Council despite the united opposition of the Indian members. It gave the government enormous powers to repress political activities, and allowed detention of political prisoners without trial for two years.
(3) Mahatma Gandhi wanted non-violent civil disobedience against such unjust laws, which would start with a hartal on 6 April.

Answer 9.
(1) The conquest by European powers like Spain and Portugal were not just a result of superior
firepower or conventional military weapons.
(2) It was the germs such as those of smallpox that they carried on their person. Because of their long isolation, America’s original inhabitants had no immunity against these diseases
that came from Europe. Smallpox in particular proved a deadly killer.
(3) Once introduced, it spread deep into the continent, ahead even of any Europeans reaching there. It killed and decimated whole communities, paving the way for conquest.
OR
Even before factories began to dot the landscape in England and Europe, there was large- scale industrial production for an international market. This was not based on factories. Many historians now refer to this phase of industrialisation as proto-industrialisation.
Two Reasons:

• In the seventeenth and eighteenth centuries, merchants from the towns in Europe began moving to the countryside, supplying money to peasants and artisans, persuading them to produce for an international market.
• With the expansion of world trade and the acquisition of colonies in different parts of the world, the demand for goods began growing.

OR
1. Andrew Meams, a clergyman who wrote The Bitter Cry of Outcast London in the 1880s.
2. It showed why crime was more profitable than labouring in small underpaid factories: ‘A child seven years old is easily known to make 10 shillings 6 pence a week from thieving … Before he can gain as much as the young thief (a boy) must make 56 gross of matchboxes a week, or 1,296 a day.

Answer 10.
Holding Together is where a large country decides to divide its power between the constituent
States and the national government. In this category, the central government tends to be more powerful vis-a-vis the States. Very often different constituent units of the federation have unequal powers. Some units are granted special powers.
India, Spain and Belgium are examples of this kind of ‘holding together’ federations.

Answer 11.
(1) Concurrent List includes subjects of common interest to both the Union Government as
well as the State Governments, such as education, forest, trade unions, marriage, adoption and succession.
(2) Both the Union as well as the State Governments can make laws on the subjects mentioned in this list. If their laws conflict with each other, the law made by the Union Government will prevail.

Answer 12.
(1) The US athletes, Tommie Smith and John Carlos were African-Americans. They had won the gold and bronze medals respectively.
(2) They received their medals wearing black socks and did not wear shoes, this was done to represent Black poverty. With this gesture, they tried to draw international attention to racial discrimination in the United States.
(3) The black-gloved and raised clenched fists were meant to symbolize black power. The silver medallist, white Australian athlete, Peter Norman, wore a human rights badge on his shirt during the ceremony to show his support to the two Americans

Answer 13.
(1) Everything available in our environment which can be used to satisfy our needs, provided,
it is technologically accessible, economically feasible and culturally acceptable can be termed as ‘Resource’.
(2) They are not. Resources are a function of human activities.
(3) Human beings themselves are essential components of resources.
(4) They transform material available in our environment into resources and use them.

Answer 14.
(1) Sugarcane by-products: Khandsari and molasses
(2) Rainfall: 75-100 cm annually
(3) Temperature: 21°C to 27°C
(4) States: Uttar Pradesh, Maharashtra, Tamil Nadu and Karnataka, Punjab and Haryana.

Answer 15.
Per capita Income is obtained by dividing the national income by the population of the country.

Answer 16.
(1) The consumer movement in India has led to the formation of various organisations locally known as consumer forums or consumer protection councils.
(2) They guide consumers on how to file cases in the consumer court. On many occasions,
they also represent individual consumers in the consumer courts.
(3) These voluntary organisations also receive financial support from the government for
creating awareness among the people.

Answer 17.
(1) These are activities that help in the development of the primary and secondary sectors.
These activities, by themselves, do not produce a good but they are an aid or a support
for the production process.
(2) For example, goods that are produced in the primary or secondary sector would need to be transported by trucks or trains and then sold in wholesale and retail shops. At times, it may be necessary to store these in godowns.
(3) We also may need to talk to others over telephone or send letters (communication) or
borrow money from banks (banking) to help production and trade. Transport, storage, communication, banking, trade are some examples of tertiary activities.
(4) Since these activities generate services rather than goods, the tertiary sector is also called the service sector.

Answer 18.
(1) The Reserve Bank of India supervises the functioning of formal sources of loans.
(2) The RBI monitors the banks whether they are maintaining minimum cash balance.
(3) The RBI sees that the banks give loans not just for profit-making businesses and traders
but also to small cultivators, small scale industries, to small borrowers etc.
(4) Periodically, banks have to submit information to the RBI on how much they are lending, to whom, at what interest rate, etc.

Answer 19.
(1) Gutenberg was the son of a merchant and grew up on a large agricultural estate.
(2) From his childhood he had seen wine and olive presses. He learnt the art of polishing i stones, became a master goldsmith, and also acquired the expertise to create lead moulds used for making trinkets. Drawing on this knowledge, Gutenberg adapted existing
technology to design his innovation. The olive press provided the model for the printing press, and moulds were used for casting the metal types for the letters of the alphabet.
(3) By 1448, Gutenberg perfected the system. The first book he printed was the Bible. About 180 copies were printed and it took three years to produce them. By the standards of the time this was fast production.
OR
(1) The nineteenth-century British novelist Thomas Hardy, for instance, wrote about traditional rural communities of England that were fast vanishing. It was written at a time when large farmers fenced off land, bought machines and employed labourers to produce for the market.
(2) Second was when the old rural culture with its independent farmers was dying out. We get a sense of this change in Hardy’s Mayor of Casterbridge (1886). It is about Michael Henchard, a successful grain merchant, who becomes the mayor of the farming town of Casterbridge.

Answer 20.
(1) The term ‘liberalism’ derives from the Fatin root liber, meaning free.
(2) For the new middle classes, liberalism stood for freedom for the individual and equality of all before the law.
(3) Politically, it emphasised the concept of government by consent. Since the French Revolution, liberalism had stood for the end of autocracy and clerical privileges, a constitution and representative government through parliament. Nineteenth-century liberals also stressed the inviolability of private property.
OR
(1) Colonies were considered essential to supply natural resources and other essential goods.
(2) Fike other Western nations, France also thought it was the mission of the ‘advanced’ European countries to bring the benefits of civilisation to backward peoples.
(3) The French began by building canals and draining lands in the Mekong delta to increase cultivation. The vast system of irrigation works – canals and earthworks – built mainly with forced labour, increased rice production and allowed the export of rice to the international market.

Answer 21.
(1) Most basic outcomes of democracy should be that it produces a government that is
accountable to the citizens, and responsive to the needs and expectations of the citizens.
(2) Democracy is based on the idea of deliberation and negotiation. So, some delay is bound to take place but because it has followed procedures, its decisions may be both more acceptable to the people and more effective. So, the cost of time that democracy pays is perhaps worth it.
(3) A citizen who wants to know if a decision was taken through the correct procedures can find this out. She has the right and the means to examine the process of decision-making. This is known as transparency.
(4) The democratic government develops mechanisms for citizens to hold the government accountable and mechanisms for citizens to take part in decision making whenever they think fit.

Answer 22.
Discuss Challenge of Expansion and Challenge of Deepening of Democracy with suitable
examples.
Ans.
(1) Challenge of ‘Expansion of Democracy’: This stage involves applying the basic principle of democratic government across all the regions, different social groups and various institutions. Empowering various social groups, federal structures, women and minorities etc. This also means that less and less decisions should remain outside the democratic control. Most of the democracies like India and USA face this challenge.
(2) Challenge of ‘Deepening of Democracy’: This involves strengthening of the institutions and practices of democracy by people’s participation and control. This should happen in such a way that people can realise their expectations of democracy. This requires an attempt to bring down the control and influence of the rich and powerful in making governmental decisions.

Answer 23.
(1) Length of road networks: 2.3 million km.
(2) Roadways: Edge over railways: (Any three)

• Construction cost of roads is much lower than that of railway lines.
• Roads can traverse comparatively more dissected and undulating topography.
• Roads can negotiate higher gradients of slopes and as such can traverse mountains such
  as the Himalayas.
• Road transport is economical in transportation of few persons and relatively smaller amount of goods over short distances.
• It also provides door-to-door service, thus the cost of loading and unloading is much lower.
• Road transport is also used as a feeder to other modes of transports such as they provide a link between railway stations, air and seaports.

Answer 24.
(1) Iron and Steel industry
(2) Chhotanagpur Plateau region
(3) Factors responsible:
(a) Low cost iron ore: Chhotanagpur Plateau region is extremely rich in good quality iron ore at low cost. This helped to locate many steel plants in this region.

(b) Home market: India is progressing rapidly. Hence, the country is in great need of steel leading to a great demand. Thus, there is a great potential for home market.

(c) Well developed transport network: This region is well developed has network of railways and that helps procuring raw materials and then distribute in the market.

Answer 25.
Rights of consumers:

1. Right to information
2. Right to seek redressal
3. Right to choose
4. Right to be heard
5. Right to safety

Answer 26.

Answer 27.

We hope the CBSE Sample Papers for Class 10 Social Science Paper 2 help you. If you have any query regarding CBSE Sample Papers for Class 10 Social Science Paper 2, drop a comment below and we will get back to you at the earliest.

These Sample papers are part of CBSE Sample Papers for Class 12 History Here we have given CBSE Sample Papers for Class 12 History Paper 7.

CBSE Sample Papers for Class 12 History Paper 7

Board	CBSE
Class	XII
Subject	History
Sample Paper Set	Paper 7
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 7 of Solved CBSE Sample Paper for Class 12 History is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 80

General Instructions

(i) Answer all the questions. Some questions have internal choice. Marks are indicated against each question.
(ii) Answer to question nos 1 to 3 carrying 2 marks should not exceed 30 words each.
(in’) Answer to question nos. 4 to 9 carrying 4 marks should not exceed 100 words. Students should attempt only 5 questions in this section.
(iv) Question 10 (for 4 marks) is a value based question and compulsory question.
(v) Answer to question nos 11 to 13 carrying 8 marks should not exceed 350 words.
(vi) Questions 14 – 16 are source based questions and have no internal choice.
(vii) Question 17 is a map question includes ‘identification’ and significant’ test items.

PART-A

Answer all the questions given below:

Question 1:
Write any two similarities between Jainism and Buddhism.

Question 2:
Akbar was impressed by Abul Fazl. Why?

Question 3:
Mention two features of the Indian constitution.

PART-B
Section-I

Answer any five of the following questions:

Question 4:
How did Asoka propagate and spread Buddhism?

Question 5:
“The rules of the Brahamanical text were not universally followed in ancient time”. Justify the statement.

Question 6:
Discuss the basic principles of Islam.

Question 7:
Discuss the Lotus Mahal and Hazara Ram temple of Vijayanagara.

Question 8:
Explain the Subsidiary Alliance.

Question 9:
Why did British Government give special focus on mapping?

Section-II

Value Based Question

Question 10:
Read the following passage and answer the question that follow.

“Sons were important for the continuity of the patrilineage, daughters were viewed rather differently within this framework. They had no claims to the resources of the household. Women do not entertain equal status in the society for a long period. What type of values should be followed to consider them equal.

PART – C

Answer all the questions given below:

Question 11:
Explain the important features of the religion of Harappan culture which are still prevalent.
OR
Discuss the emergence and teachings of Jainism.

Question 12:
How did A1 Biruni describe the caste system?
OR
Explain the aspects of the Mughal period which are highlighted by Abul Fazl’s Ain-l-Akbari?

Explain political life of Mahatma Gandhi.
OR
Discuss the genesis and development of Hindu Communalism.

PART – D

Source Based Questions

Question 14:
Read the following excerpt carefully and answer the questions that follows.

What the King’s Officials did

Here is an excerpt from the account of Megasthenes: Of the great officers of state, some … superintend the rivers, measure the land, as is done in Egypt, and inspect the sluices by which water is let out from the main canals into their branches, so that everyone may have an equal supply of it. The same persons have charge also of the huntsmen, and are entrusted with the power of rewarding or punishing them according to their desires. They collect the taxes, and superintend the occupations connected with land; as those of the woodcutters, the carpenters, the blacksmiths, and the miners.

1. Mention any three features of the Mauryan administration under Asoka.
2. Write the jobs done by the officers of the state.
3.  What are the other sources for studying the empire?

Question 15:
Read the following excerpt carefully and answer the questions that follow.

Kings and Traders

Krishnadeva Raya (ruled 1509-29), the most famous ruler of Vijayanagara, composed a work on statecraft in Telugu known as the Amuktamalyada. About traders he wrote: A king should improve the harbours of his country and so encourage its commerce that horses, elephants, precious gems, sandalwood, pearls and other articles are freely imported … He should arrange that the foreign sailors who land in his country on account of storms, illness and exhaustion are looked after in a suitable manner… Make the merchants of distant foreign countries who import elephants and good horses be attached to yourself by providing them with daily audience, presents and allowing decent profits. Then those articles will never go to your enemies.

1. Which item of import was most important and why?
2.  Why was trade important to the king?
3. Write three measures the king suggested for encouraging trade.

Question 16:
Read the following excerpt carefully and answer the questions that follow.

On that day in Supa

On 16 May 1875, the District Magistrate of Poona wrote to the Police Commissioner: On arrival at Supa on Saturday 15 May I learnt of the disturbance. One house of a moneylender was burnt down; about a dozen were forcibly broken into and completely gutted of their content. Account papers, bonds, grains, country cloth were burnt in the street where heaps of ashes are still to be seen. The chief constable apprehended 50 persons. Stolen property worth ₹2000 was recovered. The estimated loss is over ₹ 25,000. Moneylenders claim it is over 1 lakh.

1.  Mention the pattern that was seen in places where the revolt spread.
2. How did the British react?
3.  Why did the Ryotwari system in the Deccan lead to revolts?

PART-E

Map Questions

Question 17:
17.1. On the given outline map of India, locate and label the following with appropriate symbols.
(a) Kingdom of Cheras
(b) Nasik – A Buddhist site

17.2. On the same outline map of India three centres related to Indian National movement have been marked as A, B and C. Identify them and write their correct names on the lines drawn near them.

Answers

Answer 1:
(i) Both the religions were founded by Princes. Both were kshatriyas and they left home in search of truth.
(ii) The aim of both the religions was salvation.

Answer 2:
(i) Abul Fazl was an independent thinker. He always opposed the orthodox views of ulemas.
(ii) Akbar was very much impressed by these traits of Abul Fazl. He found Abul Fazl as an appropriate person and as a spokesperson of his policies and as his advisor.

Answer 3:
(i) Granting the right to vote to every adult citizen of India. It was called the universal adult franchise.
(ii) Emphasis on secularism. It is the soul of the Indian constitution.

Answer 4:
(i) Kalinga war changed Asoka. He left the policy of war and gave his heart and soul in spreading and propagating Buddhism. He also followed the rules which he propagated.
(ii) Asoka engraved all rules about the religion of Buddhism on the inscriptions, stones, caves. The rules were engraved in the language of common masses so that it could be Understand.
(iii) He built many stupas and viharas which became centres of Buddhism. He provided economic help to all the Buddhist monasteries.
(iv) Asoka made journey to Buddhist pilgrims. He sent his son Mahendra and daughter Sanghamitra to Sri Lanka to propagate Buddhism. Asoka moulded Buddhism into a world religion.

Answer 5:
(i) The women would give up their gotra after their marriage and adopt the gotra of their husband. The Satavahana queens did not do so.
(ii) According to the Brahmanical books, only the Kshatriyas could be the rulers, but many Brahmans and Vaishyas were also the rulers.
(iii) Many classes were there whose profession did not match the vama system. Nishad and nomadic people reared the cattle.
(iv) Marriages were solemnized outside the caste system, though the Brahmanical books did not permit them.
On the basis of sex, the right to property was often given to the men; whereas Prabhavati Gupta enjoyed the right to property.

Answer 6:
These principles are accepted as the five pillars of faith by the followers of Islam.
(i) Allah is one God. Prophet Mohammad is the messenger of Allah and Holy Quran is the order of Allah.
(ii) The followers of Islam should offer prayers five times a day. It is known as Namaz.
(iii) They should give alms (Zakat) to the poor.
(iv) The followers of Islam keep fast during the month of Ramzan.
(v) Followers of Islam should go on a pilgrimage to Mecca once in their lives.

Answer 7:
Lotus Mahal:

(i) The royal centre of Vijaynagara had a very beautiful building. It was called the Lotus Mahal by a British traveller in the 19th century.
(ii) Many historians are not clear still about that for what purpose the building was used.
(iii) Mackenzie mentioned that it could be a council chamber where king used to attend the meetings with his advisors.
Hazara Ram Temple:
(i) It had a spectacular architeture. It was probably used by the king and his family.
(ii) No idols have been found in this temple while it had sculpted panels on the walls, included the scenes from the Ramayana on the inner walls.

Answer 8:
(i) The first step towards the acquisition of Awadh was the imposition of the Subsidiary Alliance in 1801. To expand British territories in India, governor general Wellesley devised the method of Subsidiary Alliance in 1798.
(ii) Linder the Subsidiary Alliance the native nawab signing the treaty was compelled to accept the following terms.
(a) Permanent stationing of British troops in his territory. Payment of subsidiary for the maintenance of the troops.
(b) Posting of British Resident in his court to act accordance with his advice. He would not employ any European without approval of the British and no negotiation to be done with any other ruler without consulting the Governor General.

Answer 9:
(i) British government gave special focus on mapping as it believed that good maps are very much necessary to understand the landscapes and to know about the topography.
(ii) Whenever towns started to grow then maps were prepared to make plans of development of these towns. Maps were prepared to develop commerce and consolidate the power.
(iii) Maps of the towns provide the information regarding the location of rivers; hills and vegetation. This information is very important for planning structures for the defence utility.
(iv) The maps were also used to show density and quality of houses and alignment of roads; location of ghats and guage the trading possibilities and prepare a plan or strategies for taxation.

Answer 10:
Expected answer.

1.  Both sex are equal
2. No gender biased discrimination.
3. Positive attitude and cooperation.
4. To maintain social honour.

Answer 11:

1. Lord Shiva was worshipped by most of the people during the Harappan civilization.
2. Lord Shiva is still worshipped by crores of people.
3. The people of Harappan culture worshiped mother goddess. In modem time, the mother goddess is worshiped all over India with devotion and dedication.
4. Many people find the abode of gods and goddesses in peepal and other trees.
5. The people of the Harappan age worshipped ox and other animals. These days all such animals are known as the carriers of various gods and goddesses.
6. The worship of Shivalingam is prevalent in the Hindu religion.
7. The people of Harappan civilisation considered water as pious and sacred. They used to take bath in the ‘Great Bath’ on religions occasions.
8. Such glory and piety of the water still exists at prominent places where people take bath on different religious occasions.

Answer 12:

1.  Al-Biruni has described the caste system in India. He mentioned similar systems in other societies of the world.
2. There were four social categories in ancient Persia.
   (a) Knight and Princes
   (b) Monks – fire priests and lawyers
   (c) Scientists, Astronomers and physicians
   (d) Peasants and Artisans
3. Al Biruni accepted the Brahmanical description of the caste system but he did not accept its notion of pollution. According to him, that is impure attempts to regain its original condition of purity. The sun cleans the air. He considered the notion of social pollution as contrary to the laws of nature.
4. The system of four vamas: A1 Biruni gave an account of the system of vamas of Indian society.
   (a) Brahmans: They belonged to the highest caste, as they were created from the head of Brahma. The Hindus consider them superb of mankind.
   (b) Kshatriyas: The were the important part of the society but below the Brahmans. They were created from the shoulders and hands of Brahma.
   (c) Vasishyas: They were ranked at the third position as the were created from the thigh of Brahma.
   (d) Shudras: They were at bottom of the social hierarchy. They were created from the feet of Brahma. No big difference was there between the vaishyas and shudras.
5. ‘Al-Biruni’s description of the caste system was deeply influenced by his study of normative Sanskrit books.
6.  The caste system was based on the rules framed by the Brahmans but in real life this system was not very rigid.

OR

1. Abul Fazl wrote Ain-i-Akbari in 1598. It was a part of the project of writing of history under the order of Akbar. It is also called as Akbar Nama. It is a compendiun of imperial regulations.
2. Akbar Nama is gazette of the Mughal empire. It gave detailed information about the different aspects of life during the Mughal regime.
3. It is a comprehensive analysis of the court, administration and army. It depicts the literary, cultural and religious traditions of the people.
4. Akbar-Nama gives a physical layout of the provinces of Akbar’s empire and enumerates the sources of the revenue.
5. It mentions about the different custom and practices of the Mughal period. It also explains short biographical sketches of imperial officials such as mansabdars.
6. The book was to facilitate emperor Akbar in the governance of its empire, not a reproduction of official papers.
7. Ain – i – Akbari was an authentic attempt to present quantitative data at one place basically.
8.  It was an outstanding testimonial of its times. It provides a fascinating look into the glimpses of the structure and organisation of the Mughal empire.

Answer 13:

1. Mahatma Gandhi attained a supreme place in history of the modem India. Under his leadership the national movement got such a way which led directly to independence of India in 1947. His weapons were truth and non-violence. He forced the British to quit India.
2. His political life was begun in South Africa. He came back from England and started his pratice as lawyer in India.
3. When Gandhiji reached South Africa he observed that the condition of Indians was pitiable. The white government of South Africa maltreated them.
4. Gandhiji could not tolerate their insult so he started his satyagraha against the white government of South Africa. He helped the people in getting their rights.
5. Gandhiji came to India from South Africa in 1916. The British government was fighting the World War I against the Axis powers. British needed both men and money. Then he appealed to the people to cooperate with them.
6. Gandhiji’s strategy was to win the hearts of the British by helping them as he was convinced that the British would set free India after the end of war.
7. First World War ended but the British did not do anything to make free India. Contrary to the expectations of the people, they passed the Rowlatt Act.
8. Gandhiji was upset to see this drastic law. He decided to start non-cooperation movement against the British Rule in 1920. It was called off as violence took place at Chauri Chaura in Uttar Pradesh. Many other movements were also led by him to make India free from the British.

OR

1. The Hindu landlords, Mahajans and middle class professionals had started to threaten anti Muslim feelings after 1870.
2. They instigated people by reminding them the absolutism of Muslim rulers and their atrocities on people dining the medieval age.
3.  They considered the issue of Hindi in the United Province and Bihar. They gave it a communal color.
4.  They propagated that Urdu was the language of the Muslims and Hindu was the language of the Hindus.
5. Many campaigns were organised against the cowslaughter all over the country after 1890. They were against the Muslims not against the British.
6.  The British military cantonments were left open for the cow-slaughter.
7.  In Punjab, the Hindu Sabha was established. In 1909, it critisised Congress saying that the latter wanted to unite all the communities.
8.  It opposed the anti-imperialist policies of Congress. It waged a war against the Muslims and wanted to appease the British.

Answer 14:
(i) (a) Empire was divided into districts and district consisted of a number of villages.
(b) District head was known as Sthanika, and village headman was called gramika.
(c) The king had supreme powers. A council of ministers or mantri parishad, advised the king.

(ii) (a) Some of the officers measured the land and collected taxes.
(b) Some were the incharge of huntsmen who were entrusted with the power of rewarding of punishing them as required.

(iii) (a) Literary sources like Chanakya’s ‘Arthashastra’ and Megasthanes’ Indica.
(b) Buddhist, Jaina, Puranic literature and Sanskrit literary works like the Mudrarakshasa.

Answer 15:
(i) (a) Most important item of import was horses.
(b) War was dependent on an efficient cavalry’.

(ii) (a) Revenue derived from trade contributed significantly to the prosperity of the state.
(b) Trade was considered as a status symbol. Wealthy population demanded high value exotic goods, mainly precious stones and jewellery.

(iii) (a) Importance of harbours
(b) Foreign sailors were suitably looked after.
(c) Encoraging traders to settle and indulge in trade activities.

Answer 16:
(i) (a) The ‘Sahukars’ were attacked. Bahi khatas were burnt and debt bonds which were legally enforceable destroyed.
(b) Terrified of peasant attacks, the Sahukars fled from the village left their property and other belongings behind.

(ii) (a) Police posts were established in village to frighten the rebellious peasants.
(b) Troops were mobilised quickly and 951 people were arrested.

(iii) (a) The revenue demand was high and subject to revision as per government will.
(b) In the presence of the resentment, anger and fury, perception of injustice and suffering, historian got a glimpse of the life of rebels.
(c) Revolts produced records; actions of state to repress them; enquiry into its causes and remedial policies to formulate peace.

Answer 17:

(2) (A) Ahmedabad (B) Amritsar (C) Champaran

We hope the CBSE Sample Papers for Class 12 History Paper 7 help you. If you have any query regarding CBSE Sample Papers for Class 12 History Paper 7, drop a comment below and we will get back to you at the earliest.

These Sample papers are part of CBSE Sample Papers for Class 12 History Here we have given CBSE Sample Papers for Class 12 History Paper 6.

CBSE Sample Papers for Class 12 History Paper 6

Board	CBSE
Class	XII
Subject	History
Sample Paper Set	Paper 6
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 6 of Solved CBSE Sample Paper for Class 12 History is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 80

General Instructions

(i) Answer all the questions. Some questions have internal choice. Marks are indicated against each question.
(ii) Answer to question nos l to 3 carrying 2 marks should not exceed 30 words each.
(iii) Answer to question nos. 4 to 9 carrying 4 marks should not exceed 100 words. Students should attempt only 5 questions in this section.
(iv) Question 10 (for 4 marks) is a value based question and compulsory question.
(v) Answer to question nos 11to 13 carrying 8 marks should not exceed 350 words.
(vi) Questions 14 -16 are source based questions and have no internal choice.
(vii) Question 17 is a map question includes ‘identification’ and significant’ test items.

PART-A

Answer all the questions given below:

Question 1:
Who wrote Harshacharita? What is it about?

Question 2:
Who was Basavanna? Which Bhakti movement did he lead?

Question 3:
What was the significance of the Congress annual session at Lahore in Dec. 1929?

PART-B
Section-I

Answer any five of the following questions:

Question 4:
What were found in burials at the Harappan sites? Discuss.

Question 5:
In what way the begums of Bhopal helped in preserving the Stupa at Sanchi?

Question 6:
Discuss the major teachings of Guru Nanak Dev.

Question 7:
Discuss the distinctive features of the Vitthala Temple.

Question 8:
Explain the religious causes for the mutiny of 1857.

Question 9:
“India is a sovereign, socialist, secular, democratic republic” How? Explain.

Section-II

Value Based Question

Question 10:
Read the following passage and answer the question that follow:

The Constituent Assembly finally recommended that untouchability be abolished. Hindu temples be thrown open to all castes, and seats in legislature and jobs in government offices be reserved for the lowest castes.
Untouchability was a social evil which was abolished by the Constituent Assembly. Which values were to be expected to develop among the people of the different caste groups?

PART-C

Answer all the questions given below:

Question 11:
What is vama system? Explain the ideal occupations for each vama.
OR
Discuss the causes for the development of a new belief of Mahayana in Buddhism.

Question 12:
Discuss the unique system of communication in India which amazed Ibn Battuta with special reference to the postal system.
OR
What were the collective features of the Mughal nobility?

Question 13:
Discuss the impacts of American civil war of 1861 on Indian peasants.
OR
Examine the conditions of women in the social changes that took place in the cities during the 19^th century.

Part-D

Source Based Question

Question 14:
Read the following excerpt carefully and answer the questions that follow:

The Malabar Coast

Here is an excerpt from Periplus of the Erythraean Sea, composed by an anonymous Greek sailor (c. first century CE): They (i.e. traders from abroad) send large ships to these market – towns on account of the great quantity and bulk of pepper and malabathrum (possibly cinnamon, produced in these regions). These are imported here, in the first place, a great quantity of coin; topaz …antimony (a mineral used as a colouring substance), coral, crude glass, copper, tin, lead… There is exported pepper, which is produced in quantity in only one region near these markets … Besides this there are exported great quantities of fine pearls, ivory, silk cloth,… transparent stones of all kinds, diamonds and sapphires, and tortoise shell. Archaeological evidence of a bead-making industry, using precious and semi-precious stones, has been found in Kodumanal (Tamil Nadu). It is likely that local traders brought the stones mentioned in the Periplus from sites such as these to the coastal ports.

1. How did the exchange of goods take place?
2.  Mention the working of the bead making industry.
3.  Write the importance of the Malabar coast.

Question 15:
Read the following excerpt carefully and answer the questions that follow:

Cash or Kind?

The Ain on land revenue collection: Let him (the amil – guzar) not make it a practice of taking only in cash but also in kind. The latter is effected in several ways. First, kankut: in the Hindi language kan signifies grain, and kut, estimates … If any doubts arise, the crops should be cut and estimated in three lots, the good, the middling, and the inferior, and the hesitation removed. Often, too, the land taken by appraisement, gives a sufficiently accurate return. Secondly, batai, also called bhaoli, the crops are reaped and stacked and divided by agreement in the presence of the parties. But in this case several intelligent inspectors are required; otherwise, the evil- minded and false are given to deception. Thirdly, khet-batai, when they divide the fields after they are sown. Fourthly, lang batai, after cutting the grain, they form it in heaps and divide it among themselves, and each takes his share home and turns it to profit.

1.  What was Kankut?
2.  Which of the four methods of revenue collection was best suited for the farmer?
3.  Name the four methods of assessing the land revenue.

Question 16:
Read the following excerpt carefully and answer the questions that follow:

I believe sparate electorates will be suicidal to minorities

During the debate on 27 August 1947, Govind Ballabh Pant said: I believe separate electorates will be suicidal to the minorities and will do them tremendous harm. If they are isolated for ever, they can never convert themselves into a majority and the feeling of frustration will cripple them even from the very beginning. What is it that you desire and what is our ultimate objective? Do the minorities always want to remain as minorities or do they ever expect to form an integral part of a great nation and as such to guide and control its destinies? If they do, can they ever achieve that aspiration and that ideal if they are isolated from the rest of the community? I think it would be extremely dangerous for them if they were segregated from the rest of the community and kept aloof in an air-tight compartment where they would have to rely on others even for the air they breathe… The minorities if they are returned by separate electorates can never have any effective voice.

1. What are separate electorates?
2. Why were some Muslims like Begum Aizaz Rasul against it?
3. Why did G.B Pant felt separate electorates would be suicidal for the minorities? When did he say so?

Question 17:
(17.1) On the given outline map of India locate and label the following with appropriate symbols:
(a) Surat: (city under British control 1857)
(b) Jhansi: (centre of the revolt)

(17.2). On the same outline map of India, three centres related to mature Harappan sites have been marked as A, B, and C. Identify them and write their correct names on the lines drawn after them.

Answers

Answer 1:
(i) Banabhatta wrote Harshacharita.
(ii) Harshacharita is a biography of Harshvardhana, who was the ruler of Kannauj Banabhatta composed it in Sanskrit.

Answer 2:
(i) Basavanna was a brahmana. He was initially a jaina and minister in the court of Chalukya king.
(ii) His followers were known as Virashaivas, the heros of Shiva.

Answer 3:
(i) The election of Jawaharlal Nehru as President.
(ii) The proclamation of commitment to ‘Puma Swaraj’.

Answer 4:
(i) Jewellery has been traced in burials of both men and women. There are several instances where dead were buried with copper mirrors.
(ii) Some graves at Harappa had pottery and ornaments. These objects indicated a belief that these could be used in the after life.
(iii) Throughout the length and breadth of the Harappan settlement the archaeologists have found querns, pottery, needles, flesh, rubbers etc.
(iv) In the excavations at the cemetery in Harappan an ornament consisting of three shell rings, a jasper bead and hundreds of micro beads were found near the skull of a male.

Answer 5:
(i) Shahjahan Begum and her successor Sultan Jahan Begum of Bhopal were the rulers of Bhopal. They made generous grants to the preservation of the Stupa of Sanchi.
(ii) A museum was built nearby the stupa and it was built on the financial aid of Begum Sultan Jahan Begum.
(iii) Some support to preserve the stupa received from the Europeans.
(iv) French and British both took the plaster cast copies of the pillars of the stupas to be displayed in the museums at France and Britain. They contributed financially to preserve the stupa.

Answer 6:
(i) Guru Nanak Dev insisted that his followers should live in their houses and should try to attain salvation by giving them duty in a proper way.
(ii) He opposed the caste system prevalent in the society and gave the message that all caste based comparisons are baseless as we all are the same.
(iii) Guru Nanak Dev asked his followers to adopt productive and useful occupations and expected to contribute to the general funds of community welfare.
(iv) He opposed idol worship and gave the message that god is omnipresent. Worshipping him in the form of idol is baseless. Further he emphasised that the differences of caste, creed and gender are of no use to attain salvation.

Answer 7:
(i) The Vitthala Temple is in Hampi, constructed by Krishnadeva Raya in 1513. Construction work was started by Krishnadeva Raya, but it also continued after his death. It is dedicated to Vitthala or the Vishnu.
(ii) This temple is constructed in a compound measuring 152 x 94 meters and has three beautiful Gopurams.
(iii) There are 48 magnificent pillars in Kalyana Mandapa that have been carved out of rocks.
(iv) The artistic work on the pillar is very beautiful. A chariot built in the front of the temple add to the beauty of the temple.

Answer 8:
(i) People during the Company rule felt that their religious sentiments are systematically hurt by the government. For them it was an attack on their religious freedom, and an insult.
(ii) Immediate cause: The soldiers were given cartridge greased with cow and pig fat. This causes angry among the Muslims and Hindus alike.
(iii) Reforms by company: The company introduced many religious and social reforms. Many Indians began to believe that it was an attempt on the part the government deviate them from their own religions.
(iv) Activities of Christian Missionaries: Christian missionaries started their work in India. Many of them were involved in spread of education, local people looked upon them with suspicion.

Answer 9:
(i) The constitution of India lays down certain basic features which can not be changed or modified by legitimate authority of India.
(ii) The constitution declares India to be sovereign, socialist, secular, democratic republic. India is sovereign, as it is independent of any foreign control.
(iii) It is socialist as it aims at social and economic equality. It is secular as there is no state religion of India.
(iv) It is democratic as the government is elected by the people directly after every five years. It is a republic because the head of the state is also elected for fixed term of five years by the elected representatives.

Answer 10:
Expected values:

1. Cooperation and coordination
2. Fraternity and equality.
3. Social Harmony
4. Unity in diversity.

Answer 11:

1. According to the vama system society was divided into four vamas. They were the Brahman, the Kshatriya, the Vaishya and the Shudra.
2.  The place of the each vama was fixed in the society on the basis of the birth.
3. Ideal occupation: The ideal occupation for each vama was prescribed in the Dharamasutras.
4. The Brahamans occupied the highest rank in the society. They taught Vedas and performed sacrifices.
5. The Kshatriyas were engaged in warfare and their main function was to protect their people.
6. In the Vama system, the Vaishya were engaged in trade, agriculture and other activities.
7. The fourth and last vama was Shudra. They served the three higher Vamas.
8. The people of each vama in the society followed the set instructions and no one violated the social norms.

OR

1. By the first century CE, there is evidence of changes in Buddhist ideas and practices. Buddhist teachings had given great importance to self effort in achieving nibbna (nirvana).
2. Buddha was regarded as human being who attained enlightenment or nibbna through his own efforts.
3. The idea of a saviour emerged gradually. It was believed that he was one who could ensure salvation.
4. The concept of Bodhisatva also developed who were perceived as deeply compassionate beings who accumulated merit through their efforts.
5. These were not used to attain nibbana and thereby abandon the world, but to help others, (vz’) The worship of images of the Buddha and Bodhisatvas became an important part of their tradition.
6. The new way of thinking was called Mahayana. It was literally known as ‘The Great Vehicle.’
7. Followers of Mahayana regarded other Buddhist as Hinayana.

Answer 12:

1. Due to the efficiency of the postal system Ibn Battuta was amazed, that allowed merchants to not only send information and remit credit across long distances but also to dispatch goods required at short notice.
2. The postal system was so efficient that while it took fifty days to reach Delhi from Sind, the news reports of spies would reach Sultan through postal system in just five days,
3.  According to Ibn Battuta, in India, postal system was of two types:
   (a) The horse post called Ulug it was run by royal horses stationed at a distance of every four miles.
   (b) The foot post has three stations per mile called ‘dawa’-one third of a mile.
4. At every third of a mile there was a well populated village, outside which were three pavilions in which sat men with girded loins ready to start. Each of them carried a rod two cubit in length, with copper belt at the top.
5. The courier get started from the city, holding the letter in one hand and the rod with its bells in the other, and he ran as fast as he could.
6. On hearing the ringing of the bell the man at the other pavilion got ready and took the letter from his hands and ran at the top speed shaking the rod till he reached the next dawa.
7. The process continued till the latter reached at the ultimate station destination.
8.  This way the foot post was quicker than the horse post, and often it was used to transport the fruits of Khurasom which were much desired in India.

OR

1. The corps of officers was one of the most important pillars of the Mughal state. It was referred by historians collectivity as the nobility.
2. The nobility was recruited from diverse ethnic and religious groups. It ensured that no factors were enough to make challenge the authority of the state.
3. These corps of the Mughals were described as a bouquet of flowers held together by loyalty of the emperor. Turani and Iranian nobles were the earliest in Akbar’s imperial service. Many had accompanied Humayun and others migrated later to the Mughal’s court.
4.  From 1560 onwards two ruling groups of Indian origin entered the imperial service-the Rajputs and Indian Muslims. Raj Balrmal Kachhwaha of Amber, was a Rajput chief who joined first as his daughter got married to Akbar.
5. Iranians joined high offices under Jahangir as his politically influential Queen Nur Jahan was an Iranian.
6. Aurangzeb appointed Rajputs to high positions and under him the Marathas accounted for a sizeable number within the body of officers.
7.  All holders of the government offices hold rank or mansabs having designation ‘Zat’. It was the indication of position in the imperial hierarchy and the salary of the Mansabdar.
8. The second one was of sawar, indicating the number of horsemen. He was required to maintain in service. The nobles participated in military campaign and also served as officers of the empire in provinces.

Answer 13:

1.   American Civil War that began in 1860 had a huge impact on the ryots of Deccan region in India.
2. Britain was the country where large cotton mills were operational. These cotton mills depended on cotton imported from North America.
3. During the Civil War it was not possible to import cotton from there (America).
4. The cotton mills were compelled to look forward towards alternative suppliers of cotton apart from the United State of America, India made a good option.
5. The peasants in Deccan were encouraged to grow more cotton. Access to credit was an easy way. The sahukars would give credit of ₹100 for every acre of land under cotton cultivation.
6. The farmers benefited out of this demand for cotton. The real beneficiary were the big farmers and traders.
7. Things changed as normalcy returned to U.S.A. Now the demand for cotton in India declined. The easy availability of credit also declined.
8. The ryots fell back to old days of penury and rose in rebellion in many places.

OR

1. Though the social changes did not happen with ease, but in cities new opportunities for women were offered.
2. Middle class women sought to express themselves through the medium of journals, autobiographies and books.
3. Many people resented the attempts to change traditional patriarchal norms.
4. Conservatives feared that the education of women would turn the world upside down and threaten the basis of the entire social order.
5. Reformers who supported women’s education saw women primarily as mothers and wives and made them to remain within the enclosed spaces of the household.
6. Over time women became more visible in public, as they entered new professions in the city as domestic and factory workers, teachers and theatre and film actresses.
7. But for a long time women who moved out of the household into public space remained the objects of social censure.

Answer 14:
(i) (a) Exchange of goods were facilitated by introduction of coinage. Coins were issued not only by rulers but symbols on punch-marked coin indicate it is likely merchants, bankers too issued them etc.
(b) Topaz, glass, copper, tin were probably imported and in demand. Spices, tortoise shell were exported in exchange.

(ii) (a) The bead making industry found at Kodumahal, used precious and semi-precious stones found in the region.
(b) The local traders bought the stones from the sites to the coastal ports for exchange
and trade with traders from abroad.

(iii) (a) Malabar coast was an important link in India’s trade imports and exports.
(b) From 6th century BCE the ports that dotted the west coast connected India overseas.
(c) The ports connected the sub continent across the Arabian sea in East and North Africa and West Asia.

Answer 15:
(i) (a) It was the land revenue system prevalent during Mughal period in India.
(b) It is made of two words ‘Kan’ and ‘Kut’, meaning, the grain and estimate respectively. It means the estimate of grain.

(ii) (a) The long batai system was the most fair because the crop was divided after cutting of the grain.
(b) The dues were computed there and then, to the advantage of both the state and the peasants. This system left no scope for either the state or peasants being in any doubt as in the case of Kankut or khet batai.
(c) The only essential requirement was an army of honest officials to be present at the time of division.

(iii) (a) Kankut
(b) Batai (bhaoli)
(c) Khet – batai
(d) Long batai

Answer 16:
(i) Separate electorates meant that in certain constituencies seats were reserved only for the members of a particular community or religion.

(ii) (a) Begum Aizaz Rasul felt that separate electorates were self destructive.
(b) They isolated the minorities from the majority.

(iii) (a) G.B. Pant felt separate electorates were suicidal because it would permanently isolate and segregate the minorities.
(b) They make them vulnerable and deprive them of an effective say within the government.
(c) He said this on 27 August 1947 during the debate.

Answer 17:

(2) (A) Nageshwar (B) Kot Diji (C) Mohenjodaro

We hope the CBSE Sample Papers for Class 12 History Paper 6 help you. If you have any query regarding CBSE Sample Papers for Class 12 History Paper 6, drop a comment below and we will get back to you at the earliest.

These Sample papers are part of CBSE Sample Papers for Class 12 History Here we have given CBSE Sample Papers for Class 12 History Paper 5.

CBSE Sample Papers for Class 12 History Paper 5

Board	CBSE
Class	XII
Subject	History
Sample Paper Set	Paper 5
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 5 of Solved CBSE Sample Paper for Class 12 History is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 80

General Instructions

(i) Answer all the questions. Some questions have internal choice. Marks are indicated against each question.
(ii) Answer to question nos 1 to 3 carrying 2 marks should not exceed 30 words each.
(iii) Answer to question nos. 4 to 9 carrying 4 marks should not exceed 100 words. Students should attempt only 5 questions in this section.
(iv) Question 10 (for 4 marks) is a value based question and compulsory question.
(v) Answer to question nos 11 to 13 carrying 8 marks should not exceed 350 words.
(vi) Questions 14 -16 are source based questions and have no internal choice.
(vii) Question 17 is a map question includes ‘identification’ and significant test items.

PART-A

Answer all the questions given below:

Question 1:
Mention two important characteristics of the Harappan script.

Question 2:
Whose books did Al-Biruni translate into Arabic and Sanskrit?

Question 3:
State two features of Ricardian ideas.

PART-B
Section-I

Answer any five of the following questions:

Question 4:
What means were used by Asoka to maintain control over the diverse empire?

Question 5:
Who were regarded as beyond the four vamas?

Question 6:
Why is Ibn Batuta known as globe trotter? Discuss.

Question 7:
Discuss the responsible factors for the decline of the Vijayanagara Empire.

Question 8:
What steps did the British take to quell the uprising?

Question 9:
What was the role of introduction of railway in 1853 in the process of urbanisation?

Section-II

Value Based Question

Question 10:
Read the following passage and answer the question that follow.

“Mahabharata describes a feud over land and power between two groups of cousins, the Kauravas and the Pandavas who belonged to a single ruling family, that of the Kurus, a lineage dominating one of the janapadas. Ultimately, the conflict ended in a battle in which the Pandavas emerged victorious. Many conflicts and wars took place in the history of the world with different purposes. The Mahabharta, a furious battle took place between two groups of cousins over land and power. Mention the values by which the battle could be stopped or ignored.

PART-C

Answer all the questions given below.

Question 11:
Evaluate the trade relations of the Harappans with West Asia.
OR
Why did Amaravati stupa not survive?

Question 12:
Mention the similarities between sufism and bhakti movements.
OR
How was the ideal of Sulh-i-kul implemented?

Question 13:
Why did the colonial rulers develop hill stations? Explain.
OR
Elaborate the causes that led to the non-cooperation movement.

PART-D

Source Based Questions

Question 14:
Read the following excerpt carefully and answer the questions that follow.

In Praise of Samudragupta

This is an excerpt from the Prayaga Prashasti: He was without an antagonist on earth; he, by the overflowing of the multitude of (his) many good qualities adorned by hundreds of good actions, has wiped off the fame of other kings with the soles of (his) feet; (he is) Purusha (the Supreme Being), being the cause of the prosperity of the good and the destruction of the bad (he is) incomprehensible; (he is) one whose tender heart can be captured only by devotion and humility; (he is) possessed of compassion; (he is) the giver of many hundred-thousands of cows; (his) mind has received ceremonial initiation for the uplift of the miserable, the poor, the forlorn and the suffering; (he is) resplendent and embodied kindness to mankind; (he is) equal to (the gods) Kubera (the god of wealth), Varuna (the god of the ocean), Indra (the god * of rains) and Yama (the god of death)…

1.  What is a Prashasti? Who wrote the above Prashasti?
2.  Why did rulers identify themselves with a variety of deities?
3. Mention the sources for studying about the Guptas.

Question 15:
Read the following excerpt carefully and answer the questions that follow.

Declining a royal gift

This excerpt from a sufi text describes the proceedings at Shaikh Nizamuddin Auliya’s hospice in 1313:1 (the author, Amir Hasan Sijzi) had the good fortune of kissing his (Shaikh Nizamuddin Auliya’s) feet… At this time a local ruler had sent him the deed of ownership to two gardens and much land, along with the provisions and tools for their maintenance. The ruler had also made it clear that he was relinquishing all his rights to both the gardens and land. The master … had not accepted that gift. Instead, he had lamented: “What have I to do with gardens and fields and lands? … None of… our spiritual masters had engaged in such activity.” Then he told an appropriate story: “… Sultan Ghiyasuddin, who at that time was still known as Ulugh Khan, came to visit Shaikh Fariduddin (and) offered some money and ownership deeds for four villages to the Shaikh, the money being for the benefit of the dervishes (sufis), and the land for his use. Smiling, Shaikh al Islam (Fariduddin) said: ‘Give me the money. I will dispense it to the dervishes. But as for those land deeds, keep them. There are many who long for them. Give them away to such persons.’”

1.  What does it reflect about sufi traditions?
2.  Mention two contributions of Sufism.
3.  Where is Sheikh Nizamuddin’s dargah located and which order did he belong to? What is Silsila?

Question 16:
Read the following excerpt carefully and answer the questions that follow.

A ryot petition

This is an example of a petition from a ryot of the village of Mirajgaon. Taluka Kaijat, to the Collector, Ahmednagar, Deccan Riots Commission:
The sowkars (sahukars)… have of late begun to oppress us. As we cannot earn enough to defray our household expenses, we are actually forced to beg of them to provide us with money, clothes and grain, which we obtain from them not without great difficulty, nor without their compelling us to enter into hard conditions in the bond. Moreover the necessary clothes and grain are not sold to us at cash rates. The prices asked from us are generally twenty-five or fifty per cent more than demanded from customers making ready money payments… The produce of our fields is also taken by the sowkars, who at the time of removing it assure us that it will be credited to our account, but they do not actually make any mention of it in the accounts. They also refuse to pass us any receipts for the produce so removed by them.

1. Why were the ryots not given loans by ‘Sahukars’?
2.  Mention the difficulties the ryots had to face for getting loans from the Sahukars.
3. Why were the ryots unable to pay the inflated demand?

PART-E

Question 17:
Map Question.
17.1 On the given outline map of India, locate and label the following with appropriate symbols
(a) Mathura (b) Ujjain

17.2 On the same outline map of India three centres related to the main centres of Indian
National Movement have been marked as A, B and C. Identify them and write their correct names on the lines drawn near them.

Answers

Answer 1:
(i) It was not alphabetical but pictographic (had between 375 and 400 signs) script was written from left to right.
(ii) Despite constant efforts has not been deciphered to date.

Answer 2:
(i) Al-Biruni translated Patanjali’s work on Sanskrit Grammar into Arabic.
(ii) He also translated Euclids (a greek Mathematicians book) into Sanskrit.

Answer 3:
(i) Landowner had only claim to average rent and state needed to tax the surplus.
(ii) If surplus of landowner was not taxed, landowners were unlikely to invest in improvement of the land, but were likely to turn into rentiers.

Answer 4:
(i) Communication along both land and riverine routes vital for the empire, were well maintained as journey from centre to the provinces could take weeks and were difficult.
(ii) A large standing army was maintained to ensure provisions and protection of those who were on the move.
(iii) Megasthenes mentioned, a committee of 30, with 6 sub-committees of 5 members each, for co-ordinating military activity.
(iv) Asoka set a very high ideal and this was the ideal of paternal kingship. He also tried to hold his empire by propagating dhamma, through special officers known as Dhamma Mahamattas. He abandoned the policy of physical occupation-bherigosha in favour of policy of cultural conquest i.e. dhammaghosha.

Answer 5:
(i) The Brahmanas regarded the social category of untouchables as beyond and outside the system. This notion was based on certain activities performed by people as ‘polluting’ – handling of corpses and dead animals.
(ii) People who performed such tasks, were known as Chandalas. Untouchables are placed at the very bottom of the hierarchy. Their touch and shadow was regarded as polluting.
(iii) The duties of the Chandalas were laid down by the Manusmriti. They were to live outside the village, use discarded utensils and clothes and use only iron ornaments.
(iv) Chandalas were not allowed for walking in villages and cities at night. To know the lives of “Chandalas’ and their attitude to the life of degradation prescribed by Shastras, historians rely on non-Brahmanical texts.

Answer 6:
(i) Ibn Batuta is known as globe trotter because he travelled for 30 years after his setting off from his town Tangier, Morocco. Experience gained through travels are more important and reliable source of knowledge than books.
(ii) His travel itinerary included pilgrimage trips to Mecca, extensive travels in Syria, Iraq, Persia, Yemen, Oman and a few trading ports on the coast of East Africa before he set off for India in 1332-33.
(iii) Ibn Batuta travelled to India through Central Asia reached Sind in 1333, and passing through Multan and Ulch set off for Delhi. Muhammad-bin-Tughlaq appointed him as Qazi of Delhi which he held for many years.
(iv) He proceeded to China in 1342. Before it, he travelled to Malabar coast, Maldives, Sri Lanka, Bengal, Assam, Sumatra. He travelled extensively in China. He came back in 1354. He was compared with Marco Polo.

Answer 7:
(i) After the death of Krishnadeva Raya in 1526, strains began to show within imperial structure. Claimants to power included members of the ruling lineage as well as military commanders. Military nayaks troubled his successors.
(ii) By 1542 control at the centre shifted to the ruling lineage Aravidu that remained in power till the end of the 17th century.
(iii) Sadashiv Ray ascended the throne in 1543 but the real power lay in the hands of a triumvirate in which the leading person was Rama Raja. He tried to play off the various Muslim powers against one another in order to maintain balance of power favourable to Vijayanagara.
(iv) Ahmadnagar, Bijapur, Golconda armies combined to inflict and crushing defeat on the armies of Vijayanagra led by Ram Raja at Talikota.
(v) The battle of Talikota marked the end of the great age of Vijayanagara. All victorious armies sacked the city and the city was eventually abandoned.

Answer 8:
(i) The British had a tough time putting down the uprising. The suppression of the uprising was accomplished by a two prolonged approach of military strategy and the submission ofTalukdars.
(ii) Enactment of a series of Acts in May and June 1857 that empowered them to put North India under martial law and gave officers and even ordinary British, power to try and punish Indians suspected of rebellion.
(iii) Military attack was mounted on Delhi as it had a symbolic value. One force moved from north of Calcutta and other from Punjab. Despite great losses on both sides Delhi was recovered in late September 1857.
(iv) Apart from use of military power on a gigantic scale, the British broke the United resistance of big landholders and peasants by promising to give back big landholders their estates.
(v) Another strategy was rewarding the loyal landholders and taking action against rebel landholders by dispossessing them. Thereby breaking up the unity of the landholders and also the peasants.

Answer 9:
(i) The railway was introduced in 1853 in India. It brought changes in the fortunes of towns.
Centres of economic activities were shifted away from traditional towns as these towns were situated along old routes and rivers.
(ii) Railway stations became the centres of collection of raw material and distribution point for imported goods.
(iii) Mirzapur was the main collection centre of cotton and cotton goods from Deccan, on the bank of the Ganga. This declined when a railway link was started to Bombay.
(iv) Railway workshops and colonies of its employees were established with the expansion of the railway network. Many railway towns such as Waltair, Bareiley etc. were developed.

Answer 10:
Expected Values

1.  Justice
2. Patience
3.  Fraternity and Modesty
4. Self Control and Coordination
5. Selflessness

Answer 11:

1. Harappans had trade relations with West Asia, Oman, Mesopotamia and Afghanistan.
   Many objects of Harappan culture like beads, seals, a monkey on a pin have been recovered in Mesopotamia.
2. Sumerian articles like model ram and small pottery ring have been found in India.
3.  Meluhha and Magan are identified with the Harappan region. Meluhha was referred to land of seafarers.
4.  Mesopotamian texts mention two intermediary trading centres, Dilmun (Today Bahrein) Meluhha and Magan (Oman) where goods were exchanged.
5.  Depictions of ships and boats on seals, scholars state, are indicative of trade relations.
6. Archaeological sources indicate that Harappans brought copper from Oman, chemical analysis show Omani copper and Harappan artefacts have traces of nickel.
7. A large Harappan Jar has been found at Omani sites, the contents of which were exchanged for Omani copper.
8. Mesopotamian texts refer to copper coming from Magan and copper found at Mesopotamian sites also has traces of nickel.

OR

1.  Amravati was discovered as early as 1796, before scholars understood the value of finds and realised how critical it was to preserve finds ‘in situ’.
2.  The local raja who stumbled on the finds used the stone to build a temple. Due to his ignorance he mistook the mound of the stupa to be a sight of buried treasure.
3. Walter Elliot, the Commissioner of Guntur collected several sculptured panels and took them away to Madras. These were called Elliot marbles.
4.  By 1850s some of the slabs of Amravati adorned gardens of British officials, London office, Asiatic Society of Bengal at Calcutta and India office in Madras.
5. New officers plundered the sculptures on the plea that other officials had done the same.
6. Amravati was discovered before Sanchi. It did not survive because it fell prey to the ravages of men, who did not understand the real
   value of the find.
7. They were mere pieces of art, beautiful and worth possessing, unaware of its history, and sanctity.
8.  Today, it stands bereft of its former glory, just as an insignificant mound.

Answer 12:

1.  The important belief in the need to unite with God was common to both as was stress on love as the basis of relationship with God. Each movement gained from the other.
2. They were sternly opposed to prejudice on the basis of caste, religion and divisions.
3. They believed also that the acceptance of a guru or pir at least in the initial stages was necessary.
4. They represented a collective introspection and soul searching by a society causing a metamorphosis in some of its biases and assumptions.
5.  In their stress an egalitarianism and brotherhood and valorisation of devotional love.
6.  They became vehicles for mutual tolerance, understanding and goodwill.
7.  It was apart from spread of regional language, literature, music and Indo-Islamic architecture.

OR

1. The ideal of Sulhi-i-kul was implemented through state policies. Under the Mughals positions and awards were given purely on the basis of service and loyalty to the king.
2. The nobility was a composite one comprising Iranis, Turanis, Afghans, Rajputs and Deccans.
3.  Akbar abolished taxes based on religious discrimination. The tax on pilgrimage was abolished in 1563 and tax on Jizya in 1564.
4. Instructions were sent to officers of the empire to follow the precepts of Sulhi-i-kul in administration.
5. Mughal emperors gave grants to support the building and maintenance of worship places.
6.  As temples were destroyed during war, it was known from the reigns of Shah Jahan and Aurangzeb that Grants were issued for their repair work.
7.  During the reign of Aurangzeb, Jizya was re-imposed on non-Muslim subjects.
8.  The philosophy of Sulh-i-kul attempted to bridge the gap between the divine and temporal authority. The emperor became a representation of the whole universe and a symbol of pure spiritual wisdom.

Answer 13:

1.  The initial reason for founding and settling hill stations was military. They wanted to serve as a new type of cantonments in the hill.
2.  Hill stations became strategic places for billeting troops, guarding frontier and beginning campaigns against enemy rulers. Simla was founded during Gurkha War (1815) and Mount Abu – as a result of Anglo-Maratha War (1818).
3.  The hill stations served as sanatoriums places, where soldiers could recoup from illness and revitalise their energies.
4.  The climate of hill stations approximated the cold climates of Europe. They became more attractive and alternate destinations for the Britishers during summer months.
5. The Viceroy John Lawrence officially moved his council to Simla. It became the summer capital of the British and official residence of the commander-in-chief of the Indian army.
6. The suitable climate enabled the British and other Europeans to recreate settlements that were reminiscent of house-buildings in European style, detached villas, cottages amidst gardens, churches, etc.
7.  Entertainment activities like social calls, teas, picnics, fetes came to be shaped by British cultural traditions. All these symbolised cultural hegemony, racial distinctiveness and superbness.
8.  Hill stations became important adjuncts for the colonial economy as setting up the tea and coffee plantations. The cheap labours from adjoining areas added to the economic feasibility. Railways made these areas more accessible.

OR

1. The Rowlatt Act was passed against the wish of all Indian members of the Legislative Assembly in 1919. It empowered the government to detain a person without trial violating all civil rights.
2. TO make protest against the unlawful arrest of national leaders a public meeting held in Amritsar culminated in what is known as Jallianwala Bagh massacre in April 1919.
3.  Inside the Bagh, British Brigadier General Dyer ordered his troops to open fire on a nationalist meeting without warning. More than 600 innocent people men, women and children were killed and many more injured.
4. The monstrous act provoked unprecedented indignation throughout the country and shocked the conscience of some British also.
5.  The government wanted to terrorise the Indians by this but it failed to curb the aspirations of the people.
6. The khilafat movement was launched by the Ali brothers to protest against the dismemberment of the Turkish empire and to restore the Turkish Sultan as the spiritual head of the Muslims.
7.  Gandhiji clubbed the non-cooperation movement with the khilafat movement to restore unity among the two religious communities, the Hindus and the Muslims.
8. The Act of 1919 failed to satisfy the nationalist urge for the Swaraj. With and by the non-cooperation movement the nationalists wanted to achieve a new scheme of fruitful and substantial reforms.

Answer 14:
(i) (a) Prashastis are inscriptions composed in praise of kings by eminent poets.
(b) It was written by Samudragupta’s court poet Harisena. „

(ii) (a) Rulers claimed divine status because the rulers did not exercise direct control over larger parts of their kingdom.
(b) By adopting high sounding titles and super-human qualities equivalent to gods dwelling on earth they sought to gain legitimacy and exercise authority over their feudatories.
The prashasti equates the ruler to
(a) Kuber-the god of wealth
(b) Indra-the god of rains
(c) Varuna-the God of the Ocean
(d) Yama-the god of death

(iii) (a) Other sources were coins and inscriptions. Some of the most spectacular gold coins were minted by Gupta rulers.
(b) Inscriptions found on stone and copper plates give valuable information about various aspects of Gupta polity and administration.

Answer 15:
(i) (a) Chisti tradition was austerity including distance from worldly power. No absolute isolation from political power as they accepted endowments for hospices – donations in cash and kind.
(b) Donations were accepted for piety, ritual necessities, food and clothes, etc.

(ii) (a) They acted as channels of communication between the ruler and the ruled.
(b) Helped in indigenising Islam. Served as a constant moderating influence on the power of Sultan, with their simple and egalitarian life.

(iii) (a) In Delhi
(b) Chisti order
(c) A chain signifying a continuous link between master and disciple, stretching as an unbroken spiritual genealogy to the Prophet Muhammad.

Answer 16:
(i) (a) Exports of Indian cotton declined and cotton prices declined. Sahukars wanted the ryots first to clear outstanding debts. .
(b) The ‘Sahukars’ did not have the confidence in the peasants ability to repay.

(ii) (a) Money lenders manipulated laws and forged accounts. They violated the limitation
law passed by the British.
(b) Often Sahukars refused to give receipts when loans were repaid, entered fictious figures in the accounts.
(c) By refusing to pay loans to the ryot the ‘sahukars’ was being insensitive and violating the customary norms of the village.

(iii) (a) While credit dried up revenue demand increased.
(b) Sahukars refused loans and peasants were unable to pay the inflated demand.

Answer 17:

(2) (a) Calcutta (b) Lucknow (c) Delhi

We hope the CBSE Sample Papers for Class 12 History Paper 5 help you. If you have any query regarding CBSE Sample Papers for Class 12 History Paper 5, drop a comment below and we will get back to you at the earliest.

These Sample papers are part of CBSE Sample Papers for Class 12 History Here we have given CBSE Sample Papers for Class 12 History Paper 4.

CBSE Sample Papers for Class 12 History Paper 4

Board	CBSE
Class	XII
Subject	History
Sample Paper Set	Paper 4
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 4 of Solved CBSE Sample Paper for Class 12 History is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 80

General Instructions

(i) Answer all the questions. Some questions have internal choice. Marks are indicated against each question.
(ii) Answer to question nos 1 to 3 carrying 2 marks should not exceed 30 words each.
(iii) Answer to question nos. 4 to 9 carrying 4 marks should not exceed 100 words. Students should attempt only 5 questions in this section.
(iv) Question 10 (for 4 marks) is a value based question and compulsory question.
(v) Answer to question nos 11 to 13 carrying 8 marks should not exceed 350 words.
(vi) Questions 14 -16 are source based questions and have no internal choice.
(vii) Question 17 is a map question includes ‘identification’and significant’ test items.

PART-A

Answer all the questions given below:

Question 1:
Explain two features of Harara Ram Temple in the royal centre.

Question 2:
Write two rules of the Gotra system.

Question 3:
Mention the immediate causes of the Revolt of 1857.

PART-B
Section-I

Answer any five of the following questions:

Question 4:
Describe briefly the opinion of the archaeologist about the Harappan society.

Question 5:
Discuss administrative system of Maurya.

Question 6:
Describe the features of the stupa of Sanchi.

Question 7:
Write a brief account of local traditions associated with the Sacred Centre.

Question 8:
Explain the distinctive features of Mughal chronicles.

Question 9:
Why did the Deccan ryots revolt against the moneylenders (Sahukars)?

Section II

Value Based Questions

Question 10:
Read the following passage and answer the question that follow.

Pilgrimage, called ziyarat to tombs of sufi saints is prevalent all over the muslim world. This practice in an occasion for seeking the sufi spiritual grace (barakat). For more than seven centuries people of various creeds, classes and social backgrounds have expressed their ) devotion at the dargahs of the five great Chishti saints. Pilgrimage is an important part of human beings of all religions.
What type of values to be flourished in human kinds by such Pilgrimages?

PART-C

Answer all the questions given below:

Question 11:
Discuss the major beliefs and practices that characterized Sufism.
OR
“The Bhakti and Sufi saints used local languages to express their ideas and become very popular”. Discuss it with examples.

Question 12:
Discuss the programmes and objectives of the non-cooperation movement. What is the importance of the movement?
OR
Describe Gandhi’s march to Dandi.

Question 13:
Explain the economic and social life of the people as represented in the Mahabharata.
OR
‘The Mahabharata is a good source to study social value of ancient times’. How?

PART-D

Source Based Questions

Question 14:
Read the following excerpt carefully and answer the questions that follow.

Rules for monks and nuns

There are some of the rules laid down in the Vinaya Pitaka: When a new felt (blanket/rug) has been made by a bhikkhu, it is to be kept for (at least) six years. If after less than six years he should have another new felt (blanket/rug) made, regardless of whether or not he has disposed of the first, then – unless he has been authorised by the bhikkhus – it is to be forfeited and confessed. In case a bhikkhu arriving at a family residence is presented with cakes or cooked grain meal, he may accept two or three bowlfuls if he so desires. If he should accept more than that, it is to be confessed. Having accepted the two or three bowlfuls and having taken them from there, he is to share them among the bhikkhus. This is the proper course here. Should any bhikkhu, having set out bedding in a lodging belonging to the sangha – or having had it set out – and then on departing neither put it away nor have it put away, or should he go without taking leave, it is to be confessed.

1. Why did men and women join sangha? Give two reasons.
2.  What was the Bodh sangha?
3.  Why were these rules framed?

Question 15:
Read the following excerpt carefully and answer the questions that follow.

The Bazaar

Paes gives a vivid description of the bazaar: Going forward, you have a broad and beautiful street… In this street live many merchants, and there you will find all sorts of rubies, and diamonds, and emeralds, and pearls, and seed-pearls, and cloths, and every other sort of thing there is on earth and that you may wish to buy. Then you have there every evening a fair where they sell many common horses and nags, and also many citrons, and limes, and oranges, and grapes, and every other kind of garden stuff, and wood; you have all in this street. More generally, he described the city as being “the best provided city in the world” with the markets “stocked with provisions such as rice, wheat, grains, India com and a certain amount of barley and beans, moong, pulses and horse-gram” all of which were cheaply and abundantly available. According to Femao Nuniz, the Vijayanagara markets were “overflowing with abundance of fruits, grapes and oranges,

1.  What had Paes written about bazaar?
2. Give two characteristic features of the city of Vijaynagara that mention all foreign accounts.
3.  According to Femao Nuniz, what were the three features of the Bazaar?

Question 16:
Read the following excerpt carefully and answer the questions that follow.

This is what Khushdeva Singh writes about his experience during one of his visits to Karachi in 1949: My friends took me to a room at the airport where we all sat down and talked… (and) had lunch together. I had to travel from Karachi to London… at 2.30 a.m…. At 5.00 p.m. had given me so generously of their time, I thought it would be too much for them to wait the ..whole night and suggested they must spare themselves the trouble. But nobody left until it was dinner time… Then they said they were leaving and that I must have a little rest before emplaning…. I got up at about 1.45 a.m. and, when I opened the door, I saw that all of them were still there … They all accompanied me to the plane, and, before parting, presented me with a small basket of grapes. I had no words to express my gratitude for the overwhelming affection with which I was treated and the happiness this stopover had given me.

1. What do you know about Khushdeva Singh?
2.  How did oral history help the historians to reconstruct the events of the recent past?
3.  How did his friends treat him?

Question 17:
(17.1) On the given outline map of India, locate and label the following with appropriate symbol.
(a) Mohenjodaro
(b) Dholavira
(17.2) On the same outline map of India three centres related to the Buddhist sites have been marked as A, B and C. Identify them and write their correct names on the line drawn near them.

Answers

Answer 1:
(i) This was probably meant to be used only by the king and his family.
(ii) The images in the central shrine are missing. However sculpted panel on the wall survive. These include scenes from the Ramayana sculpted on the inner walls of shrine.

Answer 2:
(i) Each gotra Brahmanical practice was named a vedic Seer. All those who belonged to the same gotra were regarded as his descendants.
(ii) Women were expected to give up their father’s gotra on marriage and members of the same gotra could not marry.

Answer 3:
(i) Rumours and prophesies played a part on moving people to action.
(ii) The issue of greased cartridges provided the immediate cause to the culmination of popular discontent with British policies and imperialist exploitation.

Answer 4:
(i) Found Evidence of Agricultural technology and tried to identify the tools used for harvesting.
(ii) They discovered the most unique feature of Harappan and Mohenjodaro sites’ civilization.
(iii) Found whether there was social or economic difference amongst people living within a particular culture.
(iv) They tried to find out about the craft production and make strategies for procuring materials.

Answer 5:
(i) On the basis of fragments of Megasthenes book “Indica”, the Arthashastra of Kautilya, and Asokan inscriptions we can draw the picture of Mauryan system of administration.
(ii) The Mauryas as contrasted with earlier smaller kingdoms, ruled over a empire and organized a very elaborate system of administration.
(iii) At the centre of the structure was king, who had the power to enact laws. The chief function of the king was to maintain social order.
(iv) According to Megasthenes there was a council of ministers or mantri parishad to advise the king but the power of the council seem to be limited and not binding.
(v) The highest functionaries were minister (mantrins), high priest (purohita), commander in chief (senapati) and crown prince (yuvraj).
(vi) Two keys offices in the central administration were of treasurer, responsible for the storage of the royal treasure and of the state income and the chief collector responsible for the collection of revenue from various parts of kingdom.

Answer 6:
(i) The sanchi stupa was built in the 3rd century BCE by Asoka, the great Mauryan king.
(ii) It is a semi circular dome-like structure. The gateways at four cardinal points are its most distinctive feature.
(iii) Each gateways has two square pillars connected by three horizontal and slightly curved parallel stone pillars.
(iv) Beautiful carved capitals are placed above the pillar and below the horizontal base.
(vi) The gateways contain lovely, beautifully carved panels depicting events from the life of Buddha and details from jataka stories.

Answer 7:
(i) The Sacred Centre as per archaeologists and scholars was at the rocky northern end of city on the banks of the Tungabhadra.
(ii) These hills sheltered the Monkey Kingdom of Bali and Sugriva mentioned in the Ramayana.
(iii) Other traditions suggest that Pampadevi, the local mother goddess, did penance in these hills in order to marry Virupaksha, the guardian diety of the kingdom, also recognised as form of Shiva.
(iv) This area is associated with several sacred traditions, as among these hills are found Jaina temples of pre-Vijaynagara period as well.
(v) Temple building in this region had a long history going back to dynasties such as the Pallava, Chalukyas, Hoyasalas and Cholas.

Answer 8:
Historical literature commissioned by Mughal kings, written by court historians have been termed chronicles by historians. The distinctive features of Mughal chronicles are:

1. Akbar-Nama is considered a landmark in the historiographical tradition as it evolved a new style of writing that was ornate and which attached importance to diction and rythm as texts were often read aloud.
2. The Akbar Nama is divided into 3 books of which 2 are chronicles. The third book is Ain-i-Akbari. The Ist volume contains the history of mankind from Adam, to one celestial cycle of Akbar’s life, beginning with the birth of Akbar.
3.  It presents Akbar’s reign as the pinnacle of human history, the milestone of human progress.
   The 2nd volume closes at 46 regional (1601) year of Akbar.
4. The chronicle apart from serving as continuous chronological record of events are a repository of factual information about institution of Mughal state and provide unique insight into the political, geographical administrative, social, ideological, cultural events of the time, e.g. Akbar Nama.
5. Abul Fazal’s writing are a result of careful and exhaustive historical investigations and based on primary documents.

Answer 9:
(i) In rural India, it was traditional rule that the interest will always remain less than the principal amount. However, in some cases interest payable was more than the principal itself. In one case the interest was ? 2000 against principal amount of Rs 100.
(ii) No receipt was paid in case of payment of loan partly or fully. This opened the scope of manipulation by the money lenders.
(iii) Ryots complained about forging of documents and other fraudulent activity by the money lenders.
(iv) Ryots believed that money lenders were insensitive to them and made an arrogant and exploitative lot.

Answer 10:
Expected values:

1.  Self reliance
2. Peace
3.  feeling of co-existence
4. communal harmony

Answer 11:

1. After the advent of Islam in the early middle ages, it saw a new movement in later part.
   The movement has had great impact and reach in the Indian subcontinent. It is called Sufi movement. The sufi saints were mystics. Their preachings included:
2.  Sufi saints did not subscribe to the theological and rigid interpretations of religious scriptures of Islam. They believed that the interpretation have to be based on individual experiences.
3. This way the theological interpretations became flexible. Further the control of the orthodox religious leaders got weakened. This was a people centric move.
4. They rejected the high sounding rituals. They also emphasized on simplicity in religious traditions and rites.
5. Sufi saints prescribed devotion to almighty as path to salvation. They even approved of singing and dancing as part of devotion.
6.  It is notable that classical Islam has forbidden singing dancing and any music.
7. The most important theme of sufi philosophy was that serving people is the true religion. With the objective of serving the poor people they also held langar.
8. Today also one can go to Ajmer and can partake in the langar organised on the tomb of Nizammudin Auliya, the great Sufi saint.

OR

1. The Alvars and the Nayanars who head the Bhakti movement in Tamil region preached their message in Tamil.
2. They also composed their literature in Tamil. The Nalayra Divyaprabandham of the Alvars and the Tevaram of the Nayanars were composed in Tamil.
3.  Virashaiva movement which was led by Basavanna made use of the kannada language to spread his messages.
4.  The use of Gujarati and Assamese language was also encouraged in Medieval period.
5. Guru Nanak and his successor preached their message through Punjabi. In Punjab the holy book of Sikhism, the Guru Granth Sahib was also composed in Punjabi.
6.  The saints of Maharashtra preached their message through Marathi. The chief saints preached through Marathi were saint Jnaneswar, Saint Tukaram and Guru Ramdas.
7.  The sufi who came to India from different comers of the world and settled here used the local languages to preach their teachings.
8.  In Delhi, the Chishti Sufi conversed in Hindavi.

Answer 12:

(a) Programme and objectives of the movement:

1.  It boycotted the foreign goods.
2.  It emphasized on the goods and things manufactured in India.
3.  Titles and honours conferred by the British government were returned.
4. Resignation by Indian members nominated in the local institution, resigned from their post.
5. Schools and colleges run by the British government were boycotted.
6.  Lawyers boycotted the civil courts.
7. The soldiers, clerks, and workers refused to render any service abroad.

(b) Importance of the non-cooperation movements

1. Due to the non-cooperation movement Congress came in direct clash with the British government.
2. It was for the first time in the history of India a mass movement was started across the country against the British empire.
3. The movement gave an opportunity to Indian industries to grow and establish firmly,
4. It speeded up Indian struggle to achieve freedom from, British empire the.

OR

1. Gandhiji felt that Puma Swaraj would not come on its own. It had to fight for achieving it. He was very much worried about government salt law.
2. In 1930, he decided to break this law. According to the law, the State had a monopoly on the manufacture and sale of salt.
3.  Mahatma Gandhi and other prominent leaders of the freedom struggle thought that it was sinful to tax salt because it is an essential item of our food. Both the rich and the poor needed it equally.
4.  Gandhiji felt that his salt march would become popular and would represent the general desire of freedom to a specific grievance shared by all.
5. On 6 April, 1930 Gandhiji along with his followers marched for over 240 miles from Sabarmati to the coastal town of Dandi.
6. They broke the government law by gathering natural salt found on the sea shore, and boiling sea water to produce salt.
7. A large number of people including women participated in this historic march. The government tried to crush the movement through brutal action against peaceful Satyagrahis.
8. Thousands were arrested and sent to jail. But the movement played a significant role in achieving freedom of India.

Answer 13:
Economic life:

1. Land was very fertile, hence agriculture was the main occupation of the people. It is believed that even the king used to plough the land.
2. Beside agriculture, animal rearing was the main occupation of the people.
3.  Trade also flourished during the age. It was controlled by trading guilds, who were given many facilities by the state.
4. People also practiced other occupations like carpenter, jewellers, potter, ironsmith, craftsmen, etc.

Social life:

1. At this time society was divided into four vamas. These vamas were the Brahman, Kshatriya, Vaishya and Shudra. Among them Brahmans occupied the highest rank in society.
2. Women occupied the respectable position. They have the right to choose their husbands. The royal princesses chose their husbands through swayamber.
3.  Mahabharata was the age of bravery. Dying in the battle field was considered as a symbol of prestige. Protection of the weaker section was also considered important.

OR

1. It provides us valuable description of social values prevailing in the society at that time.
2. Rules regarding patriliny successions were followed.
3.  It throws light on the caste system and interrelation of various caste groups prevalent in the society.
4. It is quite evident that society was patriarchal in nature.
5. Kanyadan was considered as an important religious duty of the fathers.
6. Different types of marriages were practiced in the society.
7.  It also throws light on the different vama and different professions practiced by the people. (viii) The elder male member of the society was more dominating.
8.  It also throws lights on the two contrasting social norms in the relationship between Pandavas and their mother and relation of Kauravas with their mother.

Answer 14:
(i) (a) They wanted to live a simple and disciplined life in sangha.
(b) They wanted to remain away from wordly pleasure.

(ii) (a) Bodh sangha was an organisation of monks, who served as teachers of Dhamma.
(b) They lived a simple life and possessed only those essential goods which were required in daily routine life.

(iii) (a) To make them conform to a simple life possessing only essential prerequisites for survival.
(b) avoid self indulgence
(c) Inculcate moderation in all aspects from food to clothing
(d) Inculcate discipline, respect for rules and develop a sense of sharing, fellow feeling and equality.

Answer 15:
(i) He had written
(a) Everything available on the earth can be bought here.
(b) There are a large number of merchants who made transaction of things.

(ii) (a) The universe efforts that the rulers made to store water and conduct it to the city.
(b) The well irrigated field and watered gardens, despite Vijayanagara being one of the most arid zones of the peninsula.

(iii) According to him
(a) Things available in bazaars were very cheap.
(b) The Bazaars were flooded with fruits.
(c) Every kind of meat was available in abundance.

Answer 16:
(i) (a) He was a doctor and specialist in the treatment of typhoid.
(b) When India was partitioned, he was posted at Dharampur in Himachal Pradesh.

(ii) (a) It provided variety of examples of written descriptions.
(b) It provides valuable materials to the historians for the reconstruction of the past.

(iii) (a) During his visit to Karachi his friends stayed with him at the place where he (Khushdeva Singh) was put up.
(b) They all remained with him until he stayed there.
(c) Before departing to India, he was offered a basket of grapes as a symbol of their love.

Answer 17:

(2) (A) Amaravati (B) Sanchi (C) Nasik

We hope the CBSE Sample Papers for Class 12 History Paper 4 help you. If you have any query regarding CBSE Sample Papers for Class 12 History Paper 4, drop a comment below and we will get back to you at the earliest.

These Sample papers are part of CBSE Sample Papers for Class 12 History Here we have given CBSE Sample Papers for Class 12 History Paper 3.

CBSE Sample Papers for Class 12 History Paper 3

Board	CBSE
Class	XII
Subject	History
Sample Paper Set	Paper 3
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 3 of Solved CBSE Sample Paper for Class 12 History is given below with free PDF download solutions.

Time: 3 Hours
Maximum Marks: 80

General Instructions

(i) Answer all the questions. Some questions have internal choice. Marks are indicated against each question.
(ii) Answer to question nos 1 to 3 carrying 2 marks should not exceed 30 words each.
(iii) Answer to question nos. 4 to 9 carrying 4 marks should not exceed 100 words. Students should attempt only 5 questions in this section.
(iv) Question 10 (for 4 marks) is a value based question and compulsory question.
(v) Answer to question nos 11 to 13 carrying 8 marks should not exceed 350 words.
(vi) Questions 14 -16 are source based questions and have no internal choice.
(vii) Question 17 is a map question includes ‘identification’ and significant’ test items.

PART – A

Answer all the questions given below:

Question 1:
Who was Harisena?

Question 2:
Why was Ibn-Battuta fond of travels? Give any two reasons.

Question 3:
Who were the Paharias? How did they earn their livelihood?

PART-B
Section-I

Answer any five of the following questions:

Question 4:
Mention the main subsistence methods of the Harappan people.

Question 5:
Who was Gotami-putra Satakami? What were his main achievements?

Question 6:
What was the common financial pool of Panchayat during 16 – 17th centuries? Mention its importance.

Question 7:
How did Akbar try to tie his empire in one thread? Discuss.

Question 8:
Elaborate the nature of the Revolt of 1857.

Question 9:
Gandhiji was as much a social reformer as he was a politician. Discuss.

Section II

Value Based Question

Question 10:
Read the following passage and answer the questions that follow.
Separate electorates was a “poison that has entered the body politic of our country” declared Sardar Patel. It was a demand that had turned one community against another, divided the nation, caused bloodshed and led to the tragic partition of the country.
Divide and rule was the policy of the British ruler and they had sown such seeds. Ultimately the tragic partition of the nation took place with bloodshed.
By which values the bloodshed might have been stopped?

PART-C

Answer any five of the following Questions:

Question 11:
Kanishka was known as second Asoka. Evaluate.
OR
Buddhism declined in India whereas Jainism remained there in some parts. Explain.

Question 12:
What were the similarities in Sufi and Bhakti traditions? Explain.
OR
What were the main features of the administration of rulers of Vijaynagar Empire? Discuss.

Question 13:
Why was the Lottery Committee constituted? What steps were taken for the town-planning in Calcutta?
OR
What methods were used to oppose the British Rule during the non-cooperation movement? Discuss.

PART-D

Source Based Questions

Question 14:
Read the following excerpts carefully and answer the questions that follows.

The Sudarshana Lake in Gujarat

Find Gimar on Map 2. The Sudarshana lake was an artificial reservoir. We know about it from a rock inscription (c. second century CE) in Sanskrit, composed to record the achievements of the Shaka ruler, Rudradaman.
The inscription mentions that the lake, with embankments and water channels, was built by a local governor during the rule of the Mauryas. However, a terrible storm broke the embankments and water gushed out of the lake. Rudradaman, who was then ruling in the area, claimed to have got the lake repaired using his own resources. Without imposing any tax on his subjects.
Another inscription on the same rock (c. fifth century) mentions how one of the rulers of the Gupta dynasty got the lake repaired once again.

1. Name two rulers whose names are associated with the repair work.
2. Who was Rudradaman? What is he best remembered for?
3.  Why did rulers make arrangements for irrigation?

Question 15:
Read the following excerpt carefully and answer the questions that follow.

The One Lord

Here is a composition attributed to Kabir: Tell me, brother, how can there be no one lord of the world but two? Who led you so astray? God is called by many names: Names like Allah, Ram, Karim, Keshav, Hari, and Hazrat. Gold may be shaped into rings and bangles. Isn’t it gold all the same? Distinctions are only words we invent. Kabir says they are both mistaken. Neither can find the only Ram. One kills the goat, the other cows. They waste their lives in disputation.

1.  What is Kabifs argument against distinction made between gods of different communities?
2. Give three teachings of Kabir.
3.  Differentiate between Nirgun and Sagun-Bhakti saints. Give one example of each.

Question 16:
Read the following excerpt carefully and answer the questions that follow.

What Talugdars thought

The attitude of the taluqdars was best expressed by Hanwant Singh, the Raja of Kalakankar, near Rae Bareli. During the mutiny, Hanwant Singh had given shelter to a British officer, and conveyed him to safety. While taking leave from the officer, Hanwant Singh told him:
Sahib, your countrymen came into this country and drove out our king. You sent your officers round the districts to examine the titles to the estates. At one blow you took from me lands which from time immemorial had been in my family. I submitted. Suddenly misfortune fell upon You. The people of the land rose against you. You came to me whom you had despoiled. I have saved you. But now, I march at the head of my retainers to Lucknow to try and drive you from the country.

1.  Why were the people angry according to Singh? What happened to his family?
2. What happened under the Summary Settlement of 1856. Explain.
3. What was the result of the dispossession of the Taluqdars? Explain.

Question 17:
(17.1) On the given political outline map of India, locate and label the following with appropriate symbols:
(a) Nageshwar
(b) Agra, the imperial capital of Mughal.
(17.2) On the same outline map of India, three centres related to the Indian National Movement have been marked as A, B and C. Identify them and write their correct names on the lines drawn near them.

Answers

Answer 1:
(i) Harisena was the poet laureate of the king Samudragupta.
(ii) He composed Prayag Prashasti in praise and honour of Samudragupta.

Answer 2:
(i) Ibn-Batuta loved travelling. He went to different places to explore new world and people.
(ii) He considered experience gained through travels as an important source of knowledge than the books.

Answer 3:
(i) The hill folk were known as the Paharias.
(ii) They earned their livelihood from the forest produce. They also practised shifting cultivation.

Answer 4:
(i) The Harappans got food from a wide range of plant and animal products.
(ii) Wheat, barley, lentil, chickpea and sesame were the main grains included in their food. From many Harappan sites grains have been found.
(iii) The people also ate rice and millet. Millet have been found from many sites in Gujarat. Rice was not used much as they are relatively rare.
(iv) Bones of deer and gharial have been found. It can be imagined that the people of Harappan civilization ate their flesh and meat. Its is not known that they hunted themselves or got their meat from other hunting groups.
(v) Harappan people got food from many animals like sheep, goat, buffalo and pig: All these – animals were domesticated.

Answer 5:
(i) Gotami-putra Satakami was the most brave king of Satavahana dynasty. Achievements:
(ii) He ruled from 106 CE to 130 CE and increased strength and prosperity of his dynasty.
(ii) He called himself the lone Brahmana and killed many kshatriyas. He defeated Shaka. Further he claimed to uproot the Kshatriya dynasty.
(iii) Nahapan was the important leader of this dynasty. Silver coins of Nahapan have been found. They might have been minted again. The empire of Satakami was spread from Malwa in North to Karnataka in South.

Answer 6:
(a) The expenditure of Panchayat was being run from that financial pool which was contributed by every individual.
(b) Importance:

1.  This pool was used for the cost of entertaining revenue officials who used to visit the village from time to time. It was used to pay salary to mugaddam and chowkidar.
2.  This pool was also used to meet expenses for community welfare activities like flood and other natural calamities.
3.  These funds were used for community works like construction of a bund or digging a canal which peasants were unable to afford on their own.

Answer 7:
(i) Akbar gave preference to national interests instead of developing any religion. He conquered whole of north India and tied it in one thread.
(ii) Akbar implemented same legal and administrative system in all of his provinces. In medieval period, Hindus were given same religious freedom like Muslims.
(iii) Akbar abolished the religious tax imposed on Hindus called Jizya. He married Rajput princess and permitted her to worship their deities according to Hinda traditions.
(iv) Din-e-Ilahi was a symbol of religious tolerance of Akbar. He began this religion to establish unity among Hindus and Muslims. Just because of these measures, Akbar succeeded in his mission.

Answer 8:
(i) The people belonging to all sections of society participated in the revolt of 1857. The people as well as the soldiers were against the British.
(ii) Indians wanted to get rid of the oppression committed by the British. The soldiers revolted, not to accept any princely state, but to expel the British from India.
(iii) The rebellion did not spread in many parts of India. Many cities remained calm and quiet. But it did not mean that they did not like freedom.
(iv) Both the Hindus and the Muslims fought unitedly. It is evident that they were not happy with the imperial rule. They took up arms to send the British out of India.

Answer 9:
(i) There is no denying the fact that Gandhiji was as much a social reformer as he was a politician. As a politician, he transformed Indian National Movement into a broad mass movement.
(ii) He (Gandhiji) was arrested in 1922 and was released from the jail in February 1924. He devoted his attention to encourage the home spun Khadi cloth and to eradicate untouchability from the society.
(iii) Gandhiji believed that Indians need to remove social evils like child marriage and untouchability in order to be worthy of freedom. He was of the view that all of us must prepare an atmosphere of harmony among different religious communities.
(iv) Gandhiji stressed on Hindu-Muslim harmony. He believed that Indians had to learn to become self reliant on economic front.

Answer 10:
Expected values:

1. Communal harmony
2. Sense of peace and harmony.
3. Not fight for the sake of humanity
4. Feeling of co-existence.

Answer 11:

1. Kanishka was a brave soldier. He was a great patron of art and a great propagandist of religion.
2. Kanishka was a great conqueror. He expanded his empire that was transfered from his ancestors. Chinese victory was known as his biggest victory.
3. He was very effective and successful ruler. Moreover, entire authority of the kingdom was in his hands. Empire was divided into several provinces. ‘Kshatrap’ was the head of the province.
4. Kanishka was a great patron and lover of art. He founded four cities; decorated these cities with pillars and sculptures. Gandhara art form was developed and flourished under his patronage. ‘Chaity’ of Peshawar made by Kanishka is the unique example of art form.
5. He was a great patron of scholars and literary persons. There were many great scholars like Ashwaghosha, Vasumitra, Nagarjuna in his court.
6. He was a religious king. Buddhism was spread by him in different parts of the world. He set up many monastries, provided monetary help to the monks. Fourth Conference of Buddhism was called by him. Necessary reforms were introduced by him in Buddhism. Mahayana, sect of Buddhism came into being during his age.
7. Kanishka propagated Buddhism as Asoka did. He helped Buddhist monks and sent many persons to foreign countries to propagate Buddhism.
8. He tried to remove defects of Buddhism, organised a conference. Due to his services for Buddhism, he is known as second Asoka.

OR

1.  Buddhism grew and declined very rapidly in India. But the existence of Jainism remained . in different parts of India.
2.  It became very complex as time passed. Lot of evils and unnecessary customs and traditions were included in it, so people left it.
3. Teachings of Buddha were started to be compile in Sanskrit language by the followers of Buddhism. Common masses were not able to understand the language, hence popularity of Buddhism declined.
4.  Buddhist monks were of high character but gradually lots of a lowlessness came in their character. They sharted to live in lavish atmosphere. Adverse impacts were also observed among the people.
5. (After the death of Harsha, Buddhism could not receive help from the state. So, the popularity of Buddhism began to decline.
6. Mahayana and Hinayana, the two branches of Buddhism emerged during the reign of Kanishka. No big difference between these two branches. Many followers of the Mahayana again inducted into Hinduism.
7.  Beyond Mauryan empire, Pushyamitra Shunga commited outrage on Buddhists. He killed lot of Buddhists. People were scared by this and they left Buddhism.
8.  Many invaders attacked many Mathas and Viharas and broke them down. Many Buddhists were killed by them, so it declined to a great extent.

Answer 12:

1. The emerging places of Sufi and Bhakti movements were different. The ideologies of both movements had many similarities.
2.  They considered man as the main subject. According to them, all human beings should live in peace and harmony.
3.  These movements believed in one God. As the Sufis stated that God is one and all of us are his children. Whereas the saints of Bhakti movement sang hymns in praise of God.
4. The saints of both Sufi and Bhakti movements advised their followers to love the human beings which leads to love for God.
5.  The Sufi saints and Bhakts have praised Guru in their hymns. Pir, this term was used as Guru by Sufi saints. It was the only difference between both movements.
6.  Teachings of tolerance were communicated by the Sufis and Bhakts among their followers- Hindus and Muslims. They should live peacefully and unitedy.
7. Saints of both movements propagated the teachings of love, harmony and welfare.
8.  There were great similarities between the Sufis and Bhakts regarding the Nature, God and other things.

OR
The main features of the administration of rulers of Vijaynagar Empire were as follows.

1. The chief of the central administration in Vijaynagar was the king himself. He held all the powers of administration.
2.  There was a council which helped the king in different issues.
3. There were 200 provinces in the state of Vijaynagar. Prantpati was known as the chief of the province. They belonged to the royal family. Sometimes many of them belonged to powerful and wealthy families.
4. Every province was divided into districts and districts were divided into pargamas and they were divided into villages.
5. Powerful army was there to provide the protection for the state. Horses, elephants were there in the army and brave soldiers were deployed in the army.
6.  King was the chief justice of the state himself. The prantpati or subedar delivered the justice in the provinces. The punishments were very severe.
7. The main source of income of the state was land revenue. Farmers had to pay 1/6 to l,/4 of produce of the crop as the land revenue.
8. Farmers were wealthy and enjoyed a comfortable life. Generally, no economic crisis.

Answer 13:
(a) Nature of Lottery Committee:

1. The Lottery Committee was constituted in 1817 to help the government in carrying * out the work of town planning in Calcutta.
2. The committee was named as the Lottery Committee because it raised funds for the development of the town through public lotteries.
3. No funds were provided by the governments for the development of cities and town planning.
4.  The funds of town planning were raised by responsible public-minded citizens.
5. Various steps were taken by the Lottery Committee for the development of Calcutta.
6.  The Lottery Committee commissioned a new map of Calcutta so that it could have a comprehensive picture of the city.
7. ( It took up road building in the area of the city where the Indians lived mostly.
8. All the encroachments from the banks of the rivers were removed by the committee.
   The committee removed several huts to beautify and clean the city all round.
9. Due to the demolition of the huts, many poor labourers were displaced. They were sent to the outskirts of Calcutta by the committee.

OR

1.  The Non-cooperation Movement was launched by Mahatma Gandhi in 1920. It had a set programme for the Indians to follow.
2.  The students were asked not to attend their schools and colleges for indefinite period,
3. The lawyers were asked to boycott the law courts.
4.  The common people were asked to renounce voluntary association with the British government.
5.  Workers started strikes in various towns and cities. 396 strikes were carried out in different cities in 1921. Six lakh workers were involved. Seven million working days were lost.
6. The hill tribes in Northern Part of Andhra Pradesh violated the forest laws.
7. Peasants in Awadh did not pay taxes. Further they neglected to carry loads of colonial officials in Kumaun.
8. Above mentioned methods were laid down for all the protestors. Lot of then adopted the methods which suited their interests.

Answer 14:
(i) (a) Shaka ruler Rudradaman I and
(b) One of the rulers of the Gupta dynasty.

(ii) (a) Rudradaman was the most famous Shaka ruler in India. He ruled over Sindh, part
of Gujarat, Konkan, Narmada valley, Malwa and Kathiawar
(b) He is best remembered in history because of the work a he undertook to improve the Sudarshan lake using his own resources without imposing any tax on his subjects.

(iii) (a) Increase land under cultivation.
(b) To enable application of new transplantation technique for rice cultivation, to increase rice production.
(c) To enable equal supply of the resource i.e. water and that was the strategy of state controlling all economic activity.

Answer 15:
(i) By his arguments, Kabir emphasised the unity of God. He is called by various names Allah, Ram, Karim, Keshav and Hazrat. Hindus and Muslims worship the ultimate being. With the following example, Kabir convinced the people like the moulded into various shapes and forms as known bangles, rings, pendant etc.

(ii) (a) Kabir’s teachings emphasised that Hindus and Muslims are one and worship the same god.
(b) He urged the Hindus and Muslims to give up external religion.
(c) Emphasised fundamental unity of man and preached a religion of love. He used Sufi concept of Zikr and Ishq.

(iii) Sagun bhakti: worship of God with form e.g. Mirabai.
Nirgun Bhakti-worship of god without form e.g. Kabir and Nanak.

Answer 16:
(i) The people were angry because the British had overthrown the king. The titles of the estates were re-examined by the officers. People’s lands had been taken away including his, which had been in his family for generations.
(ii) There was assumption among the British that the Taluqdars were removed whereever possible whereby the taluqdars now held only 38% of the land in Awadh.
(iii) (a) Due to dispossession the taluqdars were hard hit, they lost more than 1/2 the villages that they had held.
(b) They were disarmed and their forts destroyed.
(c) They lost their power and prestige and their autonomy ended.

Answer 17:

(2) (A) Calcutta (B) Kanpur (C) Bombay

 

We hope the CBSE Sample Papers for Class 12 History Paper 3 help you. If you have any query regarding CBSE Sample Papers for Class 12 History Paper 3, drop a comment below and we will get back to you at the earliest.