MCQ Questions for Class 11 Maths Chapter 1 Sets with Answers

Check the below NCERT MCQ Questions for Class 11 Maths Chapter 1 Sets with Answers Pdf free download. MCQ Questions for Class 11 Maths with Answers were prepared based on the latest exam pattern. We have provided Sets Class 11 Maths MCQs Questions with Answers to help students understand the concept very well.

Class 11 Maths Chapter 1 MCQ With Answers

Maths Class 11 Chapter 1 MCQs On Sets

Sets Class 11 MCQ Question 1.
If A, B and C are any three sets, then A – (B ∪ C) is equal to
(a) (A – B) ∪ (A – C)
(b) (A – B) ∪ C
(c) (A – B) ∩ C
(d) (A – B) ∩ (A – C)

Answer

Answer: (d) (A – B) ∩ (A – C)
Hint:
Given A, B and C are any three sets.
Now, A – (B ∪ C) = (A – B) ∩ (A – C)

Sets MCQ Questions Class 11 Question 2.
(A’)’ = ?
(a) ∪ – A
(b) A’
(c) ∪
(d) A

Answer

Answer: (d) A
Hint:
(A’)’ = A

MCQ On Sets Class 11 Question 3.
A – B is read as?
(a) Difference of A and B of B and A
(b) None of the above
(c) Difference of B and A
(d) Both a and b

Answer

Answer: (a) Difference of A and B of B and A
Hint:
A – B will read as difference of A and B of B and A
Ex: Let A = {1, 2, 3, 4, 5} and B = {1, 3, 5, 7}
Now, A – B = {2, 4}

Class 11 Sets MCQ Questions Question 4.
If A, B and C are any three sets, then A × (B ∪ C) is equal to
(a) (A × B) ∪ (A × C)
(b) (A ∪ B) × (A ∪ C)
(c) None of these
(d) (A × B) ∩ (A × C)

Answer

Answer: (a) (A × B) ∪ (A × C)
Hint:
Given A, B and C are any three sets.
Now, A × (B ∪ C) = (A × B) ∪ (A × C)

MCQ Of Sets Class 11 Question 5.
IF A = [5, 6, 7] and B = [7, 8, 9] then A ∪ B is equal to
(a) [5, 6, 7, 8, 9]
(b) [5, 6, 7]
(c) [7, 8, 9]
(d) None of these

Answer

Answer: (a) [5, 6, 7, 8, 9]
Hint:
Given A = [5, 6, 7] and B = [7, 8, 9]
then A ∪ B = [5, 6, 7, 8, 9]

Class 11 Maths Chapter 1 MCQ Question 6.
Which of the following sets are null sets
(a) {x: |x |< -4, x ?N}
(b) 2 and 3
(c) Set of all prime numbers between 15 and 19
(d) {x: x < 5, x > 6}

Answer

Answer: (b) 2 and 3
Hint:
2 and 3 is the null set.

Class 11 Maths Chapter 1 MCQ With Answers Question 7.
IF R = {(2, 1),(4, 3),(4, 5)}, then range of the function is?
(a) Range R = {2, 4}
(b) Range R = {1, 3, 5}
(c) Range R = {2, 3, 4, 5}
(d) Range R {1, 1, 4, 5}

Answer

Answer: (b) Range R = {1, 3, 5}
Hint:
Given R = {(2, 1),(4, 3),(4, 5)}
then Range(R) = {1, 3, 5}

Class 11 Maths MCQ Chapter 1 Question 8.
The members of the set S = {x | x is the square of an integer and x < 100} is
(a) {0, 2, 4, 5, 9, 58, 49, 56, 99, 12}
(b) {0, 1, 4, 9, 16, 25, 36, 49, 64, 81}
(c) {1, 4, 9, 16, 25, 36, 64, 81, 85, 99}
(d) {0, 1, 4, 9, 16, 25, 36, 49, 64, 121}

Answer

Answer: (b) {0, 1, 4, 9, 16, 25, 36, 49, 64, 81}
Hint:
The set S consists of the square of an integer less than 100
So, S = {0, 1, 4, 9, 16, 25, 36, 49, 64, 81}

Class 11 Maths Ch 1 MCQ Question 9.
In a class of 120 students numbered 1 to 120, all even numbered students opt for Physics, whose numbers are divisible by 5 opt for Chemistry and those whose numbers are divisible by 7 opt for Math. How many opt for none of the three subjects?
(a) 19
(b) 41
(c) 21
(d) 57

Answer

Answer: (b) 41
Hint:
The number of students who took at least one of the three subjects can be found by finding out A ∪ B ∪ C, where A is the set of those who took Physics, B the set of those who took Chemistry and C the set of those who opted for Math.
Now, A ∪ B ∪ C = A + B + C – (A ∩ B + B ∩ C + C ∩ A) + (A ∩ B ∩ C)
A is the set of those who opted for Physics = 120/2 = 60 students
B is the set of those who opted for Chemistry = 120/5 = 24
C is the set of those who opted for Math = 120/7 = 17
The 10th, 20th, 30th….. numbered students would have opted for both Physics and Chemistry.
Therefore, A ∩ B = 120/10 = 12
The 14th, 28th, 42nd….. Numbered students would have opted for Physics and Math.
Therefore, C ∩ A = 120/14 = 8
The 35th, 70th…. numbered students would have opted for Chemistry and Math.
Therefore, B ∩ C = 120/35 = 3
And the 70th numbered student would have opted for all three subjects.
Therefore, A ∪ B ∪ C = 60 + 24 + 17 – (12 + 8 + 3) + 1 = 79
Number of students who opted for none of the three subjects = 120 – 79 = 41

MCQ Questions For Class 11 Maths With Answers Chapter 1 Question 10.
{ (A, B) : A² +B² = 1} on the sets has the following relation
(a) reflexive
(b) symmetric
(c) none
(d) reflexive and transitive

Answer

Answer: (b) symmetric
Hint:
Given {(a, b) : a² + b² = 1} on the set S.
Now a² +b² = b² + a² = 1
So, the given relation is symmetric.

MCQ Class 11 Maths Chapter 1 Question 11.
Two finite sets have N and M elements. The number of elements in the power set of first set is 48 more than the total number of elements in power set of the second test. Then the value of M and N are
(a) 7, 6
(b) 6, 4
(c) 7, 4
(d) 6, 3

Answer

Answer: (b) 6, 4
Hint:
Let A and B be two sets having m and n numbers of elements respectively
Number of subsets of A = 2m
Number of subsets of B = 2n
Now, according to question
2m – 2n = 48
⇒ 2n(2m – n – 1) = 24(22 – 1)
So, n = 4
and m – n = 2
⇒ m – 4 = 2
⇒ m = 2 + 4
⇒ m = 6

MCQ Questions On Sets Class 11 Question 12.
The range of the function f(x) = 3x – 2‚ is
(a) (- ∞, ∞)
(b) R – {3}
(c) (- ∞, 0)
(d) (0, – ∞)

Answer

Answer: (a) (- ∞, ∞)
Hint:
Let the given function is
y = 3x – 2
⇒ y + 2 = 3x
⇒ x = (y + 2)/3
Now x is saisfied by all values.
So, Range{f(x)} = R = (-∞, ∞)

Ch 1 Maths Class 11 MCQ Question 13.
If A, B, C be three sets such that A ∪ B = A ∪ C and A ∩ B = A ∩ C, then,
(a) B = C
(b) A = C
(c) A = B = C
(d) A = B

Answer

Answer: (a) B = C
Hint:
Given A, B, C be three sets such that A ∪ B = A ∪ C and A ∩ B = A ∩ C then B = C

MCQ On Sets For Class 11 Pdf With Answers Question 14.
In 2nd quadrant?
(a) X < 0, Y < 0
(b) X < 0, Y > 0
(c) X > 0, Y > 0
(d) X > 0, Y < 0

Answer

Answer: (b) X < 0, Y > 0
Hint:
In the second quadrant,
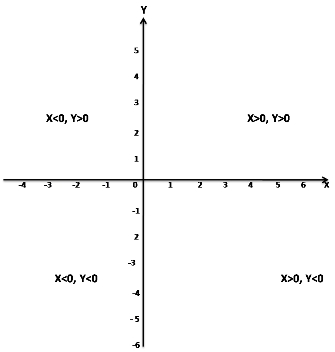
MCQ Questions for Class 11 Maths Chapter 1 Sets with Answers 1
X < 0, Y > 0

MCQ Of Chapter Sets Class 11 Question 15.
How many rational and irrational numbers are possible between 0 and 1?
(a) 0
(b) Finite
(c) Infinite
(d) 1

Answer

Answer: (c) Infinite
Hint:
There are infinite many rational and irrational numbers are possible between 0 and 1
This is because between any two numbers, there are infinite numbers.

Question 16.
Empty set is a?
(a) Finite Set
(b) Invalid Set
(c) None of the above
(d) Infinite Set

Answer

Answer: (a) Finite Set
Hint:
In mathematics, and more specifically set theory, the empty set is the unique set having no elements and its size or cardinality (count of elements in a set) is zero.
So, an empty set is a finite set.

Question 17.
If A = [5, 6, 7] and B = [7, 8, 9] then A U B is equal to
(a) [5, 6, 7, 8, 9]
(b) [5, 6, 7]
(c) [7, 8, 9]
(d) None of these

Answer

Answer: (a) [5, 6, 7, 8, 9]
Hint:
Given A = [5, 6, 7] and B = [7, 8, 9]
then A U B = [5, 6, 7, 8, 9]

Question 18.
Which of the following two sets are equal?
(a) A = {1, 2} and B = {1}
(b) A = {1, 2} and B = {1, 2, 3}
(c) A = {1, 2, 3} and B = {2, 1, 3}
(d) A = {1, 2, 4} and B = {1, 2, 3}

Answer

Answer: (c) A = {1, 2, 3} and B = {2, 1, 3}
Hint:
Two sets are equal if and only if they have the same elements.
So, A = {1, 2, 3} and B = {2, 1, 3} are equal sets.

Question 19.
In a class of 50 students, 10 did not opt for math, 15 did not opt for science and 2 did not opt for either. How many students of the class opted for both math and science.
(a) 24
(b) 25
(c) 26
(d) 27

Answer

Answer: (d) 27
Hint:
Total students = 50
Students who did not opt for math = 10
Students who did not opt for Science = 15
Students who did not opt for either maths or science = 2
Total of 40 students in math and 13 did not opt for science but did for math = 40 – 13 = 27
So, students of the class opted for both math and science is 27

Question 20.
In last quadrant?
(a) X < 0, Y > 0
(b) X < 0, Y < 0
(c) X > 0, Y < 0
(d) X > 0, Y > 0

Answer

Answer: (d) X > 0, Y > 0
Hint:
In the last quadrant,
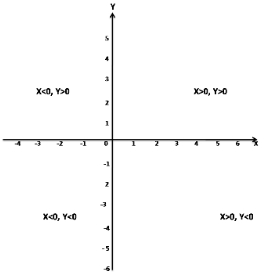
MCQ Questions for Class 11 Maths Chapter 1 Sets with Answers 2
X > 0, Y > 0

We hope the given NCERT MCQ Questions for Class 11 Maths Chapter 1 Sets with Answers Pdf free download will help you. If you have any queries regarding CBSE Class 11 Maths Sets MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.

Class 11 Maths MCQ: