Check the below NCERT MCQ Questions for Class 11 Maths Chapter 6 Linear Inequalities with Answers Pdf free download. MCQ Questions for Class 11 Maths with Answers were prepared based on the latest exam pattern. We have provided Linear Inequalities Class 11 Maths MCQs Questions with Answers to help students understand the concept very well.
Linear Inequalities Class 11 MCQs Questions with Answers
Linear Inequalities Class 11 MCQ Question 1.
Sum of two rational numbers is ______ number.
(a) rational
(b) irrational
(c) Integer
(d) Both 1, 2 and 3
Answer
Answer: (a) rational
Hint:
The sum of two rational numbers is a rational number.
Ex: Let two rational numbers are 1/2 and 1/3
Now, 1/2 + 1/3 = 5/6 which is a rational number.
MCQ On Linear Inequalities Class 11 Question 2.
If x² = -4 then the value of x is
(a) (-2, 2)
(b) (-2, ∞)
(c) (2, ∞)
(d) No solution
Answer
Answer: (d) No solution
Hint:
Given, x² = -4
Since LHS ≥ 0 and RHS < 0
So, No solution is possible.
Class 11 Maths Chapter 6 MCQ With Answers Question 3.
Solve: (x + 1)² + (x² + 3x + 2)² = 0
(a) x = -1, -2
(b) x = -1
(c) x = -2
(d) None of these
Answer
Answer: (b) x = -1
Hint:
Given, (x + 1)² + (x² + 3x + 2)² = 0
This is true when each term is equal to zero simultaneously,
So, (x + 1)² = 0 and (x² + 3x + 2)² = 0
⇒ x + 1 = 0 and x² + 3x + 2 = 0
⇒ x = -1, and x = -1, -2
Now, the common solution is x = -1
So, solution of the equation is x = -1
Linear Inequalities Objective Questions Class 11 Question 4.
If (x + 3)/(x – 2) > 1/2 then x lies in the interval
(a) (-8, ∞)
(b) (8, ∞)
(c) (∞, -8)
(d) (∞, 8)
Answer
Answer: (a) (-8, ∞)
Hint:
Given,
(x + 3)/(x – 2) > 1/2
⇒ 2(x + 3) > x – 2
⇒ 2x + 6 > x – 2
⇒ 2x – x > -2 – 6
⇒ x > -8
⇒ x ∈ (-8, ∞)
Linear Inequalities MCQ Questions Question 5.
The region of the XOY-plane represented by the inequalities x ≥ 6, y ≥ 2, 2x + y ≤ 10 is
(a) unbounded
(b) a polygon
(c) none of these
(d) exterior of a triangle
Answer
Answer: (c) none of these
Hint:
Given inequalities x ≥ 6, y ≥ 2, 2x + y ≤ 10
Now take x = 6, y = 2 and 2x + y = 10
when x = 0, y = 10
when y = 0, x = 5
So, the points are A(6, 2), B(0, 10) and C(5, 0)
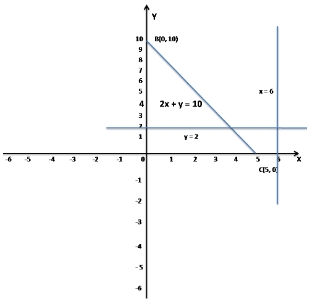
So, the region of the XOY-plane represented by the inequalities x ≥ 6, y ≥ 2, 2x + y ≤ 10 is not defined.
MCQ Of Chapter 6 Maths Class 11 Question 6.
The interval in which f(x) = (x – 1) × (x – 2) × (x – 3) is negative is
(a) x > 2
(b) 2 < x and x < 1
(c) 2 < x < 1 and x < 3
(d) 2 < x < 3 and x < 1
Answer
Answer: (d) 2 < x < 3 and x < 1
Hint:
Given, f(x) = (x – 1) × (x – 2) × (x – 3) has all factors with odd powers.
So, put them zero
i.e. x – 1 = 0, x – 2 = 0, x – 3 = 0
⇒ x = 1, 2, 3
Now, f(x) < 0 when 2 < x < 3 and x < 1
MCQ Of Linear Inequalities Class 11 Question 7.
If -2 < 2x – 1 < 2 then the value of x lies in the interval
(a) (1/2, 3/2)
(b) (-1/2, 3/2)
(c) (3/2, 1/2)
(d) (3/2, -1/2)
Answer
Answer: (b) (-1/2, 3/2)
Hint:
Given, -2 < 2x – 1 < 2
⇒ -2 + 1 < 2x < 2 + 1
⇒ -1 < 2x < 3
⇒ -1/2 < x < 3/2
⇒ x ∈(-1/2, 3/2)
Linear Inequalities Class 11 MCQ Questions Question 8.
The solution of the inequality |x – 1| < 2 is
(a) (1, ∞)
(b) (-1, 3)
(c) (1, -3)
(d) (∞, 1)
Answer
Answer: (b) (-1, 3)
Hint:
Given, |x – 1| < 2
⇒ -2 < x – 1 < 2
⇒ -2 + 1 < x < 2 + 1
⇒ -1 < x < 3
⇒ x ∈ (-1, 3)
Linear Inequalities Class 11 MCQ Pdf Question 9.
If | x − 1| > 5, then
(a) x∈(−∞, −4)∪(6, ∞]
(b) x∈[6, ∞)
(c) x∈(6, ∞)
(d) x∈(−∞, −4)∪(6, ∞)
Answer
Answer: (d) x∈(−∞, −4)∪(6, ∞)
Hint:
Given |x−1| >5
Case 1:
(x – 1) > 5
⇒ x > 6
⇒ x ∈ (6,∞)
Case 2:
-(x – 1) > 5
⇒ -x + 1 > 5
⇒ -x > 4
⇒ x < -4
⇒ x ∈ (−∞, −4)
So the range of x is (−∞, −4)∪(6, ∞)
MCQ Questions On Linear Inequalities Class 11 Question 10.
The solution of |2/(x – 4)| > 1 where x ≠ 4 is
(a) (2, 6)
(b) (2, 4) ∪ (4, 6)
(c) (2, 4) ∪ (4, ∞)
(d) (-∞, 4) ∪ (4, 6)
Answer
Answer: (b) (2, 4) ∪ (4, 6)
Hint:
Given, |2/(x – 4)| > 1
⇒ 2/|x – 4| > 1
⇒ 2 > |x – 4|
⇒ |x – 4| < 2
⇒ -2 < x – 4 < 2
⇒ -2 + 4 < x < 2 + 4
⇒ 2 < x < 6
⇒ x ∈ (2, 6) , where x ≠ 4
⇒ x ∈ (2, 4) ∪ (4, 6)
Linear Inequalities MCQs Pdf Question 11.
If (|x| – 1)/(|x| – 2) ≥ 0, x ∈ R, x ± 2 then the interval of x is
(a) (-∞, -2) ∪ [-1, 1]
(b) [-1, 1] ∪ (2, ∞)
(c) (-∞, -2) ∪ (2, ∞)
(d) (-∞, -2) ∪ [-1, 1] ∪ (2, ∞)
Answer
Answer: (d) (-∞, -2) ∪ [-1, 1] ∪ (2, ∞)
Hint:
Given, (|x| – 1)/(|x| – 2) ≥ 0
Let y = |x|
So, (y – 1)/(y – 2) ≥ 0
⇒ y ≤ 1 or y > 2
⇒ |x| ≤ 1 or |x| > 2
⇒ (-1 ≤ x ≤ 1) or (x < -2 or x > 2)
⇒ x ∈ [-1, 1] ∪ (-∞, -2) ∪ (2, ∞)
Hence the solution set is:
x ∈ (-∞, -2) ∪ [-1, 1] ∪ (2, ∞)
Class 11 Linear Inequalities MCQ Question 12.
The solution of the -12 < (4 -3x)/(-5) < 2 is
(a) 56/3 < x < 14/3
(b) -56/3 < x < -14/3
(c) 56/3 < x < -14/3
(d) -56/3 < x < 14/3
Answer
Answer: (d) -56/3 < x < 14/3
Hint:
Given inequality is :
-12 < (4 -3x)/(-5) < 2
⇒ -2 < (4-3x)/5 < 12
⇒ -2 × 5 < 4 – 3x < 12 × 5
⇒ -10 < 4 – 3x < 60
⇒ -10 – 4 < -3x < 60-4
⇒ -14 < -3x < 56
⇒ -56 < 3x < 14
⇒ -56/3 < x < 14/3
Inequalities MCQ Questions Question 13.
If x² = -4 then the value of x is
(a) (-2, 2)
(b) (-2, ∞)
(c) (2, ∞)
(d) No solution
Answer
Answer: (d) No solution
Hint:
Given, x² = -4
Since LHS ≥ 0 and RHS < 0
So, No solution is possible.
Question 14.
Solve: |x – 3| < 5
(a) (2, 8)
(b) (-2, 8)
(c) (8, 2)
(d) (8, -2)
Answer
Answer: (b) (-2, 8)
Hint:
Given, |x – 3| < 5
⇒ -5 < (x – 3) < 5
⇒ -5 + 3 < x < 5 + 3
⇒ -2 < x < 8
⇒ x ∈ (-2, 8)
Question 15.
The graph of the inequations x ≥ 0, y ≥ 0, 3x + 4y ≤ 12 is
(a) none of these
(b) interior of a triangle including the points on the sides
(c) in the 2nd quadrant
(d) exterior of a triangle
Answer
Answer: (b) interior of a triangle including the points on the sides
Hint:
Given inequalities x ≥ 0, y ≥ 0, 3x + 4y ≤ 12
Now take x = 0, y = 0 and 3x + 4y = 12
when x = 0, y = 3
when y = 0, x = 4
So, the points are A(0, 0), B(0, 3) and C(4, 0)
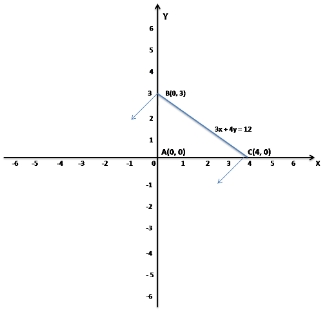
So, the graph of the inequations x ≥ 0, y ≥ 0, 3x + 4y ≤ 12 is interior of a triangle including the points on the sides.
Question 16.
If |x| < 5 then the value of x lies in the interval
(a) (-∞, -5)
(b) (∞, 5)
(c) (-5, ∞)
(d) (-5, 5)
Answer
Answer: (d) (-5, 5)
Hint:
Given, |x| < 5
It means that x is the number which is at distance less than 5 from 0
Hence, -5 < x < 5
⇒ x ∈ (-5, 5)
Question 17.
Solve: f(x) = {(x – 1)×(2 – x)}/(x – 3) ≥ 0
(a) (-∞, 1] ∪ (2, ∞)
(b) (-∞, 1] ∪ (2, 3)
(c) (-∞, 1] ∪ (3, ∞)
(d) None of these
Answer
Answer: (b) (-∞, 1] ∪ (2, 3)
Hint:
Given, f(x) = {(x – 1)×(2 – x)}/(x – 3) ≥ 0
or f(x) = -{(x – 1)×(2 – x)}/(x – 3)
which gives x – 3 ≠ 0
⇒ x ≠ 3
Using number line rule as shown in the figure,
which gives f(x) ≥ 0 when x ≤ 1 or 2 ≤ x < 3
i.e. x ∈ (-∞, 1] ∪ (2, 3)
Question 18.
If x² = 4 then the value of x is
(a) -2
(b) 2
(c) -2, 2
(d) None of these
Answer
Answer: (c) -2, 2
Hint:
Given, x² = 4
⇒ x² – 4 = 0
⇒ (x – 2)×(x + 2) = 0
⇒ x = -2, 2
Question 19.
The solution of the 15 < 3(x – 2)/5 < 0 is
(a) 27 < x < 2
(b) 27 < x < -2
(c) -27 < x < 2
(d) -27 < x < -2
Answer
Answer: (a) 27 < x < 2
Hint:
Given inequality is:
15 < 3(x-2)/5 < 0
⇒ 15 × 5 < 3(x-2) < 0 × 5
⇒ 75 < 3(x-2) < 0
⇒ 75/3 < x-2 < 0
⇒ 25 < x-2 < 0
⇒ 25 +2 < x <0+2
⇒ 27 < x < 2
Question 20.
Solve: 1 ≤ |x – 1| ≤ 3
(a) [-2, 0]
(b) [2, 4]
(c) [-2, 0] ∪ [2, 4]
(d) None of these
Answer
Answer: (c) [-2, 0] ∪ [2, 4]
Hint:
Given, 1 ≤ |x – 1| ≤ 3
⇒ -3 ≤ (x – 1) ≤ -1 or 1 ≤ (x – 1) ≤ 3
i.e. the distance covered is between 1 unit to 3 units
⇒ -2 ≤ x ≤ 0 or 2 ≤ x ≤ 4
Hence, the solution set of the given inequality is
x ∈ [-2, 0] ∪ [2, 4]
We hope the given NCERT MCQ Questions for Class 11 Maths Chapter 6 Linear Inequalities with Answers Pdf free download will help you. If you have any queries regarding CBSE Class 11 Maths Linear Inequalities MCQs Multiple Choice Questions with Answers, drop a comment below and we will get back to you soon.