ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Chapter Test
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Chapter Test
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Chapter Test
Question 1.
In the given figure, ∠1 = ∠2 and ∠3 = ∠4. Show that PT x QR = PR x ST.
Solution:
Given: In the given figure,
∠1 = ∠1 and ∠3 = ∠4
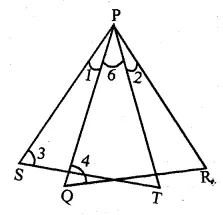
To prove : PT × QR = PR × ST
Proof: ∠1 = ∠2
Adding ∠6 to both sides
∠1 + ∠6 = ∠2 + ∠6
∠SPT = ∠QPR
In ∆PQR and ∆PST

Question 2.
In the adjoining figure, AB = AC. If PM ⊥ AB and PN ⊥ AC, show that PM x PC = PN x PB.
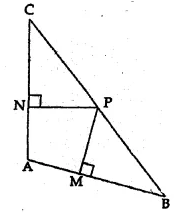
Solution:
Given : In the given figure,
AB = AC, PM ⊥ AB and PN ⊥ AC
To prove : PM × PC = PN × PB
Proof: In ∆ABC, AB = AC
∠B = ∠C
Now in ∆CPN and ∆BPM,

Question 3.
(a) In the figure (1) given below. ∠AED = ∠ABC. Find the values of x and y.
(b) In the fig. (2) given below, CD = \(\\ \frac { 1 }{ 2 } \) AC, B is mid-point of AC and E is mid-point of DF. If BF || AG, prove that :
(i) CE || AG
(ii) 3 ED = GD.
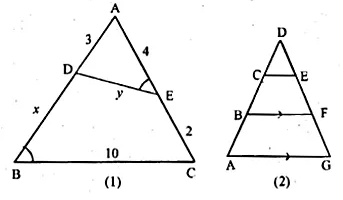
Solution:
(a) Given : In following figure, ∠AED = ∠ABC
Required: The values of x and y.
Now, in ∆ABC and ∆ADE
∠AED = ∠ABC (given)
∠A = ∠A (common)
∴ ∆ABC ~ ∆ADE
(By A.A. axiom of similarity)



Question 4.
In the given figure, 2 AD = BD, E is mid-point of BD and F is mid-point of AC and EC || BH. Prove that:
(i) DF || BH
(ii) AH = 3 AF.
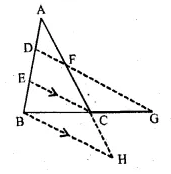
Solution:
Given: E is the mid-point of BD
and F is mid-point of AC
also 2 AD = BD and EC || BH
To Prove : (i) DF || BH
(ii) AH = 3 AF


Question 5.
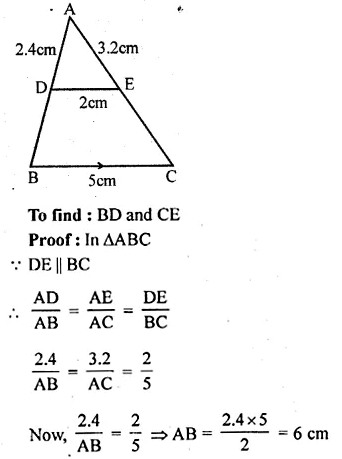
In a ∆ABC, D and E are points on the sides AB and AC respectively such that DE || BC. If AD = 2.4 cm, AE = 3.2 cm, DE = 2 cm and BC = 5 cm, find BD and CE.
Solution:
Given : In ∆ABC, D and E are the points
on the sides AB and AC respectively
DE || BC
AD = 2.4 cm, AE = 3.2 cm,
DE = 2 cm, BC = 5 cm
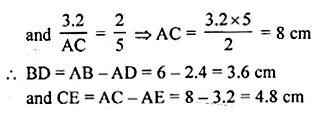
Question 6.
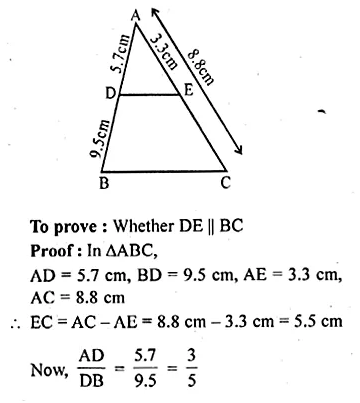
In a ∆ABC, D and E are points on the sides AB and AC respectively such that AD = 5.7cm, BD = 9.5cm, AE = 3.3cm and AC = 8.8cm. Is DE || BC? Justify your answer.
Solution:
In ∆ABC, D and E are points on the sides AB and AC respectively
AD = 5.7 cm, BD = 9.5 cm, AE = 3.3 cm and AC = 8.8 cm
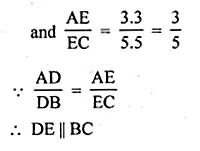
Question 7.
In a ∆ABC, DE is parallel to the base BC, with D on AB and E on AC. If \(\frac { AD }{ DB } =\frac { 2 }{ 3 } ,\frac { BC }{ DE } \)
Solution:
In ∆ABC, DE || BC
D is on AB and E is on AC
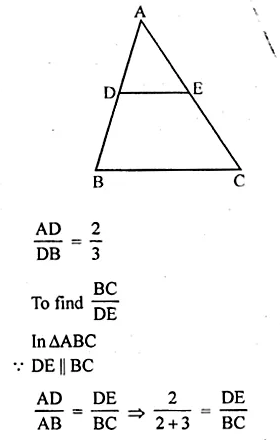
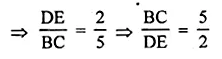
Question 8.
If the area of two similar triangles are 360 cm² and 250 cm² and if one side of the first triangle is 8 cm, find the length of the corresponding side of the second triangle.
Solution:
Let ∆ABC and ∆DEF are similar and area of
∆ABC = 360 cm²
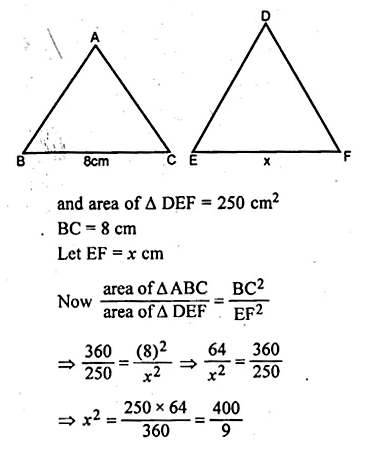
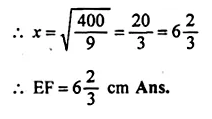
Question 9.
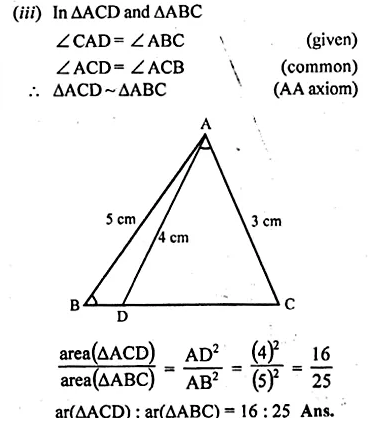
In the adjoining figure, D is a point on BC such that ∠ABD = ∠CAD. If AB = 5 cm, AC = 3 cm and AD = 4 cm, find
(i) BC
(ii) DC
(iii) area of ∆ACD : area of ∆BCA.
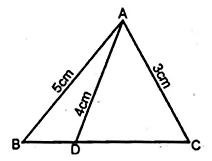
Solution:
In ∆ABC and ∆ACD
∠C = ∠C (Common)
∠ABC = ∠CAD (given)
∴ ∆ABC ~ ∆ACD

Question 10.
In the adjoining figure the diagonals of a parallelogram intersect at O. OE is drawn parallel to CB to meet AB at E, find area of DAOE : area of ||gm ABCD.
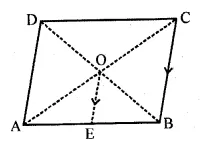
Solution:
(a) In the figure
Diagonals of parallelogram ABCD are
AC and BD which intersect each other at O.
OE is drawn parallel to CB to meet AB in E.


Question 11.
In the given figure, ABCD is a trapezium in which AB || DC. If 2AB = 3DC, find the ratio of the areas of ∆AOB and ∆COD.
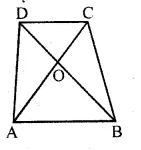
Solution:
In the given figure, ABCD is trapezium in
which AB || DC, 2AB = 3DC

Question 12.
In the adjoining figure, ABCD is a parallelogram. E is mid-point of BC. DE meets the diagonal AC at O and meet AB (produced) at F. Prove that .
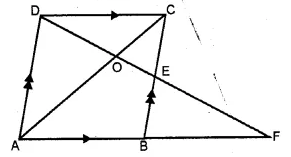
(i) DO : OE = 2 : 1
(ii) area of ∆OEC : area of ∆OAD = 1 : 4.
Solution:
Given : In || gm ABCD,
E is the midpoint of BC and DE meets the diagonal AC at O
and meet AB produced at F.
To prove : (i) DO : OE = 2 : 1
(ii) area of ∆OEC : area of ∆OAD = 1 : 4
Proof: In ∆AOD and ∆EDC
∠AOD = ∠EOC (vertically opposite angle)
∠OAD = ∠OCB (alt. angles)
∆AOD ~ ∆EOC (AA postulate)

Question 13.
A model of a ship is made to a scale of 1 : 250. Calculate :
(i) the length of the ship, if the length of model is 1.6 m.
(ii) the area of the deck of the ship, if the area of the deck of model is 2.4 m².
(iii) the volume of the model, if the volume of the ship is 1 km³.
Solution:
Scale factor (k) of the model of the ship = \(\\ \frac { 1 }{ 250 } \)
(i) Length of model = 1.6 m

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Chapter Test are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.