ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity MCQS
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity MCQS
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Chapter Test
Choose the correct answer from the given four options (1 to 22):
Question 1.
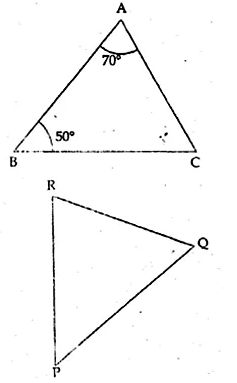
In the given figure, ∆ABC ~ ∆QPR. Then ∠R is
(a) 60°
(b) 50°
(c) 70°
(d) 80°
Solution:
In the given figure,
∆ABC ~ ∆QPR
∴ ∠A = ∠Q, ∠B = ∠P and ∠C = ∠R
But ∠A = 70°, ∠B = 50°
∴ ∠C = 180° – (70° + 500) = 180° – 120° = 60°
∠C = ∠R
∴ ∠R = ∠C = 60°
Question 2.
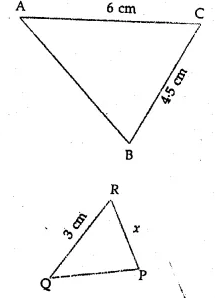
In the given figure, ∆ABC ~ ∆QPR. The value of x is
(a) 2.25 cm
(b) 4 cm
(c) 4.5 cm
(d) 5.2 cm
Solution:
In the given figure
∆ABC ~ ∆QPR
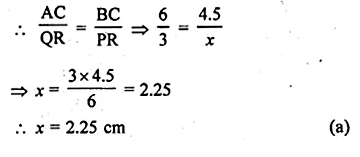
Question 3.
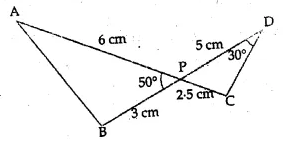
In the given figure, two line segments AC and BD intersect each other at the point P such that PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°. Then, ∠PBA is equal to
(a) 50°
(b) 30°
(c) 60°
(d) 100°
Solution:
In the given figure two line segments AC and BD intersect each other at P
and PA = 6 cm, PB = 3 cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°
In ∆APB and ∆CPD

Question 4.
If in two triangles ABC and PQR,
\(\frac { AB }{ QR } =\frac { BC }{ PR } =\frac { CA }{ PQ } \)
then
(a) ∆PQR ~ ∆CAB
(b) ∆PQR ~ ∆ABC
(c) ∆CBA ~ ∆PQR
(d) ∆BCA ~ ∆PQR
Solution:
In two ∆ABC and ∆PQR
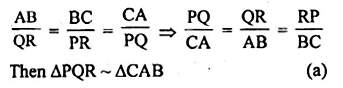
Question 5.
In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE, then the two triangles are
(a) congruent but not similar
(b) similar but not congruent
(c) neither congruent nor similar
(d) congruent as well as similar
Solution:
In ∆ABC and ∆DEF
∠B = ∠E, ∠F = ∠C
AB = 3DE
∵ Two angles of the one triangles are equal
to corresponding two angles of the other
But sides are not equal
∵ Triangles are similar but not congruent, (b)
Question 6.
In the given figure, if D, E and F are midpoints of the sides BC, CA and AB respectively, then the two triangles ABC and DEF are
(a) similar
(b) congruent
(c) both similar and congruent
(d) neither similar nor congruent
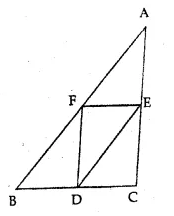
Solution:
D, E and F are the mid-points of the sides BC, CA and AB of ∆ABC
then two triangles ABC and DEF are similar. (a)
Question 7.
The given figure, AB || DE. The length of CD is
(a) 2.5 cm
(b) 2.7 cm
(c) \(\\ \frac { 10 }{ 3 } \) cm
(d) 3.5 cm
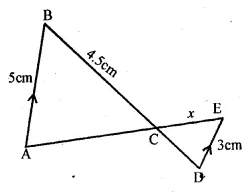
Solution:
In the given figure, AB || DE
∆ABC ~ ∆DCE
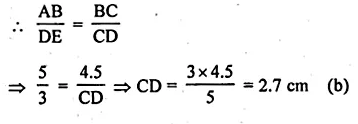
Question 8.
If in triangles ABC and DEF,\(\frac { AB }{ DE } =\frac { BC }{ FD } \) , then they will be similar when
(a) ∠B = ∠E
(b) ∠A = ∠D
(c) ∠B = ∠D
(d) ∠A = ∠F
Solution:
In two triangles ABC and DEF
\(\frac { AB }{ DE } =\frac { BC }{ FD } \)
They will be similar if their included angles are equal
∠B = ∠D (c)
Question 9.
If ∆PQR ~ ∆ABC, PQ = 6 cm, AB = 8 cm and perimeter of ∆ABC is 36 cm, then perimeter of ∆PQR is
(a) 20.25 cm
(b) 27 cm
(c) 48 cm
(d) 64 cm
Solution:
∆PQR ~ ∆ABC
PQ = 6 cm, AB = 8 cm
Perimeter of ∆ABC = 36 cm
Let perimeter of ∆PQR be x cm

Question 10.
In the given figure, DE || BC and all measurements are in centimetres. The length of AE is
(a) 2 cm
(b) 2.25 cm
(c) 3.5 cm
(d) 4 cm
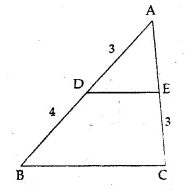
Solution:
In the given figure,
DE || BC
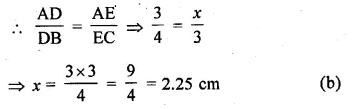
Question 11.
In the given figure, PQ || CA and all lengths are given in centimetres. The length of BC is
(a) 6.4 cm
(b) 7.5 cm
(c) 8 cm
(d) 9 cm
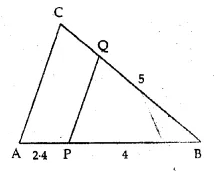
Solution:
In the given figure,
PQ || CA
Let BC = x

Question 12.
In the given figure, MN || QR. If PN = 3.6 cm, NR = 2.4 cm and PQ = 5 cm, then PM is
(a) 4 cm
(b) 3.6 cm
(c) 2 cm
(d) 3 cm
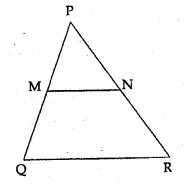
Solution:
In the given figure, MN || QR
PN = 3.6 cm, NR = 2.4 cm and PQ = 5 cm
Let PM = x cm

Question 13.
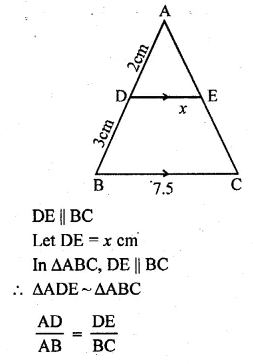
D and E are respectively the points on the sides AB and AC of a ∆ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC. Then the length of DE is
(a) 2.5 cm
(b) 3 cm
(c) 5 cm
(d) 6 cm
Solution:
D and E are the points on sides AB and AC of ∆ABC,
AD = 2 cm, BD = 3 cm,
BC = 7.5 cm
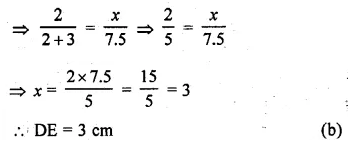
Question 14.
It is given that ∆ABC ~ ∆PQR with \(\frac { BC }{ QR } =\frac { 1 }{ 3 } \) then \(\frac { area\quad of\quad \Delta PQR }{ area\quad of\quad \Delta ABC } \) equal to
(a) 9
(b) 3
(c) \(\\ \frac { 1 }{ 3 } \)
(d) \(\\ \frac { 1 }{ 9 } \)
Solution:
∆ABC ~ ∆PQR
\(\frac { BC }{ QR } =\frac { 1 }{ 3 } \)
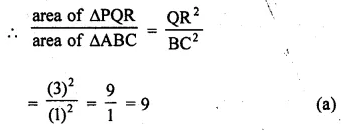
Question 15.
If the areas of two similar triangles are in the ratio 4 : 9, then their corresponding sides are in the ratio
(a) 9 : 4
(b) 3 : 2
(c) 2 : 3
(d) 16 : 81
Solution:
Ratio in the areas of two similar triangles = 4 : 9
Ratio in their corresponding sides
= √4 : √9
= 2 : 3 (c)
Question 16.
If ∆ABC ~ ∆PQR, BC = 8 cm and QR = 6 cm, then the ratio of the areas of ∆ABC and ∆PQR is
(a) 8 : 6
(b) 3 : 4
(c) 9 : 16
(d) 16 : 9
Solution:
∆ABC ~ ∆PQR, BC = 8 cm, QR = 6 cm
\(\frac { area\quad of\quad \Delta ABC }{ area\quad of\quad \Delta PQR } =\frac { { BC }^{ 2 } }{ { QR }^{ 2 } } \)
= \(\frac { { 8 }^{ 2 } }{ { 6 }^{ 2 } } =\frac { 64 }{ 36 } =\frac { 16 }{ 9 } \) (d)
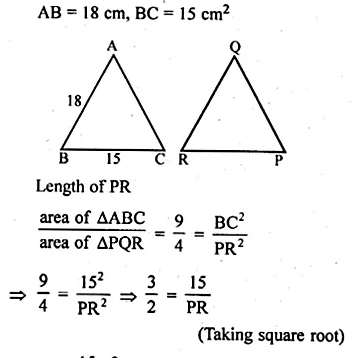
Question 17.
If ∆ABC ~ ∆QRP \(\frac { area\quad of\quad \Delta ABC }{ area\quad of\quad \Delta PQR } \) AB = 18 cm and BC = 15 cm, then the length of PR is equal to
(a) 10 cm
(b) 12 cm
(c) \(\\ \frac { 20 }{ 3 } \)
(d) 8 cm
Solution:
∆ABC ~ ∆QRP
\(\frac { area\quad of\quad \Delta ABC }{ area\quad of\quad \Delta PQR } \)

Question 18.
If ∆ABC ~ ∆PQR, area of ∆ABC = 81 cm², area of ∆PQR = 144 cm² and QR = 6 cm, then length of BC is
(a) 4 cm
(b) 4.5 cm
(c) 9 cm
(d) 12 cm
Solution:
∆ABC ~ ∆PQR,
area of ∆ABC = 81 cm² and area of ∆PQR = 144 cm²,
QR = 6 cm, BC = ?

Question 19.
In the given figure, DE || CA and D is a point on BD such that BD : DC = 2 : 1. The ratio of area of ∆ABC to area of ∆BDE is
(a) 4 : 1
(b) 9 : 1
(c) 9 : 4
(d) 3 : 2
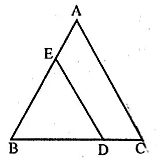
Solution:
In the given figure, DE || CA ,
D is a point on BC and BD : DC = 2 : 1
BD : BC = 2 : (2 + 1) = 2 : 3
In ∆ABC, DE || CA
∆ABC ~ ∆BDE
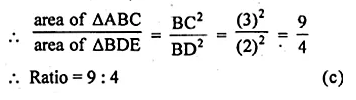
Question 20.
If ABC and BDE are two equilateral triangles such that D is mid-point of BC, then the ratio of the areas of triangles ABC and BDE is
(a) 2 : 1
(b) 1 : 2
(c) 1 : 4
(d) 4 : 1
Solution:
∆ABC and ∆BDE are an equilateral triangles
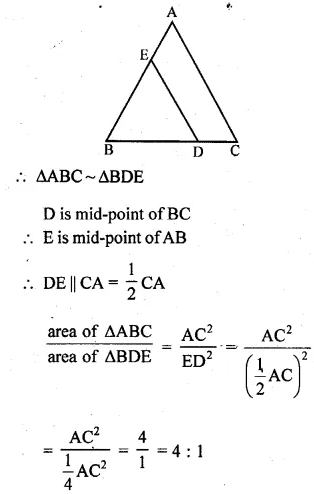
![]()
Question 21.
The areas of two similar triangles are 81 cm² and 49 cm² respectively. If an altitude of the smaller triangle is 3.5 cm, then the corresponding altitude of the bigger triangle is
(a) 9 cm
(b) 7 cm
(c) 6 cm
(d) 4.5 cm
Solution:
Areas of two similar triangles are 81 cm² and 49 cm²
The altitude of the smaller triangle is 3.5 cm
Let the altitude of the bigger triangle is x, then

Question 22.
Given ∆ABC ~ ∆PQR, area of ∆ABC = 54 cm² and area of ∆PQR = 24 cm². If AD and PM are medians of ∆’s ABC and PQR respectively, and length of PM is 10 cm, then length of AD is
(a) \(\\ \frac { 49 }{ 3 } \) cm
(b) \(\\ \frac { 20 }{ 3 } \) cm
(c) 15 cm
(d) 22.5 cm
Solution:
∆ABC ~ ∆PQR
area of ∆ABC = 54 cm²
and of ∆PQR = 24 cm²
AD and PM are their median respectively
PM = 10 cm
Let AD = x cm, then

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.