ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.3
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.3
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Chapter Test
Question 1.
Given that ∆s ABC and PQR are similar.
Find:
(i) The ratio of the area of ∆ABC to the area of ∆PQR if their corresponding sides are in the ratio 1 : 3.
(ii) the ratio of their corresponding sides if area of ∆ABC : area of ∆PQR = 25 : 36.
Solution:
(i) ∴ ∆ABC ~ ∆PQR
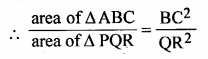
(By theorem 15.1)
But BC = QR =1 : 3
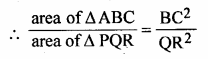

Question 2.
∆ABC ~ DEF. If area of ∆ABC = 9 sq. cm., area of ∆DEF =16 sq. cm and BC = 2.1 cm., find the length of EF.
Solution:
Let EF = x
Given that
∆ABC ~ ∆DEF,

Question 3.
∆ABC ~ ∆DEF. If BC = 3 cm, EF = 4 cm and area of ∆ABC = 54 sq. cm. Determine the area of ∆DEF.
Solution:
∆ABC ~ ∆DEF
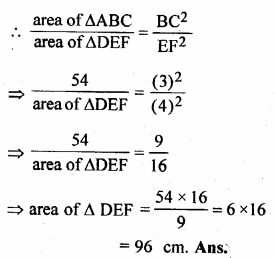
Question 4.
The area of two similar triangles are 36 cm² and 25 cm². If an altitude of the first triangle is 2.4 cm, find the corresponding altitude of the other triangle.
Solution:
Let ABC ~ ∆DEF, AL and DM are their altitudes
then area of ∆ABC = 36 cm²
area of ∆DEF = 25 cm² and AL = 2.4 cm.
Let DM = x
Now ∆ABC ~ ∆DEF

Question 5.
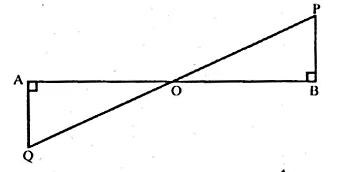
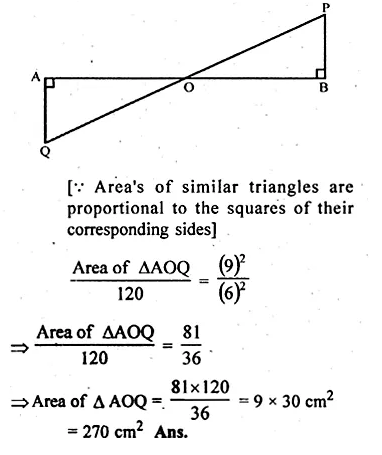
(a) In the figure, (i) given below, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and the area of ∆POB = 120 cm², find the area of ∆QOA. (2006)
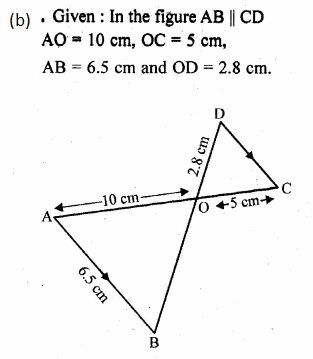
(b) In the figure (ii) given below, AB || DC. AO = 10 cm, OC = 5cm, AB = 6.5 cm and OD = 2.8 cm.
(i) Prove that ∆OAB ~ ∆OCD.
(ii) Find CD and OB.
(iii) Find the ratio of areas of ∆OAB and ∆OCD.
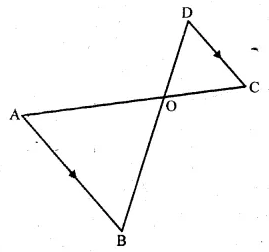
Solution:
In ∆AOQ and ∆BOP, we have
∠ OAQ = ∠ OBP [Each = 90°]
∠ AOQ= ∠BOP
[Vertically opposite angles]
∆AOQ ~ ∆BOP [A.A. similarity]
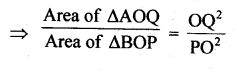


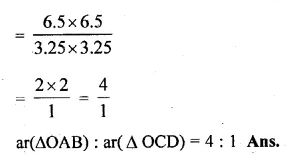
Question 6.
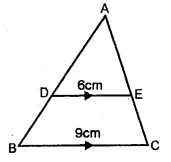
(a) In the figure (i) given below, DE || BC. If DE = 6 cm, BC = 9 cm and area of ∆ADE = 28 sq. cm, find the area of ∆ABC.
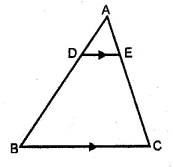
(b) In the figure (iii) given below, DE || BC and AD : DB = 1 : 2, find the ratio of the areas of ∆ADE and trapezium DBCE.
Solution:
(a) In the figure,
DE || BC
∠D = ∠B and ∠E = ∠C
(Corresponding angles)



Question 7.
In the given figure, DE || BC.
(i) Prove that ∆ADE and ∆ABC are similar.
(ii) Given that AD = \(\\ \frac { 1 }{ 2 } \) BD, calculate DE if BC = 4.5 cm.
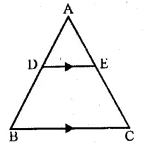
(iii) If area of ∆ABC = 18cm², find the area of trapezium DBCE
Solution:
(i) Given : In ∆ABC, DE || BC.
To prove : ∆ADE ~ ∆ABC
Proof: In ∆ADE and ∆ABC,
∠A = ∠A (common)
∠ADE = ∠ABC (corresponding angles)
∴ ∆ADE ~ ∆ABC. (AA axiom)
(ii) ∴ ∆ADE ~ ∆ABC
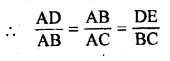



Question 8.
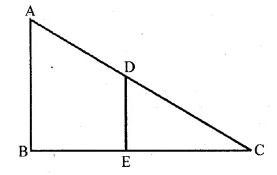
In the given figure, AB and DE are perpendicular to BC.
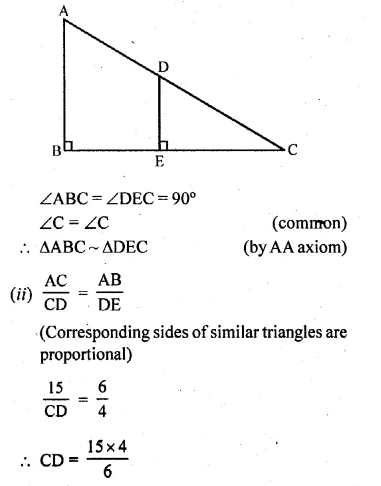
(i) Prove that ∆ABC ~ ∆DEC
(ii) If AB = 6 cm: DE = 4 cm and AC = 15 cm, calculate CD.
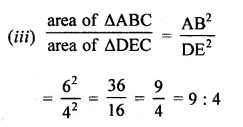
(iii) Find the ratio of the area of ∆ABC : area of ∆DEC.
Solution:
(i) To prove : ∆ABC ~ ∆DEC
In ∆ABC and ∆DEC
Question 9.
In the adjoining figure, ABC is a triangle.

(ii) Prove that ∆DEF is similar to ∆CBF.
Hence, find \(\\ \frac { EF }{ FB } \).
(iii) What is the ratio of the areas of ∆DEF and ∆CBF ? (2007)
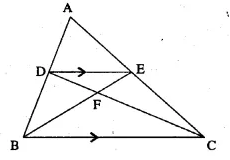
Solution:

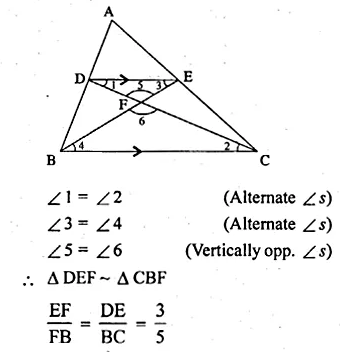

Question 10.
In ∆ABC, AP : PB = 2 : 3. PO is parallel to BC and is extended to Q so that CQ is parallel to BA. Find:
(i) area ∆APO : area ∆ABC.
(ii) area ∆APO : area ∆CQO. (2008)
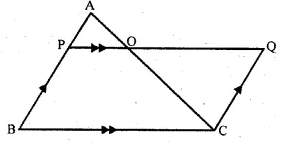
Solution:
In the figure,
PQ || BC and PO is produced to Q such that CQ || BA
and AP : PB = 2 : 3.
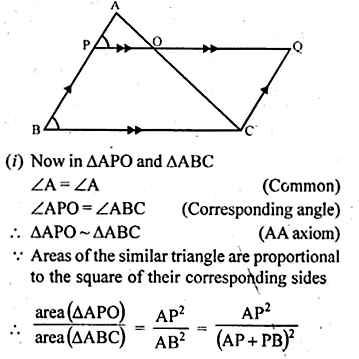

Question 11.
(a) In the figure (i) given below, ABCD is a trapezium in which AB || DC and AB = 2 CD. Determine the ratio of the areas of ∆AOB and ∆COD.
(b) In the figure (ii) given below, ABCD is a parallelogram. AM ⊥ DC and AN ⊥ CB. If AM = 6 cm, AN = 10 cm and the area of parallelogram ABCD is 45 cm², find
(i) AB
(ii) BC
(iii) area of ∆ADM : area of ∆ANB.
(c) In the figure (iii) given below, ABCD is a parallelogram. E is a point on AB, CE intersects the diagonal BD at O and EF || BC. If AE : EB = 2 : 3, find
(i) EF : AD
(ii) area of ∆BEF : area of ∆ABD
(iii) area of ∆ABD : area of trap. AFED
(iv) area of ∆FEO : area of ∆OBC.
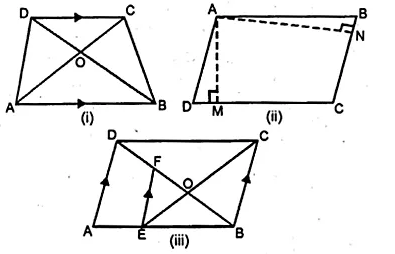
Solution:
(a) In trapezium ABCD, AB || DC.
∠OAB = ∠OCD [alternate angles]
∠OBA = ∠ODC
∆AOB ~ ∆COD





Question 12.
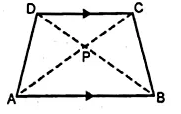
In the adjoining figure, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2 and DP produced meets AB produced at Q. If area of ∆CPQ = 20 cm², find
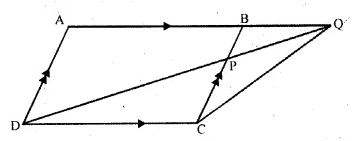
(i) area of ∆BPQ.
(ii) area ∆CDP.
(iii) area of || gm ABCD.
Solution:
In the figure, ABCD is a parallelogram.
P is a point on BC such that BP : PC = 1 : 2
and DP is produced to meet ABC produced at Q.
Area ∆CPQ = 20 cm²
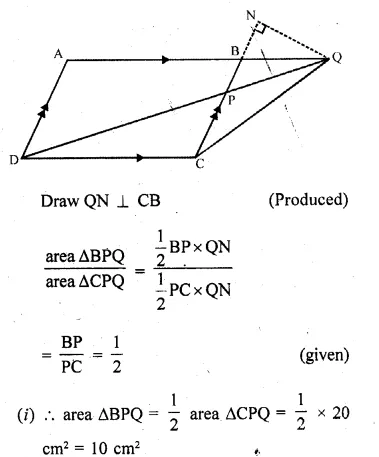


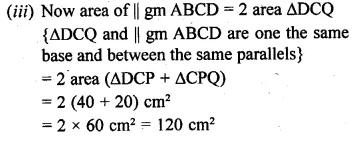
Question 13.
(a) In the figure (i) given below, DE || BC and the ratio of the areas of ∆ADE and trapezium DBCE is 4 : 5. Find the ratio of DE : BC.
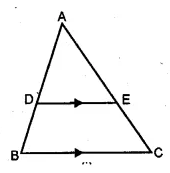
(b) In the figure (ii) given below, AB || DC and AB = 2 DC. If AD = 3 cm, BC = 4 cm and AD, BC produced meet at E, find (i) ED (ii) BE (iii) area of ∆EDC : area of trapezium ABCD.
Solution:
(a) In ∆ABC, DE || BC
Now in ∆ABC and ∆ADE
∠A = ∠A (common)
∠D = ∠B and ∠E = ∠C
(Corresponding angles)
∆ADE ~ ∆ABC




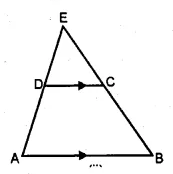
Question 14.
(a) In the figure given below, ABCD is a trapezium in which DC is parallel to AB. If AB = 9 cm, DC = 6 cm and BB = 12 cm., find
(i) BP
(ii) the ratio of areas of ∆APB and ∆DPC.
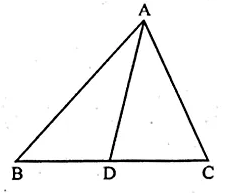
(b) In the figure given below, ∠ABC = ∠DAC and AB = 8 cm, AC = 4 cm, AD = 5 cm.
(i) Prove that ∆ACD is similar to ∆BCA
(ii) Find BC and CD
(iii) Find the area of ∆ACD : area of ∆ABC.
Solution:
(a) In trapezium ABCD, DC || AB
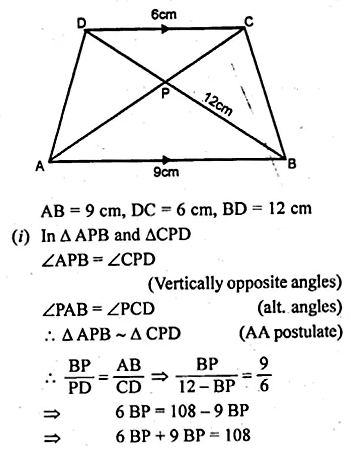
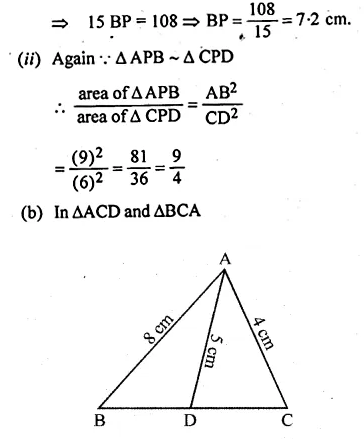

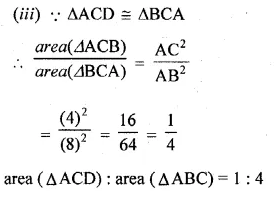
Question 15.
ABC is a right angled triangle with ∠ABC = 90°. D is any point on AB and DE is perpendicular to AC. Prove that:
(i) ∆ADE ~ ∆ACB.
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
(iii) Find, area of ∆ADE : area of quadrilateral BCED.
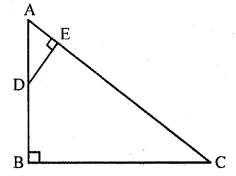
Solution:
(i) Consider DADE and DACB
∠A = ∠A (Common)
m∠B = m∠E = 90°
Thus by angle-angle similarity, triangles,
∆ACB ~ ∆ADE
(ii) Consider ∆ADE and ∆ACB
Since they are similar triangles,
the sides are proportional Thus, we have,



Question 16.
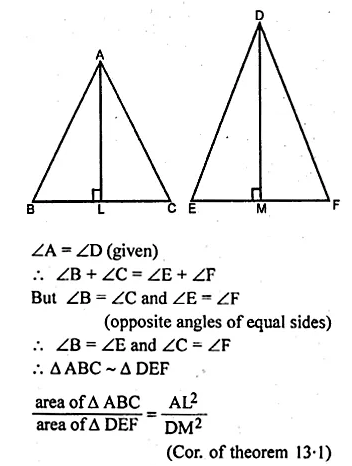
Two isosceles triangles have equal vertical angles and their areas are in the ratio 7 : 16. Find the ratio of their corresponding height.
Solution:
In two isosceles ∆s ABC and DEF
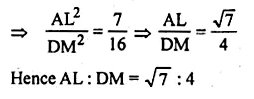
Question 17.
On a map drawn to a scale of 1 : 250000, a triangular plot of land has the following measurements :
AB = 3 cm, BC = 4 cm and ∠ABC = 90°. Calculate
(i) the actual length of AB in km.
(ii) the area of the plot in sq. km:
Solution:
Scale factor k = 1 : 250000 = \(\\ \frac { 1 }{ 250000 } \)
Length on map,
AB = 3 cm, BC = 4 cm

Question 18.
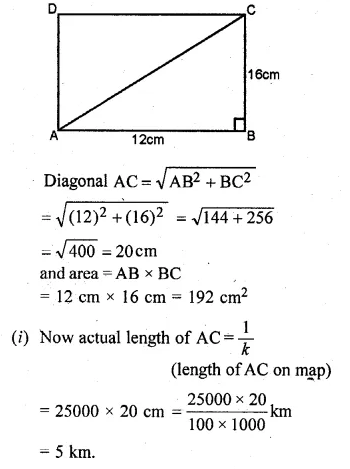
On a map drawn to a scale of 1 : 25000, a rectangular plot of land, ABCD has the following measurements AB = 12 cm and BG = 16 cm.
Calculate:
(i) the distance of a diagonal of the plot in km.
(ii) the area of the plot in sq. km.
Solution:
Scale factor (k) = \(\\ \frac { 1 }{ 25000 } \)
Measurements of plot ABCD on the map are
AB = 12 cm and BC = 16 cm.
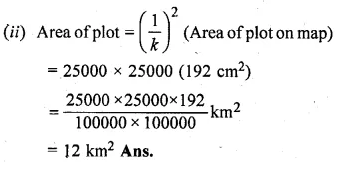
Question 19.
The model of a building is constructed with the scale factor 1 : 30.
(i) If the height of the model is 80 cm, find the actual height of the building in metres.
(ii) If the actual volume of a tank at the top of the building is 27 m³, find the volume of the tank on the top of the model. (2009)
Solution:
(i)


Question 20.
A model of a ship is made to a scale of 1 : 200.
(i) If the length of the model is 4 m, find the length of the ship.
(ii) If the area of the deck of the ship is 160000 m², find the area of the deck of the model.
(iii) If the volume of the model is 200 litres, find the volume of the ship in m³.
(100 litres = m³)
Solution:
Scale = 1 : 200
(i) Length of a model of ship = 4 m


Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.3 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.