ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.2
These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.2
More Exercises
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.1
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.2
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.3
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity MCQS
- ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Chapter Test
Question 1.
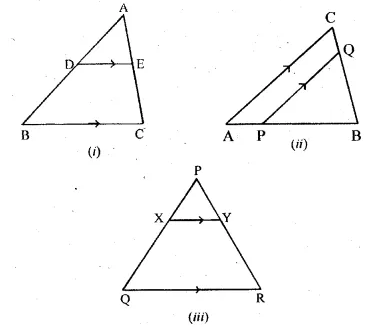
(a) In the figure (i) given below if DE || BG, AD = 3 cm, BD = 4 cm and BC = 5 cm. Find (i) AE : EC (ii) DE.
(b) In the figure (ii) given below, PQ || AC, AP = 4 cm, PB = 6 cm and BC = 8 cm. Find CQ and BQ.
(c) In the figure (iii) given below, if XY || QR, PX = 1 cm, QX = 3 cm, YR = 4.5 cm and QR = 9 cm, find PY and XY.
Solution:
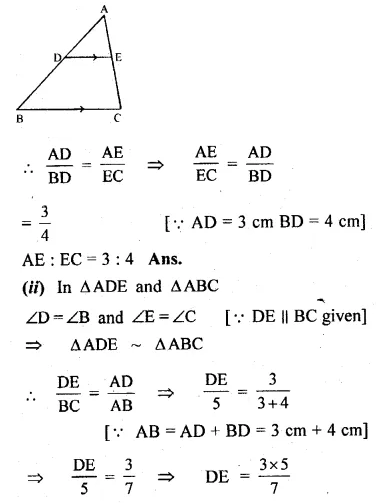
(a) In the figure (i)
Given : DE || BC, AD = 3 cm, BD = 4 cm and BC = 5 cm.
To find (i) AE : EC and
(ii) DE Since DE || BC of ∆ABC


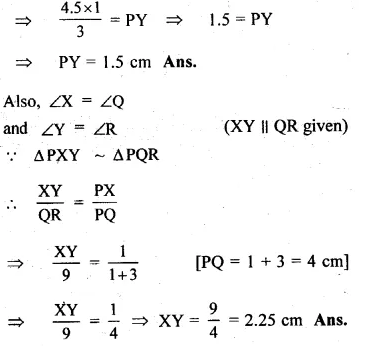
Question 2.
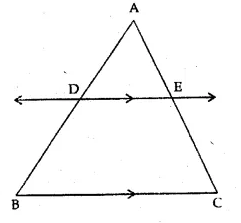
In the given figure, DE || BC.
(i) If AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, find the value of x.
(ii) If DB = x – 3, AB = 2x, EC = x – 2 and AC = 2x + 3, find the value of x.
Solution:
In the given figure, DE || BC
(i) AD = x, DB = x – 2, AE = x + 2, EC = x – 1
In ∆ABC,
∵DE || BC

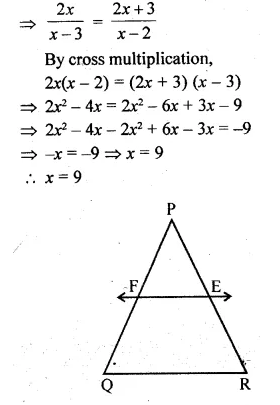
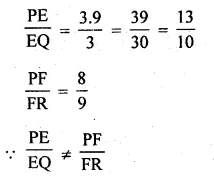
Question 3.
E and F are points on the sides PQ and PR respectively of a ∆PQR. For each of the following cases, state whether EF || QR:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 8 cm and RF = 9 cm.
(ii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm.
Solution:
(i) In ∆PQR, E and F are the points on the sides PQ and PR respectively
PE = 3.9 cm, EQ = 3 cm, PF = 8 cm,
RF = 9 cm
Is EF || QR ?
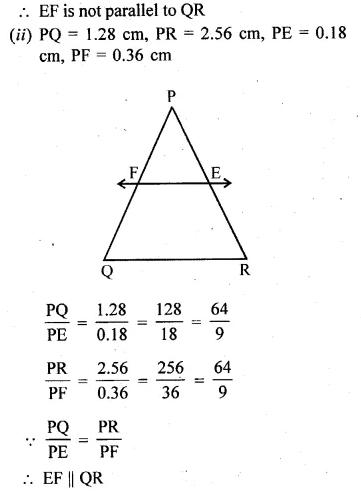
Question 4.
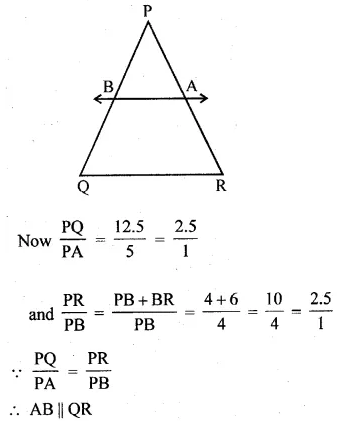
A and B are respectively the points on the sides PQ and PR of a triangle PQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm. Is AB || QR? Give reasons for your answer.
Solution:
In ∆PQR, A and B are points on the sides PQ and PR such that
PQ = 12.5 cm, PA = 5 cm, BR = 6 cm and PB = 4 cm
Question 5.
(a) In figure (i) given below, DE || BC and BD = CE. Prove that ABC is an isosceles triangle.
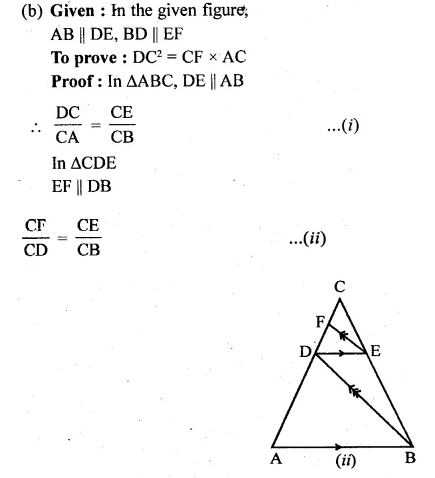
(b) In figure (ii) given below, AB || DE and BD || EF. Prove that DC² = CF x AC.
Solution:
(a) Given: In the figure,
DE || BC and BD = CE
To prove: ∆ABC is an isosceles triangle
Proof: In ∆ABC, DE || BC
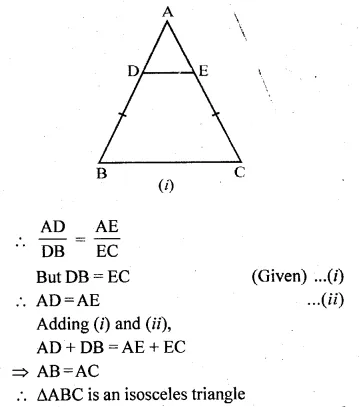

Question 6.
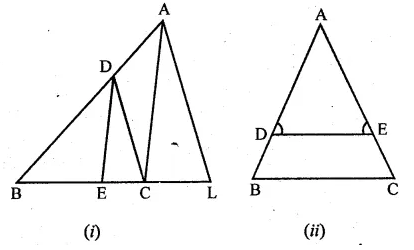
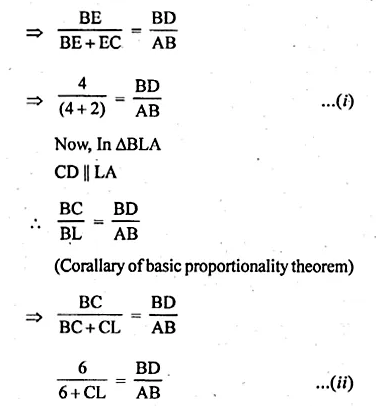
(a) In the figure (i) given below, CD || LA and DE || AC. Find the length of CL if BE = 4 cm and EC = 2 cm.
(b) In the given figure, ∠D = ∠E and \(\frac { AD }{ BD } =\frac { AE }{ EC } \). Prove that BAC is an isosceles triangle.
Solution:
(a) Given : CD || LA and DE || AC
Length of BE = 4 cm
Length of EC = 2 cm
Now, in ∆BCA
DE || AC
\(\frac { BE }{ BC } =\frac { BD }{ BA } \)
(Corallary of basic proportionality theorem)


Question 7.
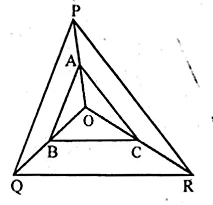
In the figure given below, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. show that BC || QR.
Solution:
In the given figure, A, B, C are points on
OP, OQ and OR respectively
and AB || PQ and AC || PR
To prove: BC || QR
Proof: In POQ,
AB || PQ

Question 8.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at O. Using Basic Proportionality theorem, prove that \(\frac { AO }{ BO } =\frac { CO }{ DO } \)
Solution:
Given : ABCD is a trapezium in which AB || DC
Its diagonals AC and BD intersect each other at O
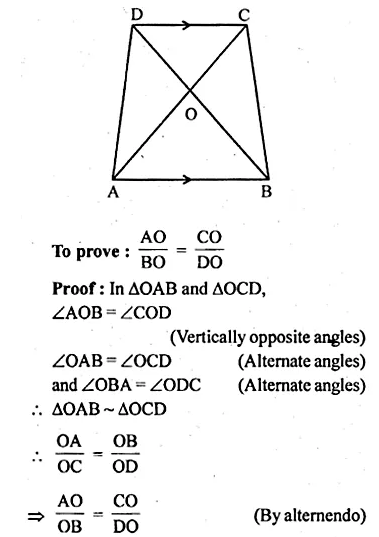
Question 9.
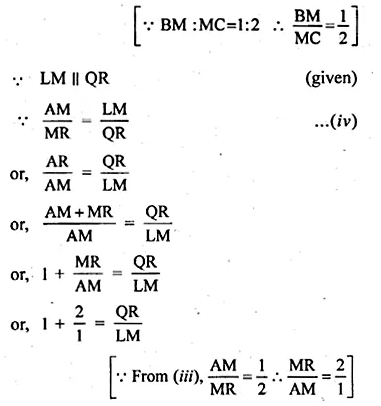
(a) In the figure (1) given below, AB || CR and LM || QR.
(i) Prove that \(\frac { BM }{ MC } =\frac { AL }{ LQ } \)
(ii) Calculate LM : QR, given that BM : MC = 1 : 2.
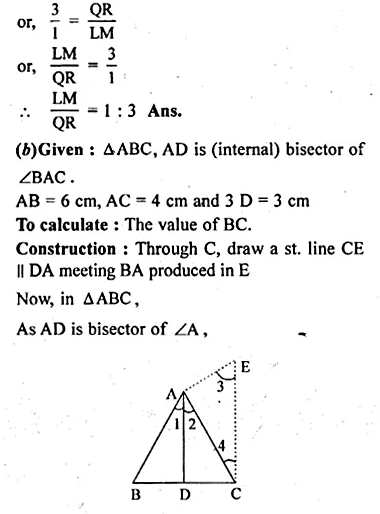
(b) In the figure (2) given below AD is bisector of ∠BAC. If AB = 6 cm, AC = 4 cm and BD = 3cm, find BC
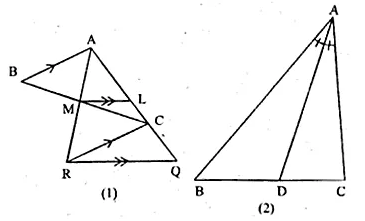
Solution:
(a) Given: AB || CR and LM II QR.
Also BM : MC = 1:2
To Prove:
(i) \(\frac { BM }{ MC } =\frac { AL }{ LQ } \)


Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 13 Similarity Ex 13.2 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.