RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
Other Exercises
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.1
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.2
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.3
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.4
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.5
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.6
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.7
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.10
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.12
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.13
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS
- RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations MCQS
Question 1.
The perimeter of a rectangular field is 82 m and its area is 400 m². Find the breadth of the rectangle.
Solution:
Perimeter of a rectangle field = 82 m
Length + Breadth = \(\frac { 82 }{ 2 }\) = 41 m
Let breadth = x m
Length = (41 – x) m
According to the condition,
Area = Length x breadth
400 = x (41 – x)
=> 400 = 4x – x²
=> x² – 41x + 400 = 0
=> x² – 16x – 25x + 400 = 0
=> x (x – 16) – 25 (x – 16) = 0
=> (x – 16) (x – 25) = 0
Either x – 16 = 0, then x = 16
or x – 25 = 0 then x = 25
25 > 16 and length > breadth
Breadth = 16 m
Question 2.
The length of a hall is 5 m more than its breadth. If the area of the floor of the hall is 84 m², what are the length and breadth of the hall ?
Solution:
Let breadth of the hall = x m
Then length = x + 5
Area of the floor = 84 m2
Now according to the condition,
x (x + 5) = 84
=> x² + 5x – 84 = 0
=> x² + 12x – 7x – 84 = 0
=> x (x + 12) – 7 (x + 12) = 0
=> (x + 12) (x – 7) = 0
Either x + 12 = 0, then x = -12 which is not possible being negative
or x – 7 = 0, then x = 7
Breadth of the hall = 7 m and length = 7 + 5 = 12 m
Question 3.
Two squares have sides x cm and (x + 4) cm. The sum of their areas is 656 cm². Find the sides of the squares.
Solution:
Side of first square = x cm
and side of the second square = (x + 4) cm
According to the condition,
x² + (x + 4)² = 656
=> x² + x² + 8x + 16 = 656
=> 2x² + 8x + 16 – 656 = 0
=> 2x² + 8x – 640 = 0
=> x² + 4x – 320 = 0 (Dividing by 2)
=> x² + 20x – 16x – 320 = 0
=> x (x + 20) – 16 (x + 20) 0
=> (x + 20) (x – 16) = 0
Either x + 20 = 0, then x = -20 which is not possible being negative
or x – 16 = 0, then x = 16
Side of first square = 16 cm
and side of second square = 16 + 4 = 20 cm
Question 4.
The area of a right angled triangle is 165 m². Determine its base and altitude if the latter exceeds the former by 7 m.
Solution:
Area of a right angled triangle = 165 m²
Let its base = x m
Then altitude = (x + 7) m
According to the condition,
\(\frac { 1 }{ 2 }\) x (x + 7) = 165
=> \(\frac { 1 }{ 2 }\) (x² + 7x) = 165
=> x² + 7x = 330
=> x² + 7x – 330 = 0
=> x² + 22x – 15x – 330 = 0
=> x (x + 22) – 15 (x + 22) = 0
=> (x + 22) (x – 15) = 0
Either x + 22 = 0, then x = -22 which is not possible being negative
or x – 15 = 0, then x = 15
Base = 15 m
and altitude = 15 + 7 = 22 m
Question 5.
Is it possible to design a rectangular mango grove whose length is twice its breadth and the area is 800 m² ? If so, find its length and breadth.
Solution:
Area of rectangular mango grove = 800 m²
Let breadth = x m
Then length = 2x m
According to the condition,
2x x x = 800
=> 2x² = 800
=> x² = 400 = (±20)²
Yes, it is possible,
x = 20, -20
But x = -20 is not possible being negative
Breadth = 20 m
and length = 20 x 2 = 40 m
Question 6.
Is it possible to design a rectangular park of perimeter 80 m and area 400 m² ? If so, find its length and breadth:
Solution:
Perimeter of rectangular park = 80 m
Length + Breadth = \(\frac { 80 }{ 2 }\) = 40 m
Let length = x m
Them breadth = 40 – x
According to the condition,
Area = Length x Breadth
x (40 – x) = 400
=> 40x – x² = 400
=> x² – 40x + 400 = 0
=> (x – 20)² = 0
=> x – 20 = 0
=> x = 20
Yes, it is possible
Length = 20 m
and breadth = 40 – x = 40 – 20 = 20 m
Question 7.
Sum of the areas of two squares is 640 m². If the difference of their perimeters is 64 m, find the sides of the two squares. [CBSE 2008]
Solution:
Let side of first square = x m
and of second squares = y m
According to the given conditions,
4x – 4y = 64
=> x – y = 16 ….(i)
and x² + y² = 640 ….(ii)
From (i), x = 16 + y
In (ii)
(16 + y)² + y² = 640
=> 256 + 32y + y² + y² = 640
=> 2y² + 32y + 256 – 640 = 0
=> y² + 16y – 192 = 0 (Dividing by 2)
=> y² + 24y – 8y – 192 = 0
=> y (y + 24) – 8 (y + 24) = 0
=> (y + 24)(y – 8) = 0
Either y + 24 = 0, then y = -24, which is not possible as it is negative
or y – 8 = 0, then y = 8
x = 16 + y = 16 + 8 = 24
Side of first square = 24 m
and side of second square = 8m
Question 8.
Sum of the areas of two squares is 400 cm². If the difference of their perimeters is 16 cm, find the sides of two squares. [CBSE 2013]
Solution:
Let perimeter of the first square = x cm
Then perimeter of second square = (x + 16) cm
Side of first square = \(\frac { x }{ 4 }\) cm
and side of second square = (\(\frac { x }{ 4 }\) + 4) cm
Sum of areas of these two squares = 400 cm²
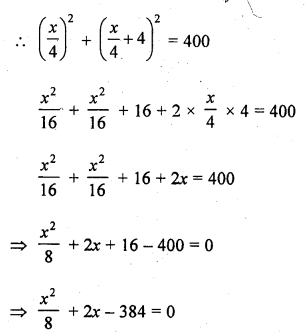

Question 9.
The area of a rectangular plot is 528 m². The length of the plot (in metres) is one metre more then twice its breadth. Find the length and the breadth of the plot. [CBSE 2014]
Solution:
Area of a rectangular plot = 528 m²
Let breadth = x m
Then length = (2x + 1) m
x (2x + 1) = 528 (∴ Area = l x b)
2x² + x – 528 = 0
=> 2x² + 33x – 32x² – 528 = 0
=> x (2x + 33) – 16 (2x + 33) = 0
=> (2x + 33) (x – 16) = 0
Either 2x + 33 = 0 then 2x = – 33 => x = \(\frac { -33 }{ 2 }\) but it is not possible being negative
or x – 16 = 0, then x = 16
Length = 2x + 1 = 16 x 2 + 1 = 33 m
and breadth = x = 16 m
Question 10.
In the centre of a rectangular lawn of dimensions 50 m x 40 m, a rectangular pond has to be constructed so that the area of the grass surrounding the pond would be 1184 m². Find the length and breadth of the pond. [NCERT Exemplar]
Solution:
Given that a rectangular pond has to be constructed in the centre of a rectangular lawn of dimensions 50 m x 40 m. So, the distance between pond and lawn would be same around the pond. Say x m.
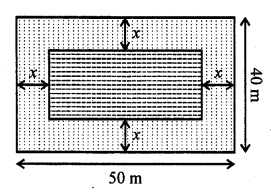
Now, length of rectangular lawn (l1) = 50 m
and breadth of rectangular lawn (b1) = 40 m
Length of rectangular pond (l2) = 50 – (x + x) = 50 – 2x
Also, area of the grass surrounding the pond = 1184 m²
Area of rectangular lawn – Area of rectangular pond = Area of grass surrounding the pond
l1 x b1 – l2 x b2= 1184 [∵ area of rectangle = length x breadth]
=> 50 x 40 – (50 – 2x) (40 – 2x) = 1184
=> 2000 – (2000 – 80x – 100x + 4x²) = 1184
=> 80x + 100x – 4x² = 1184
=> 4x² – 180x + 1184 = 0
=> x² – 45x + 296 = 0
=> x² – 21x – 8x + 296 = 0 [by splitting the middle term]
=> x (x – 37) – 8 (x – 37) = 0
=> (x – 37) (x – 8) = 0
∴ x = 8
[At x = 37, length and breadth, of pond are -24 and -34, respectively but length and breadth cannot be negative. So, x = 37 cannot be possible]
Length of pond = 50 – 2x = 50 – 2(8) = 50 – 16 = 34 m
and breadth of pond = 40 – 2x = 40 – 2(8) = 40 – 16 = 24 m
Hence, required length and .breadth of pond are 34 m and 24 m, respectively.
Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.11 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.