RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9

Other Exercises

Question 1.
Ashu is x years old while his mother Mrs. Veena is x² years old. Five years hence Mrs. Veena will be three times old as Ashu. Find their present ages.
Solution:
Present age of Ashu = x years
and age of his mother = x² years
5 years hence,
age of Ashu will be = (x + 5) years
and age of his mother = (x² + 5) years
According to the question,
x² + 5 = 3 (x + 5)
=> x² + 5 = 3x + 15
=> x² + 5 – 3x – 15 = 0
=> x² – 3x – 10 = 0
=> x² – 5x + 2x – 10 = 0
=> x (x – 5) + 2 (x – 5) = 0
=> (x – 5) (x + 2) = 0
Either x – 5 = 0, then x = 5
or x + 2 = 0, then x = -2 which is not possible being negative
Present age of Ashu = 5 years
and age of his mother = x² = (5)² = 25 years

Question 2.
The sum of the ages of a man and his son is 45 years. Five years ago, the product of their ages was four times the man’s age at that time. Find their present ages.
Solution:
Sum of ages of a man and his son = 45 years
Let the present age of the man = x years
Then age of his son = (45 – x) years
5 years ago,
Age of the man was = (x – 5) years
and age of his son = (45 – x – 5) years = (40 – x) years
According to the condition,
(x – 5) (40 – x) = 4 (x – 5)
=> 40 – x = 4 [Dividing by (x – 5)]
=> x = 40 – 4 = 36
Age of the man = 36 years
and age of his son = 45 – 36 = 9 years

Question 3.
The product of Shikha’s age five years ago and her age 8 years later is 30, her age at both times being given in years. Find her present age.
Solution:
Let present age of Shikha = x years
5 years ago, her age was = (x – 5) years
and 8 years later, her age will be = (x + 8) years
According to the condition,
(x – 5) (x + 8) = 30
=> x² + 3x – 40 = 30
=> x² + 3x – 40 – 30 = 0
=> x² + 3x – 70 = 0
=> x² + 10x – 7x – 70 = 0
=> x (x + 10) – 7 (x + 10) = 0
=> (x + 10)(x – 7) = 0
Either x + 10 = 0, then x = -10 which is not possible being negative
or x – 7 = 0, then x = 7
Her present age = 7 years

Question 4.
The product of Ramu’s age (in years) five years ago and his age (in years) nine years later is 15. Determine Ramu’s present age.
Solution:
Let present age of Ramu = x years
5 years ago his age was = (x – 5) years
and 9 years later his age will be = (x + 9) years
According to the condition,
(x – 5) (x + 9) = 15
=> x² + 9x – 5x – 45 = 15
=> x² + 4x – 45 – 15 = 0
=> x² + 4x – 60 = 0
=> x² + 10x – 6x – 60 = 0
=> x (x + 10) – 6 (x + 10) = 0
=> (x + 10) (x – 6) = 0
Either x + 10 = 0, then x = -10 but it is not possible being negative
or x – 6 = 0, then x = 6
Present age of Ramu = 6 years

Question 5.
Is the following situation possible? If so, determine their present ages. The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48.
Solution:
Sum of ages of two friends = 20 years
Let present age of one friend = x years
Age of second friend = (20 – x) years
4 years ago,
Age of first friend = x – 4
and age of second friend = 20 – x – 4 = 16 -x
According to the condition,
(x – 4) (16 – x) = 48
=> 16x – x² – 64 + 4x = 48
=> – x² + 20x – 64 – 48 = 0
=> – x² + 20x – 112 = 0
=> x² – 20x + 112 = 0
Here a = 1, b = – 20, c = 112
Discriminant(D) = b² – 4ac = (-20)² – 4 x 1 x 112
= 400 – 448 = – 48
∴ D < 0
Roots are not real
It is not possible

Question 6.
A girl is twice as old as her sister. Four years hence, the product of their ages (in years) will be 160. Find their present ages. [CBSE2010]
Solution:
Let age of sister = x years
Then age of girl = 2x years
4 years hence,
Girl’s age = 2x + 4
and sister’s age = x + 4
According to the condition,
(2x + 4) (x + 4) = 160
=> 2x² + 8x + 4x + 16 = 160
=> 2x² + 12x + 16 – 160 = 0
=> 2x²+ 12x – 144 = 0
=> x² + 6x – 12 = 0
=> x² + 12x – 6x – 72 = 0
=> x (x + 12) – 6 (x + 12) = 0
=> (x + 12) (x – 6) = 0
Either x + 12 = 0, then x = – 12 which is not possible being negative
or x – 6 = 0, then x = 6
Age of sister = 6 years
and age of girl = 2x = 2 x 6 = 12 years

Question 7.
The sum of the reciprocals of Rehman’s ages (in years) 3 years ago and 5 years from now is \(\frac { 1 }{ 3 }\). Find his present age. [NCERT]
Solution:
Let age of Rehman = x years
His age 3 years ago = x – 3
and age 5 years hence = x + 5
According to the condition,
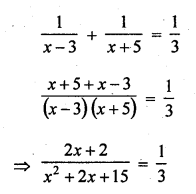
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9 1
=> x² + 2x – 15 = 6x + 6
=> x² + 2x – 15 – 6x – 6 = 0
=> x² – 4x – 21 =0
=> x² – 7x + 3x – 21 = 0
=> x (x – 7) + 3 (x – 7) = 0
=> (x – 7)(x + 3) = 0
Either x – 7 = 0, then x = 7
or x + 3 = 0 then x = – 3 which is not possible being negative
x = 7
His present age = 7 years

Question 8.
If Zeba were younger by 5 years than what she really is, then the square of her age (in years) would have been 11 more than 5 times her actual age. What is her age now? [NCERT Exemplar]
Solution:
Let the actual age of Zeba = x year .
Her age when she was 5 years younger = (x – 5) years
Now, by given condition,
Square of her age = 11 more than 5 times her actual age
(x – 5)² = 5 x actual age + 11
=> (x – 5)² = 5x + 11
=> x² + 25 – 10x = 5x + 11
=> x² – 15x + 14 = 0
=> x² – 14x – x + 14 = 0 [by splitting the middle term]
=> x (x – 14) – 1 (x – 14) = 0
=> (x – 1) (x – 14) = 0
=> x = 14
[Here, x ≠ 1 because her age is x – 5. So, x – 5 = 1 – 5= -4 i.e., age cannot be negative]
Hence, required Zeba’s age now is 14 years.

Question 9.
At present Asha’s age (in years) is 2 more than the square of her daughter Nisha’s age. When Nisha grows to her mother’s present age, Asha’s age would be one year less than 10 times the present age of Nisha. Find the present ages of both Asha and Nisha. [NCERT Exemplar]
Solution:
Let Nisha’s present age be x year.
Then, Asha’s present age = x² + 2 [by given condition]
Now, when Nisha grows to her mother’s present age i.e., after {(x² + 2) – x} years.
Then, Asha’s age also increased by [(x² + 2) – x] year.
Again by given condition,
Age of Asha = One years less than 10 times the present age of Nisha
(x² + 2) + {(x² + 2) – x} = 10x – 1
=> 2x² – x + 4 = 10x – 1
=> 2x² – 11x + 5 = 0
=> 2x² – 10x – x + 5 = 0
=> 2x (x – 5) – 1(x – 5) = 0
=> (x – 5) (2x – 1) = 0
∴ x = 5
[Here, x = \(\frac { 1 }{ 2 }\) cannot be possible, because at x = \(\frac { 1 }{ 2 }\), Asha’s age is 2\(\frac { 1 }{ 4 }\) years which is not possible]
Hence, required age of Nisha = 5 years
and required age of Asha = x² + 2 = (5)² + 2 = 25 + 2 = 27 years

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.9 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.