RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8

Other Exercises

Question 1.
The speed of a boat in still water is 8 km/hr. It can go 15 km upstream and 22 km downstream in 5 hours. Find the speed of the stream.
Solution:
Let the speed of stream = x km/h
and speed of boat in still water = 8 km/h
Distance covered up stream = 15 km
and downstream = 22 km
Total time taken = 5 hours
According to the conditions,
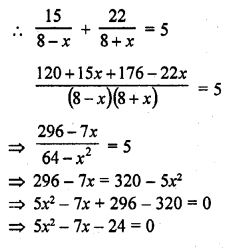
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 1

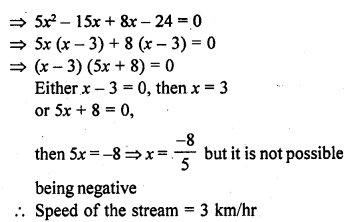
Question 2.
A train, travelling at a uniform speed for 360 km, would have taken 48 minutes less to travel the same distance if its speed were 5 km/hr more. Find the original speed of the train. [NCERT Exemplar]
Solution:
Let the original speed of the train = x km/h
Then, the increased speed of the train = (x + 5) km/h [by given condition]
and distance = 360 km
According to the question,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 3

Question 3.
A fast train takes one hour less than a slow train for a journey of 200 km. If the speed of the slow train is 10 km/hr less than that of the fast train, find the speed of the two trains.
Solution:
Total journey = 200 km
Let the speed of fast train = x km/hr
Then speed of slow train = (x – 10) km/hr
According to the condition,
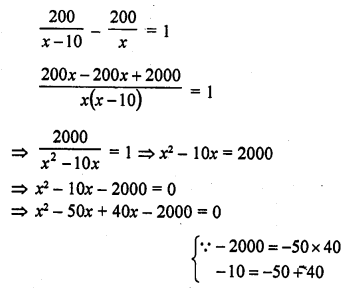
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 5
=> x (x – 50) + 40 (x – 50) = 0
=> (x – 50) (x + 40) = 0
Either x – 50 = 0, then x = 50
or x + 40 = 0, then x = -40 but it is not possible being negative
Speed of the fast train = 50 km/hr
and speed of the slow train = 50 – 40 = 10 km/hr

Question 4.
A passenger train takes one hour less for a journey of 150 km if its speed is increased by 5 km/hr from its usual speed. Find the usual speed of the train.
Solution:
Total journey = 150 km
Let the usual speed of the train = x km/hr
According to the condition,
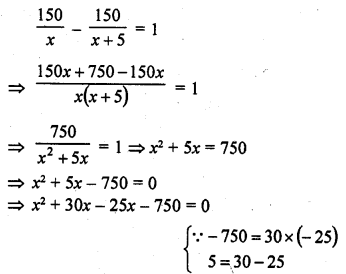
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 6
=> x (x + 30) – 25 (x + 30) = 0
=> (x + 30) (x – 25) = 0
Either x + 30 = 0, then x = -30 but it is not possible being negative
or x – 25 = 0, then x = 25
Usual speed of the train = 25 km/hr

Question 5.
The time taken by a person to cover 150 km was 2.5 hrs more than the time taken in the return journey. If he returned at a speed of 10 km/hr more than the speed of going, what was the speed per hour in each direction ?
Solution:
Distance = 150 km
Let the speed of the person while going = x km/hr
Then the speed while returning = (x + 10) km/hr
According to the condition,
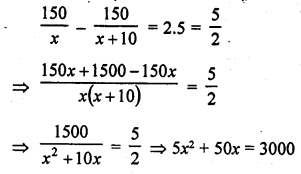
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 7

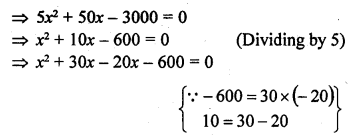
=> x (x + 30) – 20 (x + 30) = 0
=> (x + 30) (x – 20) = 0
Either x + 30 = 0, then x = -30 which is not possible being negative
or (x – 20) = 0 then x = 20
Usual speed of the man while going = 20 km/hr

Question 6.
A plane left 40 minutes late due to bad weather and in order to reach its destination, 1600 km away in time, it had to increase its speed by 400 km/hr from its usual speed. Find the usual speed of the plane.
Solution:
Distance = 1600 km
Let usual speed of the plane = x km/hr
Increased speed = (x + 400) km/hr
According to the condition,
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 9
is not possible being negative or x – 800 = 0, then x = 800
Usual speed of the plane = 800 km/hr

Question 7.
An aeroplane takes 1 hour less for a journey of 1200 km if its speed is increased by 100 km/hr from its usual speed. Find its usual speed.
Solution:
Distance = 1200 km
Let usual speed of the aeroplane = x km/hr
Increased speed = (x + 100) km/hr
According to the condition,
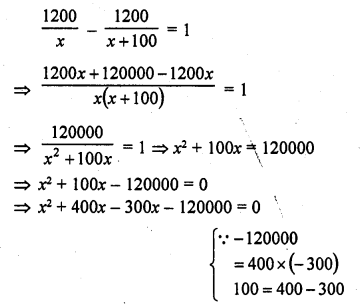
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 10
=> x (x + 400) – 300 (x + 400) = 0
=> (x + 400) (x – 300) = 0
Either x – 300 = 0, then x = 300
or x + 400 = 0, then x = -400 which is not possible being negative
Usual speed of the plane = 300 km/hr

Question 8.
A train travels at a certain average speed for a distance 63 km and then travels a distance of 72 km at an average speed of 6 km/hr more than the original speed. If it takes 3 hours to complete^total journey, what is its original average speed? [NCERT Exemplar]
Solution:
Let its original average speed be x km/h. Therefore
\(\frac { 63 }{ x }\) + \(\frac { 72 }{ x + 6 }\) = 3
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 11

Question 9.
A train covers a distance of 90 km at a uniform speed. Had the speed been 15 km/hr more, it would have taken 30 minutes less for the journey. Find the original speed of the train. [CBSE 2006C]
Solution:
Distance to be covered = 90 km
Let uniform-original speed = x km/h
Increased speed = (x + 15) km/hr
According to the condition,
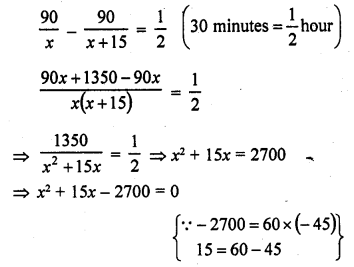
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 12
=> x² + 60x – 45x – 2700 = 0
=> x (x + 60) – 45 (x + 60) = 0
=> (x + 60)(x – 45) = 0
Either x + 60 = 0, then x = -60 which is not possible being negative
or x – 45 = 0, then x = 45
Original speed of the train = 45 km/hr

Question 10.
A train travels 360 km at a uniform speed. If the speed had been 5 km/hr more, it would have taken 1 hour less for the same journey. Find the speed of the train.
Solution:
Total distance = 360 km
Let uniform speed of the train = x km/hr
Increased speed = (x + 5) km/hr
According to the condition,
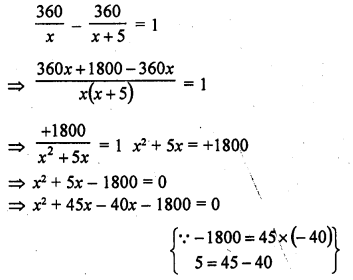
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 13
=> x (x + 45) – 40 (x + 45) = 0
=> (x + 45) (x – 40) = 0
Either x + 45 = 0, then x = -45 but it is not possible being negative
or x – 40 = 0, then x = 40
Speed of the train = 40 km/hr

Question 11.
An express train takes 1 hour less than a passenger train to travel 132 km between Mysore and Bangalore (without taking into consideration the time they stop at intermediate stations). If the average speed of the express train is 11 km/hr more than that of the passenger train, find the average speeds of the two trains.
Solution:
Distance between Mysore and Bangalore = 132 km
Let the speed of the passenger train=x km/hr
Then speed of express train = x + 11
According to the condition,
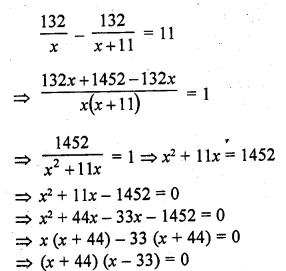
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 14
Either x + 44 = 0, then x = -44 but it is not possible being negative
or x – 33 = 0, then x = 33
Speed of passenger train = 33 km/hr
and speed of express train = 33 + 11 = 44 km/hr

Question 12.
An aeroplane left 50 minutes later than its scheduled time, and in order to reach the destination, 1250 km away, in time, it had to increase its speed by 250 km/hr from its usual speed. Find its usual speed. (CBSE 2010)
Solution:
Distance = 1250 km
Usual speed = x km/hr
Increased speed = (x + 250) km/hr
According to the condition,
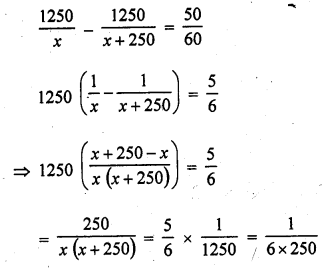
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 15

Question 13.
While boarding an aeroplane, a passenger got hurt. The pilot showing promptness and concern, made arrangements to hospitalise the injured and so the plane started late by 30 minutes to reach the destination, 1500 km away, in time, the pilot increased the speed by 100 km/hr. Find the original speed / hour of the plane. [CBSE 2013]
Solution:
Distance = 1500 km
Let the original speed of the aeroplane = x km/hr
Then increased speed = (x + 100) km/hr
According to the condition,
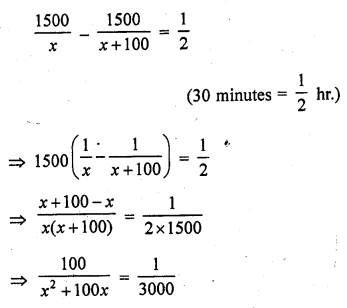
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 17
=> x² + 100x = 300000
=> x²+ 100x – 300000 = 0
=> x² + 600x – 500x – 300000 = 0
=> x (x + 600) – 500(x + 600) = 0
=> (x + 600) (x – 500) = 0
Either x + 600 = 0, then x = -600 which is not possible being negative
or x – 500 = 0, then x = 500
Original speed = 500 km/hr

Question 14.
A motorboat whose speed in still water is 18 km/h, takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream. [CBSE 2014]
Solution:
Let speed of the stream be x km/hr,
Speed of the boat upstream = (18 – x) km/hr
and Speed of the boat downstream = (18 + x) km/hr
Distance = 24 km
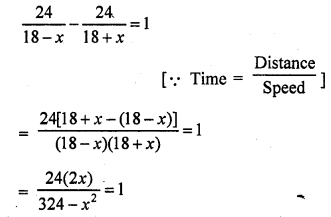
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 18
48x = 324 – x²
x² + 48x – 324 = 0
x² + 54x – 6x – 324 = 0
x(x + 54) – 6(x + 54) = 0
(x – 6) (x + 54) = 0
x – 6 = 0 or x + 54 = 0
x = 6 or x = – 54
Since speed cannot be negative
Speed of stream, x = 6 km/hr

Question 15.
A car moves a distance of 2592 km with uniform speed. The number of hours taken for the journey is one-half the number representing the speed, in km/ hour. Find the time taken to cover the distance. [CBSE 2017]
Solution:
Distance = 2592 km
Let the speed of the car = x km/hr
and time taken = \(\frac { x }{ 2 }\) hour
We have, Distance = Speed x Time
2592 = x x \(\frac { x }{ 2 }\)
=> 2592 = \(\frac { { x }^{ 2 } }{ 2 }\)
=> x² = 2592 x 2
=> x = √5184
=> x = 72 km/hr
and thus time taken = \(\frac { x }{ 2 }\) h = \(\frac { 72 }{ 2 }\) = 36 hour

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations Ex 4.8 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.