RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS

Other Exercises

Answer each of the following questions either in one word or one sentence or as per requirement of the question :
Question 1.
Write the value of k for which the quadratic equation x² – kx + 4 = 0 has equal roots.
Solution:
x² – kx + 4 = 0
Here a = 1, b = – k, c = 4
Discriminant (D) = b² – 4ac
= (-k)² – 4 x 1 x 4 = k² – 16
The roots are equal
D = 0 => k² – 16 = 0
=> (k + 4) (k – 4) = 0.
Either k + 4 = 0, then k = – 4
or k – 4 = 0, then k = 4
k = 4, -4

Question 2.
What is the nature of roots of the quadratic equation 4x² – 12x – 9 = 0 ?
Solution:
4x² – 12x – 9 = 0
Here a = 4, b = -12, c = – 9
Discriminant (D) = b² – 4ac = (-12)² – 4 x 4 x (-9)
= 144 + 144 = 288
D > 0
Roots are real and distinct

Question 3.
If 1 + √2 is a root of a quadratic equation with rational co-efficients, write its other root.
Solution:
The roots of the quadratic equation with rational co-efficients are conjugate
The other root will be 1 – √2

Question 4.
Write the number of real roots of the equation x² + 3 |x| + 2 = 0.
Solution:
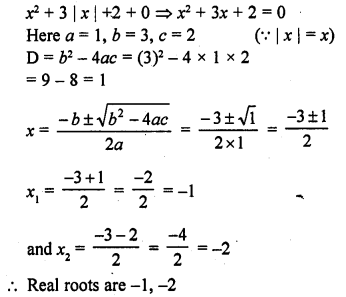
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS 1

Question 5.
Write the sum of the real roots of the equation x² + |x| – 6 = 0.
Solution:
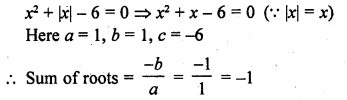
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS 2

Question 6.
Write the set of values of ‘a’ for which the equation x² + ax – 1 = 0, has real roots.
Solution:
x² + ax – 1=0
Here a = 1, b = a, c = -1
D = b² – 4ac = (a)² – 4 x 1 x (-1) = a² + 4
Roots are real
D ≥ 0 => a² + 4 ≥ 0
For all real values of a, the equation has real roots.

Question 7.
In there any real value of ‘a’ for which the equation x² + 2x + (a² + 1) = 0 has real roots ?
Solution:
x² + 2x + (a² + 1) = 0
D = (-b)² – 4ac = (2)² – 4 x 1 (a² + 1) = 4 – 4a² – 4 = – 4a²
For real value of x, D ≥ 0
But – 4a² ≤ 0
So it is not possible
There is no real value of a

Question 8.
Write the value of λ, for which x² + 4x + λ is a perfect square.
Solution:
In x² + 4x + λ
a = 1, b = 4, c = λ
x² + 4x + λ will be a perfect square if x² + 4x + λ = 0 has equal roots
D = b² – 4ac = (4)² – 4 x 1 x λ = 16 – 4λ
D = 0
=> 16 – 4λ = 0
=> 16 = 4A
=> λ = 4
Hence λ = 4

Question 9.
Write the condition to be satisfied for which equations ax² + 2bx + c = 0 and bx² – 2√ac x + b = 0 have equal roots.
Solution:
In ax² + 2bx + c = 0
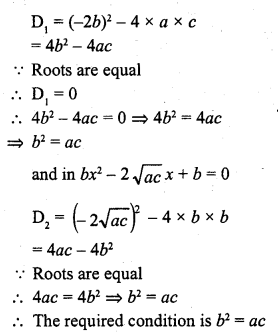
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS 3

Question 10.
Write the set of values of k for which the quadratic equation has 2x² + kx – 8 = 0 has real roots.
Solution:
In 2x² + kx – 8 = 0
D = b²- 4ac = (k)² – 4 x 2 x (-8) = k² + 64
The roots are real
D ≥ 0
k² + 64 ≥ 0
For all real values of k, the equation has real roots.

Question 11.
Write a quadratic polynomial, sum of whose zeros is 2√3 and their product is 2.
Solution:
Sum of zeros = 2√3
and product of zeros = 2
The required polynomial will be
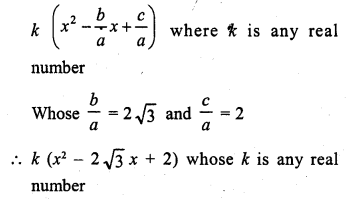
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS 4

Question 12.
Show that x = – 3 is a solution of x² + 6x + 9 = 0 (C.B.S.E. 2008)
Solution:
The given equation is x² + 6x + 9 = 0
If x = -3 is its solution then it will satisfy it
L.H.S. = (-3)² + 6 (-3) + 9 = 9 – 18 + 9 = 18 – 18 = 0 = R.H.S.
Hence x = – 3 is its one root (solution)

Question 13.
Show that x = – 2 is a solution of 3x² + 13x + 14 = 0. (C.B.S.E. 2008)
Solution:
The given equation is 3x² + 13x + 14 = 0
If x = – 2 is its solution, then it will satisfy it
L.H.S. = 3(-2)² + 13 (- 2) + 14 =3 x 4 – 26 + 14
= 12 – 26 + 14 = 26 – 26 = 0 = R.H.S.
Hence x = – 2 is its solution

Question 14.
Find the discriminant of the quadratic equation 3√3 x² + 10x + √3 =0. (C.B.S.E. 2009)
Solution:
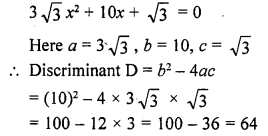
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS 5

Question 15.
If x = \(\frac { -1 }{ 2 }\), is a solution of the quadratic equation 3x² + 2kx – 3 = 0, find the value of k. [CBSE 2015]
Solution:
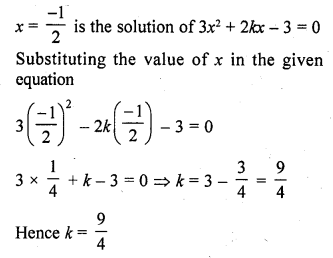
RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS 6

Hope given RD Sharma Class 10 Solutions Chapter 4 Quadratic Equations VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.