RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2

RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.1
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.3
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS

Question 1.
In the figure, OA and OB are opposite rays:
(i) If x = 25°, what is the value of y?
(ii) If y = 35°, what is the value of x?

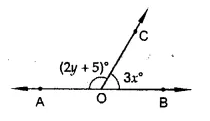
Solution:
(i) If x = 25°
∴ 3x = 3 x 25° = 75°
But ∠AOC + ∠BOC = 180° (Linear pair)
⇒ ∠AOC + 75° = 180°
⇒ ∠AOC = 180° – 75°
⇒ ∠AOC = 105°
∴ 2y + 5 = 105° ⇒ 2y= 105° – 5° = 100°
⇒ y = \(\frac { { 100 }^{ \circ } }{ 2 }\)  = 50°
∴ If x = 25° then y = 50°
(ii) If y = 35°, then ∠AOC = 2y + 5
∴ 2y + 5 = 2 x 35° + 5 = 70° + 5 = 75°
But ∠AOC + ∠BOC = 180° (Linear pair)
⇒ 75° + ∠BOC = 180°
⇒ ∠BOC = 180°-75°= 105°
∴ 3x = 105° ⇒ x = \(\frac { { 105 }^{ \circ } }{ 3 }\) = 35°
∴ x = 35°

Question 2.
In the figure, write all pairs of adjacent angles and all the linear pairs.

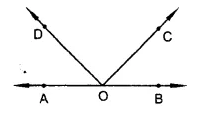
Solution:
In the given figure,
(i) ∠AOD, ∠COD; ∠BOC, ∠COD; ∠AOD, ∠BOD and ∠AOC, ∠BOC are the pairs of adjacent angles.
(ii) ∠AOD, ∠BOD and ∠AOC, ∠BOC are the pairs of linear pairs.

Question 3.
In the figure, find x, further find ∠BOC, ∠COD and ∠AOD.

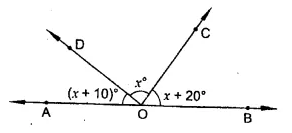
Solution:
In the figure,
AOB is a straight line
∴ ∠AOD + ∠DOB = 180° (Linear pair)
⇒ ∠AOD + ∠DOC + ∠COB = 180°
⇒ x+ 10° + x + x + 20 = 180°
⇒ 3x + 30° = 180°
⇒ 3x= 180° -30°= 150°
⇒ x = \(\frac { { 150 }^{ \circ } }{ 3 }\) = 50°
∴ x = 50°
Now ∠BOC =x + 20° = 50° + 20° = 70°
∠COD = x = 50°
and ∠AOD = x + 10° = 50° + 10° = 60°

Question 4.
In the figure, rays OA, OB, OC, OD and OE have the common end point O. Show that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.

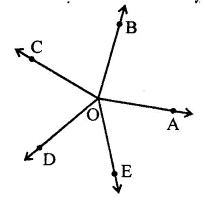
Solution:
Produce AO to F such that AOF is a straight line
Now ∠AOB + ∠BOF = 180° (Linear pair)

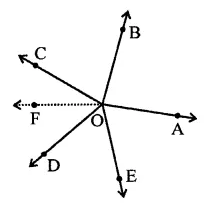
⇒ ∠AOB + ∠BOC + ∠COF = 180° …(i)
Similarly, ∠AOE + ∠EOF = 180°
⇒ ∠AOE + ∠EOD + ∠DOF = 180° …(ii)
Adding (i) and (ii)
∠AOB + ∠BOC + ∠COF + ∠DOF + ∠EOD + ∠AOE = 180° + 180°
⇒ ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°
Hence proved.

Question 5.
In the figure, ∠AOC and ∠BOC form a linear pair. If a – 2b = 30°, find a and b.

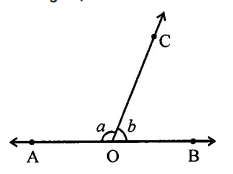
Solution:
∠AOC + ∠BOC = 180° (Linear pair)
⇒ a + 6 = 180° …(i)
and a – 2b = 30° …(ii)
Subtracting (ii) from (i), 3b = 150°
⇒ b = \(\frac { { 150 }^{ \circ } }{ 3 }\) = 50°
and a + 50° = 180°
⇒ a= 180°-50°= 130°
∴ a = 130°, b = 50°

Question 6.
How many pairs of adjacent angles are formed when two lines intersect in a point?
Solution:
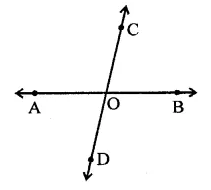
If two lines AB and CD intersect each other at a point O, then four pairs of linear pairs are formed i.e.
∠AOC, ∠BOC; ∠BOC, ∠BOD; ∠BOD, ∠AOD and ∠AOD, ∠AOC

Question 7.
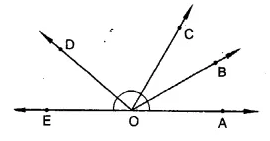
How many pairs of adjacent angles, in all, can you name in the figure.

Solution:
In the given figure 10 pairs of adjacent angles are formed as given below:
∠AOB, ∠BOC; ∠AOB, ∠BOD; ∠AOC, ∠COD; ∠AOD, ∠BOE; ∠AOB, ∠BOE; ∠AOC, ∠COF; ∠BOC, ∠COD; ∠BOC, ∠COE; ∠COD, ∠DOE and ∠BOD, ∠DOE

Question 8.
In the figure, determine the value of x.

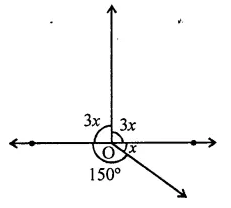
Solution:
In the figure
∠AOC + ∠COB + ∠BOD +∠AOD = 360 (angles at a point )

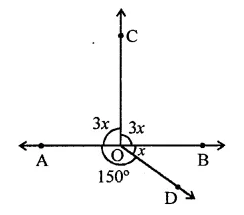
⇒ 3x + 3x + x + 150° = 360°
⇒ 7x – 360° – 150° = 210°
⇒ x = \(\frac { { 210 }^{ \circ } }{ 7 }\) = 30°
∴ x = 30°

Question 9.
In the figure, AOC is a line, find x.

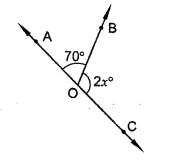
Solution:
In the figure,
∠AOB + ∠BOC = 180° (Linear pair)
⇒ 70° + 2x = 180°
⇒ 2x = 180° – 70°
⇒ 2x = 110°⇒x = \(\frac { { 110 }^{ \circ } }{ 2 }\) = 55°
∴ x = 55°

Question 10.
In the figure, POS is a line, find x.

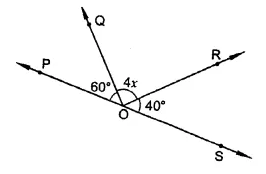
Solution:
In the figure, POS is a line
∴ ∠POQ + ∠QOS = 180° (Linear pair)
⇒ ∠POQ + ∠QOR + ∠ROS = 180°
⇒ 60° + 4x + 40° = 180°
⇒ 4x + 100° – 180°
⇒ 4x = 180° – 100° = 80°
⇒ x = \(\frac { { 80 }^{ \circ } }{ 4 }\) =20°
∴ x = 20°

Question 11.
In the figure, ACB is a line such that ∠DCA = 5x and ∠DCB = 4x. Find the value of x.

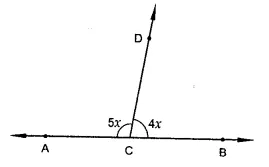
Solution:
ACB is a line, ∠DCA = 5x and ∠DCB = 4x
∠ACD + ∠DCB = 180° (Linear pair)
⇒ 5x + 4x = 180° ⇒ 9x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 9 }\) = 20°
∴ x = 20°
∴ ∠ACD = 5x = 5 x 20° = 100° and ∠DCB = 4x = 4 x 20° = 80°

Question 12.
Given ∠POR = 3x and ∠QOR = 2x + 10°, find the value ofx for which POQ will be a line.

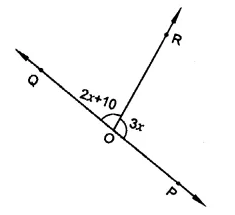
Solution:
∠POR = 3x and ∠QOR = 2x + 10°
If POQ is a line, then
∠POR + ∠QOR = 180° (Linear pair)
⇒ 3x + 2x + 10° = 180°
⇒ 5x = 180° – 10° = 170°
⇒ x = \(\frac { { 170 }^{ \circ } }{ 5 }\) = 34°
∴ x = 34°

Question 13.
What value ofy would make AOB, a line in the figure, if ∠AOC = 4y and ∠BOC = (6y + 30).

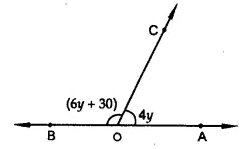
Solution:
In the figure,
AOB is a line if
∠AOC + ∠BOC = 180°
⇒ 6y + 30° + 4y= 180°
⇒ 10y= 180°-30°= 150°
150°
⇒ y = \(\frac { { 150 }^{ \circ } }{ 10 }\) = 15°
∴ y = 15°

Question 14.
In the figure, OP, OQ, OR and OS are four rays. Prove that: ∠POQ + ∠QOR + ∠SOR + ∠POS = 360° [NCERT]

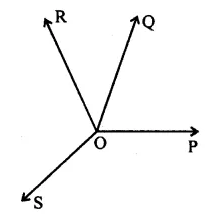
Solution:
In the figure, OP, OQ, OR and OS are the rays from O
To prove : ∠POQ + ∠QOR + ∠SOR + ∠POS = 360°
Construction : Produce PO to E

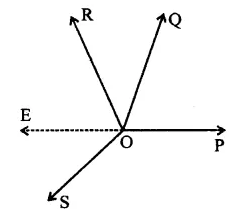
Proof: ∠POQ + ∠QOE = 180° (Linear pair)
Similarly, ∠EOS + ∠POS = 180°
Adding we get,
∠POQ + ∠QOR + ∠ROE + ∠EOS + ∠POS = 180° + 180° ,
⇒ ∠POQ + ∠QOR + ∠ROS + ∠POS = 360° Hence ∠POQ + ∠QOR + ∠SOR + ∠POS = 360°

Question 15.
In the figure, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ respectively. If ∠POS = x, find ∠ROT. [NCERT]

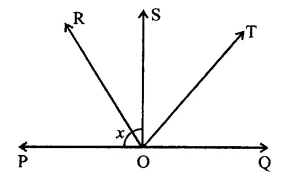
Solution:
Ray OR stands on a line POQ forming ∠POS and ∠QOS

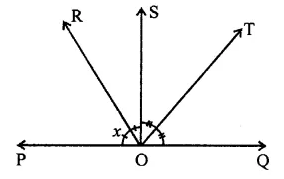
OR and OT the angle bisects of ∠POS and ∠QOS respectively. ∠POS = x
But ∠POS + ∠QOS = 180° (Linear pair)
⇒ x + ∠QOS = 180°
⇒ ∠QOS = 180° – x
∵ OR and OT are the bisectors of angle

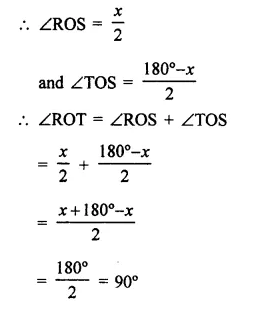
Question 16.
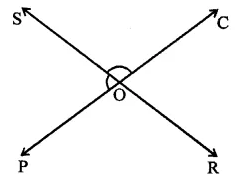
In the figure, lines PQ and RS intersect each other at point O. If ∠POR : ∠ROQ = 5 : 7. Find all the angles. [NCERT]

Solution:
Lines PQ and PR, intersect each other at O
∵ Vertically opposite angles are equal
∴ ∠POR = ∠QOS and ∠ROQ = ∠POS
∠POR : ∠ROQ = 5:7
Let ∠POR = 5x and ∠ROQ = 7x
But ∠POR + ∠ROQ = 180° (Linear pair)
∴ 5x + 7x = 180° ⇒ 12x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 12 }\) = 15°
∴ ∠POR = 5x = 5 x 15° = 75°
and ∠ROQ = 7x = 7 x 15° = 105°
But ∠QOS = POR = 75° (Vertically opposite angles)
and ∠POS = ∠ROQ = 105°

Question 17.
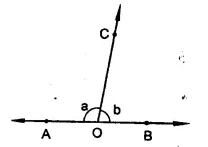
In the figure, a is greater than b by one third of a right-angle. Find the values of a and b.

Solution:
In the figure,
∠AOC + ∠BOC = 180° (Linear pair)
⇒ a + b =180° …(i)
But a = b + \(\frac { 1 }{ 3 }\) x 90° = b + 30°
⇒ a – b = 30° …(ii)
Adding (i) and (ii)
210°
2a = 210° ⇒ a = \(\frac { { 210 }^{ \circ } }{ 2 }\) = 105°
and 105° + b = 180°
⇒ b = 180° – 105°
∴ b = 75°
Hence a = 105°, b = 75°

Question 18.
In the figure, ∠AOF and ∠FOG form a linear pair.
∠EOB = ∠FOC = 90° and ∠DOC = ∠FOG = ∠AOB = 30°

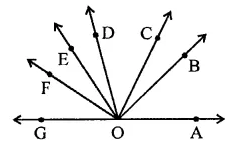
(i) Find the measures of ∠FOE, ∠COB and ∠DOE.
(ii) Name all the right angles.
(iii) Name three pairs of adjacent complementary angles.
(iv) Name three pairs of adjacent supplementary angles.
(v) Name three pairs of adjacent angles.
Solution:
In the figure,
∠AOF and ∠FOG form a linear pair
∠EOB = ∠FOC = 90°
∠DOC = ∠FOG = ∠AOB = 30°

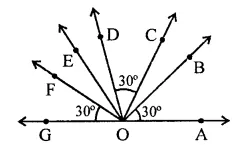
(i) ∠BOE = 90°, ∠AOB = 30°
But ∠BOE + ∠AOB + ∠EOG = 180°
⇒ 30° + 90° + ∠EOG = 180°
∴∠EOG = 180° – 30° – 90° = 60°
But ∠FOG = 30°
∴ ∠FOE = 60° – 30° = 30°
∠COD = 30°, ∠COF = 90°
∴ ∠DOF = 90° – 30° = 60°
∠DOE = ∠DOF – ∠EOF
= 60° – 30° = 30°
∠BOC = BOE – ∠COE
= 90° – 30° – 30° = 90° – 60° = 30°
(ii) Right angles are,
∠AOD = 30° + 30° + 30° = 90°
∠BOE = 30° + 30° + 30° = 90°
∠COF = 30° + 30° + 30° = 90°
and ∠DOG = 30° + 30° + 30° = 90°
(iii) Pairs of adjacent complementaiy angles are ∠AOB, ∠BOD; ∠AOC, ∠COD; ∠BOC, ∠COE
(iv) Pairs of adjacent supplementary angles are ∠AOB, ∠BOG; ∠AOC, ∠COG and ∠AOD, ∠DOG
(v) Pairs of adjacent angles are ∠BOC, ∠COD; ∠COD, ∠DOE and ∠DOE, ∠EOF.

Question 19.
In the figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = \(\frac { 1 }{ 2 }\)(∠QOS – ∠POS). [NCERT]

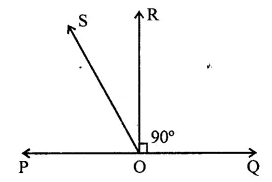
Solution:
Ray OR ⊥ ROQ. OS is another ray lying between OP and OR.

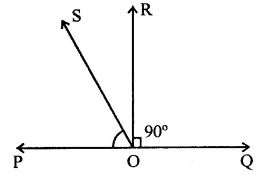
To prove : ∠ROS = \(\frac { 1 }{ 2 }\)(∠QOS – ∠POS)
Proof : ∵ RO ⊥ POQ
∴ ∠POR = 90°
⇒ ∠POS + ∠ROS = 90° …(i)
⇒ ∠ROS = 90° – ∠POS
But ∠POS + ∠QOS = 180° (Linear pair)
= 2(∠POS + ∠ROS) [From (i)]
∠POS + ∠QOS = 2∠ROS + 2∠POS
⇒ 2∠ROS = ∠POS + ∠QOS – 2∠POS
= ∠QOS – ∠POS
∴ ROS = \(\frac { 1 }{ 2 }\) (∠QOS – ∠POS)

Hope given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.