RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4

RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4

Other Exercises

• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.1
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.2
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.3
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles MCQS

Question 1.
In the figure, AB || CD and ∠1 and ∠2 are in the ratio 3 : 2. Determine all angles from 1 to 8.

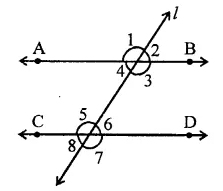
Solution:
AB || CD and l is transversal ∠1 : ∠2 = 3 : 2
Let ∠1 = 3x
Then ∠2 = 2x
But ∠1 + ∠2 = 180° (Linear pair)
∴ 3x + 2x = 180° ⇒ 5x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 5 }\)  = 36°
∴ ∠1 = 3x = 3 x 36° = 108°
∠2 = 2x = 2 x 36° = 72°
Now ∠1 = ∠3 and ∠2 = ∠4 (Vertically opposite angles)
∴ ∠3 = 108° and ∠4 = 72°
∠1 = ∠5 and ∠2 = ∠6 (Corresponding angles)
∴ ∠5 = 108°, ∠6 = 72°
Similarly, ∠4 = ∠8 and
∠3 = ∠7
∴ ∠8 = 72° and ∠7 = 108°
Hence, ∠1 = 108°, ∠2= 72°
∠3 = 108°, ∠4 = 72°
∠5 = 108°, ∠6 = 72°
∠7 = 108°, ∠8 = 12°

Question 2.
In the figure, l, m and n are parallel lines intersected by transversal p at X, Y and Z respectively. Find ∠l, ∠2 and ∠3.

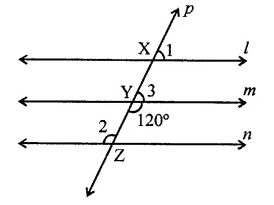
Solution:
l || m || n and p is then transversal which intersects then at X, Y and Z respectively ∠4 = 120°
∠2 = ∠4 (Alternate angles)
∴ ∠2 = 120°
But ∠3 + ∠4 = 180° (Linear pair)
⇒ ∠3 + 120° = 180°
⇒ ∠3 = 180° – 120°
∴ ∠3 = 60°
But ∠l = ∠3 (Corresponding angles)
∴ ∠l = 60°
Hence ∠l = 60°, ∠2 = 120°, ∠3 = 60°

Question 3.
In the figure, if AB || CD and CD || EF, find ∠ACE.

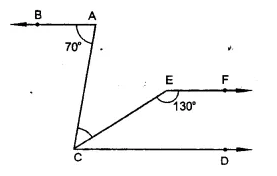
Solution:
Given : In the figure, AB || CD and CD || EF
∠BAC = 70°, ∠CEF = 130°
∵ EF || CD
∴ ∠ECD + ∠CEF = 180° (Co-interior angles)
⇒ ∠ECD + 130° = 180°
∴ ∠ECD = 180° – 130° = 50°
∵ BA || CD
∴ ∠BAC = ∠ACD (Alternate angles)
∴ ∠ACD = 70° (∵ ∠BAC = 70°)
∵ ∠ACE = ∠ACD – ∠ECD = 70° – 50° = 20°

Question 4.
In the figure, state which lines are parallel and why.

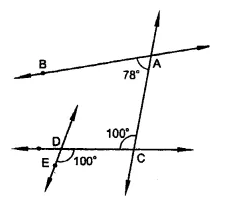
Solution:
In the figure,
∵ ∠ACD = ∠CDE = 100°
But they are alternate angles
∴ AC || DE

Question 5.
In the figure, if l || m,n|| p and ∠1 = 85°, find ∠2.

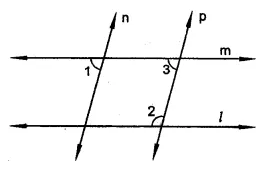
Solution:
In the figure, l || m, n|| p and ∠1 = 85°
∵ n || p
∴ ∠1 = ∠3 (Corresponding anlges)
But ∠1 = 85°
∴ ∠3 = 85°
∵ m || 1
∠3 + ∠2 = 180° (Sum of co-interior angles)
⇒ 85° + ∠2 = 180°
⇒ ∠2 = 180° – 85° = 95°

Question 6.
If two straight lines are perpendicular to the same line, prove that they are parallel to each other.
Solution:

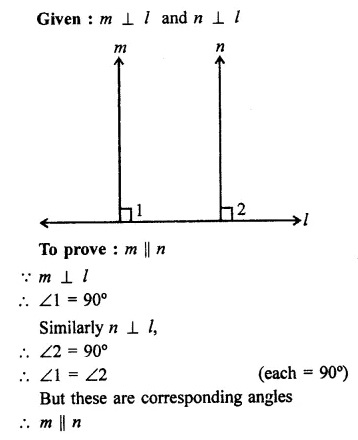
Question 7.
Two unequal angles of a parallelogram are in the ratio 2:3. Find all its angles in degrees.
Solution:
In ||gm ABCD,

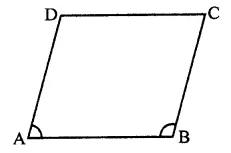
∠A and ∠B are unequal
and ∠A : ∠B = 2 : 3
Let ∠A = 2x, then
∠B = 3x
But ∠A + ∠B = 180° (Co-interior angles)
∴ 2x + 3x = 180°
⇒ 5x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 5 }\)  = 36°
∴ ∠A = 2x = 2 x 36° = 72°
∠B = 3x = 3 x 36° = 108°
But ∠A = ∠C and ∠B = ∠D (Opposite angles of a ||gm)
∴ ∠C = 72° and ∠D = 108°
Hence ∠A = 72°, ∠B = 108°, ∠C = 72°, ∠D = 108°

Question 8.
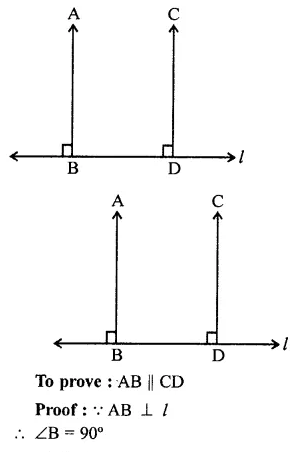
In each of the two lines is perpendicular to the same line, what kind of lines are they to each other?
Solution:
AB ⊥ line l and CD ⊥ line l

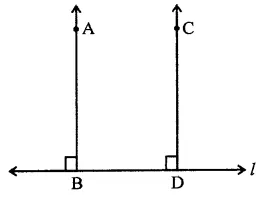
∴ ∠B = 90° and ∠D = 90°
∴ ∠B = ∠D
But there are corresponding angles
∴ AB || CD

Question 9.
In the figure, ∠1 = 60° and ∠2 = (\(\frac { 2 }{ 3 }\))3 a right angle. Prove that l || m.

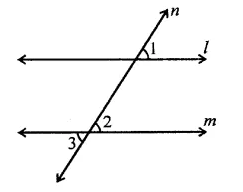
Solution:
In the figure, a transversal n intersects two lines l and m
∠1 = 60° and
∠2 = \(\frac { 2 }{ 3 }\) rd of a right angle 2
= \(\frac { 2 }{ 3 }\) x 90° = 60°
∴ ∠1 = ∠2
But there are corresponding angles
∴ l || m

Question 10.
In the figure, if l || m || n and ∠1 = 60°, find ∠2.

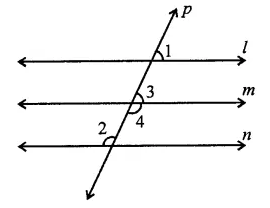
Solution:
In the figure,

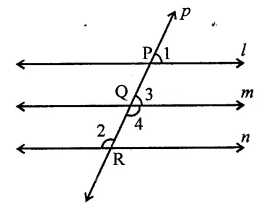
l || m || n and a transversal p, intersects them at P, Q and R respectively
∠1 = 60°
∴ ∠1 = ∠3 (Corresponding angles)
∴ ∠3 = 60°
But ∠3 + ∠4 = 180° (Linear pair)
60° + ∠4 = 180° ⇒ ∠4 = 180° – 60°
∴ ∠4 = 120°
But ∠2 = ∠4 (Alternate angles)
∴ ∠2 = 120°

Question 11.
Prove that the straight lines perpendicular to the same straight line are parallel to one another.
Solution:
Given : l is a line, AB ⊥ l and CD ⊥ l

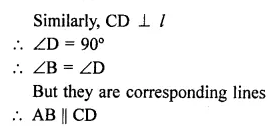
Question 12.
The opposite sides of a quadrilateral are parallel. If one angle of the quadrilateral is 60°, find the other angles.
Solution:
In quadrilateral ABCD, AB || DC and AD || BC and ∠A = 60°

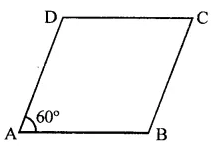
∵ AD || BC and AB || DC
∴ ABCD is a parallelogram
∴ ∠A + ∠B = 180° (Co-interior angles)
60° + ∠B = 180°
⇒ ∠B = 180°-60°= 120°
But ∠A = ∠C and ∠B = ∠D (Opposite angles of a ||gm)
∴ ∠C = 60° and ∠D = 120°
Hence ∠B = 120°, ∠C = 60° and ∠D = 120°

Question 13.
Two lines AB and CD intersect at O. If ∠AOC + ∠COB + ∠BOD = 270°, find the measure of ∠AOC, ∠COB, ∠BOD and ∠DOA.
Solution:
Two lines AB and CD intersect at O
and ∠AOC + ∠COB + ∠BOD = 270°
But ∠AOC + ∠COB + ∠BOD + ∠DOA = 360° (Angles at a point)

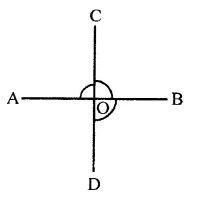
∴ 270° + ∠DOA = 360°
⇒ ∠DOA = 360° – 270° = 90°
But ∠DOA = ∠BOC (Vertically opposite angles)
∴ ∠BOC = 90°
But ∠DOA + ∠BOD = 180° (Linear pair)
⇒ 90° + ∠BOD = 180°
∴ ∠BOD= 180°-90° = 90° ,
But ∠BOD = ∠AOC (Vertically opposite angles)
∴ ∠AOC = 90°
Hence ∠AOC = 90°,
∠COB = 90°,
∠BOD = 90° and ∠DOA = 90°

Question 14.
In the figure, p is a transversal to lines m and n, ∠2 = 120° and ∠5 = 60°. Prove that m || n.

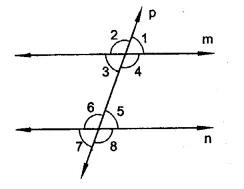
Solution:
Given : p is a transversal to the lines m and n
Forming ∠l, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8
∠2 = 120°, and ∠5 = 60°
To prove : m || n
Proof : ∠2 + ∠3 = 180° (Linear pair)
⇒ 120°+ ∠3 = 180°
⇒ ∠3 = 180°- 120° = 60°
But ∠5 = 60°
∴ ∠3 = ∠5
But there are alternate angles
∴ m || n

Question 15.
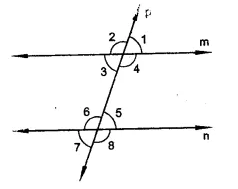
In the figure, transversal l, intersects two lines m and n, ∠4 = 110° and ∠7 = 65°. Is m || n?

Solution:
A transversal l, intersects two lines m and n, forming ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8
∠4 = 110° and ∠7 = 65°
To prove : Whether m || n or not
Proof : ∠4 = 110° and ∠7 = 65°
∠7 = ∠5 (Vertically opposite angles)
∴ ∠5 = 65°
Now ∠4 + ∠5 = 110° + 65° = 175°
∵ Sum of co-interior angles ∠4 and ∠5 is not 180°.
∴ m is not parallel to n

Question 16.
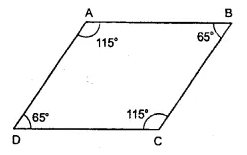
Which pair of lines in the figure are parallel? Give reasons.

Solution:
Given : In the figure, ∠A = 115°, ∠B = 65°, ∠C = 115° and ∠D = 65°
∵ ∠A + ∠B = 115°+ 65°= 180°
But these are co-interior angles,
∴ AD || BC
Similarly, ∠A + ∠D = 115° + 65° = 180°
∴ AB || DC

Question 17.
If l, m, n are three lines such that l ||m and n ⊥ l, prove that n ⊥ m.
Solution:
Given : l, m, n are three lines such that l || m and n ⊥ l

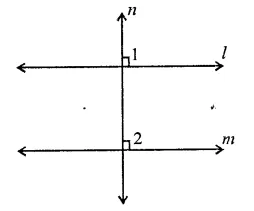
To prove : n ⊥ m
Proof : ∵ l || m and n is the transversal.
∴ ∠l = ∠2 (Corresponding angles)
But ∠1 = 90° (∵ n⊥l)
∴ ∠2 = 90°
∴ n ⊥ m

Question 18.
Which of the following statements are true (T) and which are false (F)? Give reasons.
(i) If two lines are intersected by a transversal, then corresponding angles are equal.
(ii) If two parallel lines are intersected by a transversal, then alternate interior angles are equal.
(iii) Two lines perpendicular to the same line are perpendicular to each other.
(iv) Two lines parallel to the same line are parallel to each other.
(v) If two parallel lines are intersected by a transversal, then the interior angles on the same side of the transversal are equal.
Solution:
(i) False. Because if lines are parallel, then it is possible.
(ii) True.
(iii) False. Not perpendicular but parallel to each other.
(iv) True.
(v) False. Sum of interior angles on the same side is 180° not are equal.

Question 19.
Fill in the blanks in each of the following to make the statement true:
(i) If two parallel lines are intersected by a transversal then each pair of corresponding angles are ……..
(ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are …….
(iii) Two lines perpendicular to the same line are ……… to each other.
(iv) Two lines parallel to the same line are ……… to each other.
(v) If a transversal intersects a pair of lines in such away that a pair of alternate angles are equal, then the lines are …….
(vi) If a transversal intersects a pair of lines in such away that the sum of interior angles on the same side of transversal is 180°, then the lines are …….
Solution:
(i) If two parallel lines are intersected by a transversal, then each pair of corresponding angles are equal.
(ii) If two parallel lines are intersected by a transversal, then interior angles on the same side of the transversal are supplementary.
(iii) Two lines perpendicular to the same line are parallel to each other.
(iv) Two lines parallel to the same line are parallel to each other.
(v) If a transversal intersects a pair of lines in such away that a pair of alternate angles are equal, then the lines are parallel.
(vi) If a transversal intersects a pair of lines in such away that the sum of interior angles on the same side of transversal is 180°, then the lines are parallel.

Question 20.
In the figure, AB || CD || EF and GH || KL. Find ∠HKL.

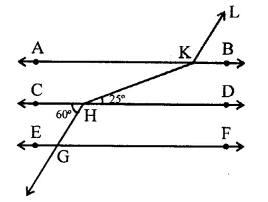
Solution:
In the figure, AB || CD || EF and KL || HG Produce LK and GH

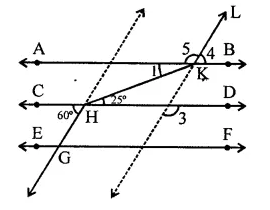
∵ AB || CD and HK is transversal
∴ ∠1 = 25° (Alternate angles)
∠3 = 60° (Corresponding angles)
and ∠3 = ∠4 (Corresponding angles)
= 60°
But ∠4 + ∠5 = 180° (Linear pair)
⇒ 60° + ∠5 = 180°
⇒ ∠5 = 180° – 60° = 120°
∴ ∠HKL = ∠1 + ∠5 = 25° + 120° = 145°

Question 21.
In the figure, show that AB || EF.

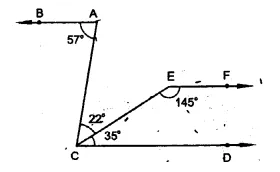
Solution:
Given : In the figure, AB || EF
∠BAC = 57°, ∠ACE = 22°
∠ECD = 35° and ∠CEF =145°
To prove : AB || EF,
Proof : ∠ECD + ∠CEF = 35° + 145°
= 180°
But these are co-interior angles
∴ EF || CD
But AB || CD
∴ AB || EF

Question 22.
In the figure, PQ || AB and PR || BC. If ∠QPR = 102°. Determine ∠ABC. Give reasons.

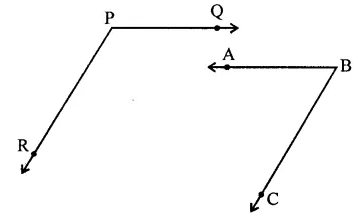
Solution:
In the figure, PQ || AB and PR || BC
∠QPR = 102°
Produce BA to meet PR at D

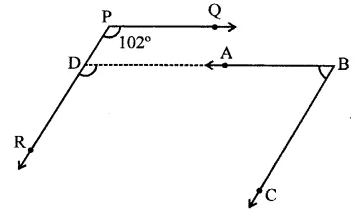
∵ PQ || AB or DB
∴ ∠QPR = ∠ADR (Corresponding angles)
∴∠ADR = 102° or ∠BDR = 102°
∵ PR || BC
∴ ∠BDR + ∠DBC = 180°
(Sum of co-interior angles) ⇒ 102° + ∠DBC = 180°
⇒ ∠DBC = 180° – 102° = 78°
⇒ ∠ABC = 78°

Question 23.
Prove that if the two arms of an angle are perpendicular to the two arms of another angle, then the angles are either equal or supplementary.
Solution:
Given : In two angles ∠ABC and ∠DEF AB ⊥ DE and BC ⊥ EF
To prove: ∠ABC + ∠DEF = 180° or ∠ABC = ∠DEF
Construction : Produce the sides DE and EF of ∠DEF, to meet the sides of ∠ABC at H and G.


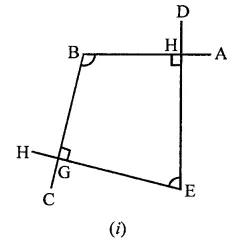
Proof: In figure (i) BGEH is a quadrilateral
∠BHE = 90° and ∠BGE = 90°
But sum of angles of a quadrilateral is 360°
∴ ∠HBG + ∠HEG = 360° – (90° + 90°)
= 360° – 180°= 180°
∴ ∠ABC and ∠DEF are supplementary
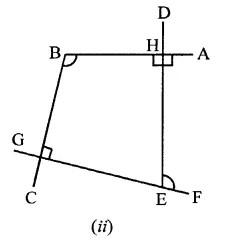
In figure (if) in quadrilateral BGEH,
∠BHE = 90° and ∠HEG = 90°
∴ ∠HBG + ∠HEG = 360° – (90° + 90°)
= 360°- 180° = 180° …(i)
But ∠HEF + ∠HEG = 180° …(ii) (Linear pair)
From (i) and (ii)
∴ ∠HEF = ∠HBG
⇒ ∠DEF = ∠ABC
Hence ∠ABC and ∠DEF are equal or supplementary

Question 24.
In the figure, lines AB and CD are parallel and P is any point as shown in the figure. Show that ∠ABP + ∠CDP = ∠DPB.

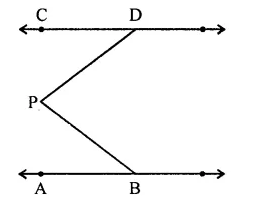
Solution:
Given : In the figure, AB || CD
P is a point between AB and CD PD
and PB are joined
To prove : ∠APB + ∠CDP = ∠DPB
Construction : Through P, draw PQ || AB or CD

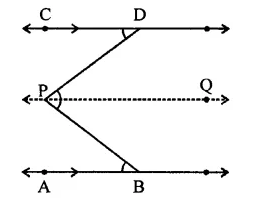
Proof: ∵ AB || PQ
∴ ∠ABP = BPQ …(i) (Alternate angles)
Similarly,
CD || PQ
∴ ∠CDP = ∠DPQ …(ii)
(Alternate angles)
Adding (i) and (ii)
∠ABP + ∠CDP = ∠BPQ + ∠DPQ
Hence ∠ABP + ∠CDP = ∠DPB

Question 25.
In the figure, AB || CD and P is any point shown in the figure. Prove that:
∠ABP + ∠BPD + ∠CDP = 360°

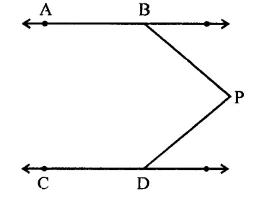
Solution:
Given : AB || CD and P is any point as shown in the figure
To prove : ∠ABP + ∠BPD + ∠CDP = 360°
Construction : Through P, draw PQ || AB and CD

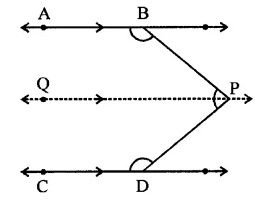
Proof : ∵ AB || PQ
∴ ∠ABP+ ∠BPQ= 180° ……(i) (Sum of co-interior angles)
Similarly, CD || PQ
∴ ∠QPD + ∠CDP = 180° …(ii)
Adding (i) and (ii)
∠ABP + ∠BPQ + ∠QPD + ∠CDP
= 180°+ 180° = 360°
⇒ ∠ABP + ∠BPD + ∠CDP = 360°

Question 26.
In the figure, arms BA and BC of ∠ABC are respectively parallel to arms ED and EF of ∠DEF. Prove that ∠ABC = ∠DEF.

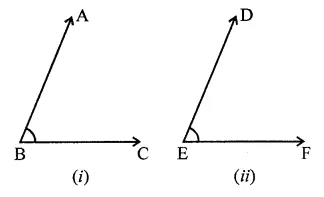
Solution:
Given : In ∠ABC and ∠DEF. Their arms are parallel such that BA || ED and BC || EF
To prove : ∠ABC = ∠DEF
Construction : Produce BC to meet DE at G
Proof: AB || DE
∴ ∠ABC = ∠DGH…(i) (Corresponding angles)

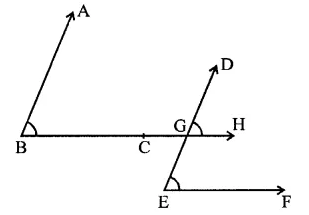
BC or BH || EF
∴ ∠DGH = ∠DEF (ii) (Corresponding angles)
From (i) and (ii)
∠ABC = ∠DEF

Question 27.
In the figure, arms BA and BC of ∠ABC are respectively parallel to arms ED and EF of ∠DEF. Prove that ∠ABC + ∠DEF = 180°.

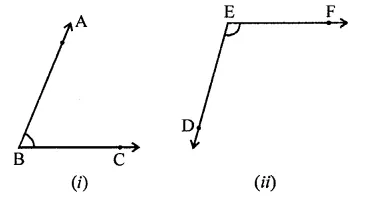
Solution:
Given: In ∠ABC = ∠DEF
BA || ED and BC || EF
To prove: ∠ABC = ∠DEF = 180°
Construction : Produce BC to H intersecting ED at G

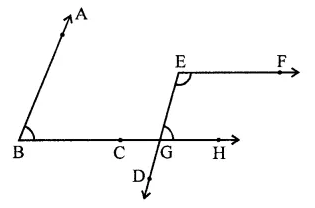
Proof: ∵ AB || ED
∴ ∠ABC = ∠EGH …(i) (Corresponding angles)
∵ BC or BH || EF
∠EGH || ∠DEF = 180° (Sum of co-interior angles)
⇒ ∠ABC + ∠DEF = 180° [From (i)]
Hence proved.

Hope given RD Sharma Class 9 Solutions Chapter 10 Congruent Triangles Ex 10.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.