RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2

Other Exercises

Question 1.
The exterior angles obtained on producing the base of a triangle both ways are 104° and 136°. Find all the angles of the triangle.
Solution:
In ∆ABC, base BC is produced both ways to D and E respectivley forming ∠ABE = 104° and ∠ACD = 136°
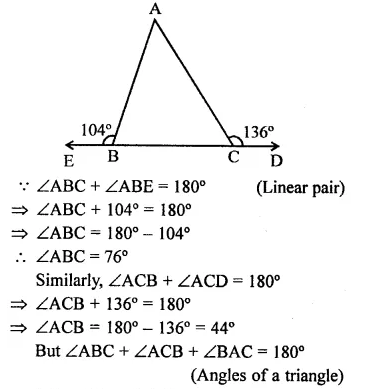
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q1.1

Question 2.
In the figure, the sides BC, CA and AB of a ∆ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the ∆ABC.
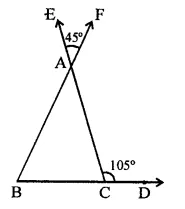
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q2.1
Solution:
In ∆ABC, sides BC, CA and BA are produced to D, E and F respectively.
∠ACD = 105° and ∠EAF = 45°
∠ACD + ∠ACB = 180° (Linear pair)
⇒ 105° + ∠ACB = 180°
⇒ ∠ACB = 180°- 105° = 75°
∠BAC = ∠EAF (Vertically opposite angles)
= 45°
But ∠BAC + ∠ABC + ∠ACB = 180°
⇒ 45° + ∠ABC + 75° = 180°
⇒ 120° +∠ABC = 180°
⇒ ∠ABC = 180°- 120°
∴ ∠ABC = 60°
Hence ∠ABC = 60°, ∠BCA = 75°
and ∠BAC = 45°

Question 3.
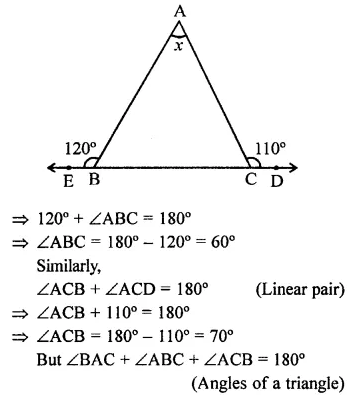
Compute the value of x in each of the following figures:
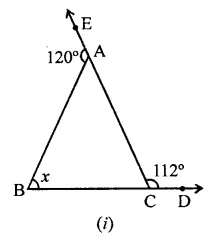
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q3.1

RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q3.2

Solution:
(i) In ∆ABC, sides BC and CA are produced to D and E respectively

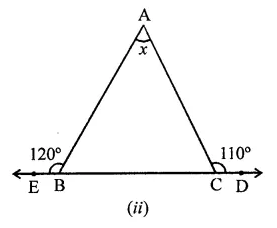
(ii) In ∆ABC, side BC is produced to either side to D and E respectively
∠ABE = 120° and ∠ACD =110°
∵ ∠ABE + ∠ABC = 180° (Linear pair)
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q3.6

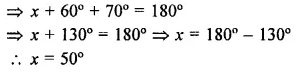
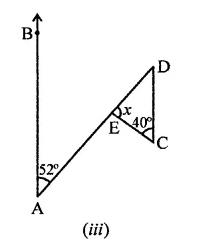
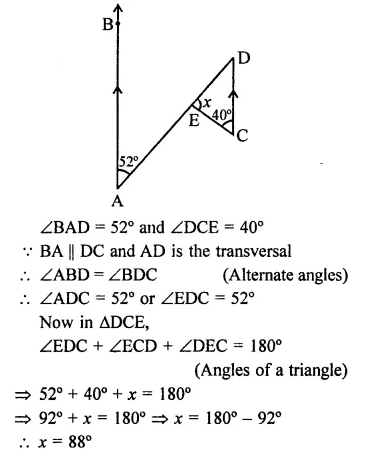
(iii) In the figure, BA || DC
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q3.8

Question 4.
In the figure, AC ⊥ CE and ∠A: ∠B : ∠C = 3:2:1, find the value of ∠ECD.
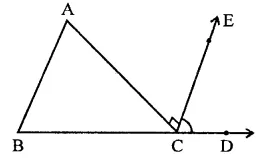
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q4.1
Solution:
In ∆ABC, ∠A : ∠B : ∠C = 3 : 2 : 1
BC is produced to D and CE ⊥ AC
∵ ∠A + ∠B + ∠C = 180° (Sum of angles of a triangles)
Let∠A = 3x, then ∠B = 2x and ∠C = x
∴ 3x + 2x + x = 180° ⇒ 6x = 180°
⇒ x = \(\frac { { 180 }^{ \circ } }{ 6 }\) = 30°
∴ ∠A = 3x = 3 x 30° = 90°
∠B = 2x = 2 x 30° = 60°
∠C = x = 30°
In ∆ABC,
Ext. ∠ACD = ∠A + ∠B
⇒ 90° + ∠ECD = 90° + 60° = 150°
∴ ∠ECD = 150°-90° = 60°

Question 5.
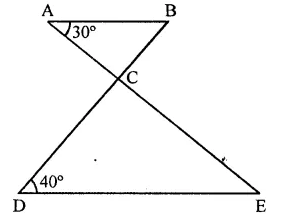
In the figure, AB || DE, find ∠ACD.
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q5.1
Solution:
In the figure, AB || DE
AE and BD intersect each other at C ∠BAC = 30° and ∠CDE = 40°
∵ AB || DE
∴ ∠ABC = ∠CDE (Alternate angles)

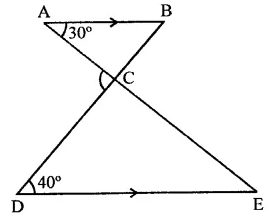
⇒ ∠ABC = 40°
In ∆ABC, BC is produced
Ext. ∠ACD = Int. ∠A + ∠B
= 30° + 40° = 70°

Question 6.
Which of the following statements are true (T) and which are false (F):
(i) Sum of the three angles of a triangle is 180°.
(ii) A triangle can have two right angles.
(iii) All the angles of a triangle can be less than 60°.
(iv) All the angles of a triangle can be greater than 60°.
(v) All the angles of a triangle can be equal to 60°.
(vi) A triangle can have two obtuse angles.
(vii) A triangle can have at most one obtuse angles.
(viii) If one angle of a triangle is obtuse, then it cannot be a right angled triangle.
(ix) An exterior angle of a triangle is less than either of its interior opposite angles.
(x) An exterior angle of a triangle is equal to the sum of the two interior opposite angles.
(xi) An exterior angle of a triangle is greater than the opposite interior angles.
Solution:
(i) True.
(ii) False. A right triangle has only one right angle.
(iii) False. In this, the sum of three angles will be less than 180° which is not true.
(iv) False. In this, the sum of three angles will be more than 180° which is not true.
(v) True. As sum of three angles will be 180° which is true.
(vi) False. A triangle has only one obtuse angle.
(vii) True.
(viii)True.
(ix) False. Exterior angle of a triangle is always greater than its each interior opposite angles.
(x) True.
(xi) True.

Question 7.
Fill in the blanks to make the following statements true:
(i) Sum of the angles of a triangle is ………
(ii) An exterior angle of a triangle is equal to the two …….. opposite angles.
(iii) An exterior angle of a triangle is always …….. than either of the interior opposite angles.
(iv) A triangle cannot have more than ………. right angles.
(v) A triangles cannot have more than ……… obtuse angles.
Solution:
(i) Sum of the angles of a triangle is 180°.
(ii) An exterior angle of a triangle is equal to the two interior opposite angles.
(iii) An exterior angle of a triangle is always greater than either of the interior opposite angles.
(iv) A triangle cannot have more than one right angles.
(v) A triangles cannot have more than one obtuse angles.

Question 8.
In a ∆ABC, the internal bisectors of ∠B and ∠C meet at P and the external bisectors of ∠B and ∠C meet at Q. Prove that ∠BPC + ∠BQC = 180°.
Solution:
Given : In ∆ABC, sides AB and AC are produced to D and E respectively. Bisectors of interior ∠B and ∠C meet at P and bisectors of exterior angles B and C meet at Q.
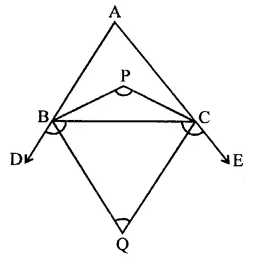
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q8.1
To prove : ∠BPC + ∠BQC = 180°
Proof : ∵ PB and PC are the internal bisectors of ∠B and ∠C
∠BPC = 90°+ \(\frac { 1 }{ 2 }\) ∠A …(i)
Similarly, QB and QC are the bisectors of exterior angles B and C
∴ ∠BQC = 90° + \(\frac { 1 }{ 2 }\) ∠A …(ii)
Adding (i) and (ii),
∠BPC + ∠BQC = 90° + \(\frac { 1 }{ 2 }\) ∠A + 90° – \(\frac { 1 }{ 2 }\) ∠A
= 90° + 90° = 180°
Hence ∠BPC + ∠BQC = 180°

Question 9.
In the figure, compute the value of x.
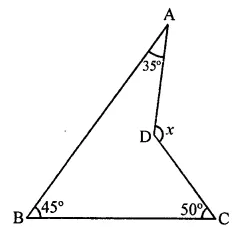
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q9.1
Solution:
In the figure,
∠ABC = 45°, ∠BAD = 35° and ∠BCD = 50° Join BD and produce it E

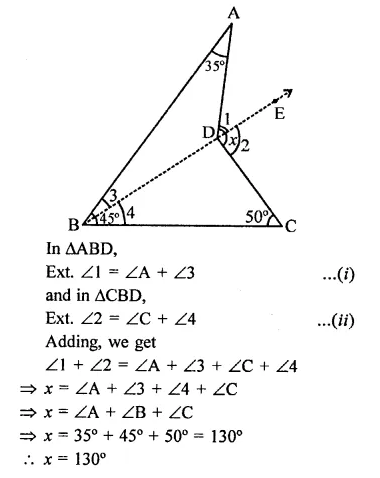
Question 10.
In the figure, AB divides ∠D AC in the ratio 1 : 3 and AB = DB. Determine the value of x.
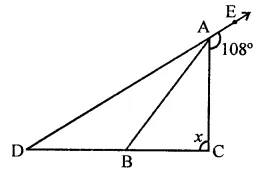
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q10.1
Solution:
In the figure AB = DB

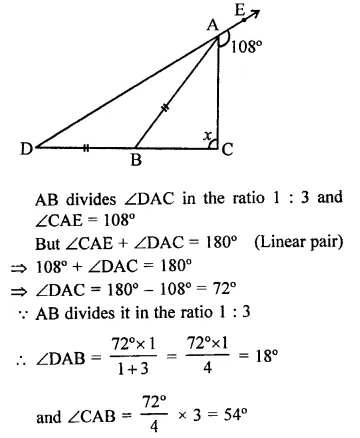
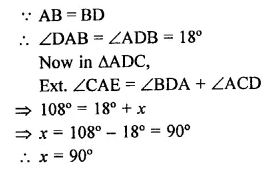
Question 11.
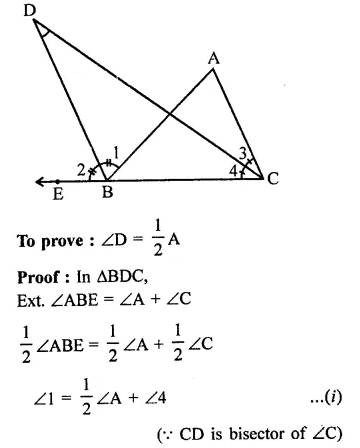
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \(\frac { 1 }{ 2 }\) ∠A.
Solution:
Given : In ∠ABC, CB is produced to E bisectors of ext. ∠ABE and into ∠ACB meet at D.
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q11.1

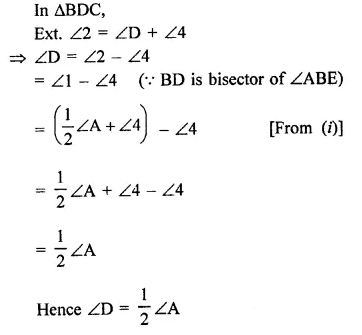
Question 12.
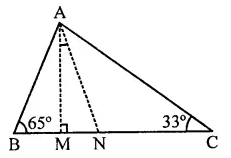
In the figure, AM ⊥ BC and AN is the bisector of ∠A. If ∠B = 65° and ∠C = 33°, find ∠MAN.
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q12.1
Solution:

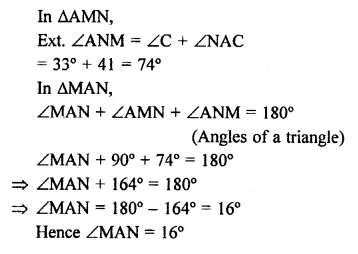
Question 13.
In a AABC, AD bisects ∠A and ∠C > ∠B. Prove that ∠ADB > ∠ADC.
Solution:
Given : In ∆ABC,
∠C > ∠B and AD is the bisector of ∠A
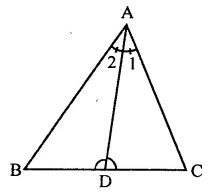
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q13.1
To prove : ∠ADB > ∠ADC
Proof: In ∆ABC, AD is the bisector of ∠A
∴ ∠1 = ∠2
In ∆ADC,
Ext. ∠ADB = ∠l+ ∠C
⇒ ∠C = ∠ADB – ∠1 …(i)
Similarly, in ∆ABD,
Ext. ∠ADC = ∠2 + ∠B
⇒ ∠B = ∠ADC – ∠2 …(ii)
From (i) and (ii)
∵ ∠C > ∠B (Given)
∴ (∠ADB – ∠1) > (∠ADC – ∠2)
But ∠1 = ∠2
∴ ∠ADB > ∠ADC

Question 14.
In ∆ABC, BD ⊥ AC and CE ⊥ AB. If BD and CE intersect at O, prove that ∠BOC = 180°-∠A.
Solution:
Given : In ∆ABC, BD ⊥ AC and CE⊥ AB BD and CE intersect each other at O
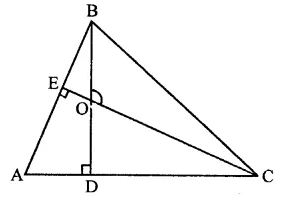
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q14.1
To prove : ∠BOC = 180° – ∠A
Proof: In quadrilateral ADOE
∠A + ∠D + ∠DOE + ∠E = 360° (Sum of angles of quadrilateral)
⇒ ∠A + 90° + ∠DOE + 90° = 360°
∠A + ∠DOE = 360° – 90° – 90° = 180°
But ∠BOC = ∠DOE (Vertically opposite angles)
⇒ ∠A + ∠BOC = 180°
∴ ∠BOC = 180° – ∠A

Question 15.
In the figure, AE bisects ∠CAD and ∠B = ∠C. Prove that AE || BC.
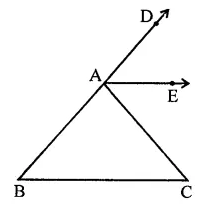
RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 Q15.1
Solution:
Given : In AABC, BA is produced and AE is the bisector of ∠CAD
∠B = ∠C

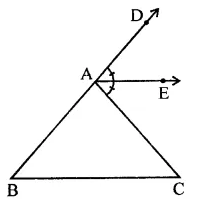
To prove : AE || BC
Proof: In ∆ABC, BA is produced
∴ Ext. ∠CAD = ∠B + ∠C
⇒ 2∠EAC = ∠C + ∠C (∵ AE is the bisector of ∠CAE) (∵ ∠B = ∠C)
⇒ 2∠EAC = 2∠C
⇒ ∠EAC = ∠C
But there are alternate angles
∴ AE || BC

Hope given RD Sharma Class 9 Solutions Chapter 11 Co-ordinate Geometry Ex 11.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.