RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2

Other Exercises

• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Question 1.
The radius of a circle is 8 cm and the length of one of its chords is 12 cm. Find the distance of the chord from the centre.
Solution:
Radius of circle with centre O is OA = 8 cm
Length of chord AB = 12 cm
OC ⊥ AB which bisects AB at C

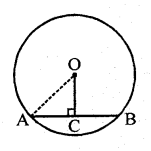
∴ AC = CB = 12 x \(\frac { 1 }{ 2 }\) = 6 cm
In ∆OAC,
OA2 = OC2 + AC2 (Pythagoras Theorem)
⇒ (8)2 = OC2 + (6)2
⇒ 64 = OC2 + 36
OC2 = 64 – 36 = 28
∴ OC = \(\sqrt { 28 } \) = \(\sqrt { 4×7 } \) cm
= 2 x 2.6457 = 5.291 cm

Question 2.
Find the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 10 cm.
Solution:
Let AB be a chord of a circle with radius 10 cm. OC ⊥ AB
∴ OA = 10 cm
OC = 5 cm

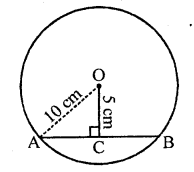
∵ OC divides AB into two equal parts
i.e. AC = CB
Now in right AOAC,
OA2 = OC2 + AC2 (Pythagoras Theorem)
⇒ (10)2 = (5)2 + AC2
⇒ 100 = 25 + AC2
⇒ AC2 = 100 – 25 = 75
∴ AC = \(\sqrt { 75 } \)= \(\sqrt { 25×3 } \) = 5 x 1.732
∴ AB = 2 x AC = 2 x 5 x 1.732 = 10 x 1.732 = 17.32 cm

Question 3.
Find the length of a chord which is at a distance of 4 cm from the centre of the circle of radius 6 cm.
Solution:
In a circle with centre O and radius 6 cm and a chord AB at a distance of 4 cm from the centre of the circle
i.e. OA = 6 cm and OL ⊥ AB, OL = 4 cm

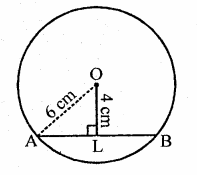
∵ Perpendicular OL bisects the chord AB at L 1
∴ AL = LB=\(\frac { 1 }{ 2 }\) AB
Now in right ∆OAL,
OA2 = OL2 + AL2 (Pythagoras Theorem)
(6)2 = (4)2 + AL2
⇒ 36=16+AL2
⇒ AL2 = 36 – 16 = 20
∴ AL = \(\sqrt { 20 } \) = \(\sqrt { 4×5 } \) = 2 x 2.236 = 4.472 cm
∴ Chord AB = 4.472 x 2 = 8.944 = 8.94 cm

Question 4.
Give a method to find the centre of a given circle.
Solution:
Steps of construction :

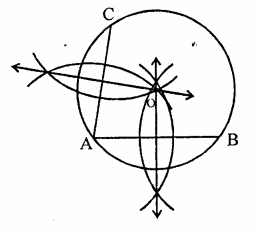
(i) Take three distinct points on the circle say A, B and C.
(ii) Join AB and AC.
(iii) Draw the perpendicular bisectors of AB and AC which intersect each other at O.
O is the required centre of the given circle

Question 5.
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
Solution:
Given : In circle with centre O
CD is the diameter and AB is the chord
which is bisected by diameter at E
OA and OB are joined

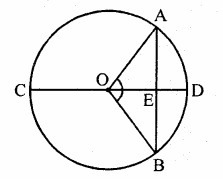
To prove : ∠AOB = ∠BOA
Proof : In ∆OAE and ∆OBE
OA = OB (Radii of the circle)
OE = OE (Common)
AE = EB (Given)
∴ ∆OAE = ∆OBE (SSS criterian)
∴ ∠AOE = ∠BOE (c.p.c.t.)
Hence diameter bisect the angle subtended by the chord AB.

Question 6.
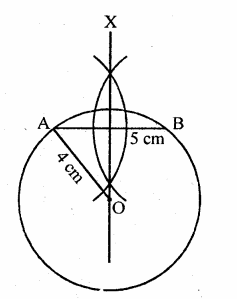
A line segment AB is of length 5 cm. Draw a circle of radius 4 cm passing through A and B. Can you draw a circle of radius 2 cm passing through A and B? Give reason in support of your answer.
Solution:
Steps of construction :
(i) Draw a line segment AB = 5 cm.
(ii) Draw a perpendicular bisector of AB.
(iii) With centre A and radius 4 cm, draw an arc which intersects the perpendicular bisector at O.
(iv) With centre O and radius 4 cm, draw a circle which passes through A and B.
With radius 2 cm, we cannot draw the circle passing through A and B as diameter
i. e. 2 + 2 = 4 cm is shorder than 5 cm.

Question 7.
An equilateral triangle of side 9 cm is inscribed in a circle. Find the radius of the circle.
Solution:
Steps of construction :
(i) Draw a line segment BC = 9 cm.
(ii) With centres B and C, draw arcs of 9 cm radius which intersect each other at A.
(iii) Join AB and AC.
∆ABC is the required triangle.
(iv) Draw perpendicular bisectors of sides AB and BC which intersect each other at O.
(v) With centre O and radius OB, draw a circle which passes through A, B and C.
This is the require circle in which ∆ABC is inscribed.

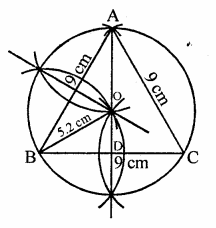
On measuring its radius, it is 5.2 cm

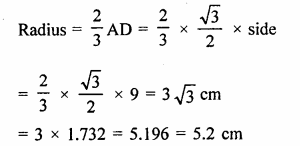
Question 8.
Given an arc of a circle, complete the circle.
Solution:
Steps of construction :
(i) Take three points A, B and C on the arc and join AB and BC.
(ii) Draw the perpendicular bisector of AB and BC which intersect each other at O.

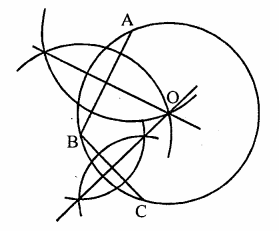
(iii) With centre O and radius OA or OB, complete the circle.
This is the required circle.

Question 9.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Solution:
Below, three different pairs of circles are drawn:


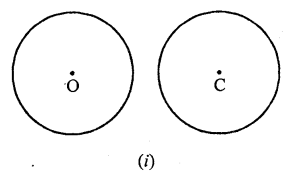
(i) In the first pair, two circles do not intersect each other. Therefore they have no point in common. .
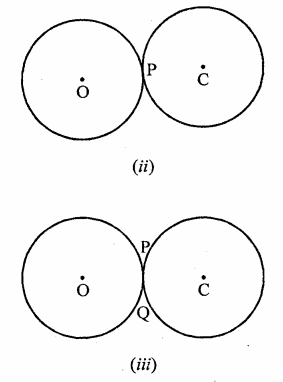
(ii) In the second pair, two circles intersect (touch) each other at one point P. Therefore they have one point in common.
(iii) In the third pair, two circles intersect each other at two points. Therefore they have two points in common.
There is no other possibility of two circles intersecting each other.
Therefore, two circles have at the most two points in common.

Question 10.
Suppose you are given a circle. Give a construction to find its centre.
Solution:
See Q. No. 4 of this exercise.

Question 11.
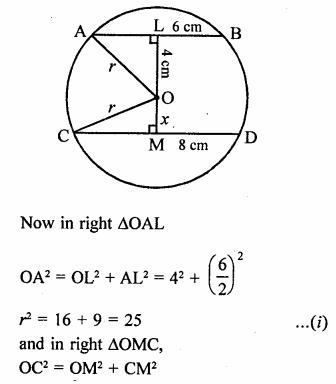
The length of two parallel chords of a circle are 6 cm and 8 cm. If the smaller chord is at a distance of 4 cm from the centre, what is the distance of the other chord from the centre? [NCERT]
Solution:
A circle with centre O and two parallel chords
AB and CD are AB = 6 cm, CD = 8 cm
Let OL ⊥ AB and OM ⊥ CD
∴ OL = 4 cm
Let OM = x cm
Let r be the radius of the circle

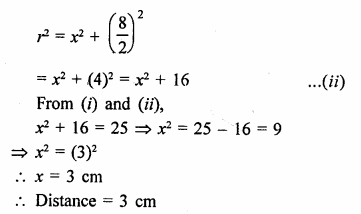
Question 12.
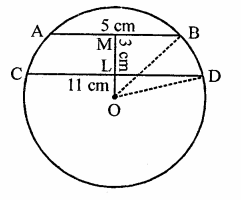
Two chords AB, CD of lengths 5 cm and 11 cm respectively of a circle are parallel. If the distance between AB and CD is 3 cm, find the radius of the circle.
Solution:
Let two chords AB and CD of length 5 cm and 11 cm are parallel to each other AB = 5 cm, CD = 11 cm
Distance between AB and LM = 3 cm
Join OB and OD
OL and OM are the perpendicular on CD and AB respectively. Which bisects AB and CD.
Let OL = x, then OM = (x + 3)

Now in right ∆OLD,
OD² = OL² + LD²
= x² + (5.5)²
Similarly in right ∆OMB,
OB² = OM² + MB² = (x + 3)² + (2.5)²
But OD = OB (Radii of the circle)
∴ (x + 3)² + (2.5)² = x² + (5.5)²
x² + 6x + 9 + 6.25 = x² + 30.25
6x = 30.25 – 6.25 – 9 = 15

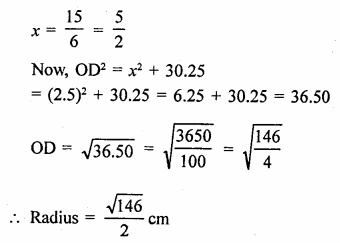
Question 13.
Prove that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
Solution:
Given : A circle with centre O and a chord AB
Let M be the mid point of AB and OM is joined and produced to meet the minor arc AB at N
To prove : M is the mid point of arc AB
Construction : Join OA, OB

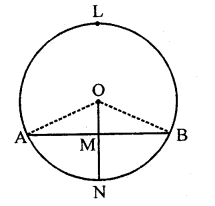
Proof: ∵ M is mid point of AB
∴ OM ⊥ AB
In AOAM and OBM,
OA = OB (Radii of the circle)
OM = OM (common)
AM = BM (M is mid point of AB)
∴ ∆OAM = ∆OBM (SSS criterian)
∴ ∠AOM = ∠BOM (c.p.c.t.)
⇒ ∠AOM = ∠BOM
But these are centre angles at the centre made by arcs AN and BN
∴ Arc AN = Arc BN
Hence N divides the arc in two equal parts

Question 14.
Prove that two different circles cannot intersect each other at more than two points.
Solution:
Given : Two circles
To prove : They cannot intersect each other more than two points
Construction : Let two circles intersect each other at three points A, B and C

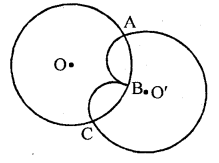
Proof : Since two circles with centres O and O’ intersect at A, B and C
∴ A, B and C are non-collinear points
∴ Circle with centre O passes through three points A, B and C
and circle with centre O’ also passes through three points A, B and C
But one and only one circle can be drawn through three points
∴Our supposition is wrong
∴ Two circle cannot intersect each other not more than two points.

Question 15.
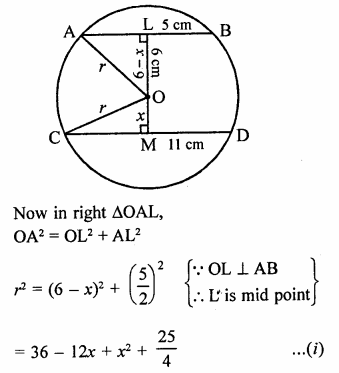
Two chords AB and CD of lengths 5 cm and 11 cm respectively of a circle are parallel to each other and are opposite side of its centre. If the distance between AB and CD is 6 cm, find the radius of the circle. [NCERT]
Solution:
Let r be the radius of the circle with centre O.
Two parallel chords AB = 5 cm, CD = 11 cm
Let OL ⊥ AB and OM ⊥CD
∴ LM = 6 cm
Let OM = x, then
OL = 6 – x

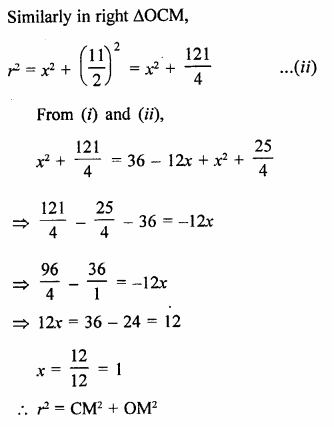
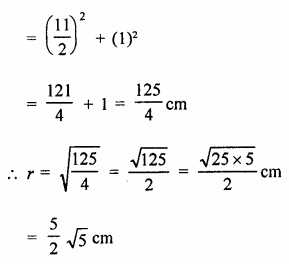
Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.