RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4

Other Exercises

• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Question 1.
In the figure, O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

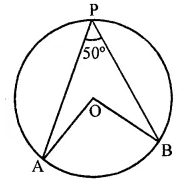
Solution:
Arc AB, subtends ∠AOB at the centre and ∠APB at the remaining part of the circle
∴∠AOB = 2∠APB = 2 x 50° = 100°
Join AB

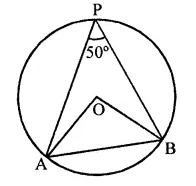
∆AOB is an isosceles triangle in which
OA = OB
∴ ∠OAB = ∠OBA But ∠AOB = 100°
∴∠OAB + ∠OBA = 180° – 100° = 80°
⇒ 2∠OAB = 80°
80°
∴∠OAB = \(\frac { { 80 }^{ \circ } }{ 2 }\)  = 40°

Question 2.
In the figure, O is the centre of the circle. Find ∠BAC.

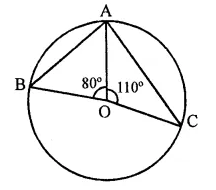
Solution:
In the circle with centre O
∠AOB = 80° and ∠AOC =110°
∴ ∠BOC = ∠AOB + ∠AOC
= 80°+ 110°= 190°
∴ Reflex ∠BOC = 360° – 190° = 170°
Now arc BEC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle.

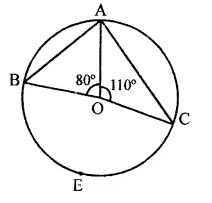
∴ ∠BOC = 2∠BAC
⇒ 170° = 2∠BAC
⇒ ∠BAC = \(\frac { { 170 }^{ \circ } }{ 2 }\) = 85°
∴ ∠BAC = 85°

Question 3.
If O is the centre of the circle, find the value of x in each of the following figures:



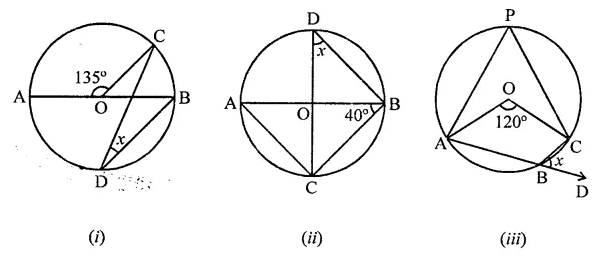
Solution:
(i) A circle with centre O
∠AOC = 135°
But ∠AOC + ∠COB = 180° (Linear pair)
⇒ 135° + ∠COB = 180°
⇒ ∠COB = 180°- 135° = 45°
Now arc BC subtends ∠BOC at the centre and ∠BPC at the remaining part of the circle
∴ ∠BOC = 2∠BPC
⇒ ∠BPC = \(\frac { 1 }{ 2 }\)∠BOC = \(\frac { 1 }{ 2 }\) x 45° = \(\frac { { 45 }^{ \circ } }{ 2 }\)
∴ ∠BPC = 22 \(\frac { 1 }{ 2 }\)° or x = 22 \(\frac { 1 }{ 2 }\)°
(ii) ∵ CD and AB are the diameters of the circle with centre O
∠ABC = 40°
But in ∆OBC,
OB = OC (Radii of the circle)
∠OCB = ∠OBC – 40°
Now in ABCD,
∠ODB + ∠OCB + ∠CBD = 180° (Angles of a triangle)
⇒ x + 40° + 90° = 180°
⇒ x + 130° = 180°
⇒ x = 180° – 130° = 50°
∴ x = 50°
(iii) In circle with centre O,
∠AOC = 120°, AB is produced to D
∵ ∠AOC = 120°
and ∠AOC + convex ∠AOC = 360°
⇒ 120° + convex ∠AOC = 360°
∴ Convex ∠AOC = 360° – 120° = 240°
∴ Arc APC Subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle
∴ ∠ABC = \(\frac { 1 }{ 2 }\)∠AOC = \(\frac { 1 }{ 2 }\)x 240° = 120°
But ∠ABC + ∠CBD = 180° (Linear pair)
⇒ 120° + x = 180°
⇒ x = 180° – 120° = 60°
∴ x = 60°
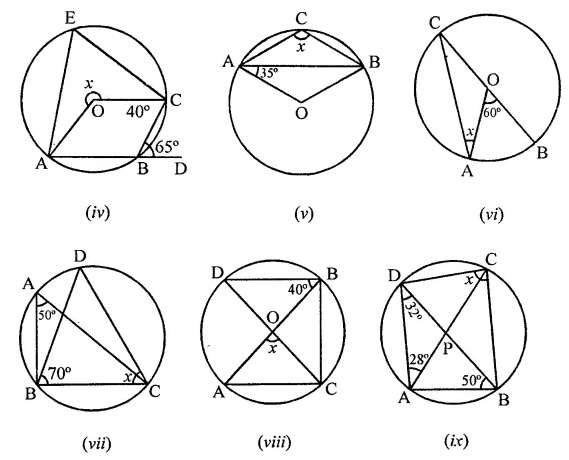
(iv) A circle with centre O and ∠CBD = 65°
But ∠ABC + ∠CBD = 180° (Linear pair)
⇒ ∠ABC + 65° = 180°
⇒ ∠ABC = 180°-65°= 115°
Now arc AEC subtends ∠x at the centre and ∠ABC at the remaining part of the circle
∴ ∠AOC = 2∠ABC
⇒ x = 2 x 115° = 230°
∴ x = 230°
(v) In circle with centre O
AB is chord of the circle, ∠OAB = 35°
In ∆OAB,
OA = OB (Radii of the circle)
∠OBA = ∠OAB = 35°
But in ∆OAB,
∠OAB + ∠OBA + ∠AOB = 180° (Angles of a triangle)
⇒ 35° + 35° + ∠AOB = 180°
⇒ 70° + ∠AOB = 180°
⇒ ∠AOB = 180°-70°= 110°
∴ Convex ∠AOB = 360° -110° = 250°
But arc AB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle.
∴∠ACB = \(\frac { 1 }{ 2 }\)∠AOB
⇒ x = \(\frac { 1 }{ 2 }\) x 250° = 125°
∴ x= 125°
(vi) In the circle with centre O,
BOC is its diameter, ∠AOB = 60°
Arc AB subtends ∠AOB at the centre of the circle and ∠ACB at the remaining part of the circle
∴ ∠ACB = \(\frac { 1 }{ 2 }\) ∠AOB
= \(\frac { 1 }{ 2 }\) x 60° = 30°
But in ∆OAC,
OC = OA (Radii of the circle)
∴ ∠OAC = ∠OCA = ∠ACB
⇒ x = 30°
(vii) In the circle, ∠BAC and ∠BDC are in the same segment
∴ ∠BDC = ∠BAC = 50°
Now in ABCD,
∠DBC + ∠BCD + ∠BDC = 180° (Angles of a triangle)
⇒ 70° + x + 50° = 180°
⇒ x + 120° = 180° ⇒ x = 180° – 120° = 60°
∴ x = 60°
(viii) In circle with centre O,
∠OBD = 40°
AB and CD are diameters of the circle
∠DBA and ∠ACD are in the same segment
∴ ∠ACD = ∠DBA = 40°
In AOAC, OA = OC (Radii of the circle)
∴ ∠OAC = ∠OCA = 40°
and ∠OAC + ∠OCA + ∠AOC = 180° (Angles in a triangle)
⇒ 40° + 40° + x = 180°
⇒ x + 80° = 180° ⇒ x = 180° – 80° = 100°
∴ x = 100°
(ix) In the circle, ABCD is a cyclic quadrilateral ∠ADB = 32°, ∠DAC = 28° and ∠ABD = 50°
∠ABD and ∠ACD are in the same segment of a circle
∴ ∠ABD = ∠ACD ⇒ ∠ACD = 50°
Similarly, ∠ADB = ∠ACB
⇒ ∠ACB = 32°
Now, ∠DCB = ∠ACD + ∠ACB
= 50° + 32° = 82°
∴ x = 82°
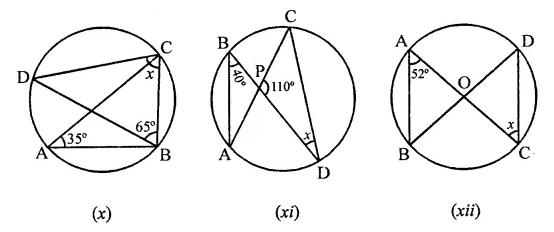
(x) In a circle,
∠BAC = 35°, ∠CBD = 65°
∠BAC and ∠BDC are in the same segment
∴ ∠BAC = ∠BDC = 35°
In ∆BCD,
∠BDC + ∠BCD + ∠CBD = 180° (Angles in a triangle)
⇒ 35° + x + 65° = 180°
⇒ x + 100° = 180°
⇒ x = 180° – 100° = 80°
∴ x = 80°
(xi) In the circle,
∠ABD and ∠ACD are in the same segment of a circle
∴ ∠ABD = ∠ACD = 40°
Now in ∆CPD,
∠CPD + ∠PCD + ∠PDC = 180° (Angles of a triangle)
110° + 40° + x = 180°
⇒ x + 150° = 180°
∴ x= 180°- 150° = 30°
(xii) In the circle, two diameters AC and BD intersect each other at O
∠BAC = 50°
In ∆OAB,
OA = OB (Radii of the circle)
∴ ∠OBA = ∠OAB = 52°
⇒ ∠ABD = 52°
But ∠ABD and ∠ACD are in the same segment of the circle
∴ ∠ABD = ∠ACD ⇒ 52° = x
∴ x = 52°

Question 4.
O is the circumcentre of the triangle ABC and OD is perpendicular on BC. Prove that ∠BOD = ∠A.
Solution:
Given : O is the circumcentre of ∆ABC.
OD ⊥ BC
OB is joined
To prove : ∠BOD = ∠A
Construction : Join OC.

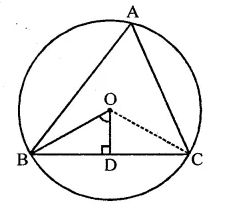
Proof : Arc BC subtends ∠BOC at the centre and ∠BAC at the remaining part of the circle
∴ ∠BOC = 2∠A …(i)
In right ∆OBD and ∆OCD Side OD = OD (Common)
Hyp. OB = OC (Radii of the circle)
∴ ∆OBD ≅ ∆OCD (RHS criterion)
∴ ∠BOD = ∠COD = \(\frac { 1 }{ 2 }\) ∠BOC
⇒ ∠BOC = 2∠BOD …(ii)
From (i) and (ii)
2∠BOD = 2∠A
∴∠BOD = ∠A

Question 5.
In the figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = BC.

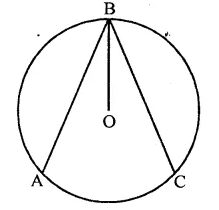
Solution:
Given : In the figure, a circle with centre O OB is the bisector of ∠ABC
To prove : AB = BC
Construction : Draw OL ⊥ AB and OM ⊥ BC

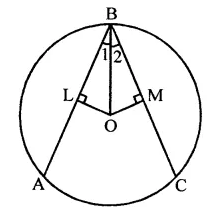
Proof: In ∆OLB and ∆OMB,
∠1 = ∠2 (Given)
∠L = ∠M (Each = 90°)
OB = OB (Common)
∴ ∆OLB ≅ ∆OMB (AAS criterion)
∴ OL = OM (c.p.c.t.)
But these are distance from the centre and chords equidistant from the centre are equal
∴ Chord BA = BC
Hence AB = BC

Question 6.
In the figure, O and O’ are centres of two circles intersecting at B and C. ACD is a straight line, find x.

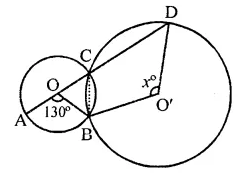
Solution:
In the figure, two circles with centres O and O’ intersect each other at B and C.
ACD is a line, ∠AOB = 130°
Arc AB subtends ∠AOB at the centre O and ∠ACB at the remaining part of the circle.

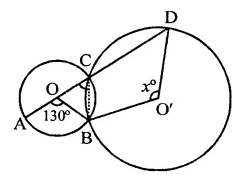
∴ ∠ACB =\(\frac { 1 }{ 2 }\)∠AOB
= \(\frac { 1 }{ 2 }\) x 130° = 65°
But ∠ACB + ∠BCD = 180° (Linear pair)
⇒ 65° + ∠BCD = 180°
⇒ ∠BCD = 180°-65°= 115°
Now, arc BD subtends reflex ∠BO’D at the centre and ∠BCD at the remaining part of the circle
∴ ∠BO’D = 2∠BCD = 2 x 115° = 230°
But ∠BO’D + reflex ∠BO’D = 360° (Angles at a point)
⇒ x + 230° = 360°
⇒ x = 360° -230°= 130°
Hence x = 130°

Question 7.
In the figure, if ∠ACB = 40°, ∠DPB = 120°, find ∠CBD.

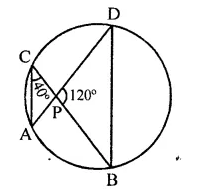
Solution:
Arc AB subtend ∠ACB and ∠ADB in the same segment of a circle
∴ ∠ACB = ∠ADB = 40°
In ∆PDB,
∠DPB + ∠PBD + ∠ADB = 180° (Sum of angles of a triangle)
⇒ 120° + ∠PBD + 40° = 180°
⇒ 160° + ∠PBD = 180°
⇒ ∠PBD = 180° – 160° = 20°
⇒ ∠CBD = 20°

Question 8.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
Solution:
A circle with centre O, a chord AB = radius of the circle C and D are points on the minor and major arcs of the circle

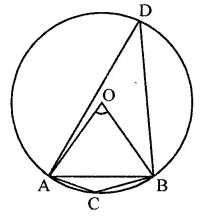
∴ ∠ACB and ∠ADB are formed Now in ∆AOB,
OA = OB = AB (∵ AB = radii of the circle)
∴ ∆AOB is an equilateral triangle,
∴ ∠AOB = 60°
Now arc AB subtends ∠AOB at the centre and ∠ADB at the remainder part of the circle.
∴ ∠ADB = \(\frac { 1 }{ 2 }\) ∠AOB = \(\frac { 1 }{ 2 }\)x 60° = 30°
Now ACBD is a cyclic quadrilateral,
∴ ∠ADB + ∠ACB = 180° (Sum of opposite angles of cyclic quad.)
⇒ 30° + ∠ACB = 180°
⇒ ∠ACB = 180° – 30° = 150°
∴ ∠ACB = 150°
Hence angles are 150° and 30°

Question 9.
In the figure, it is given that O is the centre of the circle and ∠AOC = 150°. Find ∠ABC.

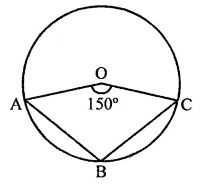
Solution:
In circle with centre O and ∠AOC = 150°
But ∠AOC + reflex ∠AOC = 360°
∴ 150° + reflex ∠AOC = 360°
⇒ Reflex ∠AOC = 360° – 150° = 210°
Now arc AEC subtends ∠AOC at the centre and ∠ABC at the remaining part of the circle.

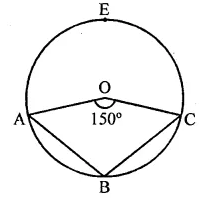
Reflex ∠AOC = 2∠ABC
⇒ 210° = 2∠ABC
∴ ∠ABC = \(\frac { { 210 }^{ \circ } }{ 2 }\)  = 105°

Question 10.
In the figure, O is the centre of the circle, prove that ∠x = ∠y + ∠z.
Solution:
Given : In circle, O is centre

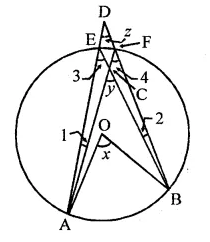
To prove : ∠x = ∠y + ∠z
Proof : ∵ ∠3 and ∠4 are in the same segment of the circle
∴ ∠3 = ∠4 …(i)
∵ Arc AB subtends ∠AOB at the centre and ∠3 at the remaining part of the circle
∴ ∠x = 2∠3 = ∠3 + ∠3 = ∠3 + ∠4 (∵ ∠3 = ∠4) …(ii)
In ∆ACE,
Ext. ∠y = ∠3 + ∠1
(Ext. is equal to sum of its interior opposite angles)
⇒ ∠3 – ∠y – ∠1 …(ii)
From (i) and (ii),
∠x = ∠y – ∠1 + ∠4 …(iii)
Similarly in ∆ADF,
Ext. ∠4 = ∠1 + ∠z …(iv)
From (iii) and (iv)
∠x = ∠y-∠l + (∠1 + ∠z)
= ∠y – ∠1 + ∠1 + ∠z = ∠y + ∠z
Hence ∠x = ∠y + ∠z

Question 11.
In the figure, O is the centre of a circle and PQ is a diameter. If ∠ROS = 40°, find ∠RTS.

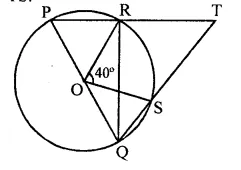
Solution:
In the figure, O is the centre of the circle,
PQ is the diameter and ∠ROS = 40°
Now we have to find ∠RTS
Arc RS subtends ∠ROS at the centre and ∠RQS at the remaining part of the circle

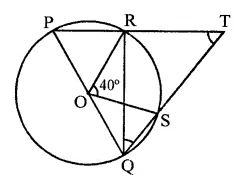
∴ ∠RQS = \(\frac { 1 }{ 2 }\) ∠ROS
= \(\frac { 1 }{ 2 }\) x 40° = 20°
∵ ∠PRQ = 90° (Angle in a semi circle)
∴ ∠QRT = 180° – 90° = 90° (∵ PRT is a straight line)
Now in ∆RQT,
∠RQT + ∠QRT + ∠RTQ = 180° (Angles of a triangle)
⇒ 20° + 90° + ∠RTQ = 180°
⇒ ∠RTQ = 180° – 20° – 90° = 70° or ∠RTS = 70°
Hence ∠RTS = 70°

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.