RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5

RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5

Other Exercises

• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
• RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS

Question 1.
In the figure, ∆ABC is an equilateral triangle. Find m ∠BEC.

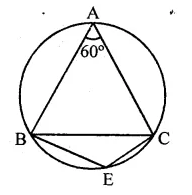
Solution:
∵ ∆ABC is an equilateral triangle
∴ A = 60°
∵ ABEC is a cyclic quadrilateral
∴ ∠A + ∠E = 180° (Sum of opposite angles)
⇒ 60° + ∠E = 180°
⇒ ∠E = 180° – 60° = 120°
∴ m ∠BEC = 120°

Question 2.
In the figure, ∆PQR is an isosceles triangle with PQ = PR and m ∠PQR = 35°. Find m ∠QSR and m ∠QTR.

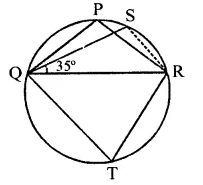
Solution:
In the figure, ∆PQR is an isosceles PQ = PR
∠PQR = 35°
∴ ∠PRQ = 35°
But ∠PQR + ∠PRQ + ∠QPR = 180° (Sum of angles of a triangle)
⇒ 35° + 35° + ∠QPR = 180°
⇒ 70° + ∠QPR = 180°
∴ ∠QPR = 180° – 70° = 110°
∵ ∠QSR = ∠QPR (Angle in the same segment of circles)
∴ ∠QSR = 110°
But PQTR is a cyclic quadrilateral
∴ ∠QTR + ∠QPR = 180°
⇒ ∠QTR + 110° = 180°
⇒ ∠QTR = 180° -110° = 70°
Hence ∠QTR = 70°

Question 3.
In the figure, O is the centre of the circle. If ∠BOD = 160°, find the values of x and y.

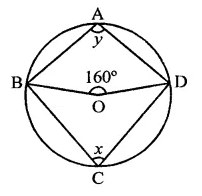
Solution:
In the figure, O is the centre of the circle ∠BOD =160°
ABCD is the cyclic quadrilateral
∵ Arc BAD subtends ∠BOD is the angle at the centre and ∠BCD is on the other part of the circle
∴ ∠BCD = \(\frac { 1 }{ 2 }\) ∠BOD
⇒ x = \(\frac { 1 }{ 2 }\) x 160° = 80°
∵ ABCD is a cyclic quadrilateral,
∴ ∠A + ∠C = 180°
⇒ y + x = 180°
⇒ y + 80° = 180°
⇒ y =180°- 80° = 100°
∴ x = 80°, y = 100°

Question 4.
In the figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

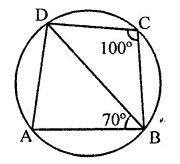
Solution:
In a circle, ABCD is a cyclic quadrilateral ∠BCD = 100° and ∠ABD = 70°
∵ ABCD is a cyclic quadrilateral,
∴ ∠A + ∠C = 180° (Sum of opposite angles)

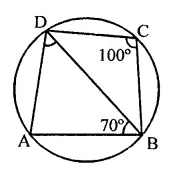
⇒ ∠A + 100°= 180°
∠A = 180°- 100° = 80°
Now in ∆ABD,
∠A + ∠ABD + ∠ADB = 180°
⇒ 80° + 70° + ∠ADB = 180°
⇒ 150° +∠ADB = 180°
∴ ∠ADB = 180°- 150° = 30°
Hence ∠ADB = 30°

Question 5.
If ABCD is a cyclic quadrilateral in which AD || BC. Prove that ∠B = ∠C.

Solution:
Given : ABCD is a cyclic quadrilateral in which AD || BC

To prove : ∠B = ∠C
Proof : ∵ AD || BC
∴ ∠A + ∠B = 180°
(Sum of cointerior angles)
But ∠A + ∠C = 180°
(Opposite angles of the cyclic quadrilateral)
∴ ∠A + ∠B = ∠A + ∠C
⇒ ∠B = ∠C
Hence ∠B = ∠C

Question 6.
In the figure, O is the centre of the circle. Find ∠CBD.

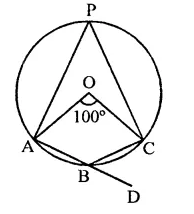
Solution:
Arc AC subtends ∠AOC at the centre and ∠APC at the remaining part of the circle

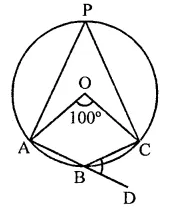
∴ ∠APC = \(\frac { 1 }{ 2 }\) ∠AOC
= \(\frac { 1 }{ 2 }\) x 100° = 50°
∵ APCB is a.cyclic quadrilateral,
∴ ∠APC + ∠ABC = 180°
⇒ 50° + ∠ABC = 180° ⇒ ∠ABC =180°- 50°
∴ ∠ABC =130°
But ∠ABC + ∠CBD = 180° (Linear pair)
⇒ 130° + ∠CBD = 180°
⇒ ∠CBD = 180°- 130° = 50°
∴ ∠CBD = 50°

Question 7.
In the figure, AB and CD are diameiers of a circle with centre O. If ∠OBD = 50°, find ∠AOC.

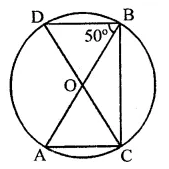
Solution:
Two diameters AB and CD intersect each other at O. AC, CB and BD are joined

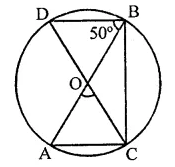
∠DBA = 50°
∠DBA and ∠DCA are in the same segment
∴ ∠DBA = ∠DCA = 50°
In ∆OAC, OA = OC (Radii of the circle)
∴ ∠OAC = ∠OCA = ∠DCA = 50°
and ∠OAC + ∠OCA + ∠AOC = 180° (Sum of angles of a triangle)
⇒ 50° + 50° + ∠AOC = 180°
⇒ 100° + ∠AOC = 180°
⇒ ∠AOC = 180° – 100° = 80°
Hence ∠AOC = 80°

Question 8.
On a semi circle with AB as diameter, a point C is taken so that m (∠CAB) = 30°. Find m (∠ACB) and m (∠ABC).
Solution:
A semicircle with AB as diameter

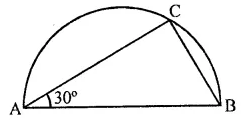
∠ CAB = 30°
∠ACB = 90° (Angle in a semi circle)
But ∠CAB + ∠ACB + ∠ABC = 180°
⇒ 30° + 90° + ∠ABC – 180°
⇒ 120° + ∠ABC = 180°
∴ ∠ABC = 180°- 120° = 60°
Hence m ∠ACB = 90°
and m ∠ABC = 60°

Question 9.
In a cyclic quadrilateral ABCD, if AB || CD and ∠B = 70°, find the remaining angles.
Solution:
In a cyclic quadrilateral ABCD, AB || CD and ∠B = 70°

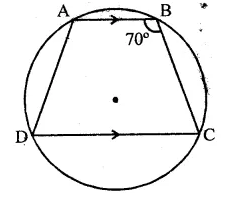
∵ ABCD is a cyclic quadrilateral
∴ ∠B + ∠D = 180°
⇒ 70° + ∠D = 180°
⇒ ∠D = 180°-70° = 110°
∵ AB || CD
∴ ∠A + ∠D = 180° (Sum of cointerior angles)
∠A+ 110°= 180°
⇒ ∠A= 180°- 110° = 70°
Similarly, ∠B + ∠C = 180°
⇒ 70° + ∠C- 180° ‘
⇒ ∠C = 180°-70°= 110°
∴ ∠A = 70°, ∠C = 110°, ∠D = 110°

Question 10.
In a cyclic quadrilateral ABCD, if m ∠A = 3(m ∠C). Find m ∠A.
Solution:
In cyclic quadrilateral ABCD, m ∠A = 3(m ∠C)

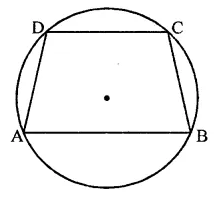
∵ ABCD is a cyclic quadrilateral,
∴ ∠A + ∠C = 180°
⇒ 3 ∠C + ∠C = 180° ⇒ 4∠C = 180°
⇒ ∠C = \(\frac { { 180 }^{ \circ } }{ 4 }\)  = 45°
∴ ∠A = 3 x 45°= 135°
Hence m ∠A =135°

Question 11.
In the figure, O is the centre of the circle and ∠DAB = 50°. Calculate the values of x and y.

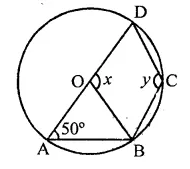
Solution:
In the figure, O is the centre of the circle ∠DAB = 50°
∵ ABCD is a cyclic quadrilateral
∴ ∠A + ∠C = 180°
⇒ 50° + y = 180°
⇒ y = 180° – 50° = 130°
In ∆OAB, OA = OB (Radii of the circle)
∴ ∠A = ∠OBA = 50°
∴ Ext. ∠DOB = ∠A + ∠OBA
x = 50° + 50° = 100°
∴ x= 100°, y= 130°

Question 12.
In the figure, if ∠BAC = 60° and ∠BCA = 20°, find ∠ADC.

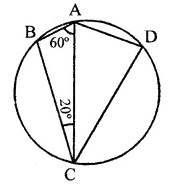
Solution:
In ∆ABC,
∠BAC + ∠ABC + ∠ACB = 180° (Sum of angles of a triangle)

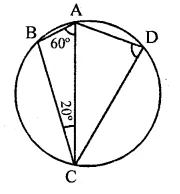
60° + ∠ABC + 20° = 180°
∠ABC + 80° = 180°
∴ ∠ABC = 180° -80°= 100°
∵ ABCD is a cyclic quadrilateral,
∴ ∠ABC + ∠ADC = 180°
100° + ∠ADC = 180°
∴ ∠ADC = 180°- 100° = 80°

Question 13.
In the figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC.

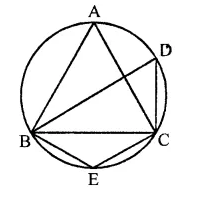
Solution:
In a circle, ∆ABC is an equilateral triangle

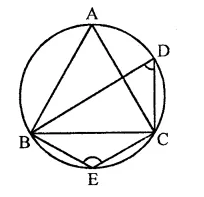
∴ ∠A = 60°
∵ ∠BAC and ∠BDC are in the same segment
∴ ∠BAC = ∠BDC = 60°
∵ BECD is a cyclic quadrilateral
∴ ∠BDC + ∠BEC = 180°
⇒ 60° + ∠BEC = 180°
⇒ ∠BEC = 180°-60°= 120°
Hence ∠BDC = 60° and ∠BEC = 120°

Question 14.
In the figure, O is the centre of the circle. If ∠CEA = 30°, find the values of x, y and z.

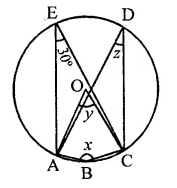
Solution:
∠AEC and ∠ADC are in the same segment
∴ ∠AEC = ∠ADC = 30°
∴ z = 30°
ABCD is a cyclic quadrilateral
∴ ∠B + ∠D = 180°
⇒ x + z = 180°
⇒ x + 30° = 180°
⇒ x = 180° – 30° = 150°
Arc AC subtends ∠AOB at the centre and ∠ADC at the remaining part of the circle
∴ ∠AOC = 2∠D = 2 x 30° = 60°
∴ y = 60°
Hence x = 150°, y – 60° and z = 30°

Question 15.
In the figure, ∠BAD = 78°, ∠DCF = x° and ∠DEF = y°. Find the values of x and y.

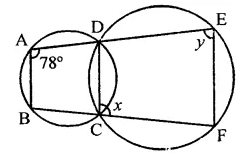
Solution:
In the figure, two circles intersect each other at C and D
∠BAD = 78°, ∠DCF = x, ∠DEF = y
ABCD is a cyclic quadrilateral
∴ Ext. ∠DCF = its interior opposite ∠BAD
⇒ x = 78°
In cyclic quadrilateral CDEF,
∠DCF + ∠DEF = 180°
⇒ 78° + y = 180°
⇒ y = 180° – 78°
y = 102°
Hence x = 78°, and y- 102°

Question 16.
In a cyclic quadrilateral ABCD, if ∠A – ∠C = 60°, prove that the smaller of two is 60°.
Solution:
In cyclic quadrilateral ABCD,
∠A – ∠C = 60°
But ∠A + ∠C = 180° (Sum of opposite angles)

Adding, 2∠A = 240° ⇒ ∠A = \(\frac { { 62 }^{ \circ } }{ 2 }\)  = 120° and subtracting
2∠C = 120° ⇒ ∠C = \(\frac { { 120 }^{ \circ } }{ 2 }\)  = 60°
∴ Smaller angle of the two is 60°.

Question 17.
In the figure, ABCD is a cyclic quadrilateral. Find the value of x.

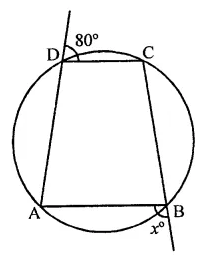
Solution:
∠CDE + ∠CDA = 180° (Linear pair)
⇒ 80° + ∠CDA = 180°
⇒ ∠CDA = 180° – 80° = 100°

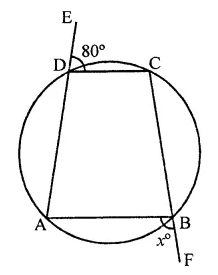
In cyclic quadrilateral ABCD,
Ext. ∠ABF = Its interior opposite angle ∠CDA = 100°
∴ x = 100°

Question 18.
ABCD is a cyclic quadrilateral in which:
(i) BC || AD, ∠ADC =110° and ∠B AC = 50°. Find ∠DAC.
(ii) ∠DBC = 80° and ∠BAC = 40°. Find ∠BCD.
(iii) ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.
Solution:
(i) In the figure,

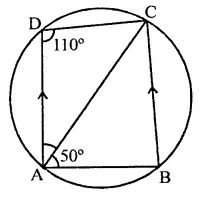
ABCD is a cyclic quadrilateral and AD || BC, ∠ADC = 110°
∠BAC = 50°
∵ ∠B + ∠D = 180° (Sum of opposite angles)
⇒ ∠B + 110° = 180°
∴ ∠B = 180°- 110° = 70°
Now in ∆ABC,
∠CAB + ∠ABC + ∠BCA = 180° (Sum of angles of a triangle)
⇒ 50° + 70° + ∠BCA = 180°
⇒ 120° + ∠BCA = 180°
⇒ ∠BCA = 180° – 120° = 60°
But ∠DAC = ∠BCA (Alternate angles)
∴ ∠DAC = 60°
(ii) In cyclic quadrilateral ABCD,
Diagonals AC and BD are joined ∠DBC = 80°, ∠BAC = 40°

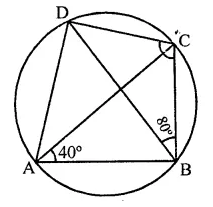
Arc DC subtends ∠DBC and ∠DAC in the same segment
∴ ∠DBC = ∠DAC = 80°
∴ ∠DAB = ∠DAC + ∠CAB = 80° + 40° = 120°
But ∠DAC + ∠BCD = 180° (Sum of opposite angles of a cyclic quad.)
⇒ 120° +∠BCD = 180°
⇒ ∠BCD = 180°- 120° = 60°
(iii) In the figure, ABCD is a cyclic quadrilateral BD is joined
∠BCD = 100°
and ∠ABD = 70°

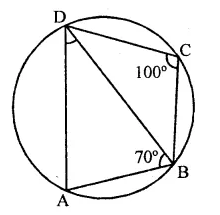
∠A + ∠C = 180° (Sum of opposite angles of cyclic quad.)
∠A+ 100°= 180°
⇒ ∠A= 180°- 100°
∴ ∠A = 80°
Now in ∆ABD,
∠A + ∠ABD + ∠ADB = 180° (Sum of angles of a triangle)
⇒ 80° + 70° + ∠ADB = 180°
⇒ 150° +∠ADB = 180°
⇒ ∠ADB = 180°- 150° = 30°
∴ ∠ADB = 30°

Question 19.
Prove that the circles described on the four sides of a rhombus as diameter, pass through the point of intersection of its diagonals.
Solution:
Given : ABCD is a rhombus. Four circles are drawn on the sides AB, BC, CD and DA respectively

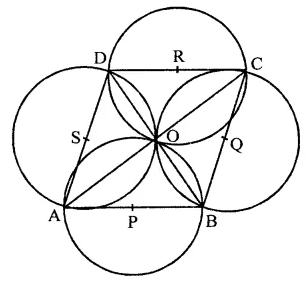
To prove : The circles pass through the point of intersection of the diagonals of the rhombus ABCD
Proof: ABCD is a rhombus whose diagonals AC and BD intersect each other at O
∵ The diagonals of a rhombus bisect each other at right angles
∴ ∠AOB = ∠BOC = ∠COD = ∠DOA = 90°
Now when ∠AOB = 90°
and a circle described on AB as diameter will pass through O
Similarly, the circles on BC, CD and DA as diameter, will also pass through O

Question 20.
If the two sides of a pair of opposite sides of a cyclic quadrilateral are equal, prove that is diagonals are equal.
Solution:
Given : In cyclic quadrilateral ABCD, AB = CD
AC and BD are the diagonals

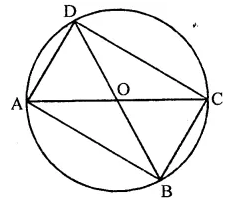
To prove : AC = BC
Proof: ∵ AB = CD
∴ arc AB = arc CD
Adding arc BC to both sides, then arc AB + arc BC = arc BC + arc CD
⇒ arc AC = arc BD
∴ AC = BD
Hence diagonal of the cyclic quadrilateral are equal.

Question 21.
Circles are described on the sides of a triangle as diameters. Prove that the circles on any two sides intersect each other on the third side (or third side produced).
Solution:
Given : In ∆ABC, circles are drawn on sides AB and AC
To prove : Circles drawn on AB and AC intersect at D which lies on BC, the third side
Construction : Draw AD ⊥ BC

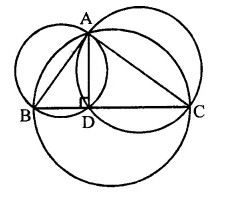
Proof: ∵ AD ⊥ BC
∴ ∠ADB = ∠ADC = 90°
So, the circles drawn on sides AB and AC as diameter will pass through D
Hence circles drawn on two sides of a triangle pass through D, which lies on the third side.

Question 22.
ABCD is a cyclic trapezium with AD || BC. If ∠B = 70°, determine other three angles of the trapezium.
Solution:
In the figure, ABCD is a trapezium in which AD || BC and ∠B = 70°

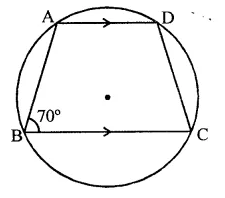
∵ AD || BC
∴ ∠A + ∠B = 180° (Sum of cointerior angles)
⇒ ∠A + 70° = 180°
⇒ ∠A= 180°- 70° = 110°
∴ ∠A = 110°
But ∠A + ∠C = 180° and ∠B + ∠D = 180° (Sum of opposite angles of a cyclic quadrilateral)
∴ 110° + ∠C = 180°
⇒ ∠C = 180°- 110° = 70°
and 70° + ∠D = 180°
⇒ ∠D = 180° – 70° = 110°
∴ ∠A = 110°, ∠C = 70° and ∠D = 110°

Question 23.
In the figure, ABCD is a cyclic quadrilateral in which AC and BD are its diagonals. If ∠DBC = 55° and ∠BAC = 45°, find ∠BCD.

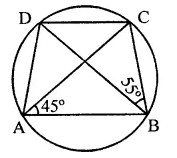
Solution:
In the figure, ABCD is a cyclic quadrilateral whose diagonals AC and BD are drawn ∠DBC = 55° and ∠BAC = 45°

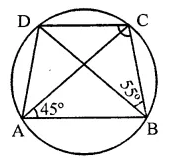
∵ ∠BAC and ∠BDC are in the same segment
∴ ∠BAC = ∠BDC = 45°
Now in ABCD,
∠DBC + ∠BDC + ∠BCD = 180° (Sum of angles of a triangle)
⇒ 55° + 45° + ∠BCD = 180°
⇒ 100° + ∠BCD = 180°
⇒ ∠BCD = 180° – 100° = 80°
Hence ∠BCD = 80°

Question 24.
Prove that the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent.
Solution:
Given : ABCD is a cyclic quadrilateral

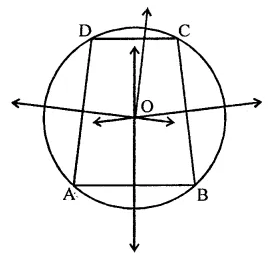
To prove : The perpendicular bisectors of the sides are concurrent
Proof : ∵ Each side of the cyclic quadrilateral is a chord of the circle and perpendicular of a chord passes through the centre of the circle
Hence the perpendicular bisectors of each side will pass through the centre O
Hence the perpendicular bisectors of the sides of a cyclic quadrilateral are concurrent

Question 25.
Prove that the centre of the circle circumscribing the cyclic rectangle ABCD is the point of intersection of its diagonals.
Solution:
Given : ABCD is a cyclic rectangle and diagonals AC and BD intersect each other at O

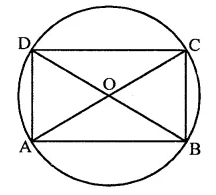
To prove : O is the point of intersection is the centre of the circle.
Proof : Let O be the centre of the circle- circumscribing the rectangle ABCD
Since each angle of a rectangle is a right angle and AC is the chord of the circle
∴ AC will be the diameter of the circle Similarly, we can prove that diagonal BD is also the diameter of the circle
∴ The diameters of the circle pass through the centre
Hence the point of intersection of the diagonals of the rectangle is the centre of the circle.

Question 26.
ABCD is a cyclic quadrilateral in which BA and CD when produced meet in E and EA = ED. Prove that:
(i) AD || BC
(ii) EB = EC.
Solution:
Given : ABCD is a cyclic quadrilateral in which sides BA and CD are produced to meet at E and EA = ED

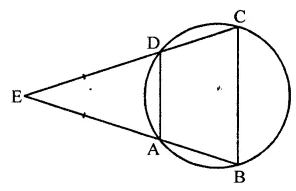
To prove :
(i) AD || BC
(ii) EB = EC
Proof: ∵ EA = ED
∴ In ∆EAD
∠EAD = ∠EDA (Angles opposite to equal sides)
In a cyclic quadrilateral ABCD,
Ext. ∠EAD = ∠C
Similarly Ext. ∠EDA = ∠B
∵ ∠EAD = ∠EDA
∴ ∠B = ∠C
Now in ∆EBC,
∵ ∠B = ∠C
∴ EC = EB (Sides opposite to equal sides)
and ∠EAD = ∠B
But these are corresponding angles
∴ AD || BC

Question 27.
Prove that the angle in a segment shorter than a semicircle is greater than a right angle.
Solution:
Given : A segment ACB shorter than a semicircle and an angle ∠ACB inscribed in it
To prove : ∠ACB < 90°
Construction : Join OA and OB

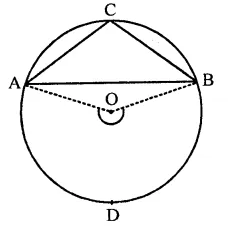
Proof : Arc ADB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle ∴ ∠ACB = \(\frac { 1 }{ 2 }\) ∠AOB But ∠AOB > 180° (Reflex angle)
∴ ∠ACB > \(\frac { 1 }{ 2 }\) x [80°
⇒ ∠ACB > 90°

Question 28.
Prove that the angle in a segment greater than a semi-circle is less than a right angle
Solution:
Given : A segment ACB, greater than a semicircle with centre O and ∠ACB is described in it
To prove : ∠ACB < 90°
Construction : Join OA and OB

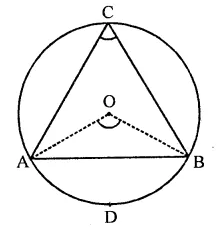
Proof : Arc ADB subtends ∠AOB at the centre and ∠ACB at the remaining part of the circle
∴ ∠ACB =\(\frac { 1 }{ 2 }\) ∠AOB
But ∠AOB < 180° (A straight angle) 1
∴ ∠ACB < \(\frac { 1 }{ 2 }\) x 180°
⇒ ∠ACB <90°
Hence ∠ACB < 90°

Question 29.
Prove that the line segment joining the mid-point of the hypotenuse of a rijght triangle to its opposite vertex is half of the hypotenuse.
Solution:
Given : In a right angled ∆ABC
∠B = 90°, D is the mid point of hypotenuse AC. DB is joined.
To prove : BD = \(\frac { 1 }{ 2 }\) AC
Construction : Draw a circle with centre D and AC as diameter

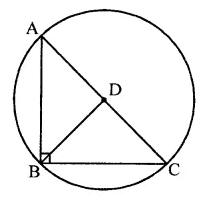
Proof: ∵ ∠ABC = 90°
∴ The circle drawn on AC as diameter will pass through B
∴ BD is the radius of the circle
But AC is the diameter of the circle and D is mid point of AC
∴ AD = DC = BD
∴ BD= \(\frac { 1 }{ 2 }\) AC

Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.