RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
Other Exercises
- RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.1
- RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.2
- RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.3
- RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.4
- RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles Ex 15.5
- RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS
- RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles MCQS
Question 1.
In the figure, two circles intersect at A and B. The centre of the smaller circle is O and it lies on the circumference of the larger circle. If ∠APB = 70°, find ∠ACB.
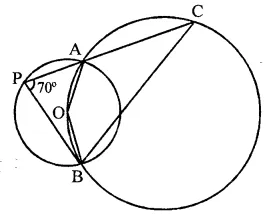
Solution:
Arc AB subtends ∠AOB at the centre and ∠APB at the remaining part of the circle
∴ ∠AOB = 2∠APB = 2 x 70° = 140°
Now in cyclic quadrilateral AOBC,
∠AOB + ∠ACB = 180° (Sum of the angles)
⇒ 140° +∠ACB = 180°
⇒ ∠ACB = 180° – 140° = 40°
∴ ∠ACB = 40°
Question 2.
In the figure, two congruent circles with centre O and O’ intersect at A and B. If ∠AO’B = 50°, then find ∠APB.
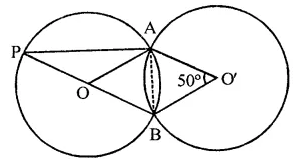
Solution:
Two congruent circles with centres O and O’ intersect at A and B
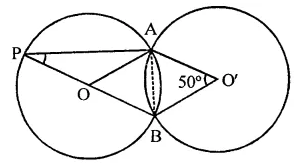
∠AO’B = 50°
∵ OA = OB = O’A = 04B (Radii of the congruent circles)

Question 3.
In the figure, ABCD is a cyclic quadrilateral in which ∠BAD = 75°, ∠ABD = 58° and ∠ADC = IT, AC and BD intersect at P. Then, find ∠DPC.
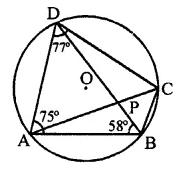
Solution:
∵ ABCD is a cyclic quadrilateral,
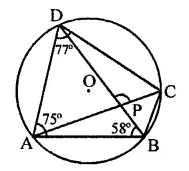
∴ ∠BAD + ∠BCD = 180°
⇒ 75° + ∠BCD – 180°
⇒ ∠BCD = 180°-75°= 105° and ∠ADC + ∠ABC = 180°
⇒ 77° + ∠ABC = 180°
⇒ ∠ABC = 180°-77°= 103°
∴ ∠DBC = ∠ABC – ∠ABD = 103° – 58° = 45°
∵ Arc AD subtends ∠ABD and ∠ACD in the same segment of the circle 3
∴ ∠ABD = ∠ACD = 58°
∴ ∠ACB = ∠BCD – ∠ACD = 105° – 58° = 47°
Now in ∆PBC,
Ext. ∠DPC = ∠PBC + ∠PCB
=∠DBC + ∠ACB = 45° + 47° = 92°
Hence ∠DPC = 92°
Question 4.
In the figure, if ∠AOB = 80° and ∠ABC = 30°, then find ∠CAO.
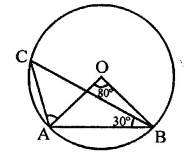
Solution:
In the figure, ∠AOB = 80°, ∠ABC = 30°
∵ Arc AB subtends ∠AOB at the centre and
∠ACB at the remaining part of the circle
∴ ∠ACB = \(\frac { 1 }{ 2 }\)∠AOB = \(\frac { 1 }{ 2 }\) x 80° = 40°
In ∆OAB, OA = OB
∴ ∠OAB = ∠OBA
But ∠OAB + ∠OBA + ∠AOB = 180°
∴ ∠OAB + ∠OBA + 80° = 180°
⇒ ∠OAB + ∠OAB = 180° – 80° = 100°
∴ 2∠OAB = 100°
⇒ ∠OAB = \(\frac { { 100 }^{ \circ } }{ 2 }\) = 50°
Similarly, in ∆ABC,
∠BAC + ∠ACB + ∠ABC = 180°
∠BAC + 40° + 30° = 180°
⇒ ∠BAC = 180°-30°-40°
= 180°-70°= 110°
∴ ∠CAO = ∠BAC – ∠OAB
= 110°-50° = 60°
Question 5.
In the figure, A is the centre of the circle. ABCD is a parallelogram and CDE is a straight line. Find ∠BCD : ∠ABE.
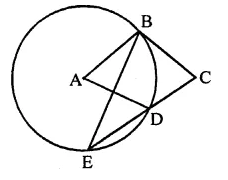
Solution:
In the figure, ABCD is a parallelogram and
CDE is a straight line
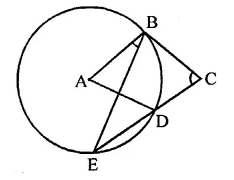
∵ ABCD is a ||gm
∴ ∠A = ∠C
and ∠C = ∠ADE (Corresponding angles)
⇒ ∠BCD = ∠ADE
Similarly, ∠ABE = ∠BED (Alternate angles)
∵ arc BD subtends ∠BAD at the centre and
∠BED at the remaining part of the circle
Question 6.
In the figure, AB is a diameter of the circle such that ∠A = 35° and ∠Q = 25°, find ∠PBR.
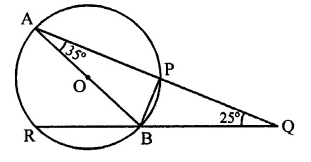
Solution:
In the figure, AB is the diameter of the circle such that ∠A = 35° and ∠Q = 25°, join OP.
Arc PB subtends ∠POB at the centre and
∠PAB at the remaining part of the circle
∴ ∠POB = 2∠PAB = 2 x 35° = 70°
Now in ∆OP,
OP = OB radii of the circle
∴ ∠OPB = ∠OBP = 70° (∵ ∠OPB + ∠OBP = 140°)
Now ∠APB = 90° (Angle in a semicircle)
∴ ∠BPQ = 90°
and in ∆PQB,
Ext. ∠PBR = ∠BPQ + ∠PQB
= 90° + 25°= 115°
∴ ∠PBR = 115°
Question 7.
In the figure, P and Q are centres of two circles intersecting at B and C. ACD is a straight line. Then, ∠BQD =
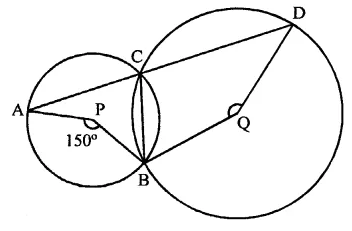
Solution:
In the figure, P and Q are the centres of two circles which intersect each other at C and B
ACD is a straight line ∠APB = 150°
Arc AB subtends ∠APB at the centre and
∠ACB at the remaining part of the circle
∴ ∠ACB = \(\frac { 1 }{ 2 }\) ∠APB = \(\frac { 1 }{ 2 }\) x 150° = 75°
But ∠ACB + ∠BCD = 180° (Linear pair)
⇒ 75° + ∠BCD = 180°
∠BCD = 180°-75°= 105°
Now arc BD subtends reflex ∠BQD at the centre and ∠BCD at the remaining part of the circle
Reflex ∠BQD = 2∠BCD = 2 x 105° = 210°
But ∠BQD + reflex ∠BQD = 360°
∴ ∠BQD+ 210° = 360°
∴ ∠BQD = 360° – 210° = 150°
Question 8.
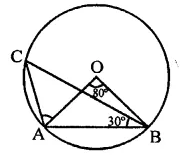
In the figure, if O is circumcentre of ∆ABC then find the value of ∠OBC + ∠BAC.
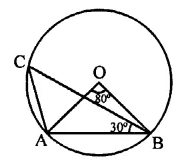
Solution:
In the figure, join OC
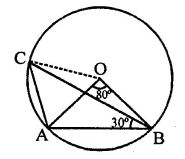
∵ O is the circumcentre of ∆ABC
∴ OA = OB = OC
∵ ∠CAO = 60° (Proved)
∴ ∆OAC is an equilateral triangle
∴ ∠AOC = 60°
Now, ∠BOC = ∠BOA + ∠AOC
= 80° + 60° = 140°
and in ∆OBC, OB = OC
∠OCB = ∠OBC
But ∠OCB + ∠OBC = 180° – ∠BOC
= 180°- 140° = 40°
⇒ ∠OBC + ∠OBC = 40°
∴ ∠OBC = \(\frac { { 40 }^{ \circ } }{ 2 }\) = 20°
∠BAC = OAB + ∠OAC = 50° + 60° = 110°
∴ ∠OBC + ∠BAC = 20° + 110° = 130°
Question 9.
In the AOC is a diameter of the circle and arc AXB = 1/2 arc BYC. Find ∠BOC.
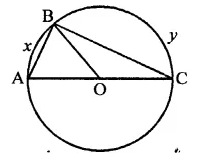
Solution:
In the figure, AOC is diameter arc AxB = \(\frac { 1 }{ 2 }\) arc BYC 1
∠AOB = \(\frac { 1 }{ 2 }\) ∠BOC
⇒ ∠BOC = 2∠AOB
But ∠AOB + ∠BOC = 180°
⇒ ∠AOB + 2∠AOB = 180°
⇒ 3 ∠AOB = 180°
∴ ∠AOB = \(\frac { { 180 }^{ \circ } }{ 3 }\) = 60°
∴ ∠BOC = 2 x 60° = 120°
Question 10.
In the figure, ABCD is a quadrilateral inscribed in a circle with centre O. CD produced to E such that ∠AED = 95° and ∠OBA = 30°. Find ∠OAC.
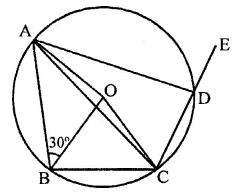
Solution:
In the figure, ABCD is a cyclic quadrilateral
CD is produced to E such that ∠ADE = 95°
O is the centre of the circle
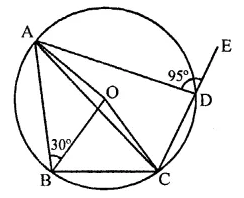
∵ ∠ADC + ∠ADE = 180°
⇒ ∠ADC + 95° = 180°
⇒ ∠ADC = 180°-95° = 85°
Now arc ABC subtends ∠AOC at the centre and ∠ADC at the remaining part of the circle
∵ ∠AOC = 2∠ADC = 2 x 85° = 170°
Now in ∆OAC,
∠OAC + ∠OCA + ∠AOC = 180° (Sum of angles of a triangle)
⇒ ∠OAC = ∠OCA (∵ OA = OC radii of circle)
∴ ∠OAC + ∠OAC + 170° = 180°
2∠OAC = 180°- 170°= 10°
∴ ∠OAC = \(\frac { { 10 }^{ \circ } }{ 2 }\) = 5°
Hope given RD Sharma Class 9 Solutions Chapter 15 Areas of Parallelograms and Triangles VSAQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.